Однородность магнитного поля системы круглых и квадратных проводников с током

Проблема получения высокооднородных магнитных полей интересна сама как сама по себе, так и для применения магнитных полей с целью калибровки большого количества технических устройств, для проведения различных физических и биофизических экспериментов. Простейшими системами для получения достаточно однородного постоянного или переменного магнитного поля с открытым доступом для образцов произвольной формы являются системы круглых и квадратных проводников с током. Однородность магнитных полей данных типов проводников вдоль оси симметрии была изучена в работах [6]. В данной статье мы сравниваем однородность магнитного поля во всем пространстве между проводниками.

Магнитное поле круглых и квадратных проводников с током

Следуя [1, 2], рассмотрим магнитное поле в цилиндрической системе координат (z, р, ф) двух соосных круглых проводников (рис. 1а) радиусом R, током I, на расстоянии 21 друг от друга в безразмерных переменных

Рис. 1. Система двух соосных эквивалентных круглых (а) и квадратных (б) проводников с током. Область расчета (в) - рабочая область системы квадратных проводников с током

X    Y    Z    ^Х2 + Y2    R     a x = -,y=-,z = -,p=-------,r = ?,d=-          (1)

(

B(z,p,r) = J

BZ (z, p, r) + B² (z, p, r) + B 2 (z, p, r)

B_z(z,p,r) = ^Ц F 2 ⁽z,p,r), 2m

Bp (z, p, r) =     T; (z, p, r), p          2n(

Bv = 0,

F ; (z,p,r) = F ;i (z,p,r) + F₂₂(z,p,r),     T₂(z, p,r) = T₂i(z, p,r) + T₂₂(z,p,r),

F ;i ⁽z, p,r)

К (m i ^(z, p,^r)) + (^r_{r  p}^p) 2 + ^<^⁺+1) 2 ^{E (m} i ^(z, p,^r)) ^(r + p)² + (z + 1)²

,   ,     " r2 _ p2 _ (z _ 1)2

^К(m 2 ^(z, p, ^r)) + (_{r  p}^P 2 + (_z  1) 2 ^£(m 2 ^(z, p, ^r))

V(r + p)2 + (z _ 1)2

T 21 ⁽z,p,r) =

z + 1

p

T 22 ⁽z,p,r) =

z _ 1

p

wr г     лл , r² + p² + (z + 1)²

^_K(m 1 ^(z,^p,^{r)) +} (r_p) 2 + (z+1) 2

7(r + p)2 + (z +1)2

+ ^r 2 ⁺ p^{2 + (z _ 1)2}

^K(m 2 ⁽Z, ^p,r)) + (r _ p)² + (z _ 1)²

V(r + p)2 + (z _ 1)2

F(m i (z, p, r))

,

F(m2(z, p,r))

,

0 < m 1 (z, p, r) =

4rp

(r + p)2 + (z + 1)2

< 1,0 < m2 (z, p, r) =

4rp

(r + p)2 + (z _ 1)2

< 1,

v

П

K(m) = J 0

dp

^1 _ msm23

П

F(m) = J V1 _ msm20 dp.

Здесь K(m) и F(m) _ эллиптические интегралы 1 и 2 рода. Для случая p = 0 имеем [16]

х    Р0^ ,          11

Bz (z, 0, r) = — r2--------------3 +

²    [r² + (z + 1)²] 2    [r² + (z _ 1)²] 2

Bp(0,0,r) = 0,Bz(0,0,r) = Bo(r) = ^y—r2----1

(r² + 1) 2

Пусть рабочая область определяется неравенствами

0 < p = V^2 + У2 < 1, _1 < z < 1.

Раскладывая проекции вектора магнитной индукции в ряд по пространственным переменным в центральной точке, потребуем, чтобы вторая производная равнялась нулю. Такие системы принято называть системами Гельмгольца. Равенство нулю производной соответствует значению r = r0 = 2.                                      (4)

Все нечетные производные равны нулю из-за симметрии системы [2]. Таким образом, разложение в ряд Тейлора начинается с производной 4 порядка (кроме нулевой).

Такую систему называют системой 4 порядка [3].

Следуя [18], рассмотрим магнитное поле в декартовой системе координат (%, у, z) двух соосных квадратных проводников

(рис. 1б) со стороной а, током I, на рас- переменных (1) стоянии 21 друг от друга в безразмерных

	B (x, y, z,d) = JB x (x, y, z, d) + B y (x, y, z, d) + B ^ (x, y, z, d'),
Bx(x,y,z, d) =	8 Ио^О = -7-; / B xi( x,y,z,d), 4П1 Z—i
Bx i( x,y,z,d)	(y+ d)(z — 1)
	[(x — d) 2 + (z — 1) 2 ]^(x — d) 2 + (y + d)2 + (z — 1) 2
BX 2( x,y,z,d)	(y + d)(z — 1)
	[(x + d)2 + (z — 1) 2 ]V(x + d)2 + (y + d)2 + (z — 1) 2 ,
BX 3( x,y,z,d)	(y — d)(z — 1)
	[(x + d) 2 + (z — 1) 2 ]V(x + d) 2 + (y — d)2 + (z — 1) 2
B x4( x,y,z,d)	(y — d)(z — 1)
	[(x — d)2 + (z — 1)2]V(x — d)2 + (y — d)2 + (z — 1) 2 ,
B xs( x,y,z,d)	(y+ d)(z+ 1)
	[(x — d) 2 + (z + 1) 2 ]V(x — d) 2 + (y + d)2 + (z+ 1) 2
B x 6 ( x,y,z,d)	(y + d)(z + 1)
	[(x + d)2 + (z + 1) 2 ]V(x + d)2 + (y + d)2 + (z + 1) 2 ,
B x7( x,y,z,d)	(y — d)(z+ 1)
	[(x + d) 2 + (z + 1) 2 ]V(x + d) 2 + (y — d) 2 + (z + 1) 2
B x 8 ( x,y,z,d)	(y — d)(z + 1)
	[(x — d) 2 + (z + 1) 2 ]^(x — d) 2 + (y — d) 2 + (z + 1) 2
By(x,y,z,d) =	= -7-; / B y i(x,y,z,d), 4nl
By i (x,y, z,d)	i-1 (x + d)(z — 1)
	[(y — d) 2 + (z — 1) 2 ]V(x + d) 2 + (y — d) 2 + (z — 1) 2 ,
B y2 (x,y, z, d)	(x + d)(z — 1)
	[(y + d) 2 + (z — 1) 2 ]7(x + d) 2 + (y + d) 2 + (z — 1) 2 ,
By3(x,y, z, d)	(x — d)(z — 1)
	—
	[(y + d) 2 + (z — 1) 2 ]^(x — d) 2 + ((y + d) 2 + (z — 1) 2
B y4 (x,y, z,d)	(x — d)(z — 1)
	[(y — d) 2 + (z — 1) 2 ]V(x — d) 2 + (y — d) 2 + (z — 1) 2 ,
B y 5(x,y, z, d)	(x + d)(z + 1)
	=---------------------------- .
	[(y — d) 2 + (z + 1) 2 ]^(x + d) 2 + (y — d) 2 + (z + 1) 2
B y 6(x,y, z,d)	(x + d)(z + 1)
	,
	[(y + d) 2 + (z + 1) 2 ]V(x + d) 2 + (y + d) 2 + (z + 1) 2
B y7 (x,y, z, d)	(x — d)(z + 1)
	—— ____________________________________________________________________________
	[(y + d) 2 + (z + 1) 2 ]V(x — d) 2 + (y + d) 2 + (z + 1) 2 ,
B y 8(x,y, z,d)	(x — d)(z + 1)
	[(y — d) 2 + (z + 1) 2 ]V(x — d) 2 + (y — d) 2 + (z + 1) 2 ,

B_z(x,y,z,d) = -°- >  B_zi ⁽ x,y,z,d), 4nl i=i

Bzl(x,y,z,d) = B z2 (x,y,z,d) = Bz3 (x, y, z, d) = B z4 (x,y,z,d) = Bz5(x, y,z, d) = B z6 (x,y,z,d) = Bz7(x, y,z, d) = B z8 (x,y,z,d) = B z9 (x,y,z,d) = B zio (x,y,z,d) = B zii (x,y,z,d) = B zi2 (x, y, z, d) = B zi3 (x, y, z, d) = Bz14(x,y,z,d) = B zi5 (x,y,z,d) = B zi6 (x,y,z,d) = Для случаяx	(x + d)(y + d)
	[(y + d)2 + (z - 1)2]V(x + d)2 + (y + d)2 + (z - 1)2, (x + d)(y + d)
	[(x + d)2 + (z — 1)2]^(x + d)2 + (y + d)2 + (z — 1)2 (x + d)(y — d)
	[(y — d)2 + (z — 1)2]V(x + d)2 + (y — d)2 + (z — 1)2, (x + d)(y — d)
	[(x + d)2 + (z — 1)2]^(x + d)2 + (y — d)2 + (z — 1)2 (x — d)(y + d)
	[(x — d)2 + (z — 1)2]V(x — d)2 + (y + d)2 + (z — 1)2, (x — d)(y + d)
	[(y + d)2 + (z — 1)2]^(x — d)2 + (y + d)2 + (z — 1)2 (x — d)(y — d)
	[(x — d)2 + (z — 1)2]V(x + d)2 + (y — d)2 + (z — 1)2, (x —d)(y — d)
	[(y — d)2 + (z — 1)2]^(x — d)2 + (y — d)2 + (z — 1)2 (x + d)(y + d)
	[(y + d)2 + (z + 1)2]V(x + d)2 + (y + d)2 + (z + 1)2, (x + d)(y + d)
	[(x + d)2 + (z + 1)2]V(x + d)2 + (y + d)2 + (z + 1)2, (x + d)(y —d)
	[(y — d)2 + (z + 1)2]V(x + d)2 + (y — d)2 + (z + 1)2, (x + d)(y — d)
	[(x + d)2 + (z + 1)2]V(x + d)2 + (y — d)2 + (z + 1)2, (x —d)(y + d)
	[(x — d)2 + (z + 1)2]V(x — d)2 + (y + d)2 + (z + 1)2, (x — d)(y + d)
	[(y + d)2 + (z + 1)2]V(x — d)2 + (y + d)2 + (z + 1)2, (x —d)(y —d)
	[(x — d)2 + (z + 1)2]^(x + d)2 + (y — d)2 + (z + 1)2 (x — d)(y — d)
	[(y — d)2 + (z + 1)2]V(x — d)2 + (y — d)2 + (z + 1)2 : = y = 0 [18, 19] имеем Bz(0,0,z,d) = — ^d2 1 1 ,          ---
	n ^   I((z + 1)2 + d2)V(z + 1)2 + 2d2

+---------------1              ],

((z - 1)2 + d2)7(z-1)2 + 2d2J

4-,/

B_x(0,0,0,d) = B_y(0,0,0,d) = 0,B z (0,0,0,d) = B o (d) = — -- TT / /

d2

Пусть рабочая область определяется неравенствами

-1 < х < 1,-1 < у < 1,-1 < z < 1.

Раскладывая проекции вектора магнитной индукции в ряд по пространственным переменным в центральной точке, потребуем, чтобы вторая производная равнялась нулю. Это приводит к кубическому уравнению [5, 6], решением которого является значение

d = di0~ 1.837.

Все нечетные производные равны нулю из-за симметрии системы. Таким образом, разложение в ряд Тейлора начинается с производной 4 порядка (кроме нулевой), и эта система также является системой 4 по рядка.

Сравнение неоднородности магнитных полей систем проводников с током

, ,             B(z,7%2 +у2,го)

^c(x,y,z)   1         50 (Г0)       ,

Чем меньше модуль значения h(x, у, z), тем более однородным является магнитное поле. Полностью однородное магнитное поле имеет значение h = 0 во всей области пространства. Если h(x, у, z) > 0, то модуль вектора магнитной индукции в данной точке пространства меньше, чем в центральной     х = у = z = 0.     Если

Введем коэффициент неоднородности магнитного поля, сравнивая его значение в произвольной точке со значением в центре системы. Расчеты показывают, что проекции 5_Х и 5_у малы. Поэтому магнитное поле с большой точностью направлено вдоль оси z. Для круглых (c) и квадратных (s) проводников имеем, соответственно, выражения:

_      ч        5(х, у,z, d0)

hs(x,y,z) = 1--°<       (8)

50(“o)

h(х,у,z) < 0 — то больше. Будем сравнивать магнитные поля в рабочей области системы квадратных проводников с током. Область 1: -1 < х < 1,-1 < у < 1,z = 0; область 2: -1 < х < 1,у = 0, -1 < z < 1; область 3: -1 < х < 1, -1 < у < 1, z = 1.

а

б

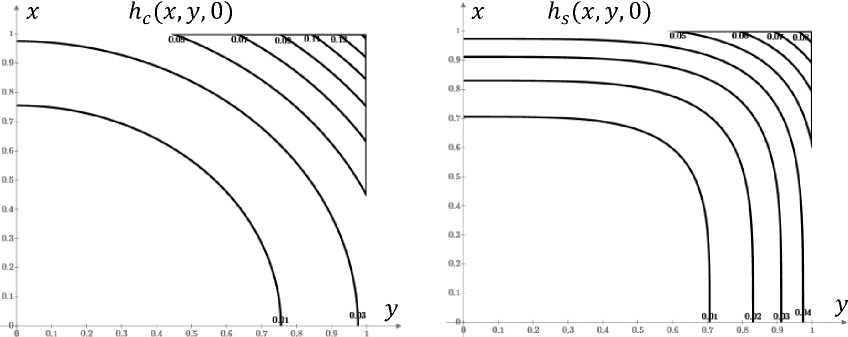
Рис. 2. Изолинии одинаковых значений коэффициента неоднородности в области 1 (z = 0): а - система круглых проводников с током, б - система квадратных проводников с током. Показана четвертая часть области.

На рисунке 2 построенные изолинии значений коэффициентов неоднородности располагаются или в виде концентрических окружностей (круглые проводники), или в виде концентрических овалов (квадратные проводники) вокруг центральной точки области х = 0,у = 0,z = 0, где коэффициенты неоднородности равны нулю. С увеличением расстояния до центра коэффициенты неоднородности растут (однородность падает) приблизительно одинаковым образом, изменяясь для круглых и квадратных проводников от значения ^_с(0,0,0) = й₅(0,0,0) = 0 до значений ^_с(1,1,0) = 0.156 и h₅(1,1,0) = 0.087, соответственно.

Пространственные распределения коэффициентов неоднородности (рис. 3) для обоих типов проводников с током имеют достаточно похожий вид. Неоднородность растет как по мере удаления вдоль оси z от нулевого значения, так и по мере удаления от нулевого значения вдоль оси х. При этом для всех х > 0 существует значение z ^ 0, где магнитное поле совпадает с центральным, т.е. кривая пересекает ось z. Для z = 1 в обоих случаях это имеет место для х ~ 0.7.

На рисунке 4 построенные изолинии значений коэффициентов неоднородности располагаются (также как и на рисунке 2) или в виде концентрических окружностей (круглые проводники) или в виде концентрических овалов (квадратные проводники) вокруг центральной точки области х = 0,у = 0, z = 1. Однако коэффициенты неоднородности равны нулю приблизительно в точках с координатами х² + у² ~ 0.7 2 , z = 1, а не в центральной точке, что соответствует рисунку 3. С увеличением расстояния до указанной выше кривой модули коэффициентов неоднородности растут (однородность падает) приблизительно одинаковым образом, изменяясь для круглых и квадратных проводников от значения h_c(0,0,1) = 0.054 и й₅(0,0,1) = 0.054, через ноль до значений й_с(1,1,1) = -0.380 и й₅(1,1,1) = -0.246, соответственно.

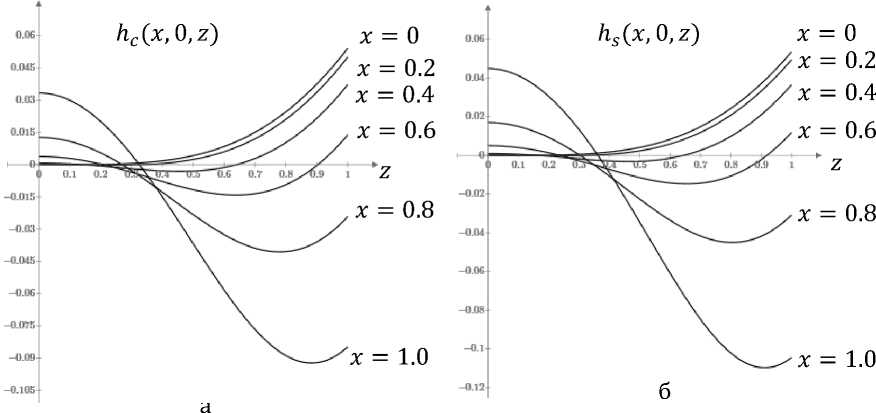
Рис. 3 Пространственное распределение коэффициента неоднородности вдоль оси z для разных значений х (область 2): а - система круглых проводников с током, б - система квадратных проводников с током. Показана четвертая часть области.

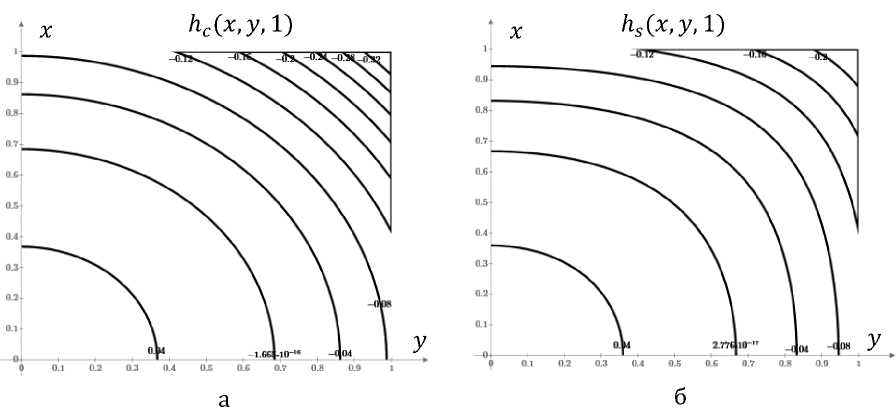
Рис. 4. Изолинии одинаковых значений коэффициента неоднородности в области 3 (z = 1): а - система круглых проводников с током, б - система квадратных проводников с током. Показана четвертая часть области.

Заключение

Таким образом, однородности магнитных полей круглых и квадратных систем проводников с током приблизительно одинаковы в пространстве между ними. При этом магнитное поле наиболее одно- z = 0. В этих областях неоднородность составляет порядка 0.01. Для получения более однородных полей необходимо использовать системы проводников с током с большим числом проводников.

родно как вдоль оси z, так и в плоскости