Одновременное управление движением центра масс и вокруг центра масс при маневрах космических аппаратов на геостационарной и высокоэллиптических орбитах c использованием электрореактивных двигателей
Автор: Платонов Валерий Николаевич
Журнал: Космическая техника и технологии @ktt-energia
Статья в выпуске: 1 (1), 2013 года.
Бесплатный доступ
Разработаны алгоритмы управления накопленным кинетическим моментом инерционных исполнительных органов космических аппаратов (КА) при проведении маневров с использованием электрореактивных двигателей, расположенных по схеме, обеспечивающей одновременное создание сил и управляющих моментов относительно центра масс КА. Приведены результаты летно-конструкторских испытаний геостационарного КА «Ямал-202» и математического моделирования маневров перспективного КА на высокоэллиптической орбите.
Маневр, электрореактивные двигатели, инерционные исполнительные органы
Короткий адрес: https://sciup.org/14343407
IDR: 14343407 | УДК: 629.78.05:521.322:621.452
Текст научной статьи Одновременное управление движением центра масс и вокруг центра масс при маневрах космических аппаратов на геостационарной и высокоэллиптических орбитах c использованием электрореактивных двигателей
В системах управления движением (СУД) современных космических аппаратов (КА) для проведения маневров широко используются электрореактивные двигатели (ЭРД). Удельный импульс тяги ЭРД в несколько раз превышает аналогичный показатель жидкостных реактивных двигателей. Поэтому использование ЭРД позволяет значительно сократить расход топлива на проведение коррекций орбиты.
ЭРД, используемые в современных отечественных СУД, имеют тягу 0,04 или 0,085 Н. При этом они ограничены по количеству включений (2 500...5 000) и ресурсу работы (2 000...2 500 ч).
Для автоматических КА коррекции орбиты проводятся как в трансверсальном, так и боковом направлениях. Для обеспечения коррекций орбиты в данных направлениях необходимо не менее четырех ЭРД. С учетом ограничений по ресурсу работы, количеству включений, резервированию и обеспечению работы КА в течение 10...18 лет количество ЭРД в системе управления движением КА должно быть увеличено до восьми. Далее в тексте вместо ЭРД используется название тяговый модуль (ТМ).
В СУД автоматических КА, разрабатываемых в РКК «Энергия», на геостационарной и высокоэллиптической орбитах (ВЭО) используется система, в составе которой восемь двигателей ТМ, при этом каждый модуль создает управляющий момент вокруг центра масс. Переключением отдельных ТМ в процессе коррекции орбиты можно обеспечить решение следующих задач:
-
• исключение расхода топлива на стабилизацию при коррекциях орбиты с использованием ТМ и системы маховиков за счет одновременного управления движением центра масс и вокруг него;
-
• сокращение расхода топлива на разгрузку накопленного кинетического момента маховиков между коррекциями орбиты за счет частичного или полного сброса вышеуказанного момента во время проведения коррекций орбиты.
Управление кинетическим моментом при маневрах спутников связи серии «Ямал»
При маневрах геостационарных спутников связи «Ямал» используется система из восьми ТМ с номинальной тягой каждого модуля 0,04 Н. Для управления ориентацией применяются инерционные исполнительные органы (ИИО): четыре маховика с кинетическим моментом 18 Н.м.с каждый. Оси вращения трех маховиков параллельны связанным осям КА, а находящегося в холодном резерве четвертого — параллельна биссектрисе трехгранного угла, образованного связанными осями. В случае штатной работы маховиков область вариации кинетического момента ИИО, обозначаемая через S, имеет форму куба.
Из-за ограничений по энергопотреблению во время штатной работы КА возможна одновременная работа только одного ТМ.
Для пояснения схемы расположения ТМ введем следующие системы координат с началом в центре масс КА:
-
• орбитальную систему координат (ОСК) 0 X 0 Y 0 Z 0 (ось 0 X 0 направлена от центра масс КА к центру Земли, 0 Z 0 противоположна вектору орбитальной угловой скорости КА, ось 0 Y 0 находится в плоскости орбиты и образует острый угол с направлением вектора линейной скорости КА);
-
• связанную систему координат 0 XYZ , направления осей которой определены в конструкторской документации КА.
При поддержании орбитальной ориентации оси связанной системы координат 0 XYZ совпадают с соответствующими осями ОСК 0 X 0 Y 0 Z 0 .
Восемь ТМ поровну распределены на два пояса, которые находятся в плоскостях, параллельных плоскости 0 YZ, и расположены по разные стороны от центра масс (схема размещения ТМ представлена на рис. 1). Расстояние между поясами, равное 0,16 м, позволяет создать управляющие моменты каждым ТМ вокруг осей 0 Y , 0 Z с учетом смещения центра масс при полете КА из-за выработки топлива и перекосов в направлениях векторов тяг ТМ. Плечи тяг ТМ относительно оси 0 X равны 0,3 м.
Тяговые модули расположены на ребрах КА (для исключения влияния струй двигателей на приемопередающие антенны и панели солнечных батарей), векторы тяг — под углом 42,5° к оси 0 Z . Векторы тяг имеют большую проекцию на ось 0 Z , чем на 0 Y , поскольку частота проведения коррекций орбиты по наклонению (по оси 0 Z ) выше, чем по трансверсали (по оси 0 Y ).
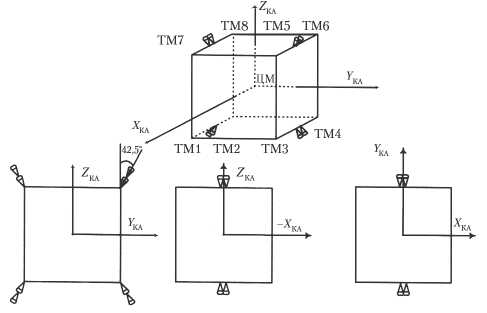
Рис. 1. Схема размещения восьми ТМ
В таблице приведены номинальные значения сил и моментов каждого из восьми ТМ для КА на геостационарной орбите.
Силы и моменты ТМ КА серии «Ямал»:
P 1 = 0,0265 Н; P 2 = 0,0289 H; M 1 = 0,01183 Н . м;
M 2 = 0,00237 Н . м; M 3 = 0,00217 Н . м
|
Тяговый модуль |
FY |
FZ |
MX |
MY |
MZ |
|
ТМ1 |
P 1 |
P 2 |
– M 1 |
– M 2 |
M 3 |
|
ТМ2 |
P 1 |
P 2 |
– M 1 |
M 2 |
– M 3 |
|
ТМ3 |
– P 1 |
P 2 |
M 1 |
– M 2 |
– M 3 |
|
ТМ4 |
– P 1 |
P 2 |
M 1 |
M 2 |
M 3 |
|
ТМ5 |
– P 1 |
– P 2 |
– M 1 |
M 2 |
– M 3 |
|
ТМ6 |
– P 1 |
– P 2 |
– M 1 |
– M 2 |
M 3 |
|
ТМ7 |
P 1 |
– P 2 |
M 1 |
M 2 |
M 3 |
|
ТМ8 |
P 1 |
– P 2 |
M 1 |
– M 2 |
– M 3 |
Примечание : P 1, P 2 — модули проекции тяги на оси 0 Y и 0 Z соответственно; FZ , FY , MX , MY , MZ — номинальные величины сил и моментов, создаваемых каждым ТМ соответственно.
Из данных, приведенных в таблице, следует, что двигатели ТМ1 и ТМ6, а также ТМ2 и ТМ5, ТМ3 и ТМ8, ТМ4 и ТМ7 создают одинаковые моменты и противоположно направленные силы. Таким образом, при включении последовательно двигателей ТМ1 и ТМ6 (ТМ2 и ТМ5, ТМ3 и ТМ8, ТМ4 и ТМ7) на равные промежутки времени создается чистый момент. Данная особенность схемы установки ТМ используется при расчетах их включений.
Принципы одновременного управления движением центра масс и вокруг него
Рассмотрим основные принципы одновременного управления движением центра масс и вокруг него. Пусть требуется коррекция орбиты преимущественно по наклонению с выдачей положительного приращения скорости по оси 0 Z . В этом случае коррекция орбиты осуществляется с помощью двигателей ТМ1–ТМ4. Пусть все двигатели создают номинальные и одинаковые силы и моменты. Допустим также, что коррекция проводится относительно инерциальной системы координат (ИСК) и связанные оси КА при маневре совпадают с осями ИСК. Тогда справедливы следующие уравнения:
F7 (At. + At., + At, + At,) = mA V7,
К (At. + At, - At, - At,) = mAV,,
M ( At. + At - At - At.) = AH, (1)
My(-Atv + At2 - At3 + AtJ = AHy, M7(At, - At2 - At3 + AtJ = AHZ, где At1, At2, At3, At4 — длительности включения ТМ; AVZ, AVY — требуемые приращения скоростей в боковом и трансверсальном направлениях; AHX, A HY, A HZ — требуемый сброс накопленного кинетического момента ИИО при проведении коррекции орбиты по осям; m — масса КА.
При коррекции орбиты только по наклонению приращение по трансверсали A VY = 0. Из сравнения второго и третьего уравнений (1) следует, что кинетический момент A HX не может быть сброшен при проведении данной коррекции орбиты. Что касается составляющих A HY, A HZ , то они могут быть сброшены, как это следует из решения системы уравнений (1).
Данный результат очевиден, поскольку в общем случае невозможно обеспечить нужное изменение пяти параметров (A VZ , A VY , A HX , A HY , A HZ ), используя четыре независимых переменных. Для разгрузки кинетического момента AHX необходимо включение пятого двигателя, одного из двигателей ТМ5–ТМ8. Однако включение любого из этих двигателей создает ускорение, противоположное требуемому приращению скорости КА, и, следовательно, увеличивает расход топлива на коррекцию орбиты. Уравнения (1) записаны для случая коррекции орбиты в ИСК. В действительности коррекции орбиты спутников связи серии «Ямал» осуществляются при ориентации КА в ОСК.
Запишем уравнения изменения импульса и кинетического момента КА (1) для случая маневра в ОСК. Изменение кинетического момента ИИО спроектируем в ИСК 0 xI yI zI , совпадающей с орбитальной в середине коррекции орбиты. За время коррекции происходит поворот ОСК относительно ИСК вокруг оси, перпендикулярной плоскости орбиты на угол и = и0 + ю0 t , где и — угол тангажа; t — время, отсчитываемое от начала маневра; и0 — угол тангажа при t = 0; ю0 — орбитальная угловая скорость. Положим также, что половина приращения угла тангажа за время работы одного ТМ A t мала и справедливы следующие упрощения: sin(rn0A t /2) = rn0A t /2; cos(rn0A t /2) = 1. Данные предположения справедливы, поскольку при выбранном значении MX и заданных размерах области вариации кинетического момента ИИО значение rn0A t /2 не превышает 6°. При маневре в ОСК первое, второе и пятое из уравнений (1) сохраняются. Третье и четвертое уравнения имеют следующий вид:
2 [MY.At.cos(u5.) -Afy.At.sin(u5j.)] = AHX, ^ [Mx.At.sin(uv.) + My. At: cos(us)] = AHy, где MXi, MYi — управляющие моменты, создаваемые i-м ТМ; At. — продолжительность работы i-го ТМ; υSi — угол тангажа, соответствующий середине времени работы i-го ТМ (i = 1, 2, 3, 4). При этом нулевое значение угла тангажа соответствует середине коррекции орбиты. В уравнениях (2) ∆HX, ∆HY — требуемые сбросы накопленного кинетического момента ИИО в системе координат 0xI yI zI. Пусть проводится коррекция орбиты только по наклонению и ∆VY = 0. Тогда, выбирая определенную последовательность включений ТМ, можно, следуя первому из уравнений (2), обеспечить изменение ∆HX в нужном направлении. Например, для создания положительного приращения ∆HX целесообразно в первой половине коррекции орбиты включать ТМ1 и ТМ3, во второй — ТМ2 и ТМ4. Таким образом при коррекции орбиты в ОСК появляется возможность изменения кинетического момента не только по осям Y, Z, но и по оси X.
Из уравнений (2) следует, что возможности изменения накопленного кинетического момента ИИО по оси 0 xI ограничены. С другой стороны, управляющие моменты по оси X в несколько раз превышают управляющие моменты по осям Y , Z (см. таблицу). Следовательно, разгрузка накопленного кинетического момента ИИО значительно эффективнее (по расходу топлива) по оси X , чем по осям Y , Z . Поэтому при коррекциях орбиты целесообразно в первую очередь проводить сброс накопленного кинетического момента по осям Y , Z , а по оси X при необходимости он может быть выполнен в конце операции.
Таким образом, при коррекции орбиты возможно обеспечить практически полный сброс накопленного кинетического момента системы ИИО. Однако для КА «Ямал», находящегося в постоянной орбитальной ориентации, нет необходимости такого сброса до малых значений. Достаточно обеспечить вхождение суммарного кинетического момента по окончании маневра в такую область, при нахождении в которой не потребуется разгрузки кинетического момента до следующей коррекции орбиты. Кроме того, наличие значительного кинетического момента ИИО позволяет обеспечить длительное поддержание ориентации в случае отказов датчиков внешней информации и инерциальных датчиков [1].
Алгоритм управления движением при маневрах, реализованный в СУД КА серии «Ямал»
Алгоритм расчета маневров, реализованный в СУД КА серии «Ямал», приведен в работах [2–5]. При его разработке в первую очередь решалась задача минимизации количества вклю- чений ТМ. Разработанный алгоритм позволяет совмещать трансверсальные коррекции орбиты с коррекциями орбиты по наклонению.
В основу расчета положена следующая последовательность операций. Траектория изменения кинетического момента маховиков H в связанной системе координат КА при работе каждого ТМ может быть представлена в виде винтового движения. При этом ось винта у каждого ТМ своя и направлена параллельно оси 0 Z 0 ОСК.
Последовательность расчетов включений тяговых модулей:
-
1. Значения ∆ VY , ∆ VZ перепроектируются из ортогональной системы координат в аффинную систему, направления осей которой совпадают с направлениями сил, создаваемыми ТМ1, ТМ2 и ТМ3, ТМ4 (и противоположны соответственно направлениям сил, создаваемых ТМ5, ТМ6 и ТМ7, ТМ8). Обозначим требуемые приращения скорости по данным осям ∆ V 12 и ∆ V 34, фактические отработанные приращения скорости — ∆ V 12ф и ∆ V соответственно. В зависимости от зна- 34ф
-
2. На каждом шаге расчетов выбор ТМ осуществляется по критерию
-
3. Расчет траектории кинетического момента H продолжается до тех пор, пока не выполняются одновременно условия
ков ∆ V 12 и ∆ V 34 определяется четверка ТМ, расположенная с одной стороны КА, которая должна обеспечить заданные приращения скорости. Не уменьшая общности изложения, предположим для наглядности, что выбраны ТМ1–ТМ4.
где e H и e ТM K — единичный вектор суммарного кинетического момента системы ИИО и единичный вектор момента ТМ с номером K соответственно; — значение единичного вектора кинетического момента маховиков, полученное после предыдущего включения тягового модуля.
Путем аналитических расчетов вычисляется пересечение винтовой траектории H с границей области вариации кинетического момента S +, подобной области S и уменьшенной на 10%. Два последних включения ТМ рассчитываются таким образом, чтобы ввести траекторию H в цилиндр с высотой, параллельной оси 0 Z , и размерами по всем осям, составляющими 79% размеров области вариации кинетического момента S .
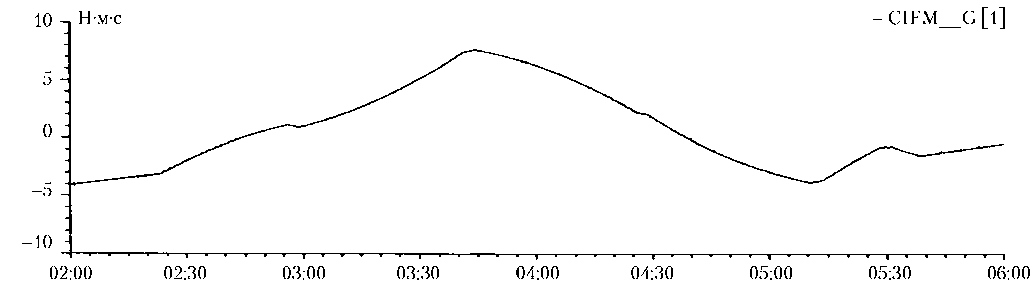
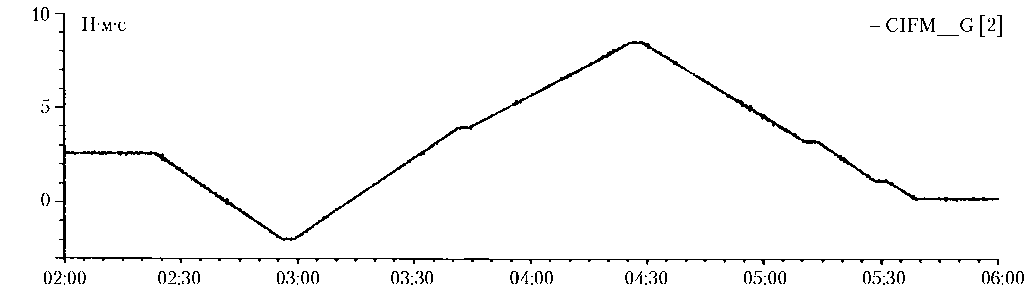
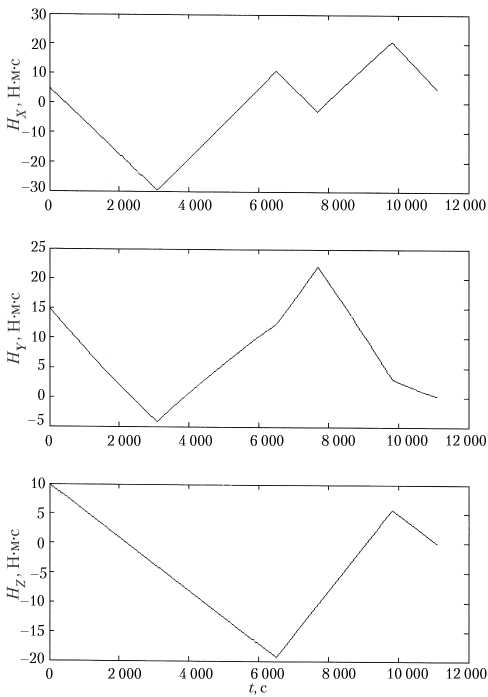
Д^,= |лГ|2ф|-|А^|2|>0, ^=K»hH При этом возможны следующие варианты окончания расчета: а) ∆V1 = 0; ∆V2 = 0. В этом случае импульс отрабатывается с использованием только четверки ТМ 1–ТМ4; б) ∆V1 = 0; ∆V2 = ∆2 > 0, здесь ∆2 — переработка импульса по направлению |Д V^J. Тогда последние включения двигателей ТМ3, ТМ4, создающие приращение импульса, равное ∆2/2, заменяются (полностью или частично) включениями двигателей ТМ8, ТМ7, имеющими, как было отмечено выше, такие же значения моментов и противоположно направленные силы. Таким образом устраняется переработка заданного приращения импульса; в) ∆V1 = ∆1 > 0; ∆V2 = 0, здесь ∆1 — переработка импульса по направлению |лур|. В этом случае последние включения двигателей ТМ1, ТМ2, создающие приращение импульса, равное ∆1/2, заменяются (полностью или частично) включениями двигателей ТМ6, ТМ5, имеющими такие же значения моментов и противоположно направленные силы. В случаях б) и в) для отработки импульса используются пять или шесть ТМ. Представленный алгоритм успешно используется в системах управления движением спутников серии «Ямал» более 12 лет. На рис. 2 показано изменение суммарного кинетического момента ИИО и корпуса КА при маневре по наклонению КА «Ямал-202» 8 октября 2012 года. Требуемое приращение скорости ∆VZ = 0,247 м/с, коррекция проводилась последовательными включениями ТМ2, ТМ4, ТМ1, ТМ3, ТМ2 и ТМ3, ее продолжительность составила 3 ч 18 мин 19 с. a) б) в) Рис. 2. Графики изменения суммарного кинетического момента корпуса КА и системы ИИО при маневре по наклонению: а, б, в — по осям X, Y, Z соответственно Управление кинетическим моментом КА на ВЭО Для управления движением центра масс КА дистанционного зондирования Земли (ДЗЗ) на ВЭО применяются восемь ТМ тягой 0,085 Н каждый. Векторы тяг двигателей параллельны плоскости 0yz КА. Тяга каждого двигателя имеет одинаковые по модулю проекции на оси 0y и 0z. Любой из двигателей создает момент относительно центра масс КА. Силы и моменты, создаваемые каждым из восьми двигателей тягой 0,085 Н, при отсутствии перекосов векторов тяг относительно номинальных значений, соответствуют приведенным в таблице при следующих значениях сил и моментов: P1 = 0,0586 Н; P2 = 0,0586 H; M1= – 0,01244 Н.м; M2= 0,00586 Н.м; M3 = 0,00586 Н.м. Из-за ограничений энергопотребления в каждый момент времени возможна работа только одного ТМ. Существуют два типа коррекции орбиты, каждый из которых включает, как правило, по два корректирующих импульса на витке. В первом случае коррекции орбиты проводятся в апогее и перигее, во втором — две симметричные коррекции в окрестностях точек пересечения орбиты с малой полуосью на нисходящей и восходящей частях орбиты. Управление движением вокруг центра масс при коррекциях осуществляется системой ИИО, в составе которой четыре маховика с кинетическим моментом 18 Н.м.с каждый. Оси вращения маховиков перпендикулярны разным непараллельным граням октаэдра. В первом приближении область вариации кинетического момента системы ИИО представляет собой шар радиусом 30 Н.м.с. К коррекциям на ВЭО предъявляются жесткие требования в части продолжительности: она не должна отличаться от расчетной более чем на несколько минут. Данное обстоятельство не позволяет включать двигатели, создающие силу, противоположную по знаку требуемому приращению скорости КА. Поэтому для КА на ВЭО невозможно использование алгоритмов, разработанных для СУД КА серии «Ямал». Виток состоит из двух частей примерно одинаковой продолжительности: рабочей в окрестности апогея, на которой включается целевая аппаратура, и дежурной, когда проводится гравитационная разгрузка накопленного кинетического момента ИИО и обеспечивается максимальное поступление электроэнергии с солнечных батарей. Коррекции орбиты с использованием ТМ могут осуществляться как на дежурной, так и на рабочей частях орбиты. На витке КА с использованием системы ИИО совершает угловые маневры для переходов из ориентации, требуемой для гравитационной разгрузки, к ориентации, необходимой на рабочем участке. Перед коррекцией орбиты на дежурном участке КА также должен переориентироваться из ориентации, требуемой для гравитационной разгрузки, в ориентацию, определенную для коррекции орбиты. Для реализации угловых маневров накопленный суммарный кинетический момент должен в общем случае находиться внутри шара радиусом, не превышающим 15 Н.м.с. Соответственно, начальные условия по накопленному кинетическому моменту на момент начала коррекций орбиты находятся, как правило, в пределах 15 Н.м.с. Алгоритм расчета включений ТМ при маневрах в апогее Длительность коррекции орбиты в районе апогея составляет примерно три часа. Пусть, например, требуется провести коррекцию орбиты c приращением скорости ∆VY при ориентации КА в ОСК. В этом случае она осуществляется включением двигателей ТМ1, ТМ2 , ТМ7 и ТМ8. Запишем уравнения изменений импульса и кинетического момента КА для случая маневра в ОСК. Изменение кинетического момента ИИО спроектируем в ИСК 0xI yI zI, совпадающей с орбитальной в середине коррекции орбиты. Получим следующую систему уравнений: a1 ∆t1 + a2 ∆t2 + a7 ∆t7 + a8∆t8 = ∆VY , a1 ∆t1 + a2 ∆t2 – a7 ∆t7 – a8∆t8 = 0, M ∆t + M ∆t – M ∆t – X1 1 X2 2 – MX8∆t8 = ∆HX + ∆HXOR,(4) –MY1∆t1 + MY2∆t2 + MY7∆t7 – – MY8∆t8 = ∆HY + ∆HYOR, MZ1∆t1 – MZ2∆t2 + MZ7∆t7 – – M ∆t = ∆H , Z8 8Z где a1, a2 , a7, a8 — ускорения при работе ТМ1, ТМ2, ТМ7 и ТМ8 соответственно; ∆HX, ∆HY, ∆HZ — требуемые изменения накопленного кинетического момента в ИСК 0xI yI zI; ∆t1, ∆t2, ∆t7, ∆t8 — продолжительности включений соответственно ТМ1, ТМ2, ТМ7 и ТМ8; MXi, MYi, MZi (i = 1, 2, 7, 8) — модули проекций управляющего момента ТМ на оси связанной системы координат; ∆HXOR, ∆HYOR — дополнительные изменения кинетического момента по осям 0xI, 0yI при реализации маневра в ОСК по сравнению с вариантом реализации маневра в системе координат 0xI yI zI. Переменные ∆HXOR, ∆HYOR описываются следующими уравнениями: ∆HXOR = MY1 υS1 ∆t1 – MY2 υS2 ∆t2 – – MY7 υS7 ∆t7+ MY8 υS8 ∆t8, ∆HYOR = – MX1 υS1 ∆t1 – MX2 υS2 ∆t2 + + M υ ∆t + M υ ∆t , X7 S7 7 X8 S8 8 где υS1, υS2, υS7, υS8 — углы тангажа, соответствующие серединам времени работы ТМ1, ТМ2, ТМ7 и ТМ8. При коррекции орбиты в апогее угол тангажа не превышает по модулю 11,5° и изменяется от положительного значения в начале коррекции к отрицательному — в конце операции. Уравнения (4), (5) записаны в предположении малости угла тангажа при маневре и малости приращений угла тангажа за время работы каждого ТМ. Уравнения (5) записаны для случая, когда каждый из ТМ включается один раз. В общем случае возможны неоднократные включения каждого тягового модуля. При расчете маневра в апогее помимо выдачи импульса должна решаться задача полного сброса накопленного кинетического момента по осям 0yI, 0zI и его уменьшения (не увеличения) по оси 0xI. Для этого есть различные способы. Например, на основе минимизации функции ΣHki2, где Hki (i = 1, 2, 7, 8) — модули векторов кинетических моментов ИИО по окончании каждого включения ТМ. При этом осуществляется перебор последовательностей ТМ при реализации маневра. Такой способ решения задачи минимизирует количество включений тяговых модулей. С практической точки зрения эффективен следующий способ расчета включений ТМ. Расчет коррекции орбиты в апогее проводится в два этапа в следующей последовательности: решая систему из первого, второго, четвертого и пятого уравнений выражения (4) для случая коррекции орбиты в ИСК (т.е. при углах тангажа, равных нулю), определяются расчетные длительности включения каждого из ТМ1, ТМ2, ТМ7 и ТМ8. По критерию (3) выбирается первый включаемый модуль. Затем для выбранного ТМ рассчитывается максимально возможная длительность его работы, т.е. определяется момент пересечения траектории, задаваемой вектором момента данного ТМ, со сферой, ограничивающей область вариации кинетического момента. Длительность включения выбранного ТМ определяется следующим образом: если расчетная длительность не превышает максимально возможную, то длительность включения равна расчетной длительности работы данного ТМ, иначе длительность включения равна максимально возможной. В последнем случае требуется, по крайней мере, еще одно включение данного ТМ. Далее рассчитываются второе и последующие включения до тех пор, пока все расчетные длительности включений ТМ не будут реализованы. Таким образом, определяется последовательность включаемых ТМ, длительности каждого включения и фактический кинетический момент ИИО на момент окончания коррекции орбиты. Определяется разность фактического и требуемого значений кинетического момента по оси 0yI на момент окончания операции (т.е. определяется ∆HYOR). К значению ∆HY прибавляется найденная разность. Затем проводится второй (окончательный) расчет включений ТМ, компенсирующий ошибку разгрузки по оси 0yI. В таком расчете управление кинетическим моментом по оси 0xI не проводится. Поэтому возможно некоторое увеличение (уменьшение) данного момента по окончании коррекции. Если на момент начала коррекции орбиты кинетический момент по оси 0xI существенен (более 30% от радиуса шара, вписанного в область вариации кинетического момента ИИО), то для предотвращения увеличения кинетического момента по оси 0xI при выборе первого включаемого ТМ наряду с критерием (3) вводится дополнительный показатель: выбирается (если это возможно) такой ТМ, проекция момента которого по оси 0Y имеет знак, противоположный знаку накопленного кинетического момента ИИО по оси 0xI. Целесообразность такого критерия следует из первого уравнения (5). Таким образом, при коррекции орбиты может обеспечиваться полный сброс кинетического момента по осям Y, Z. Также обеспечивается, по возможности, уменьшение кинетического момента по оси X. Заметим также, что на любом участке орбиты, если накопленный кинетический момент превышает по модулю 50% от радиуса шара, вписанного в область вариации, то проводится автоматическая разгрузка кинетического момента с использованием тяговых модулей. На рис. 3 приведены изменения кинетического момента системы ИИО при коррекции орбиты в апогее, полученные по результатам моделирования. Параметры коррекции орбиты: ΔVY = 0,26 м/с, продолжительность коррекции — 11 104 с, последовательно включались ТМ8, ТМ2, ТМ7, ТМ1, ТМ8. Рис. 3. Изменения суммарного кинетического момента ИИО при коррекции орбиты в апогее Алгоритм расчета включений ТМ при маневрах в перигее При проведении коррекций орбиты в перигее КА также ориентируется по связанным осям, параллельным осям ОСК. Однако орбитальная угловая скорость КА по нормали к плоскости орбиты в перигее в 40-60 раз больше, чем в апогее. При этом приращение угла тангажа за время работы одного ТМ не является малым, а может составлять десятки градусов. Поэтому алгоритм, разработанный для расчета коррекции в апогее, не может быть использован. Коррекции орбиты в перигее продолжаются до 30-40 мин, импульс направлен по трансверсали. Разработан алгоритм расчета включений ТМ для коррекций орбиты в перигее, состоящий из включений двух ТМ продолжительностью 15-20 мин каждое. Без ограничения общности рассмотрим случай, когда связанные оси совпадают с осями ОСК. Пусть необходимо выдать импульс по направлению оси 0Y0, который можно получить включениями двигателей из следующей четверки: ТМ1, ТМ2, ТМ7 и ТМ8. Заметим, что поскольку двигатели расположены косо относительно осей связанной системы коор- динат, то минимальное количество включений ТМ для выдачи импульса равно двум. При этом выбранные два ТМ должны иметь противоположные по знаку проекции силы по оси 0Z. При расчете маневра осуществляется перебор восьми вариантов последовательностей включений пар тяговых модулей: ТМ1–ТМ7 (первым включается ТМ1, вторым ТМ7), ТМ1–ТМ8, ТМ2–ТМ7, ТМ2–ТМ8, ТМ7–ТМ1, ТМ7–ТМ2, ТМ8–ТМ1, ТМ8–ТМ2. Из возможных вариантов, при которых траектория H не выходит за пределы области вариации кинетического момента S, выбирается вариант с наименьшим значением суммарного кинетического момента корпуса КА и системы ИИО на момент окончания маневра. Как показывают результаты моделирования, всегда существует последовательность включения двух ТМ, которая не приводит к увеличению суммарного кинетического момента. Алгоритм расчета маневров в окрестности точек пересечения орбиты с ее малой полуосью В окрестности точек пересечения орбиты с ее малой полуосью длительность коррекции орбиты составляет порядка одного часа и осуществляется четырьмя включениями, в общем случае разных ТМ, в среднем по 15 мин. При такой продолжительности включения ТМ изменение кинетического момента не превышает 30% области вариации, поэтому появляется возможность выбора вариантов последовательностей включений ТМ. Суммарный корректирующий импульс при проведении каждой из коррекций (на нисходящей и восходящей ветвях орбиты) выдается по направлению бинормали. Коррекции реализуются поочередными включениями двигателей, имеющих равные проекции векторов тяг на плоскость орбиты и перпендикулярно ей. Из-за проекций тяг на плоскость орбиты и ее эллиптичности возможно изменение и других орбитальных параметров (кроме наклонения) по результатам коррекций орбиты, в частности ее периода. Для исключения изменения периода орбиты необходимо выполнение следующего условия (при ориентации космического аппарата относительно ОСК в процессе коррекции орбиты) ∑ait ∆Ei = 0, (6) где ait — тангенциальное ускорение при включении i-го ТМ; ∆Ei — приращение угла эксцентрической аномалии за время работы i-го ТМ. Угол эксцентрической аномалии связан со временем t движения по орбите, отсчитываемым от точки перигея, следующим уравнением: t = [E - esin(£)], (7) где a — большая полуось; µ — гравитационная постоянная Земли; e — эксцентриситет орбиты. Полагая приращение угла эксцентрической аномалии за время включения отдельного ТМ малым, получим At = J—A£ [1-ecos(£0/|, (8) где ∆t — продолжительность работы ТМ; E0 — угол эксцентрической аномалии, соответствующий середине участка работы ТМ. Изменение периода орбиты ∆T по окончании работы i-го ТМ составит M= „2 61^-Ц a^^l -e\ где T — период орбиты. Суммарное изменение периода орбиты ∆T∑ после включения четырех ТМ можно записать A T,_ b^d .^Ep (10) где b= 6i-^- VT^ ц e2. Без ограничения общности будем полагать, что для коррекции наклонения используются двигатели ТМ1–ТМ4. При этом тяговые модули из пары ТМ1, ТМ2 создают тангенциальное ускорение одного знака, а из пары ТМ3, ТМ4 — другого. Изменение угла эксцентрической аномалии на 15-минутных интервалах операции составляют для восходящей коррекции орбиты: 0,191; 0,165; 0,145; 0,132 рад. Для нисходящей коррекции орбиты данные интервалы составляют те же значения в обратной последовательности. Анализ уравнений и изменения угла эксцентрической аномалии за время коррекции орбиты показывает, что для выполнения условия (6) целесообразно, чтобы в начале и в конце коррекции работали ТМ из одной пары, а в середине — из другой. В этом случае изменение периода орбиты не превышает допустимого значения. Пусть в начальный момент времени коррекции кинетический момент системы ИИО равен H0 и в процессе коррекции орбиты требуется изменить скорость КА по оси 0Z0 на ∆VZ. Используется следующий алгоритм расчета коррекции орбиты. Запишем в первом приближении приращения кинетического момента по осям 0yI, 0zI ИСК, совпадающей с орбитальной в середине коррекции орбиты, и изменения приращений скорости КА a1∆t1 + a2∆t2 + a3∆t3 + a4∆t4 = ∆VZ , a1∆t1 + a2∆t2 – a3∆t3 – a4∆t4 = 0, 1 1 2 2 3 3 4 4 (11) –M1Y ∆t1 + M2Y ∆t2 – M3Y ∆t3 + M4Y ∆t4 = ∆HY , M ∆t – M ∆t – M ∆t + M ∆t = ∆H , 1Z 1 2Z 2 3Z 3 4Z 4 Z где ai — ускорение КА при работе i-го ТМ (i = 1, 2, 3, 4); MiY, MiZ — модули проекций управляющих моментов при работе i-го ТМ на связанные оси 0Y, 0Z соответственно; ∆HY, ∆HZ — требуемые изменения кинетического момента системы ИИО в процессе коррекции орбиты в ИСК 0xI yI zI. По сравнению с уравнениями (4) в выражениях (11) отсутствует в правой части третьего уравнения составляющая ∆HYOR. Это связано с тем, что при выборе последовательности включений ТМ, согласно которой в начале и в конце коррекции орбиты включаются двигатели из одной пары, значение ∆HYOR близко к нулю. По формулам (11) определяются продолжительности работы ТМ1–ТМ4. При этом требуемые изменения кинетического момента системы ИИО по осям 0yI, 0zI ограничиваются значениями, составляющими 10% от размера шара, вписанного в область S. Для сброса положительного кинетического момента по оси 0xI, как это следует из уравнений (2), в первой половине коррекции необходимо включать ТМ1 и ТМ4 соответственно, для сброса отрицательного кинетического момента по оси 0xI необходимо в первой половине коррекции включать ТМ2 и ТМ3. Всего возможно восемь вариантов последовательностей включений ТМ: ТМ1–ТМ3–ТМ4–ТМ2 (первым включается ТМ1, вторым ТМ3, третьим ТМ4, четвертым ТМ2), ТМ1–ТМ4–ТМ3–ТМ2, ТМ2–ТМ3–ТМ4–ТМ1, ТМ2–ТМ4–ТМ3–ТМ1, ТМ3–ТМ1–ТМ2–ТМ4, ТМ3–ТМ2–ТМ1–ТМ4, ТМ4–ТМ1–ТМ2–ТМ3, ТМ4–ТМ2–ТМ1–ТМ3. Из возможных вариантов, при которых траектория H не выходит за пределы области вариации кинетического момента S, выбирается вариант с наименьшим значением суммарного кинетического момента корпуса КА и системы ИИО на момент окончания маневра. Заключение Разработаны алгоритмы управления накопленным кинетическим моментом инерциальными исполнительными органами космического аппарата при проведении маневров с использованием тяговых модулей, расположенных по схеме, обеспечивающей одновременное создание сил и управляющих моментов относительно центра масс КА. Для КА серии «Ямал» созданы алгоритмы, обеспечивающие эффективное одновременное управление движением центра масс и вокруг него, а также минимизирующие количество включений тяговых модулей. Как показал 12-летний опыт эксплуатации космических аппаратов серии «Ямал», применение разработанных алгоритмов привело к исключению расхода топлива на разгрузку накопленного кинетического момента инерциальными исполнительными органами на участках полета между коррекциями орбиты. Для системы управления движением разрабатываемого в настоящее время КА дистанционного зондирования Земли на высокоэллиптической орбите созданы три разных алгоритма расчета включений тяговых модулей: в апогее, перигее и окрестностях точек пересечения орбиты с ее малой полуосью. Использование данных алгоритмов обеспечивает решение задач, поставленных перед системой управления движением КА дистанционного зондирования Земли. Приводятся результаты летно-конструкторских испытаний и математического моделирования маневров космического аппарата на геостационарной и высокоэллиптической орбитах, которые свидетельствуют об эффективности разработанных алгоритмов.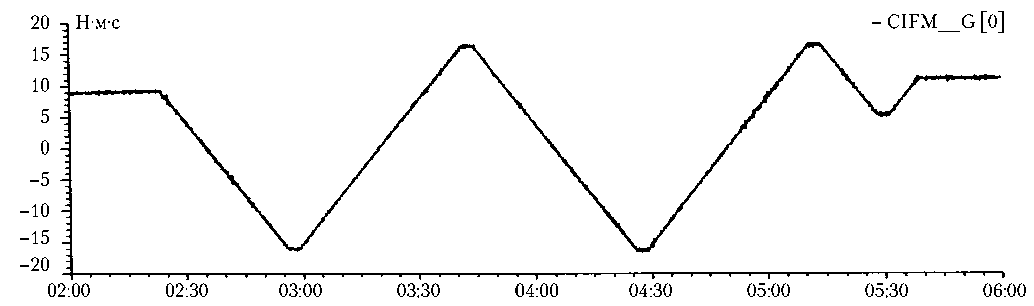
Список литературы Одновременное управление движением центра масс и вокруг центра масс при маневрах космических аппаратов на геостационарной и высокоэллиптических орбитах c использованием электрореактивных двигателей
- Платонов В.Н. О возможности длительного поддержания ориентации геостационарного спутника без использования датчиков внешней информации и инерциальных датчиков//Космические исследования. 2009. Т. 47. № 3. С. 263-270.
- Кульба В.В., Микрин Е.А., Павлов Б.В., Платонов В.Н. Теоретические основы проектирования информационно-управляющих систем космических аппаратов. М.: Наука, 2006.
- Платонов В.Н. Управление кинетическим моментом при проведении маневров КА «Ямал-100» с использованием электрореактивных двигателей: Сб. статей/Труды РКТ. Сер. XII. Вып. 1. Королев: РКК «Энергия», 2002. С. 92-97.
- Патент RU 2112716 С1. МКИ B 64 G 1/26, 1/28. Российская Федерация. Способ управления космическим аппаратом с помощью реактивных исполнительных органов и система для его реализации. Бранец В.Н., Ковтун В.С., Платонов В.Н., Шестаков А.В.; заявитель и патентообладатель -ОАО «РКК «Энергия»; заявка 97107878/28; приоритет от 13.05.1997//Изобретения. 1998. № 16.
- Патент RU 2124461 С1. МКИ B 64 G 1/26, 1/24, 1/40. Российская Федерация. Способ управления космическим аппаратом, снабженным реактивными двигателями с направленными под углом к осям связанного базиса и смещенными относительно центра масс аппарата линиями действия тяг, система для реализации способа, блок реактивных двигателей системы. Бранец В.Н., Земсков Е.Ф., Ковтун В.С., Платонов В.Н., Шестаков А.В.; заявитель и патентообладатель -ОАО «РКК «Энергия»; заявка 97118643/28; приоритет от 12.11.1997.//Изобретения. 1999. № 1. Статья поступила в редакцию 25.12.2012 г.


