Ограничение колебаний электромагнитного момента асинхронного двигателя при скалярном частотном управлении

В системах частотного асинхронного электропривода со скалярным управлением, использующихся на металлургических предприятиях, в том числе на механизмах, работающих в интенсивных повторно-кратковременных режимах, например, на мостовых кранах, переходные процессы характеризуются колебаниями переменных асинхронного двигателя, в том числе и выходных – момента и скорости, что ограничивает область применения системы скалярного управления. В работах [1–4] исследована возможность улучшения динамических свойств АД в системе частотного электропривода со скалярным управлением путем введения дополнительных корректирующих контуров, например, в исследовании [2] – путем регулирования сигнала задания напряжения в функции активной составляющей тока статора. Остаются актуальными проведение исследований и практическая реализация наиболее эффективных методов повышения устойчивости системы частотного асинхронного электропривода со скалярным управлением путем использования различных методов коррекции.

Теоретический анализ

Для аналитических исследований целесообразно использовать запись уравнений асинхронного двигателя в операторной форме в системе координат Х – Y , вращающейся со скоростью электромагнитного поля статора, что позволяет перейти от гармонических векторных переменных к амплитудным значениям. В этом случае основные уравнения, описывающие асинхронный двигатель, можно представить в виде [1, 5]:

U i x (p) = ii х ( p ) • Ri + p Vi x (p )-toi Vi y (p);(i) U 1 y (p) = iiy (P) • Ri + pViy (p) + toi Vi x (p);(2) 0 = i2 XR 2+ p V 2 x (p) - 5 ®i( p )V2 y (p);(3)

0 = i2 yR 2+ p ^2 y (p) + 5 ®i( p )V2 x (p);(4)

5 = toi(p) -ю(p) = Аго(p) ;(5)

® i ⁽ p )        ® i ⁽ p ) ’

Vix (p) = Liiix (p) + Lmi2x (p);(6)

Viy (p) = Liiiy (p) + Lmi2 y (p);(7)

V 2 x ( p ) = L 2 i2 x ( p ) + Lmiix ( p );(8)

V2 y (p) = L 2 i2 y (p) + Lfflii y (p);(9)

M = 2 • LT • pn '(V2xiiy -V2yiix );

M (p ) - Mc (p) = p • J •«( p), где U1 – напряжение статора; i1 – ток статора; R1 – активное сопротивление цепи статора; Vi - потокосцепление статора; V 2 - потокосцепление ротора; го - скорость вращения ротора; toi = гоk - скорость вращения поля статора и системы координат; L1 – индуктивность статора; L 2   - приведенная индуктивность ротора;

L_m – взаимная индуктивность статора и ротора; J – момент инерции двигателя; s – скольжение двигателя; p_n – число пар полюсов двигателя.

После преобразований исходных уравнений (1)–(11), которые могут быть выполнены различным образом, можно представить математическую модель асинхронного двигателя в виде структурных

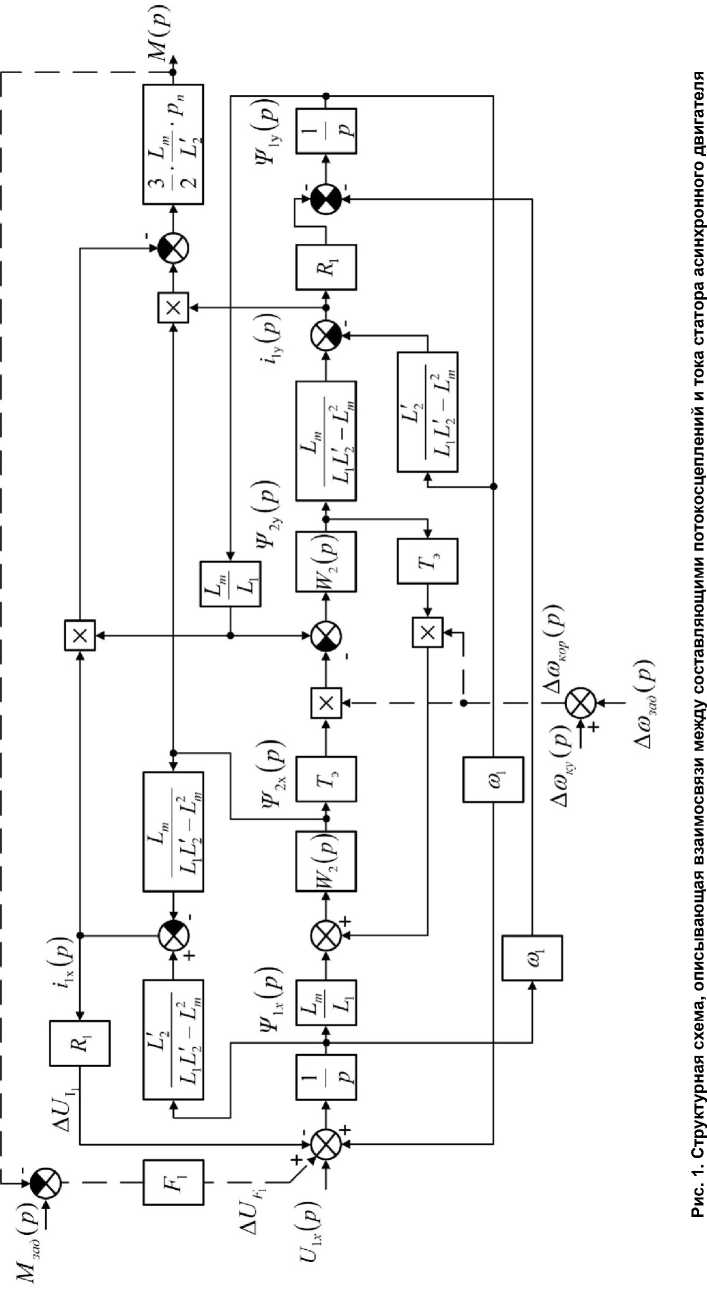
схем различных конфигураций [1, 5]. Структурная схема асинхронного двигателя, построенная с использованием преобразованных уравнений (1)–(11), удобная для структурного анализа динамических свойств двигателя, приведена на рис. 1, где показаны некоторые возможные реализации корректирующих воздействий.

Данная схема имеет большое количество эле-

ментов и замкнутых контуров, поэтому сложна для анализа, но с учетом предложенного в работе [1] допущения о возможности стабилизации потокосцепления статора, что с достаточно высокими точностью и быстродействием достигается в современных векторных системах асинхронного электропривода, например, прямого управления моментом [6], структурная схема может быть существенно упрощена и приведена к виду, показанному на рис. 2.

В упрощенной схеме, полученной при допущениях V 1 ( p ) = ¥ 1 x ( р ) = const, когда вектор потокосцепления статора находится на оси Х , и Аю эл = Аю ■ p n = A f ■ 2 п = const рассматривается

только внутренний линеаризованный замкнутый контур исходной схемы (см. рис. 1). Передаточная функция, характеризующая инерционность обмот-

ки ротора имеет вид:

W 2 (P) =

.

Т э р + 1

Постоянная времени обмотки ротора опреде-

ляется:

т

э

L 1 L 2 — L m

LR 2

Применив правила структурных преобразований для структурной схемы (см. рис. 2), определим приращения проекций потокосцеплений ротора при изменении потокосцепления статора 5V 1 x ( p ) :

5V 2 x ( P ) =

W 2 ( p ) ■ ( L_m IL 1 ) ^5^ 1 x ( p ) ^A( p )

^5V 2 y ( p ) =

(Lm IL1)■ W2 (p)■ T ■АЮл-6Y,x (p) A( p)

. (15)

Характеристическое уравнение системы

A ( p ) = 0 имеет вид:

A(p) = 1 + W,2 (p)■ T32 ■Ato^, = 0.(16)

После подстановки выражения передаточной функции из уравнения (12), получим характеристическое уравнение в виде:

(Тэр +1)2 + (Ato3, ■ ТJ2 = 0.(17)

Корни имеют следующий вид:

Р1,2 =-а± j fi = - ± j Мл.

T _э

Выражение (18) показывает, что упрощенная модель асинхронного двигателя представляет собой колебательную систему, поэтому вращение реального двигателя сопровождается существенными колебаниями электромагнитного момента, влияющими на процесс движения механизма.

Для подавления колебаний в замкнутом контуре (см. рис. 2) можно воздействовать на величину круговой частоты ЭДС ротора Ato _3J1 путем изменения частоты напряжения статора f ₁, что потребует при построении системы управления асинхронным электроприводом с улучшенными динамическими свойствами реализацию корректирующего контура в канале регулирования частоты. Колебания электромагнитного момента асинхронного двигателя, работающего в системе частотного скалярного управления, можно ограничить, используя другие методы коррекции, среди которых можно отметить реализацию отрицательных обратных связей по измеряемым или рассчитываемым переменным двигателя, что позволяет воздействовать на мгновенные значения напряжения статора. На рис. 1 пунктирными линиями показана упрощенная реализация возможных каналов коррекции, влияющих на динамику асинхронного двигателя.

Построение и описание работы предлагаемой системы частотного асинхронного электропривода со скалярным управлением

Структурная схема силовой части электропривода приведена на рис. 3. Преобразователь частоты содержит выпрямитель 1, емкостный фильтр 2, автономный инвертор напряжения (АИН) 3. Инвертор построен по мостовой схеме и выполнен на полностью управляемых IGBT-транзисторах с об-

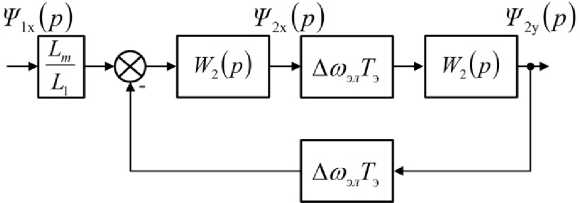
Рис. 2. Упрощенная структурная схема, описывающая взаимосвязи между составляющими потокосцеплений асинхронного двигателя

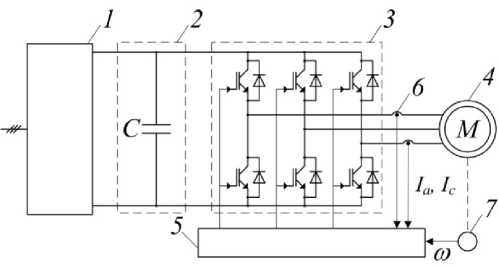
Рис. 3. Структурная схема силовой части электропривода

ратными диодами. К выходу инвертора подключен трехфазный асинхронный двигатель с короткозамкнутым ротором 4. Сигналы, пропорциональные выходным токам инвертора, поступают в систему управления 5 от датчиков тока 6. Для определения текущего значения скорости в системе используется датчик скорости 7.

Функциональная схема системы управления асинхронным электродвигателем со скалярным управлением приведена на рис. 4. В скалярной системе сигналы задания на частоту и напряжение электродвигателя поступают по двум взаимосвязанным каналам и дополняются корректирующими сигналами. Рассмотрим структуру системы скалярного управления, применяемую в типовых преобразователях частоты. Сигнал задания на частоту формируется задатчиком интенсивности 1. Сигнал задания на напряжение U ₀ ^* формируется в блоке 4, который имеет линейную характеристику, отображающую зависимость напряжения от сигнала заданной частоты f ^* .

Для защиты от перегрузки по току в системе применяется контур ограничения выходного напряжения. Сигналы фазных значений выходного тока статора поступают от датчиков тока в блок вычисления 10, выходом которого является значение модуля тока статора. Далее полученный сигнал поступает на сумматор, где сравнивается со значением максимально допустимого тока статора, поступающего от блока задания 11. Контур ограничения тока статора действует, только когда значение модуля тока статора превышает значение максимально допустимого тока. Для этого в системе предусмотрен блок ограничения 12. Далее сигнал рассогласования поступает на пропорционально-интегральный регулятор 13, выходом которого является сигнал коррекции напряжения, ограничиваемый в блоке ограничения 14, который поступает в виде отрицательной обратной связи на сумматор в канал задания напряжения. Для защиты от превышения по напряжению статора сигнал задания на напряжение ограничивается в блоке ограничения 5, выходом которого является результирующее значение заданной амплитуды напря- жения статора U * . Сигналы задания на амплитуду напряжения и частоту поступают в блок управления 6, который формирует задания на амплитуды фазных напряжений. Сигналы Ua* , Ub* , Uс* поступают в блок управления электронными ключами инвертора напряжения 7, использующего в своей основе пространственно-векторную широтноимпульсную модуляцию.

Результаты исследований

Описанная система асинхронного электропривода переменного тока со скалярным управлением была смоделирована в программной среде MATLAB Simulink [7]. Блок схема компьютерной модели системы электропривода показана на рис. 5.

Для исследования работы системы был взят асинхронный двигатель с короткозамкнутым ротором АДЧР355SMB6У2 ( P ном = 200 кВт, U ном = 380 В, I ном = 382 А). С помощью компьютерной модели были построены графики зависимости от времени скорости и момента двигателя для описанной системы электропривода, обозначенные на рис. 6, 7 цифрой 1. На временном интервале 0–3,5 с происходит разгон двигателя до частоты 35 Гц с номинальным статическим моментом на валу электродвигателя, равным 1924 Н·м. На временном интервале 3,5–4,5 с двигатель работает в статическом режиме с номинальным моментом статическим. В момент времени 4,5 с происходит скачкообразный сброс нагрузки до 75 % от номинальной. На временном интервале 4,5–5,5 с двигатель работает в статическом режиме с пониженным моментом статическим. На временном интервале 5,5–6 с производится разгон двигателя до частоты 40 Гц. На временном интервале 6–7,5 с двигатель работает в статическом режиме с пониженным моментом статическим. В момент времени 7,5 с происходит скачкообразный наброс нагрузки до 137,5 % от номинальной. На временном интервале 7,5–9 с двигатель работает в статическом режиме с повышенным моментом статическим. Как видно из полученных графиков система характеризуется высокой колебательностью момента электродвигателя и колебаниями скорости.

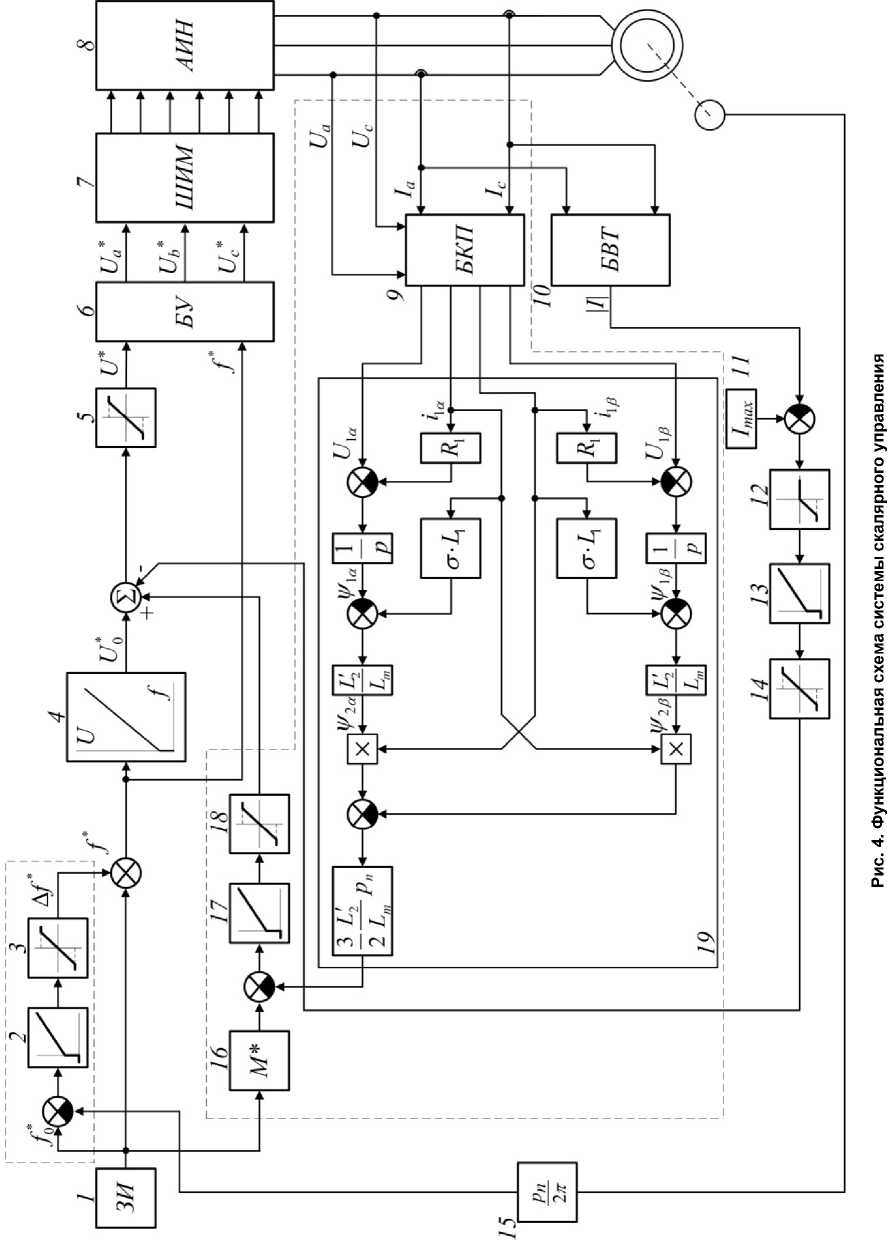
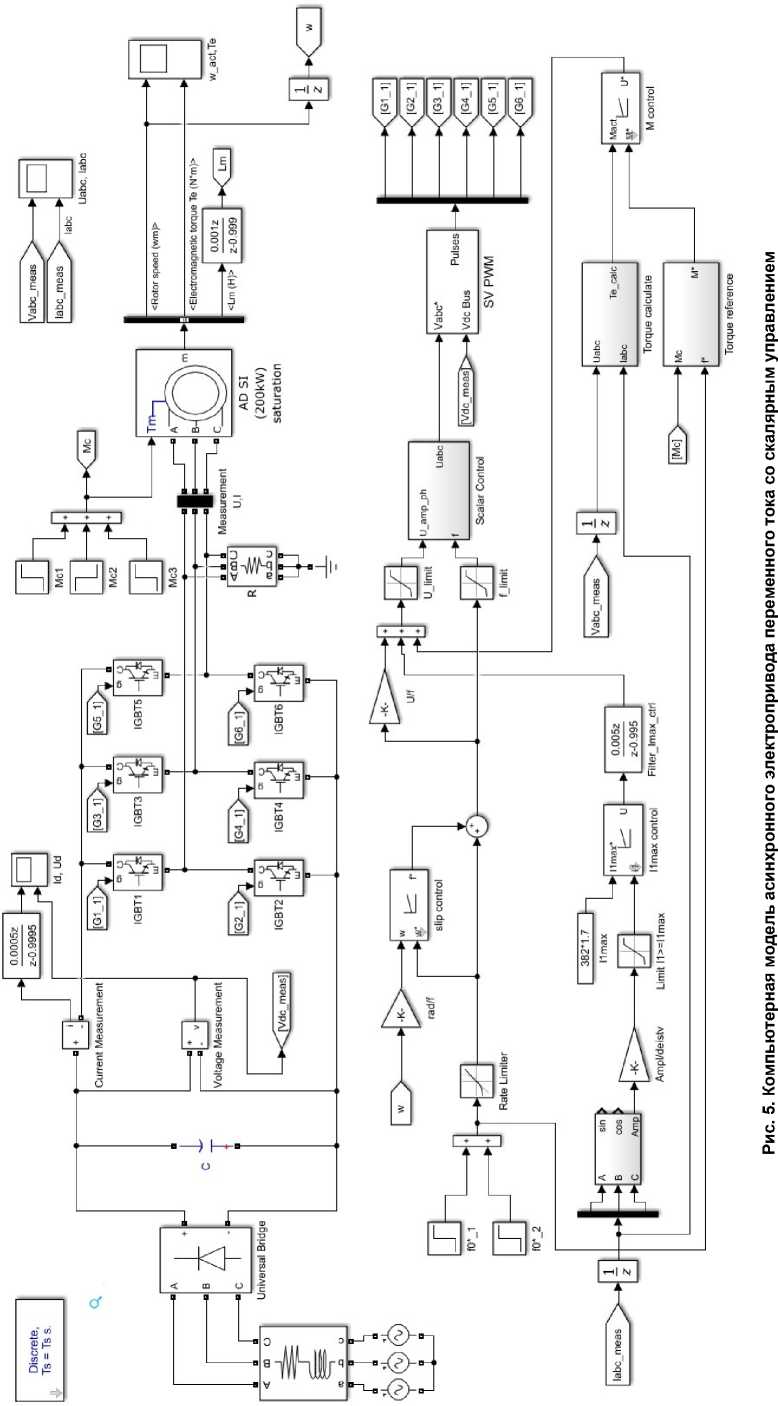
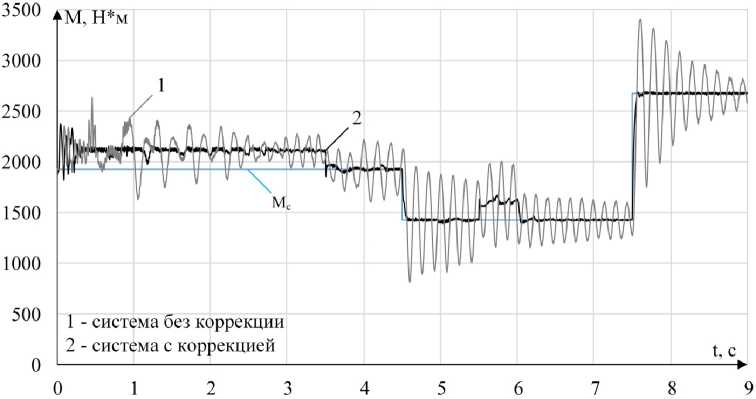
Рис. 6. Графики изменения момента на валу электродвигателя

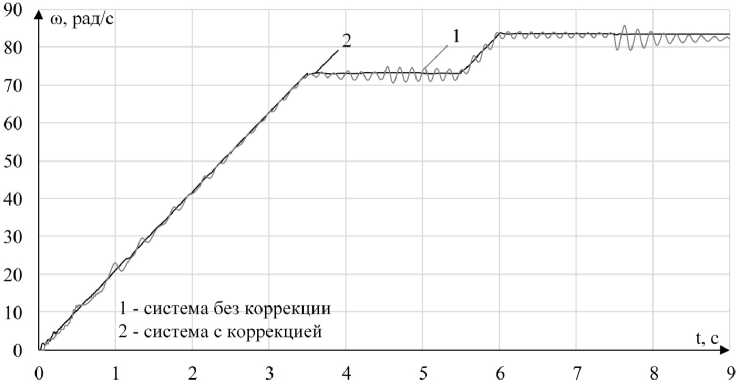
Рис. 7. Графики изменения скорости вращения электродвигателя

Значения максимального отклонения электромагнитного момента от среднего значения на различных участках работы электропривода

Интервал времени, с	Среднее значение момента, Н·м	Максимальное отклонение момента от среднего значения, %
		Система без коррекции	Система с коррекцией
0–3,5	2100	25	6
3,5–4,5	1924	16,8	3,8
4,5–5,5	1424	43,8	2,3
5,5–6	1566	27	5,3
6–7,5	1424	19	1,8
7,5–9	2674	34,5	0,5

Значения максимального отклонения электромагнитного момента от среднего значения на каждом из указанных участков работы приведены в таблице. Область низких частот в интервале 0–3 Гц не рассматривается, так как не является характерной для работы скалярных систем.

Указанные значения отклонений оказывают негативное влияние на динамические и статиче- ские характеристики системы и недопустимы для большинства механизмов.

В современных скалярных системах управления частотным асинхронным электроприводом [3] используется дополнительный канал коррекции задания частоты питающего напряжения, обеспечивающий компенсацию скольжения при изменении нагрузки на валу двигателя. Он содержит про- порционально-интегральный регулятор 2, на вход которого поступает сигнал рассогласования между заданной частотой и фактической частотой вращения двигателя. Значение фактической частоты вращения поступает от блока преобразования 15, на вход которого приходит сигнал обратной связи по скорости ω от датчика скорости. Выход регулятора 2 ограничивается в блоке ограничения 3, где формируется сигнал коррекции Δf * , поступающий на сумматор, выходом которого является *

сигнал задания f на частоту выходного напряжения. Применение данной системы коррекции недостаточно улучшает динамику системы, так как не позволяет добиться точности поддержания электромагнитного момента двигателя.

Для повышения точности поддержания момента и скорости электродвигателя в динамических и статических режимах предлагается дополнить систему скалярного управления с компенсацией скольжения (см. рис. 2), корректирующим устройством, состоящим из блоков 9, 16–19, действующим в функции отклонения момента от заданного значения и оказывающим воздействие на канал задания амплитуды напряжения статора.

Рассмотрим систему электропривода с дополнительным корректирующим устройством, содержащим наблюдатель электромагнитного момента асинхронного двигателя. В блоке координатных преобразований 9 происходит переход от измеренных фазных значений напряжений и токов статора к двухфазной неподвижной системе координат α - β . Выходными сигналами блока координатных преобразований являются значения напряжения статора U _α , U _β и тока статора I _α , I _β . Значения токов и напряжений в двухфазной неподвижной системе координат поступают в блок вычисления момента 19, использующего в своей основе выражение электромагнитного момента:

M = 32 ⋅ ^L _L ^m ⋅ p n ⋅ ( Ψ 2 α i 1 β - Ψ 2 β i 1 α ) . (19)

Вычисленное в блоке 19 значение электромагнитного момента M поступает на узел сравнения, где вычитается из заданного значения электромагнитного момента M * , формируемого в блоке задания 16. Задание на электромагнитный момент формируется в функции заранее известного статического момента на валу электродвигателя, а также в функции задания на частоту, поступающего от блока 1. При наличии изменяющегося во времени задания на частоту задание на момент увеличивается на коэффициент k = 1,05…1,15, экспериментально определяемый при настройке системы из условия обеспечения требуемого динамического момента. Сигнал рассогласования между заданным и фактическим значением момента поступает на пропорционально-интегральный регулятор 17 и ограничивается в блоке огра- ничения 18. Результирующий сигнал коррекции поступает в виде положительной обратной связи в канал задания амплитуды напряжения статора U* .

Разработанная система асинхронного электропривода переменного тока со скалярным управлением и корректирующим устройством была смоделирована в программной среде MATLAB Simulink [7]. Полученные графики зависимости скорости и момента двигателя от времени обозначены на рис. 6, 7 цифрой 2. Значения максимального отклонения электромагнитного момента от среднего значения для всех участков работы приведены в таблице. Полученные на компьютерной модели частотного асинхронного электропривода со скалярным управлением результаты показывают эффективность действия предлагаемых корректирующих средств.

Выводы

• 1.    Применение системы коррекции сигнала задания напряжения двигателя в функции вычисляемого электромагнитного момента и сигнала задания частоты питающего напряжения позволяет получить графики переходных процессов при пуске электропривода и регулировании скорости с максимальным отклонением момента от среднего значения, не превышающего 5 %, обеспечено подавление колебаний скорости двигателя в переходных режимах.

• 2.    Повышена точность поддержания скорости в установившемся режиме, отсутствуют колебания на графике скорости при переходе от пускового режима в установившийся режим и после изменения нагрузки на валу двигателя.

Работа выполнялась при поддержке гранта РФФИ № 17-48-480492 «Анализ, математическое моделирование и оптимизация управления электромеханическими системами с электроприводами переменного тока мехатронных устройств, манипуляторов и грузоподъёмных механизмов»