Ограниченность интегрального оператора, действующего в весовых пространствах Лоренца
Автор: Ломакина Е.Н.
Журнал: Вестник Хабаровской государственной академии экономики и права @vestnik-ael
Рубрика: Методы и методология математики в экономике
Статья в выпуске: 2, 2019 года.
Бесплатный доступ
В статье получен критерий ограниченности одновесового оператора Харди, действующий в весовых пространствах Лоренца
Интегральный оператор, оператор харди, банаховы функциональные пространства, пространства лоренца
Короткий адрес: https://sciup.org/143168839
IDR: 143168839 | УДК: 51
Текст научной статьи Ограниченность интегрального оператора, действующего в весовых пространствах Лоренца
Линейное нормированное пространство
X = V:
llfll^
-
(1) ll/llx определена для каждой измеримой по Лебегу функции / на полуоси, и f E X в том и только в том случае,
если / — 0 почти всюду (п.в.);
(2) ll/llx = II in llx для всех fEX ;
-
(3) если O^f ^9 п.в., то
Hfllx S llyllx;
-
(4) если 0
п.в., то
Hfllx T Hpllx;
-
(5) если E с X , mesE < oo, то
IlZsIlx < 00;
-
(6) если mesE < oc, то
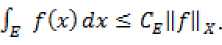
если Hfllx
00 ;
Например, пространство Лебега
Lp = Lp (R, tig) измеримых функций c ко-
Il/h = 0 в том и только в том случае,
нечной нормой
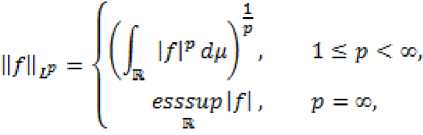
является банаховым функциональным пространством.
Также банаховыми функциональными пространствами являются пространства Лоренца, которые будем рассматривать в разделе 2.
Теория банаховых функциональных пространств подробно изложена в монографии [1].
Пусть , – два весовых банаховых функциональных пространства измеримых функций, заданных на, где весовые функции измеримые по Лебегу, положительные и конечные почти всюду на
Рассмотрим интегральный оператор Хардивида
,(1.1)
где неотрицательная весовая функция.
Для данного банахова функционального пространства двойственным пространством Х является пространство X = с '• J. "V' < - ?.:.'f ;<; "' £ л;, снабженное нормой
.(1.2)
Пространство также является банаховым функциональным пространством, причем равенство
(1.3)
выполняется для всех . Пространства и являются полными линейными нормированными пространствами и . [1]
Неравенство Гельдера ir„“rsl S ll/IMIsll,
(1.4)
выполняется для всех и
Принцип двойственности. T:X ->Y является ограниченным линейным оператором таким, что ||Т/||Х< С||/||х для всех fEX с положительной константой С тогда и только тогда, когда
-
(i) ||T'S||x.
S||r -
(ii) для всех g E Y ,
-
(iii) где двойственный оператор T\ Y'-^X определяется по формуле (iv)
№Л д = I®f(T'g') ,
(1.5)
(1.6)
или
(v)|f0W)5|^C||/||x||5||y. для всех fEXи8EY‘, с некоторой константой C.
Положительная константа c определяет норму 117’11 , и, таким образом, l|7’llx^y — 117* lly-^x
Двойственный оператор T'-. Y'^X и
^Tf^g^u^dx = SqT gtoftov^dx . (1.7)
Пространства Лоренца
Если измеримая функция ƒ определена на измеримом пространстве ((0, °0), v(x)dx).
Для
1 < r, S < oc, весовой функция »(x) на K+ = (0,x), пространство Лоренца L” = L-(R+) состоит из всех измеримых функций ƒ таких, что
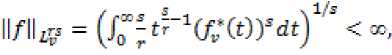
(2.1)
где невозрастающая перестановка fy функции ƒ относительно v(x~)(ix определяется следующим образом f^t) = infU > 0 : v({% > 0 : |/(x) | > Л}) < t}
(2.2)
Заметим, что ^) = 4
v(x)dx, и и/ni7 = ил^=a0°°if(t)rxt)dOVr
Пространство Лоренца ^v является банаховым фнкциональным пространством, если 1 < S < T, 1 < S < Г < X. Если же 1 < r < s < x , то будет банаховым фнкциональным пространством относительно другой нормы, эквивалентной (2.1):
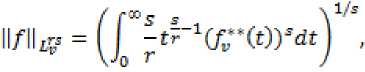
где ГЧ0=;^Г(т)<1т, t>0
Пространства Лоренца ^ обладают абсолютно непрерывными нормами.
Напомним, что норма в банаховом функциональном пространстве X абсолютно непрерывна, если для всех fEX, \fXEnXx ^ ° для каждой последовательности множеств {EJ c JR4 таких, что Z^W "* ° п.в.
Для пространства ^v> двойственным пространством ^V является пространство
,
(2.3)
снабженное нормой
I^Lry = sup ^"|f(x)5(x)v(x)dx| : l/l^ < 1].(2.4)
Неравенство Гельдера
|/^/(%)у(%)г(х)^х| < ifi^Jsl^y,(2.5)
где
- + - = 1, - + - = 1, 1 < r < X, 1 < s < x r r's s'
и
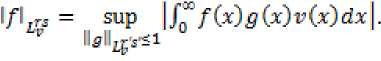
(2.6)
Нашей целью является получение критерия ограниченности, оператора Харди, действующего в весовых пространствах Лоренца T : L7№+) -^ L^№ в области
1 < p, q < х, 1 < r,s < x и max (r, s} < q вида
Tfto = /^(O/XOdr, x > 0,
(2.7)
где неотрицательная весовая функция u(t) 6 Lrs (0, x) для всех x > 0.
Мы исследуем более общий оператор, чем в статье [2], и другой случай индексов, чем результаты исследований [3]. Доказательство достаточности в критерии ограниченности оператора проводится с
помощью принципа двойственности банаховых функциональных пространств.
Ограниченность оператора Харди в пространствах Лоренца
Для доказательства ограниченности оператора (2.7) необходима следующая лемма.
Лемма 1 [2] . Пусть 1 < r,s < x, max (r,s) < q, и f^} – последовательности измеримых, попарно непересекающихся интервалов таких, что UEk = (0,x).
Тогда
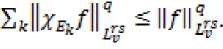
(3.1)
Доказательство. Используя неравенство Минковского с параметром j < 1и неравенство Йенсена при r - 1 , получаем
^iMir,. = ^:w\to,,rst”idtT'’5 ^^k(xE.,f)to^f'^st■-^dt\','' 5 ($;wt^2-W,s = ишь. □
Критерии ограниченности оператора (2.7) содержатся в следующей теореме.
Теорема 1. Пусть 1 < p, q < x, 1 < r,s < x, max {r, s} < q .
Оператор
T : L7(IR+) -» L”(^+) вида (2.7) ограничен тогда и только тогда, когда
(3.2)
t>0
Более того, Л < liril^iP? < 4Л.
Доказательство. Необходимость. Если T : L7№+) -^ L^№ ограничен, тогда, используя аксиомы (2), (3) банахова функционального пространства для произвольного t > 0 и всех неотрицательных f E l;4r+) таких, что f(y)u(y) > О, получаем
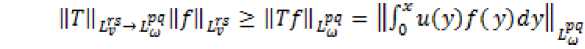
2 11/[м)11гР/ои<У)Ау)^У = I|Z[^|| Р1/^м(у)м(у)Лу)^ .
jrV
Таким образом, приходим к неравенству llz[to)Lq/omZ[at](y)u(y)fM < lini^^Hfii^.
^P||fllIpJZ[f^|LpJoeZ[o,t](y)u^ S sup IITII^^HfH^.
Полагая fl(y) = Z[o.t]6')u6')i' ^ и учитывая, что /СуХу) 2 o, в силу формулы (2.4), получаем
/-00
sup ZMkXyX^OfMXDdy = Izto^ur-1! r.s..
If IlP0 P
A(0 = llz[№)l|- IZm"17"1^' 5 H^L?^^4.
Следовательно, A - М^-^И для всех t > c , и оценка снизу доказана.
Достаточность. Из принципа двойственности следует, что для оценки сверху достаточно доказать неравенство co
I Tf(x)fl(x)w(x)dx < C||/,||LrS||5l|£p'q 0
для всех / E l;4r+) и 9 E L^ (R+).
По условию 1 < p, q < ос, 1 < r, s < ос и max [r, s) < q . Предположим, что /■(t)u(t) > 0. Пусть m £ Z такое, что ^u^f(r-)dT G (2m, 2m+1]. Тогда найдется возрастающая последовательность ^xk^k=-oc , что для к < m — 1 выполняется
2k = ^ku(TW)dT = $^u(TW)dT, (3.3)
и
2m = ^mu(T)f(T)dT.
(3.4)
Положим Ек = [xk,xk+J к<т—1, а ^+i = ж-
Таким образом, получаем последовательность попарно непересекающихся интервалов
Г^к) таких, что
Uk (3.5) Если /0”^(T)f(r)dT = ос, тогда (3.3) выполняется для всех к Е Z и (3.4) остается справедливым. В силу формул (3.3) и (3.4) заключаем, что Tf^ < 2k+1 для х Е Ек, к < тп. (3.6) Следовательно, ПТН^^ <4Л. □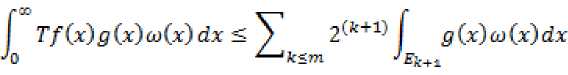
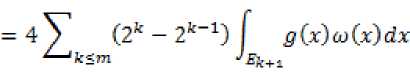
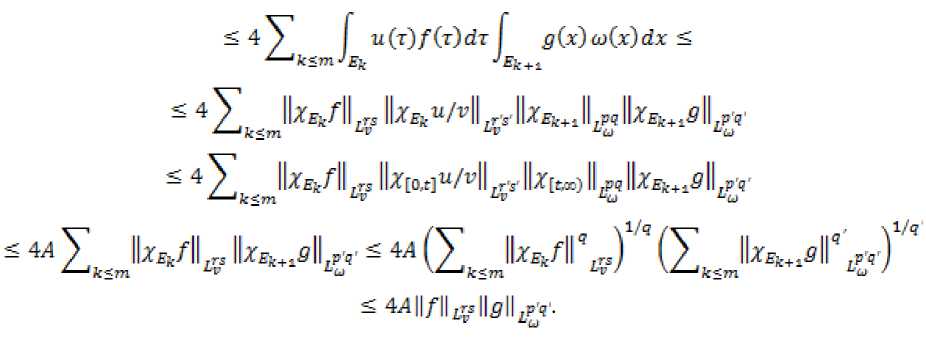
Список литературы Ограниченность интегрального оператора, действующего в весовых пространствах Лоренца
- Bennett C., Sharpley R. Interpolation of Operators. Pure Appl. Math. 129, Academic Press, 1988.
- Sawyer E.T. Weighted Lebesgue and Lorentz norm inequalities for the Hardy operator. // Trans. Amer. Math. Soc. 1984. V. 281. P. 329-337.
- Lomakina E., Stepanov V. On the compactness and approximation numbers of Hardy type integral operators in Lorentz spases.// J. London Math. Soc. (2) 1996. V. 53. P. 369-382.


