Ограниченные ID пучки Эйри: лазерный веер

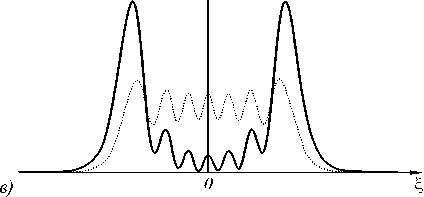
В конце прошлого года появилось сообщение [1], что группа ученых из Флориды с помощью пространственного модулятора света сформировала «усеченный» световой пучок Эйри [2], который при распространении в свободном пространстве приблизительно сохраняет вид на некотором интервале, и траектория распространения основного максимума при этом изгибается. Картина интенсивности распро- странения такого одномерного пучка напоминает радугу [1,2] (см. рис. 1).

Рис. 1. Картина интенсивности распространения идеальной бездифракционной функции Эйри

Бездифракционные световые пучки, наиболее известным из которых является Бесселевый пучок [3,4], характеризуются рядом уникальных свойств, таких как отсутствие дифракционного расплывания на относительно больших расстояниях, повышенная устойчивость к амплитудно-фазовым искажениям. Такие свойства весьма полезны в задачах оптиче- ского неразрушающего контроля, диагностики и манипулирования [5-7].

В отличие от Бесселевых пучков, рассматриваемые здесь одномерные инвариантные пучки Эйри не могут быть представлены как суперпозиция конических волн [2].

В 1979 году в контексте квантовой механики было рассмотрено (1+1)D (одномерное пространственное + временное измерение) решение уравнение Шредингера для свободной частицы в виде функции Эйри [8] и показано, что «пакет Эйри» (также как и плоская волна) не изменяется с течением времени. В этой же работе доказывалось, что других «бездифракционных пакетов» уравнение Шредингера не предполагает.

Однако функции Эйри, экспоненциально спадая при положительных значениях аргумента, при отрицательных значениях демонстрируют осциллирующий характер с плохо затухающей амплитудой [9], то есть являются существенно неограниченными. Поэтому для их физического формирования требуется усечение.

В статье [10] были рассмотрены пучки Эйри с конечной энергией, представляющие собой произведение классической моды Эйри и экспоненциальной функции, а в работе [11] получена обобщенная формула, описывающая параксиальное прохождение Эйри-Гауссовых пучков через оптическую ABCD-систему.

Хотя умножение на гауссовую или экспоненциальную функцию (в последнем случае Фурье-образ пропорционален гауссовой функции) позволяет достаточно просто формировать такие пучки с помощью динамического транспаранта, освещенного лазерным излучением, в обоих случаях формируемые пучки фактически перестают быть инвариантными, хотя приблизительно сохраняют свой вид на некотором интервале.

В данной статье рассматривается иной способ усечения бесконечной моды Эйри – прямоугольной апертурой: от некоторого значения d ₀ в положительной части аргумента (например, значение Ai( x = d₀ =3) практически равно нулю) и до n -го нуля в отрицательной части. Такое «ограниченное» распределение Эйри формируется в поперечном сечении мод резонаторов «шепчущей галереи» [12-15].

В работе [16] было рассмотрено распределение в дальней зоне дифракции ограниченных пучков Эйри, вышедших из такого лазера в свободное пространство. Однако распространение в зоне дифракции Френеля не исследовалось.

В данной статье проводится сравнение степени расходимости трех типов усеченных пучков Эйри: экспоненциальных, гауссовых и просто ограниченных диафрагмой. Численно показано, что в последнем случае осциллирующая структура пучка сохраняется гораздо дольше, чем в двух первых.

y ( x , z ) = Ai

x —

z

2 k

iaz

+— k

I xI z I iaz x exp< a x — 2 — +--

I I 2 k )     2 k

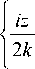
x

z

—

3 I 2 k

? x

1. Теоретические основы

В работе [8] в контексте квантовой механики рассматривается (1+1) D уравнение Шредингера для свободной частицы массы m :

h² d ²

2 m d x ²

- ih— |w ( x , t ) = 0, d t I

Как видно из выражения (6), модифицированная таким образом функция Эйри перестает быть модой, хотя на некотором расстоянии от входной плоскости приблизительно (даже при малых z имеется зависимость от мнимого параметра) сохраняет свою форму.

В статье [11] рассмотрены обобщенные одномерные пучки Эйри-Гаусса:

и решение этого уравнения через функцию Эйри Ai( x ):

i x +8. i

U _i( x _i; K _i, 8 1 , S _i, q _i) = Ai l    ¹ |x I ^K i )

x exp

V ( x , t ) = Ai

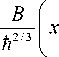
B³t ² )

4 m² )

iB ³ t I B ³ t ²

------1 x--T 2 m h I     6 m

где B >0 – произвольная действительная константа, ℏ – постоянная Планка.

Таким образом, в этой статье показано, что плотность вероятности функции (2) |y( x , t )|² не меняет своей формы в зависимости от времени.

Если переписать уравнение (1) в виде параксиального волнового уравнения распространения в свободном пространстве:

dd |

—2 + 2 ik — |y ( x , z ) = 0, о x        о z I

где волновое число k = 2 л/ % ( % - длина волны) получено формальной заменой m/h = k , то решением уравнения (3) будет функция вида:

у ( x , z ) = Ai

x —

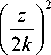
x exp

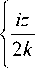
Из выше приведенного выражения видно, что интенсивность функции (4) |y( x , z )|² не меняется при различных значениях z , а лишь смещается пропорционально квадрату этого параметра.

Однако так как функция Эйри является бесконечной, то реализовать ее проблематично. Поэтому в статье [10] рассмотрено действие уравнения (3) на ограниченную по энергии функцию:

y ( x ,0) = Ai ( x ) exp ( ax ) (5) и получено следующее выражение:

x exp iS 1

x +8 I S .³

-ⁱ----¹ + i exp

K i ^{J 3 P}

ikx² |

■AJ,

которые при параксиальном прохождении оптической ABCD - системы принимают следующий вид:

| x-, + 8, i

U ₂( x ₂; k ₂ , 8 2 , S ₂, q ₂) = Ai || x

I ^K 2 )

x exp iS ₂

x ₂ + 8 , i iS 3

—--2 | + —— k2 ) 3

Z 1 \ Z         X —1/2

[ ikx, ² V B | x exp | —- || A + — | ,

1 ² q 2 Л    q i )

где q ₂ =

Aq1 + B

Cq1 + D ’

x

= 8 i

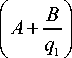
B

2 k K _i

I B i k2 = K11 A + — |, S2 = S1

I      q i )

B

+--,

2 k K 1 K ₂

( S i + S 2 ) .

Используя эти выражения, рассмотрим некоторые частные случаи пучков Эйри.

2. Частные случаи распространения в свободном пространстве

В случае распространения в свободном пространстве на расстояние z матрица [ A , B , C , D ] = [1, z , 0, 1].

i. ^ ( x , z = 0) = Ai( x ).                             (9)

Это классические бесконечные моды Эйри, рассмотренные в [8], которые могут быть получены из (7) при K _i = i, 8 _i = 0, S _i = 0, q _i = ^ . Тогда

z q2 = ~, k2 = i, S2 = —, 82 = 2k

z

2 k

и выражение

(8) принимает следующий вид:

^ ( x , z ) = Ai

I . z

X exp< i —

I 2 k

x —

x—

z

2 k

z

2 k

X

i I z I +— —

3l 2 k J

,

и лишь к смещению исходной функции данное преобразование свести нельзя – появляется зависимость от комплексного аргумента и смещение аргументов у функции Эйри и экспоненты различное.

который полностью соответствует выражению (4).

4. ^ ( x , z

= 0) = Ai ( x ) exp

x ²

2. y ( x , z = 0) = Ai

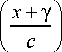
Положив в (7) к 1 = c, 8 1 = Y , S 1 = 0, q 1 = ^ и вы-

z               z I z

писав q., = ^, к = c, S., =----7, 8, = Y------7

^{2        2       2} 2 kc ^{2   2}       2 kc l 2 kc c

,

w

получаем, что:

^ ( x , z ) = Ai

X exp

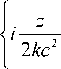
x + Y

c

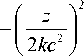
x+Y I z । c l 2 kc2 J

X

i I z I + — ---7

3 ( 2 kc ² J

при смещении и масштабировании исходной функции интенсивность функции (12) остается неизменной по форме, но при распространении смещается на величину, пропорциональную квадрату продольной координаты.

3. y ( x , z = 0) = Ai ( x ) exp ( ax ) ■

Этот частный случай, рассмотренный в [10], можно получить из (7), положив К 1 = 1,

статье

8 1 = 0,

S 1 = — ia ,

q 1 =~ ,

тогда

q 2 = ~ ,

к 2 = 1,

S. = — ia +, 89 = —

²         2 k     ²

z

2 k

z I

— 2 ia + — I , и выражение

(8) принимает следующий вид:

V ( x , z ) =

= Ai

X

z I ²

x l 2 k

iaz

+ —

k

Il iz I exp < a +--X

II 2 k J

z I ²

x l 2 k

iaz

+ —

k

i I z

+—-- ia

3 1 2 k

,

который соответствует выражению (6) за исключе-

Г a нием отсутствия в (6) одного множителя exp I —3

,

который является константой.

Интенсивность функции (13) выглядит следующим образом:

| v( x , z )| 2 = Ai²

x-

z

2 k

iaz

+ —

k

X

IГ -Г z 12

X exp< 2 a x — 2 —

I            1 2 k ^J

J 2 a 3 Г exp

I 3 I

Это вариант пучков Эйри-Гаусса, подробно рассмотренный в работе [11]. Если положить в (7) K 1 = 1, 8 1 = 0, S 1 = 0, q 1 = — ikw ²/2 = — iz ₀

( z ₀–       расстоянии        Релея),        тогда

, „ , . iz c z „ I z I q9 = z — izn, K9 = 1 +, S = —, 89 = — — , и вы-

2            0 2         7      2 9^ 2 I J z0           A.IX             l Z,fV J

ражение (8) принимает следующий вид:

^ ( x , z ) = Ai

I z | x — —

12 k J

1 + iz- z0

. z exp i

^P 2 k

I z I x — —

1 2 k J

1 + z ₀

+

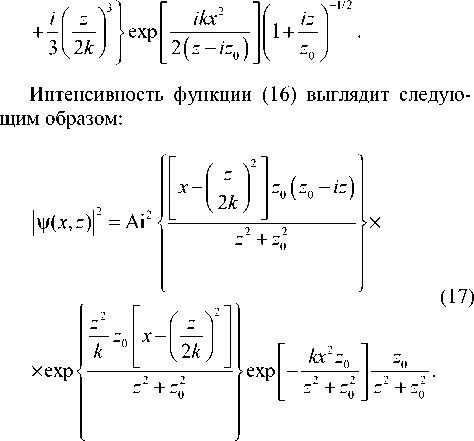
И также нельзя говорить о сохранении формы с точностью до масштаба и смещения.

Стоит отметить, что на расстоянии Релея z = zR пучок уширяется в 2 раза:

I V ^{( x} , ^z = ^z 0 )|² = Ai² 1 2

X exp

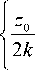
x-

z ₀

2 k

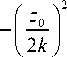
> exp

kx ²

2 z 0

(1 — i ) l x

. 2 z 0

По виду (14) или (17) трудно судить, какой тип усечения исходной функции Эйри меньше влияет на искажение изначальной формы, поэтому позже проведем их численное сравнение.

3. Частные случаи прохождения через тонкую сферическую линзу

При параксиальной фокусировке излучения с помощью тонкой сферической линзы с фокусным расстоянием f матрица [ A , B , C , D ] = [0, f, - 1/f , 0]. 1. ^ ( x ) = Ai( x ), ( к = 1, 8 _j = 0, S _j = 0, q _j = ^ ).

Тогда q 2 = 0, K 2 = 0, S 2 = ^ , 8 2 = ^ и вычислить выражение (8) затруднительно.

Даже если предположить, что распределение в фокальной плоскости линзы соответствует z = ^ , то q2 = ^ , к ₂ = 2, S2 = ^ , 8 2 = ^ и ситуация лучше не становится.

2. у ( x ) = Ai ( x ) exp ( ax ) ( k ₁ = 1, 8 ₁ = 0, S _j =- ia , q j = ~ )•

Здесь для выражения (8) получается аналогичный результат.

Однако в [10] был выписан Фурье-спектр для данного случая в явном виде:

| ф ( Е , f )| 2 = Ai²

kw c, ( w I

—E+ —

2 if    1 2 J

I 2 ( w i x exp< — —

I 3 I 2 J

( f exp

x

-(kw')2 e i

I ² f ²

,

J

т.е. Фурье-спектр представляет собой произведение функции Эйри от комплексного аргумента и гауссовой функции, радиус которой w f =X f ^ ww обратно про-

порционален радиусу исходного гауссового пучка.

Интенсивность при f = z ₀ ( w z 0 = w ):

I ф ( Е , f = z 0 ) 2 = Ai²

x exp

2 ( w I

3 1 T J

^- i ^{E +}

> exp

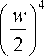
- 2 E ²

ф ( Е ) = exp ( - a E ² ) exp 3 ( E 3 - 3 a A ia ³) ,

( 2 л³ I

| Ф( ^)| = exp ( - 2 a E ) exp I — I ,               (20)

т.е. в дальней зоне дифракции такой пучок будет всегда сходиться к гауссовому пучку, эффективный радиус которого обратно пропорционален корню квадратному от параметра экспоненциальной функции a .

( x¹

3. y ( x ) = Ai ( x ) exp I-- 2

I w

( K j = 1, 8 j = 0,   S j = 0,

q _j = - ikw ²/2 = - iz ₀).

Тогда q ₂ =- — , к ₂ = —, S ₂ =- 'z , 8 2 = у ⁷² .., ^z 0          ^z 0           ^{2 k}       ( 2 k )

выражение (8) принимает следующий вид:

и

Ф ( Е , f ) = Ai | E+I^ if    1 2 k.

x

x exp ^-

iz 0 z 0 E + ( z 0 2 k if" 1 2 k.

z

z

2 k

(- kz E ² i( z Y/²

x exp --0y- —

I 2 f ² JI if J

,

| ф( ^ , f )| 2 = Ai²

j ( Y 3I 2 k J

^ x

7          7   \ z 0 E J z0

iV 1 2 k J

I 2 ( z ₀ | x exp — —

I 3 I 2 k J

x

I      ( - kE2

exp 0

I f²

,

или, через радиус исходной гауссовой функции w :

4. Численное сравнение распространения усеченных пучков Эйри в свободном пространстве

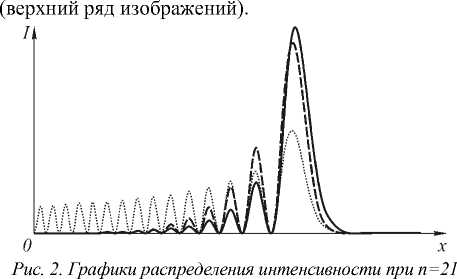
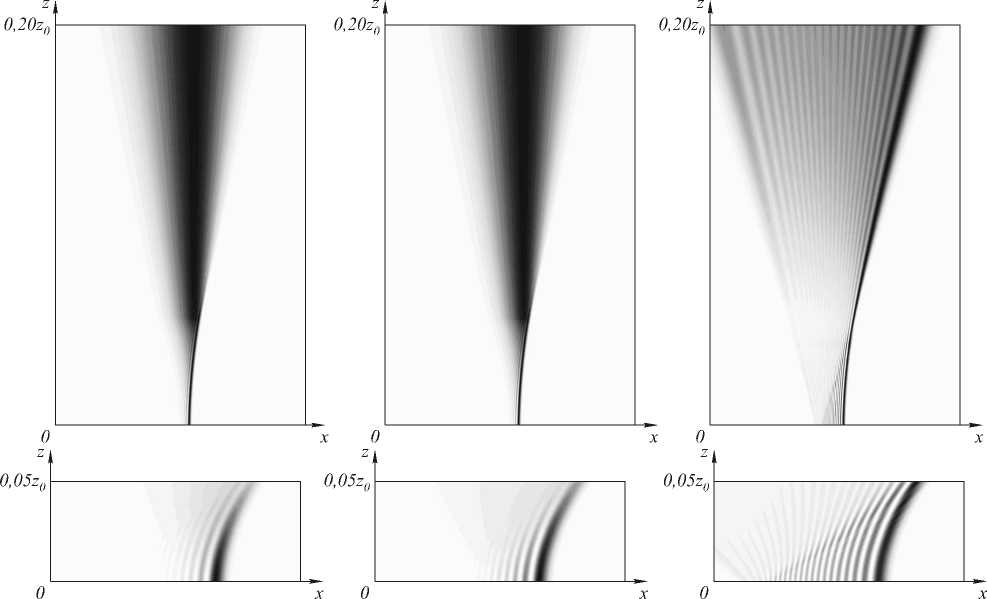
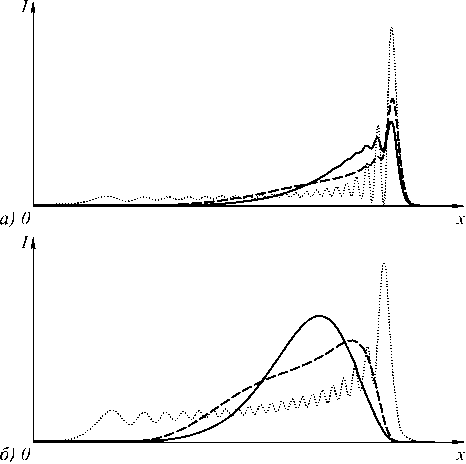
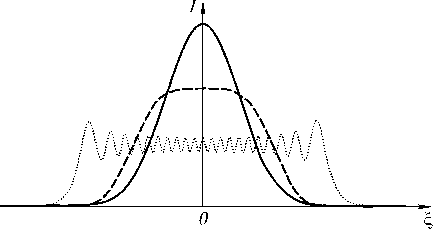
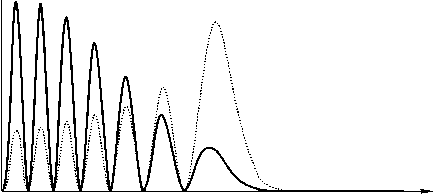
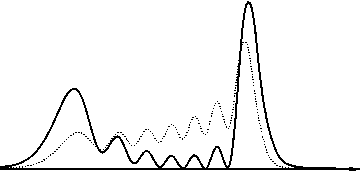
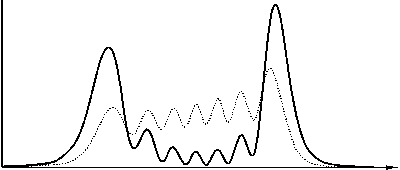
В данном разделе проведено сравнение степени расходимости усеченных пучков Эйри при распространении в свободном пространстве. Среди рассмотренных – экспоненциальные (13), гауссовые (15) и ограниченные пучки Эйри ( a = b =0):

V.(x,z = 0) = (Ai(x),Yn 5x

В проведенных численных экспериментах выполнялось преобразование Френеля и Фурье от входных функций:

fn (x) = Vn II, (26) I c J масштабно приведенных к единичному интервалу: [0, 1 мм].

В расчетах также использовались следующие параметры: длина волны %=633 мкм, расстояние z₀= kR2/2, где R=0,5 мм (т.е. рассматривается половина входной апертуры), параметры a и b выбирались такими, чтобы exp( a у _n) = 0,0j, exp(-b у n) = 0,0 j.

На рис. 2 приведены интенсивности f_n (x) ² при n=21 экспоненциального (сплошная линия), гауссо-вого (пунктирная линия) и ограниченного пучков Эйри (точечная линия) на входе (при z=0), отнорми-рованные по энергии.

На рис. 3 показано распространение соответствующих пучков в свободном пространстве: картина распределения интенсивности на участке от z=0 до z=0,05z₀= 62 мм (нижний ряд изображений) и картина распределения структуры интенсивности (т.е. максимумы в каждом сечении приводились к одной

величине) на отрезке от z=0 до z=0,2z₀=248 мм

экспоненциального (сплошная линия), гауссового (пунктирная линия) и ограниченного пучков Эйри (точечная линия) на входе (при z=0), отнормированные по энергии

Из рис. 2 хорошо видно, что ограниченный пучок Эйри (25) значительно лучше аппроксимирует структуру идеальной функции (она «ближе к радуге») и сохраняет осциллирующий характер структуры до бесконечности (что подтверждает спектральное распределение, приведенное на рис. 4).

На рис. 4 показаны распределения интенсивности в сечениях соответствующих пучков при значениях z=0,05z0 и z=0,1z0, откуда хорошо видно, что ограниченный пучок также значительно меньше подвержен дифракции, чем другие типы усеченных пучков. Эйри-Гауссовый пучок держится несколько дольше экспоненциального, но все равно очень быстро вырождается по сравнению с ограниченным.

На рис. 5 показаны интенсивности Фурье-спектра |ф(^, f)|2усеченных пучков Эйри при f = z0/4. Из рисунка видно, что спектр экспоненциального пучка Эйри, как и следует из формулы (20), близок к гауссовой функции, а спектр Эйри-Гауссового пучка имеет более интересный вид – распределение с плоской верхушкой (так называемое «флэт-топ»), которое, например, может описываться супергауссовой функцией. Достичь такого распределения [19] часто бывает полезно в различных задачах, таких как улучшение качества печати, микролитография, обработка материалов, оптическое манипулирование. Фурье-спектр от ограниченного пучка Эйри (25) полностью совпадает с результатами, полученными в работе [16], и аппроксимирует прямоугольник.

Интересно отметить, что спектры экспоненциального и Эйри-Гауссового пучков с увеличением индекса n не изменяют своей формы, как это и следует из формул (20) и (23), а спектр ограниченного начинает приближаться к прямоугольной форме (амплитуда осцилляций уменьшается).

Разумеется, полученные результаты связаны с иным способом усечения бесконечной функции Эйри – не подавлением осциллирующей части, а обрезанием. Можно, конечно, изменить параметры a и b так, чтобы оставалось большее количество неподавленных осцилляций, но за это придется платить либо увеличением входной апертуры, либо большей плотностью сигнала на той же апертуре.

a)                                              б)                                            в)

Рис. 3. Распространение экспоненциального (а), гауссового (б) и ограниченного (в) пучков Эйри в свободном пространстве: картина интенсивности на расстояние до z=0,05z0 (нижний ряд) и картина структуры до z=0,2z0 (верхний ряд)

Рис. 4. Графики распределения интенсивности при n=21 в сечениях экспоненциального (сплошная линия), гауссового (пунктирная линия) и ограниченного пучков Эйри (точечная линия) при значениях z=0,05z0 (a) и z=0,1z0 (б)

Рассмотрим далее, как влияет еще большее усиление осциллирующей части в ограниченном пучке на его свойства. В качестве входной функции будем рассматривать ограниченно-гауссовую функцию:

gn⁽x) = fn (x) ^exp [^-b⁽x - x0⁾²] , x0 ^{e [0,1}L ⁽²⁷⁾ где fn (x) - ограниченная n нулями и приведенная к единичному отрезку функция Эйри из (26).

Ниже приводятся сравнительные результаты моделирования распространения ограниченной функ- ции (25) и (27) при n=7 и следующих параметрах гауссовой функции: b=4,6; x0=0.

Рис. 5. Графики распределения интенсивности при n=21 Фурье-спектра экспоненциального (сплошная линия), гауссового (пунктирная линия) и ограниченного пучков Эйри (точечная линия) при f = z₀ / 4

На рис. 6 показана интенсивность на входе, на рис. 7 - сравнительная картина распространения в свободном пространстве, на рис. 8 - распределение интенсивности соответствующих пучков на расстоянии z=0,2z₀ и z=0,5zо и в Фурье-плоскости.

Ц

а)

б)

Рис. 7. Распространение ограниченного (а) и ограниченно-гауссового (б) пучков Эйри в свободном пространстве: картина интенсивности на расстояние до z=0,5z0 (левый столбец) и картина структуры до z=z0 (правый ряд)

Рис. 6. Графики распределения интенсивности ограниченного (точечная линия) и ограниченно-гауссового (сплошная линия) пучка Эйри при n=7 на входе (при z=0)

a) О I,

б) О

Рис. 8. Графики распределения интенсивности при n=7 в сечениях ограниченного (точечная линия) и ограниченно-гауссового (сплошная линия) пучков Эйри при значениях z=0,2z0 (a), z=0,5z0 (б) и в Фурье-плоскости (в)

Из приведенных результатов видно, что ограни-ченно-гауссовый пучок Эйри позволяет формировать распределение, бесконечно долго сохраняющее концентрацию энергии в узком боковом лепестке.

Заключение

В данной работе численно рассмотрено распространение различных типов усеченных пучков Эйри в свободном пространстве.

Показано, что ограниченный пучок, в частности, формируемый в поперечном сечении мод резонаторов «шепчущей галереи», значительно меньше подвержен дифракции, чем другие типы усеченных пучков . Эйри-Гауссовый пучок сохраняет свое распределение несколько дольше экспоненциального, но все равно очень быстро вырождается по сравнению с ограниченным.

Кроме того, ограниченный пучок Эйри значительно лучше аппроксимирует структуру идеальной функции («ближе к радуге») и сохраняет осциллирующий характер структуры до бесконечности, демонстрируя веерный характер.

Показано, что спектр экспоненциального пучка Эйри, как и следует из аналитических выкладок работы [10], является гауссовой функцией, а спектр Эйри-Гауссового пучка имеет распределение с плоской верхушкой, которое может быть полезно в таких задачах, как улучшение качества печати, микролитография, обработка материалов, оптическое манипулирование. При этом спектр ограниченного пучка Эйри приближается к прямоугольной форме при большом количестве учтенных в начальном распределении осцилляций.

Полученные результаты связаны с иным способом усечения бесконечной функции Эйри – не подавлением осциллирующей части, а обрезанием. При этом, если искусственно поднять энергию осцилляций, то с помощью такого ограниченно-гаус-сового пучка Эйри можно формировать распределение, бесконечно долго сохраняющее концентрацию энергии в узком боковом лепестке.

Работа выполнена при финансовой поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-Sa-06), грантов РФФИ №№ 07-07-97600, 08-07-99007 и гранта Президента РФ № НШ-3086.2008.9.