Охлаждение горячего газа твёрдыми охладителями

Газ как рабочее тело применяется в различных областях техники. Одной из таких областей является использование газа для заполнения различного рода понтонов при подводных работах, автомобильных подушек безопасности, плавающих платформ разного назначения и т. п. [1]. Применение газобаллонных систем для этих целей требует наличия баллонов с сжатым газом высокого давления, что не всегда оправданно с точки зрения габаритов и массы.

С этой точки зрения более выгодно использовать твёрдое топливо, продукты сгорания которого можно использовать в вышеуказанных системах. Однако для этого необходимо снизить температуру газа до 350...450 К. Одним из методов охлаждения горячего газа является пропускание его через слой твёрдого охладителя, разлагающегося с поглощением тепла. В качестве охладителей применяются составы, продукты разложения которых не содержат агрессивных газов, например, углекислый аммоний.

На рис. 1 изображена принципиальная схема низкотемпературного газогенератора (НТГТ). Продукты сгорания топлива из камеры сгорания (КС) поступают в камеру охлаждения (КО), в которой находится твёрдый охладитель в виде гранул.

КС

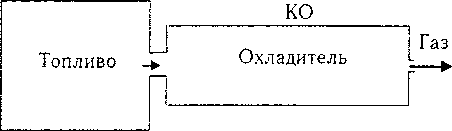
Рис. 1. Принципиальная схема НТГГ

Температура горения топлива составляет 1600...2000 К. Рабочие процессы в КС описываются обычно нульмерной математической моделью, поскольку температура и давление по длине КС меняется незначительно. В КО температура меняется от температуры горения топлива в среднем до 400 К. В широком диапазоне изменяются также плотность и давление. Кроме того, как показывают экспериментальные исследования [2], скорость разложения охладителя сильно зависит от температуры газа и существенно изменяется по длине КО. Обычно подобные аппараты обладают осевой симметрией, поэтому для описания процессов гидродинамики и тепло- и массообмена применяются одномерные математические модели. Применение двумерных и трёхмерных математических моделей требует описания движения газа в каналах сложной формы, образованных разлагающимися гранулами. А поскольку заполнение КО гранулами производится засыпкой, расположение гранул и форма каналов имеют случайный характер. Кроме того, нужно описывать движение каждой гранулы. Количество гранул в КО составляет от нескольких сотен до нескольких тысяч. Подобные задачи в настоящее время практически не реализуемы даже на суперкомпьютерах. Поэтому движение газа через слой гранул целесообразно описывать как течение через пористый слой некоторой начальной пористости. По данным [3] при свободной засыпке средняя пористость находится в диапазоне 0,32...0,39.

Газовая смесь в КО состоит из неконденси-рующихся продуктов сгорания топлива (НК газы

ПСТ), таких как, например, углекислый газ и т. п., неконденсирующихся продуктов разложения охладителя (НК газы ПРО), таких как углекислый газ, аммиак и т.п., и водяного пара. Состояние НК газов в КС и КО и пара в КС подчиняется уравнению состояния идеального газа. Состояние водя-

ного пара в КО определяется согласно [4].

Рабочие процессы в КС описываются дующей системой уравнений:

^Ркс^кс „        п .

»         Г Т Т Т КС 7

ат

сле-

do V с Т

WMKC KC VKC KC

Рп=р(/>пЛ);                     (13)

S = S_oe; R = £ Rjg, ; с^^c_vig_f ; i= т, х, а.

Здесь J_m - поток массы продуктов разложения охладителя в КО; J_{m 6} - поток массы /-го компонента; х - продольная координата; г - радиальная координата; а - коэффициент температуропроводности; 77_экв - эквивалентный периметр гранул; Q_m - сток тепла из-за разложения охладителя; ^ - коэффициент гидравлического сопротивле

dx ^РксКп,кс^кс dx ^РксКт.кс^с dx

p^u^h_TF_T G_KC/?_KC Оке,

Р,"ЛР„ ^ксКп.кс’

Pt^T^T (1 Рп ) ^kcS't.kc ’

С О У ^«.кс <_т __т \р .

W ^      ^КС \ КС И-,КС / W,KC ’

Ркс ~ PkC^kcTrC ’

Т^кс ~ ^т8т + ^п8п "*" ^aga ’ cvkc —         ‘'vnKn ^vaSa •

Здесь р - плотность; G - расход; р - давление; Т - температура; h - энтальпия; F— площадь поверхности; V - объём; Q - тепловой поток; R - газовая постоянная; а — коэффициент теплоотдачи; c_v - удельная теплоёмкость при постоянном объёме; с - удельная теплоёмкость; g — массовая доля компонента газовой смеси; т - время; р_п - массовая доля водяного пара в продуктах

сгорания топлива; индексы: w - стенка; т - топли

во; а - воздух; кс - камера сгорания.

Движение газа в КО описывается следующей системой уравнений:

сФ гт г --1--= F ,

Эх Эх

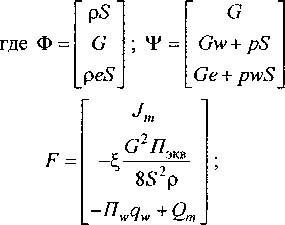
(Ю)

(И)

ния; q_w - плотность теплового потока; 8 - пористость; 5₀ - площадь сечения КО без охладителя;

w - скорость; индексы: х - охладитель.

Начальные и граничные условия системы уравнений (1)—(5), (8)—(11) записываются следующим образом:

Р_Ю^=Р^ ^(0) = ^; T_w(O) = T_o; g,_KC(0) = 0. (14) р(О,х) = р_о;Г(О,х) = Г_о;С(О,х) = О;

7w(O,r)=7o;g,(O,x) = O.

На входе в КО граничные условия задаются в виде:

т - ^к рЧ^УЧ^ .

£-1 кскс Л-1 ркс(т) 2    ’

Ркс (^т) = 7(т,0) + p(t,0)w² (т,0) ;

Кт (^>®) ^— Кт,кс (^)’ Кп (^’ 9) ~ Кп,кс (^)’ g_x(i,0) = 0,

где к - показатель адиабаты. На выходе из КО граничное условие записывается следующим образом:

Рн при —-

Р

к

( 2

1^ + 1}

G(T,Z) = pS "^рр

при ^< Р

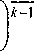
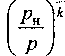
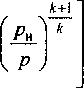
G(r,/) = pS--- J—PP- (19) \ / ^Нвь1хц+1; Чк+г

Здесь р - давление на выходе из КО,

р_н - давление у потребителя; и - коэффициент

расхода; 5ВЫХ - площадь выходного отверстия. Для уравнения теплопроводности (И) задаются граничные условия III рода.

Уравнения (I)—(5) решаются методом Рунге-Кутта 4-го порядка [5]. Для решения уравнений (8)—(11) применяется метод конечных разностей. Уравнения (8) аппроксимируются неявной разностной схемой на равномерной разностной сетке:

Теплоэнергетика ф^+1 _фт Ц7^+^ __Шт+^

-^-----«_ + _Л -----Д±. = _F^ n=2...N. (20)

Ат         Ах

Здесь и - номер узла разностной сетки по длине КО; т - номер момента времени; Ах, Ат -шаги разностной схемы по координате х и времени соответственно. Векторы Ф"^+х ^^ ,F^^+X раскладываются в ряд Тейлора с сохранением первых членов ряда:

ся к трёхточечному разностному уравнению. Решение разностного уравнения выполняется трёхточечной скалярной прогонкой [6].

Результаты расчёта представлены на рис. 2-4.

т+1 п

фт+1 = фт+1

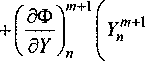
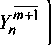
_ ш^+1 т л

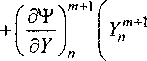
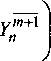
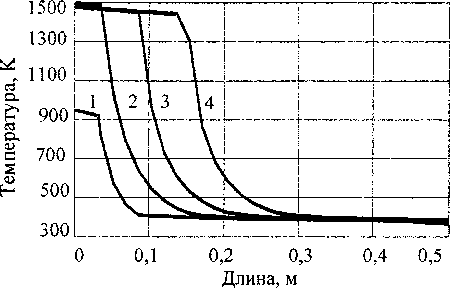
Рис. 2. Изменение температуры по длине КО: 1 - т =0,02 с; 2-т =0,2 с; 3 - т =2,0 с; 4-т=4,0 с

V3YJn (         )

Y* = |p,T,G|.

В результате разностное уравнение (20) приводится к виду

Ajr^X-B_n^=C_n,n=-2...N,      (21)

где А и В - матрицы 3 х 3 , С - вектор размерности 3;

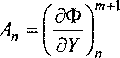
A /^Tr\W + 1 , _ Ат ( ЭТ )

Дт[ Эц/

Axl ЭУ

Лт®

W„

Ах <5^ Л-1

+AnYrX-Bn_xY^\

+ AtF”+1

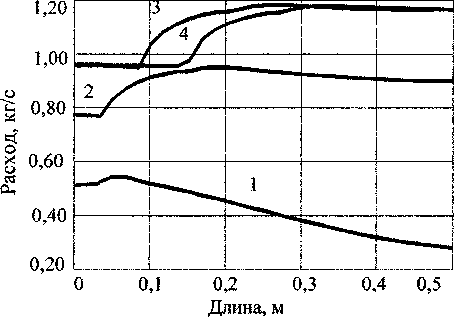
Рис. 3. Изменение расхода по длине КО

Индекс 1н + 1 означает параметр на предыдущей итерации ( т +1 )-го слоя по времени.

Уравнения (10) аппроксимируются неявной разностной схемой

(<М+!СЧ<

Ат              Ах

ац:1. та

из которой находятся массовые доли компонентов газовой смеси.

Граничные условия (16), (17) преобразуются к виду

AY^¹ = С,,                         (23)

где А_х - матрица 2x3, С, - вектор размерности 2.

Граничное условие (19) преобразуется к виду

B_NY^^X=C_N,                    (24)

где B_N - вектор размерности 3, C_N - скаляр.

Краевая задача (21), (23), (24) решается методом ортогональной прогонки [6, 7].

Уравнение теплопроводности (И) аппроксимируется неявной разностной схемой и приводит

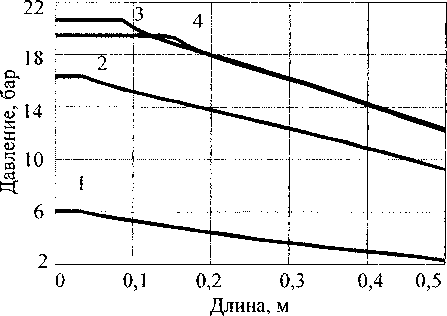
Рис. 4. Изменение давления по длине КО

На рис. 2 показано изменение температуры по длине КО в различные моменты времени. На рис. 3 показано изменение расхода по длине КО, а на рис. 4 - изменение давления по длине КО. Температура продуктов сгорания на входе в КО составляет 1500 К.

С течением времени из-за разложения гранул фронт горячего газа перемещается в глубь КО. Однако температура на выходе из КО находится на уровне 400 К. Изменение расхода и давления на входе в КО связано с горением топлива в КС и вследствие этого изменением давления в КС. Истечение из КС в КО происходит при критическом перепаде давления, поэтому процессы, происходящие в КО, не влияют на характер изменения параметров в КС.

Как следует из рис. 4, слой гранул представляет довольно большое гидравлическое сопротивление, вследствие чего изменение давления по длине КО составляет от 4 до 8 бар.