Оконтуривание фазы и визуализация точек фазовой сингулярности световых полей с помощью кольцевого преобразования радона

Преобразование Радона (ПР) известно с 1917 года. Оно широко применяется в обработке изображений, томографии, геодезии, медицине [1-5]. Двумерное преобразование Радона ставит в соответствие функции двух переменных средние значения этой функции на всевозможных прямых линиях, лежащих в плоскости:

R [ f I P 6 ) = jj f ( x, У Ж P - x cos ^ — У sin 0 ) dxdy ’ ⁽¹⁾ R ²

где ( p, 0) — полярные координаты, описывающие прямую: р - расстояние от начала координат до прямой, 0 - угол наклона прямой к оси Ox .

Обобщением ПР является преобразование Хоу [6], которое ставит в соответствие функции средние значения этой функции на всевозможных линиях (необязательно прямых). Преобразование Хоу также имеет достаточно много применений. Например, оно применяется для компьютерной обработки видеоизображений листьев растений с целью определения площади листовой поверхности [7]. В этой работе функции ставятся в соответствие интегралы по кривым, имеющим форму эллипса. Существуют также медицинские приложения преобразования Хоу. В работе [8] оно используется для выделения и подавления изображений ребер на флюорограммах. В работе [9] преобразование Хоу применяется для сегментации полутоновых изображений.

В данной статье будет рассматриваться частный случай преобразования Хоу – преобразование, ставящее в соответствие функции двух переменных интегралы этой функции по окружностям в плоскости.

В [10] введено некоторое обобщение преобразования Радона – усреднение по сферам. Усреднение по сферам используется в радарах с синтезированной апертурой (SAR) и в акустической навигации (SONAR – sound navigation and ranging).

Для двумерного случая в [11, 12] приведены теоремы о взаимно-однозначном соответствии между функцией двух переменных и всеми интегралами по окружностям, лежащими в плоскости. То есть в [11, 12] введено в рассмотрение кольцевое преобразование Радона (КПР), хотя оно там так и не называется. Заметим, что КПР можно определить разными спо- собами, потому что усреднение по всем окружностям в плоскости является переопределенным, так как набор всех окружностей имеет размерность три, что больше размерности двумерного пространства. В [13] рассматривается КПР как усреднение по всем окружностям, имеющим одну общую точку в центре координат, в [12] КПР определено как среднее по окружностям разного радиуса, центры которых лежат на некоторой фиксированной окружности с центром в начале координат. В [14, 15] рассматривается КПР как среднее по всем окружностям фиксированного радиуса на плоскости.

В отличие от КПР, определенного в [12, 13], КПР, определенное в [14, 15], является сверткой:

К _у ( 5 , П ) = jj f ( x , У ) ж [ Y -л[ ( 5 - x ) 2 + ( п — У ) 21 dxdy , ⁽²⁾ R ²          ^                           ^

а потому может быть реализовано оптически с помощью Фурье-коррелятора.

На этом свойстве основано оптическое выполнение традиционного преобразования Радона [16].

В данной работе будут рассмотрены еще два применения КПР – оконтуривание фазы и визуализация точек фазовой сингулярности световых полей.

1.    Оконтуривание фазы световых полей 1.1.    Визуализация фазовых неоднородностей светового поля

Многие интересные для микроскопии объекты обладают высокой прозрачностью и поэтому совсем или почти совсем не поглощают свет (например, бесцветные бактерии). При прохождении света через такой объект основным эффектом будет появление сдвига фазы, величина которого различна в разных точках. Подобный эффект, конечно, нельзя наблюдать с помощью обычного микроскопа и приемника, реагирующего на интенсивность света.

Визуализация фазовых неоднородностей осуществляется с помощью Фурье-коррелятора при размещении в частотной плоскости фазового фильтра Цернике (такое устройство называют теневым прибором [17]). Пусть на входе имеется фазовое световое поле со слабой модуляцией фазы (| ^ ( x ) <<  1):

f (x) = exp[z^(x)]

Тогда (3) можно разложить в ряд с точностью до квадратичного члена:

exp [ i ф ( x ) ] « 1 + i ф ( x ) .

d 2               d 2

— g ( x , у ) = —r Jf G ( fe , п ) exp [ i ( x ^ + у п ) ] dd = д x ²           д x ² R 2

В частотной плоскости коррелятора получим комплексную амплитуду

3 { exp ^[ i ^ ( x ^)]} = 5fe ) + i Ф ( ^ ) ,                   (5)

где ф ( ^ ) - Фурье-образ ф ( x ) .

Фильтр Цернике имеет пропускание вида:

= - JJ fe ² G ( fe , п ) exp [ i ( x fe + У п ) ] dd =

R ²

= -3

-I

¹ fe ² G ( fe п ) }

Подставляя (12) в (11), получим:

^- i , fe <А

г I д ² f д ² f E = f - i a l +

( д x ²     д у ²

.

1 fe >А

которое можно реализовать с помощью прозрачной пластины с показателем преломления n , имеющей ступеньку высотой z :

Если объектная функция – фазовая, т.е. f ⁽ x , у ) = ехр ф x , у ^)] ,

то ее вторая производная имеет вид:

X

4 ( n - 1 ) ’

где X - длина волны света. Диаметр ступеньки 2 А равен ширине функции импульсного отклика линзы коррелятора. С учетом (5) и (6) на выходе коррелятора получим комплексную амплитуду вида

³ { ³ { ^exp M x ^)]} H ^} = (8) = 3 { i S ( fe ) + i ф ( ^ )} = i [ 1 + ф ( и ) ]

и интенсивность

I ( fe ) = 1 + 2 ф ( и ) + ф ² ( и ) « 1 + 2 ф ( и ) .            (9)

Из (9) видно, что распределение интенсивности света на выходе коррелятора с фильтром Цернике пропорционально фазе исходного светового поля, т.е. модуляция интенсивности на изображении зависит от фазы изображения, а это и есть эффект визуализации фазы. Однако при больших значениях фазовой функции ф ( и ) приближенное равенство (9) будет нарушено и интенсивность на выходе коррелятора будет зависеть от фазы светового поля нелинейно.

1.2. Визуализация фазового объекта с помощью малой дефокусировки

Для малой дефокусировки можно либо сдвинуть выходную плоскость Фурье-коррелятора E ( x , у ) , либо использовать фильтр H ( fe , п ) в виде слабой параболической линзы:

H ( fe , п ) = exp^ afe ² + п ² ) ] ,                    (10)

где а <<  1.

Тогда для Фурье-коррелятора получим:

E = 3^{- 1} { 3 { f } ■ H } = 3^{- 1} { 3 { f } ■ exp ( i a r ² )} «

«3 ¹ { з { f } • (1 + i a r ² )} =

= 3^{- 1} { 3 { f }} + i a 3^{- 1} { 3 { f } ■ r ² } =

= f + i a 3^{- 1} {3 { f } • ( * ² + п ² )} .                 (11)

Если g ( x , у ) - Фурье-прообраз G ( fe , п ) , то

д ² ф

еЦ = fi е^ ф д x ² д x ²

д x

Тогда

E = exp ( i ф ) +

+ а expp

д ф 1 д x J

.

5- ? +^ + i (г x¹ ау² J

= ехр ( ф ) ■< 1 + a l

д ² ф д ² ф д x ² д у ²

+ i a

д ф 1 I д ф 1

—- I +1 — 1 д x J l д у J

.

22 д ф 1 I д ф 1 — I +l — I д x J   l д у J

+

Интенсивность после дефокусировки иметь следующий вид:

i =1 E ² =

+ a

2 Рф l д x

.    | д ² ф д ² ф

1 + al+

(д x ² д у ²

1 +!^Ф|«

J (д у J

| д ² ф  д ² ф

1 + 2 a | —+

( д x ²    д у ²

+

будет

Из выражения (17) видно, что интенсивность после дефокусировки будет пропорциональна лапласиану от фазы. В точках перегиба вторая производная будет равна нулю, а в точках экстремума фазы максимальна.

Преимущество метода дефокусировки перед фильтром Цернике в том, что не требуется предположения о «слабости» фазового объекта ( ф <<  1) и вместо фильтра Цернике можно использовать обычную сферическую «слабую» (длиннофокусную) линзу или просто сместить выходную плоскость коррелятора.

Недостаток метода дефокусировки в том, что интенсивность на выходе коррелятора пропорцио-

нальна не самой фазовой функции, а ее вторым производным.

1.3. Оконтуривание фазы светового поля с помощью кольцевого преобразования Радона Пусть объектная функция фазовая:

f ( x , y ) = exp [ z ^ ( x , y ) ] .                          (18)

Рассмотрим ее КПР-образ:

Аналогично, d f = if 0^ d y d y

Далее вычислим ее частные производные второго порядка.

1 ^{2 п}

R y ( 5 , n ) = — J f ( 5 + / cos t , n + / sin t> .   (19)

^{2 n} 0

В подынтегральном выражении стоит значение функции в точке, отстоящей от точки ( 5 , n ) на расстоянии / в направлении p = ( cos t ,sin t ) . Разложим функцию f ( x , y ) в ряд Тейлора в окрестности точки ( 5 , n ) по направлению p :

02 f = i \0f_ 0Ф + f д 2Ф | = дx2 |dx дx    9x2 J

22              2            2

. _\ дф 1 .6 ф , . д ф \ дф 1 = i if — I + f —v = f i —v -1 I

(д x J     д x²         д x² (д x J

^{д 2 f} = _{f i} ^д 2 Ф -| ^д Ф J ² д y      д y (д y J

f ( 5 + / cos t , n + / sin t ) =

=[ f + / ^f + / 2 S+-1

L ^    d P ²   L

⁵ , ⁿ

Подставляя (27)-(28) в (24), получим:

R _Y( § , n ) * f ( ^ , n ) ^x

.

X

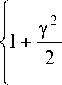
. д ² Ф д x ²

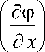
. д ² ф

+ ¹2

д y ²

-

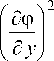
^ , n J

Выражения для первой и второй производных по направлению p имеют следующий вид:

д f       д f   . д f

= cos t — + sin t — , д p      д x д y

L Y ²

= exp [ i ф ( ^ , n ) ] - S 1 — 2"

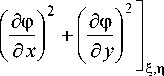
д ² f 2 f ² f ■ 2 д ² f ■ . д ² f ™ —V = cos ² 1— + sin ² 1— + sin2 t—— . (22) д p д x ² д y ² д x д y

При небольших значениях / <<  1 в выражении (20) будем учитывать только первые три слагаемых. Подставляя (21) и (22) в (20), получим:

f ( 5 + / cos t , n + / sin t ) =

/ 2 а^ ф а^ ф 2 L9 x ² д y ²

Умножая R _/ ( 5,n ) на комплексно-сопряженное значение и пренебрегая слагаемыми порядка / ⁴,

получим:

г I       9 f    -5 f 1

= f + / I cos t — + sin t— I

L (     ⁵ x      д y JJ

⁵ , ⁿ

+

| R / ( 5 , n ) ² = 1 - / ²

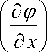
I д ф 1 + I I

( д y J

5 , n

2    2 0 2 f • 2 d 2 f . „ 0 2 f

+/ ² cos ² 1 —— + sin ² 1 —— + sin2 1----

_      d x'         d y 2        d x 0 y

= 1 - / ²1 ^ ф ( 5 , n ) 2 .

.

- 5n

При интегрировании по t от 0 до 2 п в уравнении (19) слагаемые, содержащие cos t , sin t , sin 2 t , обратятся в нуль, поэтому (19) примет вид:

i \      1

R/ ^{( 5 ,} n )~— ² n f ^{+ n} Y

2.K

. 2 MV .S f I д x ²

д y

^J 5 , n

_     / ² 1 d ² f d ² f

= f +    ¹   T +-- T

² | d x ²    d y ²

.

^J 5 , n

Вычислим частные производные первого поряд-

ка от фазовой функции (18):

| f = 7- exp M x , y ^)] = д x д x

= . ^ехр ^{[ ф ( x} , y ^{) ] 9 ф} = if д x д x

.

Из выражения (30) видно, что R _/ ( 5 , n ) находится в линейной зависимости с квадратом модуля градиента фазы объектной функции, и принимает наибольшее значение в тех точках, где фазовая функция постоянна. Таким образом, КПР может быть использовано для оконтуривания фазы.

На рис. 1(а) изображена некоторая фазовая функция (128x128 отсчетов). Для численного эксперимента была выбрана кусочно-постоянная функция с фазой 0 (белые квадраты) и п (черные квадраты). На рис. 1(б) показан модуль КПР со значением параметра КПР / = 1 отсчет.

Из рис. 1(б) видно, что действительно при малых значениях параметра КПР / интенсивность КПР-образа минимальна в местах резкого изменения фазы входной функции.

Преимущество КПР-метода по сравнению с методом дефокусировки в том, что выходная интен-

сивность зависит от первых, а не вторых производных от фазовой функции.

а)        б)

Рис. 1. Оконтуривание фазы: входная фаза (черный цвет - п , белый цвет - 0 ) (а), интенсивность

КПР-образа при у = 1

(белый цвет – максимальная интенсивность, черный цвет – минимальная интенсивность) (б)

Недостатком КПР-метода является то, что применяется энергетически неэффективный амплитудный фильтр.

В тех областях, где фаза резко меняется, рассчитывался контраст по следующей формуле:

C =

max min

I max + I min

теория волн с фазовыми сингулярностями получила дальнейшее развитие. В [20] показано, что волна, имеющая «вихри», является одним из возможных решений скалярного волнового уравнения.

В простейшем случае выражение для оптического «вихря» имеет вид r ■ ехр(т ф ) , где n - порядок, положительный для правосторонних «вихрей» и отрицательный для левосторонних [22].

Примером световых полей с «вихрями» являются широко известные лазерные пучки Гаусса-Лагерра. Благодаря винтообразной структуре волновых фронтов, эти пучки обладают свойством передавать угловой момент поля в свободном пространстве, что может использоваться для создания «ловушек» микрочастиц и оптических «гаечных ключей» [23-26].В этом разделе рассматривается применение КПР для анализа световых полей, проверки их на наличие «вихрей», определения их расположения и порядка.

Пусть объектная функция f ( x , у ) представляет собой композицию K «вихрей», т.е. спиралевидных фаз порядков n ₁, n ₂ ,..., n_K с точками фазовой сингу^лярн^{ости (} x_b У 1 ) ⁽ x 2 , у 2 ), ..., ⁽ x K , У к ) :

I = К ( §п ) 2 ,

K I f ( x , у ⁾⁼ П exp l in k arctg k = 1      I

У ^- У к ^{x -} x k .

где I и I – минимальная и максимальная ин-min max тенсивность в области перепада фазы.

Была исследована зависимость контраста от величины фазового скачка (от 0 до 360⁰) (рис. 2). Из рис. 2 видно, что контраст изображения максимален при разности фаз в двух соседних точках, близкой к п .

Тогда функция f ( x , у ) - фазовая с фазой ф ( x , у ) :

ф ( x , У ) = Е n k arctg y y k к = 1          ^{x -} x k

.

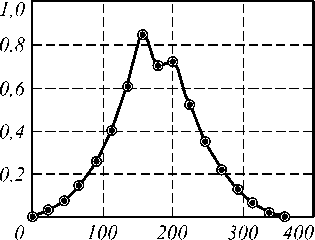
Рис. 2. Зависимость контраста от величины фазового скачка

Для получения выражения для интенсивности на выходе воспользуемся формулой (30). Для этого получим частные производные фазы (34).

I                                                                         ¹

^д ф K I„ 1,1 у ^- Ук I        У ^- Ук

^Е1 n^{k 1} + l          I                \2

^д x      к = 1 | I ^{x -} x k )       ⁽ x ^- x k )

^^^^^^в

K

Е

к = 1

nk

У ^- У к

^{( x -} x k ^{) 2 +(} У ^- У к ^{) 2}

д ф K I

⁼ E i n k ■ ^д У     к = 1 |

1 +

У ^- У к _^{x -} x k

- 1

— x - xk

2.    Визуализация точек фазовой сингулярности

Одним из современных и быстро развивающихся разделов оптики является сингулярная оптика, объектом исследования которой являются волновые фронты с фазовыми сингулярностями. В качестве примера фазовой сингулярности можно назвать оптические «вихри».

Оптический «вихрь» представляет собой деф-фект фазы волнового фронта, где волновой фронт обретает винтовую (спиралевидную) форму.

Первыми работами в области спиралеобразных волновых фронтов и способов их формирования могут считаться работы [18, 19]. В работах [20, 21] тео-

K

=Е к = 1

x - x k

. ^{к ( x -} x k ^{) 2} + ⁽ У ^- У к ^{) 2}

Из (35) и (36) видно, что в окрестностях точек фазовой сингулярности частные производные стремятся к бесконечности:

д ф lim — = » .

(x,у )^( xk, Ук) дx дф lim — = » .

⁽ x , у ) ^⁽ x k , У к ) д у

Из этого следует, что в центрах «вихрей» выражение (30) принимает минимальные значения.

Для эксперимента была смоделирована фазовая функция с пятью спиралями. Изображения (128х128 отсчетов) отдельных «вихрей» (вещественная часть) показаны на рис. 3. При произведении этих «вихрей» было получено изображение на рис. 4 (показана фаза). После применения КПР было получено изображение с интенсивностью, показанной на рис. 5. Из рис. 5 видно, что точки с минимальной интенсивностью соответствует точкам фазовой сингулярности.

а)                  б)                   в)

г)                    д)

Рис. 3. Отдельные изображения функций со спиралевидной фазой (вещественная часть): 2-го порядка с центром в точке (32, 64) (а), 1-го порядка с центром в точке (64, 32) (б), 3-го порядка с центром в точке (96, 96) (в), 4-го порядка с центром в точке (64, 64) (г), 5-го порядка с центром в точке (96, 48) (д)

Рис. 4. Произведение изображений функций со спиральной фазой (фаза)

Рис. 5. Модуль КПР-образа при γ = 1 отсчет: черный цвет – минимальная интенсивность, белый цвет – максимальная интенсивность

Из формул (35) и (36) легко заметить, что частные производные фазы светового поля не только стремятся к бесконечности в окрестностях точек фазовой сингулярности, но и пропорциональны порядку «вихрей». Так, например, в окрестности точки фазовой сингулярности второго порядка частные производные стремятся к бесконечности в два раза быстрее, чем в окрестности точки фазовой сингулярности первого порядка. Именно этим можно объяснить различия в размерах пиков, соответ-свующих точкам фазовой сингулярности разных порядков на рис. 5.

На рис. 6 приведена зависимость энергии в окрестностях точек фазовой сингулярности от их порядков. По горизонтальной оси отложен порядок «вихрей», по вертикальной – энергия, рассчитанная, как суммарная интенсивность в некоторой окрестности пика (размером в несколько отсчетов), на КПР-образе.

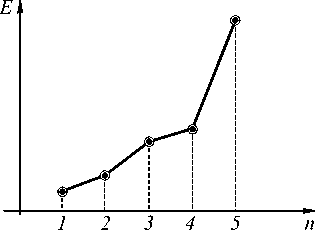
Рис. 6. Зависимость энергии в окрестностях точек фазовой сингулярности от их порядков

Из рис. 6 видно, что действительно энергия функции, полученной после выполнения КПР, в окрестностях точек фазовой сингулярности пропорциональна квадрату от порядков фазовой сингулярности.

Заключение

В данной работе получены следующие результаты:

• •    Численно показана возможность использования КПР для оконтуривания фазы и для обнаружения точек фазовой сингулярности световых полей.

• •    Показано, что энергия функции, полученной после выполнения КПР от светового поля с «вихрями», в окрестностях точек фазовой сингулярности пропорциональна квадрату величины порядков фазовой сингулярности.

Работа выполнена при поддержке гранта Президента РФ № НШ-1007.2003.01, и также российско-американской программы «Фундаментальные исследования и высшее образование» («BRHE») (грант CRDF REC-SA-014-02).