On a Novel Grid Computing-Based Distributed Brute-force Attack Scheme (GCDBF) By Exploiting Botnets

Published Online June 2017 in MECS

Brute-force attacks have been recognized as one the most basic and promising ways for breaking ciphers for a long period of time. In order to neutralize this kind of attack, cryptosystems designers began to further complicate their systems which results in more complexity for breaking them. On the other hand, computing  power has  also  increased. These two approaches create a  close competition between cryptosystems designers and cryptobreakers. Since then, cryptosystems designers found a way to overcome this issue which was: increasing the key space. For a key with length of n binary bits, we have the probability space (or „п key space) of 2й . In average an effort of О (—J order is required to find the actual key. Therefore, a key with long-enough length (i.e., 128bits) requires a very long time to break and it is also computationally expensive to perform. This amount of computational effort and time makes centralized brute-force attacks infeasible in terms of computation time and equipment cost.

Therefore, nowadays brute-force attacks are not as effective as they were at the beginning. In this paper, we devise a novel scheme (GCDBF) which itself basically consists of a combination of three main concepts:

• 1.    Brute-force attacks

• 2.    Botnets

• 3.    Grid Computing

Each of which will be briefly described respectively.

• A.    Brute-force Attack

Brute-force attacks are designed to find keys (such as passwords) with guessing or trying every possible key. For example, cryptobreakers assume that users choose their passwords from a small subset of the full password space, e. g., short passwords, dictionary words, proper names, and lowercase strings [1, 2]. In this case, the attackers attempt to login to user accounts by trying almost all of the possible passwords until the actual one is found. If the cryptobreakers exploit a predetermined list of common or usual passwords, they will be able to perform a dictionary attack, otherwise they space of passwords will be searched by using brute-force attack. Brute-force attacks divide into simple or distributed attacks. In simple attacks or centralized attacks, the cryptobreaker uses only one host that searches for the actual password. In distributed attacks, many cryptobreakers send relatively small numbers of requests at once [2]. It is noteworthy that GCDBF distribution is different than [2] or other similar works, since it conducts brute-force by implementing it by the means of grid computing concepts and botnets’ components.

Brute-force attacks require significant amount of time and processing power when the key space is long. A computer program is usually used to conduct a bruteforce attack. The effort of brute-force should start with one digit password number and cover all possibilities in a worst case [3, 4].

• B.    Botnets

A botnet is a network of thousands of computers (known as bots, zombies or infected nodes) that are infected by a particular malware and are controlled by a bot master (or bot herder) [5]. Bot herder (person who creates the bot and is able to control it remotely) send commands to a server, which relays those commands to infected nodes. Upon executing the commands, nodes will inform the bot herder about the results. In this paper, we do not determine any specific means to create a botnet, since it is not our contribution nor our concentration. Botnets usually include these components [6]:

• •    Command and control: it is the infrastructure including servers and other technical infrastructure needed to control the malware and subsequently, to control the botnet.

• •    Zombie node (also known as infected node): a zombie node is a computing device with internet connection which is being controlled by a hacker after infection by the means of a malware.

Generally, following steps are in common for constructing a botnet:

• 1.    Bot herder builds/purchases a malware and/or an exploit toolkit (in the applications or operating system).

• 2.    Bot herder uses the acquired tool (bot) to infect the computing devices.

• 3.    Bot on infected devices logs into predetermined command and control (C&C) server.

• 4.    Bot herder uses these devices to perform desired set of operations.

• C.    Grid Computing

Grid computing comes from a new computing architecture [7] and is changing into a common technology for large-scale resource sharing and distributed system integration [8, 9].

Grid computing can also be used for computingintensive tasks. As some of the most anticipated public projects, SETI@Home [10] and Distributed [11] are using grid computing to reach their goals. A computational grid is the cooperation of distributed computer systems where user jobs can be executed either on local or on remote computer systems. On one hand grid computing provides the user with access to locally unavailable resource types, especially for individual cryptobreakers and on the other hand there is the expectation that a larger number of resources are available. It is expected that this will result in a reduction of the average job response-time [12].

• D.    Overview of GCDBF

In summary, our main contribution is to integrate the concept of grid computing with the concept of botnets to perform brute-force attacks with a practical and low-cost equipment and in low-computation time in a distributed manner. GCDBF works as follows: First, it is assumed that there exists a botnet. This botnet will be used for processing a portion of an overall process with the use of grid computing concept, in contrast to other works that exploit botnets for DoS and DDoS [5, 13]. In order to use this botnet, a main control and command center divides the whole process of breaking a key into several (thousands) of sub-processes and assign each sub-process to an infected node. Each infected node uses a portion of its idle computing component (i.e., processor) to perform the assigned process. This way we can gain a granularity which was not available in the traditional brute-force schemes. Upon finding the actual key, the infected node in which the actual key is found informs the control center about its success and sends the actual key along with informing message. Therefore, instead of having a limited set of computers with limited granularity which was the result of not being able to scale in centralized brute-force schemes, we have a large set of independent-distributed computing devices with large granularity that exploit a portion of their idle processing powers to perform the overall process. The rest of this paper is organized as follows: first, we study about some related works; Then, GCBDF is described in details and in the evaluation section implementation of proposed schemes is examined in different scenarios.

• II.    Related Works

There are several works in which brute-force attacks are examined, but to the scope of authors’ knowledge there has been no organized scheme for performing bruteforce attacks in a distributed manner by exploiting botnets. However, there are several works in the context of brute-force attacks, grid computing and botnets which have been used in this paper.

In the context of brute-force attacks, authors in chapter 5 of [14] present some information about the definition and applications of brute-force attacks. In [2] researchers presented a review on brute-force attacks along with network behavior of these attacks and a scheme to encounter them. Authors in [4] propose a new scheme for defending against distributed brute-force attacks and presents some information about distributed brute-force attacks.

In the context of botnets, researchers in [6] presented a survey on life cycle and categories of botnets and countermeasures against them. Authors in [5] discuss the application of botnets in performing DDoS attacks. Researchers in [13], discussed mobile botnets as one of the most recent threats in connected environments such as organizations or home networks. Authors in [15-17] propose taxonomies on mobile botnets. In [18, 19]

researchers propose new schemes to exploit cloud environments for botnets.

In the context of grid computing, authors in [20] discussed some information about grid computing including its history and existing works. Researchers in [9] devise a workflow management scheme for grid-based environments and in [12] authors established grid computing applications for parallel job scheduling.

• III.    Proposed Scheme (GCDBF)

In GCDBF, we aim for performing a brute-force attack in a distributed manner (specifically, grid computing) through a botnet. GCDBF can be divided into five main phases:

• 1.    Botnet Construction: Creating a botnet by using a malware.

• 2.    Main-Process Division: Dividing the whole operation (breaking the key with brute-force) to thousands of equal sub-operations in the control center.

• 3.    Chunk Assignment: Assigning each sub-operation to an infected node in a random manner.

• 4.    CPU Scavenging: Forcing the infected node to perform the sub-operation with its idle computing power.

• 5.    Code-Breakage Alarm: Upon finding a collision, the bot should inform C&C center.

• 3.1.    Architecture of GCDBF

• 3.2.    Explaining GCDBF Phases

Architecture of GCDBF and details of each phase will be described respectively.

As it will be described in the next sub-section, since GCDBF is an integration of botnets into grid computing, it has components from both contexts. The overall architecture of GCDBF is illustrated in Fig. 1.

As illustrated in Fig. 1, the BotHerder (or BotMaster) is the cryptobreaker who is in control of the bots. This BotHerder should set up a control and command center with required server(s) and communication infrastructure.

Number of required servers is determined by parameters such as botnet size (number of infected nodes), main-process (key space) and processing power of each server. If more than one server is required, there should exist a Main Controller which is responsible for dividing the main task as well as dispersing it in a balanced manner (from the perspective of processing load) to each of the servers and from there, assigning it to corresponding bots. Otherwise, the server itself is responsible for dividing the main task and assigning it to the bots.

From there, servers connect to grid of infected nodes through Internet and bots start to perform the required sub-process. Upon success, bots will inform their corresponding server and therefore, BotHerder will be aware of actual key.

Phase 1- Botnet Construction: As the first step, a botnet should be created. There exist many schemes to create a botnet (see section II) but in this work we use client-server approach to create an IRC botnet. In IRC botnets, infected nodes access a predetermined location (Internet relay chat networks or domains) and wait for command from a predesigned server [6].

In our scheme, these bots will not be used to perform a DoS attack, but to perform a portion of operations of a brute-force attack. It is noteworthy that the size of required botnet to feasibly perform the brute-force attack is proportional to the probability space of the key which is desired to be broken.

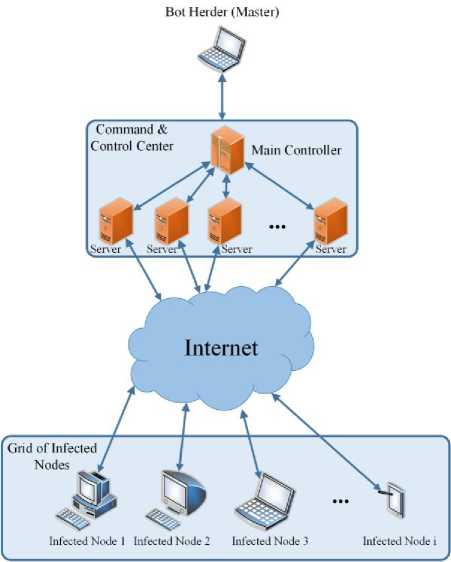
Fig.1. Architecture of GCDBF

On the other hand, we have the concept of distributed computing and specifically grid computing that aggregates multiple computing devices to perform a single but large task. As mentioned in [12], both distributed and grid computing are counted as a special forms of parallel computing which uses several complete computers (devices with processors, storage, power supply and network interface) which is connected to a network (such a s internet) to perform a single large task by dividing it into several smaller tasks running on several computers instead of a single large task running on a conventional or super computer.

By comparing the concept of botnets and grid computing, in this work these two concepts are merged together and mapped to each other:  using a grid/distributed set of computers (bots) which are connected through a network (internet) to perform a large task (a brute-force attack).

The logic behind choosing botnet/grid computing to perform a brute-force attack is to reduce the computational time and computational cost (in terms of high-end equipment and infrastructure) which is required to break keys with large probability spaces. Achieving this goal will make brute-force attack on long keys feasible for individual cryptobreakers in terms of operation-time and cost while it does not need high-end infrastructure and can be performed via commonly used hardware.

Phase two - Main-Process Division: One of the basic features of grid computing is dividing the large task into several smaller chunks (units of operation). Usage of this feature in GCDBF is that the task of performing the brute attack to break a specific key must be divided into smaller chunks. Explaining further, the large task is to examine every probable key in the key space in order to find the correct key. Dividing this task means dividing the size of the key space with number of infected nodes with the condition that size of the key space should be divisible by number of infected nodes. In other words, the number of chosen infected nodes should be the closest number to number of infected nodes that divides the size of key space. Meaning that greatest common divisor (gcd) of number of infected devices and size of the key space should be calculated in the Main Controller-or the server-(grid computing context) which placed in the command and control center (botnet context). The algorithm for this phase can be described as follows:

• 1.    Calculate the size of key space (KSS) (number of all of the probable keys).

• 2.    Calculate the number of infected nodes (inodes).

• 3.    Compute the gcd^KSS, inodes') = i .

• 4.    Divide the KSS by ^i:^T=j

To compute the chunk size (number of keys to be examined by each infected node.)

Phase 4 - CPU Scavenging: CPU Scavenging or Cycle Scavenging is a technique which is introduced in grid computing context and uses idle processors instruction cycles to perform the assign chunks of processing task. CPU scavenging has multi models of implementation, one of which is to create an opportunistic environment that harvest idle computer for performing computationally intensive tasks, known as enterprise desktop grid (EDG)[8, 9, 20]. These methods often include a job querying policy, scheduling mechanism and etc. that will help reducing the complexity of implementation.

Color figures will be appearing only in online publication. All figures will be black and white graphs in print publication.

• IV. Proposed Scheme (GCDBF)

In this section, GCDBF scheme is being examined in different scenarios to prove its feasibility and performance (with respect to relevant performance metrics in each scenario) against centralized brute-force attacks. A common assumption in all scenarios is that it is assumed we already have the required botnet. Having this assumption does not simplify the proposed work, since the contribution of this paper is to exploit botnets for performing a brute-force attack (instead of a DDoS attack) and therefore explaining details on constructing a botnet is out of this work’s scope. In the first scenario, the performance of centralized brute-force is compared to that of GCDBF to show how the botnet size (computation power) affects performance in terms of computation time. Another important parameter is the key length which its effect on performance of centralized brute-force and GCBDF is examined in 2nd scenario. 3rd scenario is designed to show how different key structures affect the performance of GCDBF scheme in comparison to centralized brute-force with respect to computation time.

Prior to describing the scenarios, there are some parameters which must be defined.

Average Assigned Workload (AAW): AAW in distributed processing applications is the average portion of total workload assigned to be solved by a specific processor. Assigned workloads consider average processor capability, average processor utilization and an average online and available time. Currently, AAW is 2 to the 33 power of CPU capability for ½ hour of CPU availability per session at less than 10% of CPU utilization for Pentium processors which is equal to almost 17 billion entry tries per hour [11].

Feasibility of an Attack: we defined the feasibility of an attack with respect to these conditions:

• ■    Computation time: the time required to break a specific key. If the process of breaking a key exceeds a certain deadline, it would be counted as infeasible. The mentioned deadline should be determined with respect to application and context.

• ■    Computation cost: the cost of computation equipment and communication infrastructure: In this paper it is assumed that it is impossible for hackers to completely acquire super computers and are not able to use such processing capabilities.

• ■    Key Space: total number of all of the possible comparisons needed to decrypt an encrypted stream of characters.

• ■    Law of Averages: considering that it is required to find a specific key by trying to examine every possible key, if the key space be n, we will have:

• ■    Best Case: first examined key is the actual key. So

the order of the effort is of      .

• ■    Worst Case: last examined key is the actual key. So the order of the effort is of      .

• ■    Average Case: the possibility of occurring best case or worst case is significantly low (the probability of each one is ). In fact actual key can be found anywhere in the key space, therefore in average case          of key space through all of

the possibilities should be tried to find the actual key and the order of the effort is as order of     .

• ■    Total Workload: all of the possible keys that must .             .           .                  .    . ksv space

• 4.1.    First Scenario

be tried to decipher a given code which is         .

Some of the calculations of this work such as dividing the main-process task into chunks are done with the help of Brute-Force Calculator [21, 22].

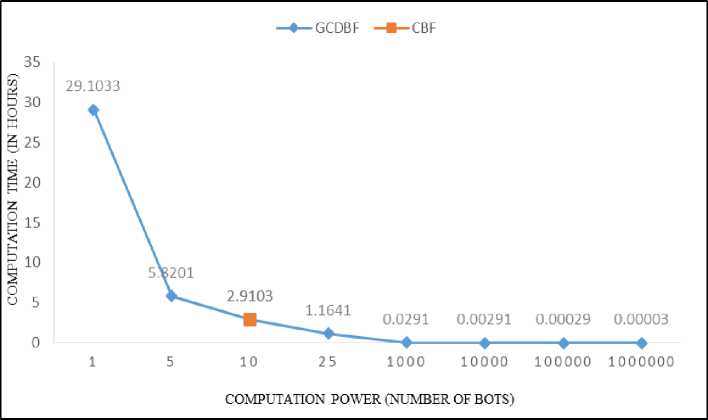
Fig . 2. First Scenario

In this scenario, parameters are assumed as follows:

• ■    Performance Metric: computation time (time that is needed to process the total workload) in hours.

• ■    AAW: is 2" in - hour which is 2 2^LL = 2^L' in an hour (assumed computation power of each computer (infected node) in the botnet in the proposed scheme).

• ■    Total GCDBF’s Computation Power: since this scenario aims to show the effect of botnet size on performance, botnet size is gradually increased and will be selected from the set of

,,                                 .

• ■    Centralized brute-force’s (CBF) computation power: we assume that cryptobreaker utilizes 100% of his/her processor’s power, the corresponding computation power will be

floating point processes (in fact he/she has     more computation power in comparison to a single infected node).

• ■    Key: in this scenario, key randomly consists of 12 characters including integer numbers (0-9).

• ■    Key space: 2   2."" (1 quadrillion combinations)

• ■    Total workload: 2   2."" floating point processes.

• 4.2.    Second Scenario

As we can see in Fig. 2, the total workload is constant for GCDBF and Centralized Brute-force (CBF). It is observed that at first, GCDBF (black-colored line) has lower performance in comparison to CBF (white dot) in terms of computation time. Namely, with 1 bot the performance of the GCDBF is about 10% of that of CBF. With 5 bots, although we observe performance improvement in GCDBF but still its computation time is about 50% of that of CBF. Upon increasing the size of botnet (meaning adding bots to botnet) the aggregate computation power increases and therefore, at the point of 10 bots, performance of GCDBF and CBF converges in 2.9 hours of computation time for a total workload of floating point processes. From this point on, GCDBF outperforms CBF in terms of computation time. For example, with 25 bots, its performance is more than twice of that of CBF. With 1000 bots, the key will be broken in 0.02 hours (about 1.2 minutes). So as it is obvious, the task which requires 2.9 hours of computation time at 100% utilization, can be done within 7.2 seconds at 10% idle processor time in 10000 computers. This outperformance in GCDBF comes from the fact that centralized systems are unable to scale. This is why we have a line for GCDBF and a point for CBF (since its computation power cannot change).

Another important point about size of botnets is that, they vary from thousands to millions [5, 6], so it is not impractical to assume that our botnet has 100000 bots or more.

In this scenario, parameters are assumed to be as follows:

• ■    Performance metric: computation time (time that is needed to process the total workload) in hours.

• ■    AAW: is 2^LL in - hour which is 1 2^LL = 2^L' in an hour (assumed computation power of each computer (infected node) in the botnet in the proposed scheme).

• ■    Total GCDBF’s Computation Power: in this scenario we consider the size of the botnet equal to 10000 so total computation power of GCDBF would be           floating point processes.

• ■    CBF’s computation power: we assume that cryptobreaker utilizes 100% of his/her processor’s power, the corresponding computation power will

be                               floating point processes (in fact he/she has 10x more computation power in comparison to a single infected node).

• ■    Key: since the effect of key length on performance metric is going to be examined in this scenario, the key length would be gradually increased and will be chosen from the set of {10,11,12,13,14,15,16}. Key consists of integer numbers from 0-9.

• ■    Key space: would be different in accordance to key length.

• ■    Total workload: would be different in accordance to key length.

• 4.3. Third Scenario

As we can see in Fig. 3, GCDBF deploys 10000 bots and therefore it outperforms CBF from the beginning. For a key with length of 10 which requires        floating point processes to break, GCDBF will find the actual key in 0.036 seconds while CBF needs about 72 seconds. For a key with length of 11 which requires          floating point process to break, GCDBF will do the work in 0.36 seconds while CBF needs about 17 minutes. As the key length increases, the difference in performance between GCDBF and CBF increases too. For example, for a key with the length of 16 with the total workload of         ,

GCDBF needs 29.1 hours (about 1.2 days) of process with 10000 bots at 10% utilization (which is a relatively small botnet with relatively low utilization) while CBF requires 29103.8 hours (about 1212 days or about 3.3 years) of process at 100% utilization.

Data set for this scenario is attached below the Fig. 3.

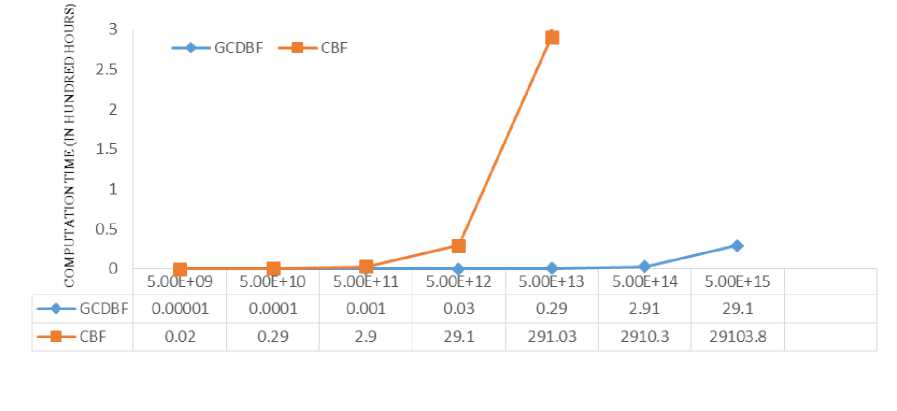
Fig.3. Second Scenario

In this scenario, parameters are assumed as follows:

• ■    Performance metric: computation time (time that is needed to process the total workload) in hours.

• ■    AAW: is 2^1L in - hour which is 1 2^LL = 2^L~ in

an hour (assumed computation power of each computer (infected node) in the botnet in the proposed scheme).

• ■    Total GCDBF ’ s Computation Power: in this scenario we consider the size of the botnet equal to 10000 so total computation power of GCDBF would be           floating point processes.

• ■    CBF’s computation power: we assume that cryptobreaker utilizes 100% of his/her processor’s power, the corresponding computation power will be                               floating point

processes (in fact he/she has 10x more computation power in comparison to a single infected node).

• ■ Key: in this scenario, the key length is considered to be 10 but the key structure varies in order to show how it affects the performance metric. Key structure would be as follows:

o Set 1: Randomly selected integer numbers from 0 to 9.

o Set 2:  randomly selected alphanumeric

(lowercase or uppercase English Alphabet letters)

o Set 3: randomly selected alphanumeric (both lowercase and uppercase English Alphabet letters)

• ■    Key space: would be different in accordance to key length.

• ■    Total workload: would be different in accordance to key length.

As we can see in Fig. 4, for the first set of key characters, we have the total workload of floating point processes required to break a key of length 10, GCDBF will find the actual key in about 0.036 seconds, while CBF finds the key in 72 seconds. For the second character set, which results in total key length of 36 (26 for upper/lower case letters plus 10 for numbers from 0 to 9) that requires total workload of           .

Considering this set, GCDBF needs          hours to break the key, while CBF requires           hours to find the actual key. As it is obvious in the Fig. 4, again we can see the outperformance of GCDBF against CBF, which will result in lower computation time by hundreds of time, while it doesn’t need acquiring expensive hardware such as supercomputers.

In this section, GCDBF is compared against CBF to show how it outperform centralized brute-force schemes. In addition to decreased computation time which make GCDBF a feasible solution for many applications in terms of required time to break the key, this scheme is practical since in our evaluation we used statistics of Intel Pentium processors which are commonly used since their introduction about 14 years ago. This is an important point since many of desktop computers has moved to the next generations of Intel CPUs which have tens of times more processing power in comparison to Pentium CPUs. As a result it can be stated that practical implementations of GCDBF over average desktop computers will have even less better performance in terms of computation time.

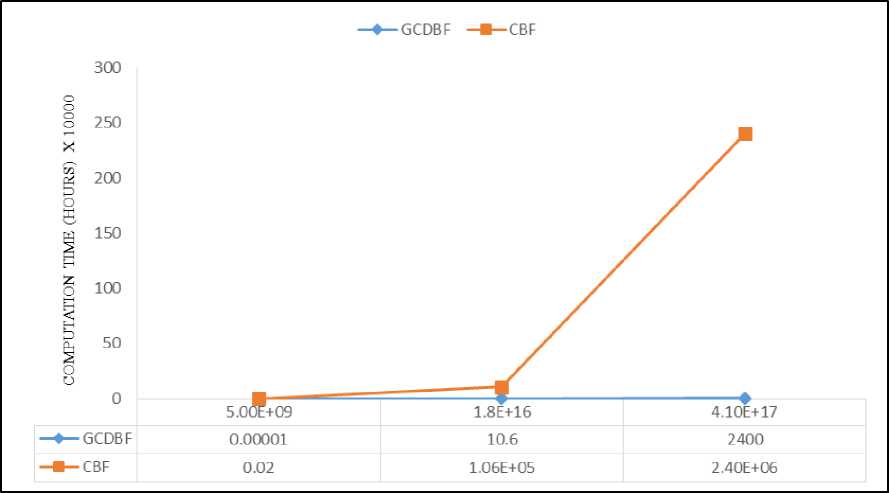
Fig.4. Third Scenario

V. Conclusion

In this paper, authors devise a new brute-force attack scheme GCDBF, in which they integrate concepts of grid computing paradigm with components of botnets in order to reduce the computation time required for breaking a key with the brute-force scheme. Along with the reduction of computation time, this scheme does not need any expensive equipment such as supercomputers and because of that, it makes the brute-force attack on long keys feasible for individual cryptobreakers who has access to average-sized botnets. Several evaluation results show that GCDBF significantly outperforms centralized and conventional brute-force attack schemes in terms of computation time needed to break a key. Future works on GCDBF includes exploiting mobile botnets, devising a scheme based on GCDBF for performing mobile bruteforce attacks and implementing GCDBF in a real world environment.