On Calculation of Fractal Dimension of Color Images

Published Online March 2017 in MECS

The fractal geometry is a concept which was firstly invented by Mandelbrot for express self-similar sets of fractals images like mountain and cloud which are unfeasible to illustrate by means of classical geometry [1]. The concept Fractal geometry is broadly used in many application of image processing in terms of the precise evaluation of dimension of complex and irritated objects. These concepts are primarily evolved to decrease the differences of surface roughness among the artificial designs and natural scenes. Since artificial designs typically have a plain and simple texture surface and measure geometry shape, from this point of view, this concept are easily used in various recognition of pattern applications such as categorization and segmentation and many more. The major parts of fractal geometry are called self-similarity. The theory of self-similarity should be defined as the object is precisely or something like related to a part of itself; alternatively we can say that if a surrounded set A is supposed to be self-similar, if A is the unification of a number (Nr) of non-overlapping scaled copies of itself, where r is the reduction factor reported in [1]. Fractal geometry also gives a mathematical special model of various difficult objects initiate in nature [1-3], that includes coastline, mountains, and clouds and also it has been useful in different texture analysis such as segmentation [4-6], shape measurement and classification [7], image and graphic analysis in different fields [8, 9]. In this regard, different researchers are contributed their work, such as Gangepain and Roques-carmes presented reticular cell counting method [10,11] and later on Keller et al. proposed probability box counting [10,12]. Both Gangepain and Keller gives the satisfactory result, but after reaching a particular level of image intensity surface then the slope of the arc tends to zero; therefore both the methods does not estimate the accurate FD. In order to avoid such situation, Sarkar et. al. presented a novel technique called differential box-counting (DBC) technique [4, 10, 13], this DBC method treated as the efficient one found in many articles like[14,15]. However in the case of DBC method there are three major problems reported by Jain et. al. [16]. Which are box height selection, calculation of the box number and partition of the image intensity surface? In order to avoid these situations, the same author presented another method called an improved box-counting method [16] in order to avoid the three above mention drawbacks of DBC method. Again some demerits found in DBC method reported by Chen.et.al [17] that is over-counting and under-counting. To avoid such situation the same author [17] presented another method called improve DBC. The box-counting algorithms are often used for estimation of surface roughness due to its easiness reported in [3].

A reminder of this article is as follows; Section 2 presented the essential ideas about fractal dimension and FD estimation of color images. Section 3 discusses proposed methodology. Section 4 describes experimental result and discussion and concluding remark are presented in section 5.

• II.    Basic Fractal Dimension

A set can be defined as a fractal, for which the Hausdorff Besikovich dimension is firmly bigger than the topological dimension. The estimation of fractal dimension is a necessary feature of fractal for the cause that it has got information concerning their geometric structure. The fractal dimension of the entire images generally distribution of intensity values, more deliberately, estimating the roughness of an entire image. The basic theory to estimate roughness of a whole image depends on the theory of self-similarity. From the property of self-similarity we can say that the fractal objects are normally an irregular or inexact geometric shape, if we assume the fractal object is the combination of N distinct of non-overlapping copies of itself, each of which is similar to the original and the ratio factor are scaled down or up by r, then the fractal dimension D is given by equation (1).

log( N ) log(1/ r )

• A.    Improved Differential Box-Counting

Liu.et.al [18] suggested improved DBC method for eliminating the demerits found on original DBC method that is over counting and under counting. In this regard to implement their method, they taking into consideration by which maximum and minimum intensity value falls in grids of the block. First of all, they taking an image of size M×M in 3D space, where the coordinate of (x, y) and coordinate (z) represents the 2D position and gray level. Then they scaled down the total no of pixels into box size of l x l where l is lies between 1 to M/2 and estimate r = l /M. On each box of the block, there is a pillar of boxes of total size is s x s x s’, and s’ represents the height of each box and it can be calculated as G/s’ =M/s, where G represents the total gray-levels. The minimum and maximum gray levels are represented as I_min and I_max respectively in the (i, j)th block. Then the total number of boxes needed to cover the block in the z direction is nr old and after shifting the δ positions from nr old , nr new is calculated. Maximum of nr old and nr new is taken as nr. nr=max(nr old , nr new ). nr old or nr new is calculated as follow:

nr(i,j) = ceil ‘

I max I min + ¹

1 s

I if—¹ max * I min

Otherwise

And Nr will be calculated as

Nr =E ⁿr ⁽ i , j )               (3)

The fractal dimension (IDBC) is calculated with regression plot between log (N) vs log(1/r).

There are many algorithms were proposed in terms of gray scale and color approach. Maximum of research are done using grayscale image like reticular cell counting method [11], kellers approach [12], Differential box counting method [13], Improved differential boxcounting method [17] and only two research papers have been evolved so far in case of color images like color version of probability method [19] is the modified version of Keller approach and box merging method [20] is the extended version of box counting mechanism. However In this article we have considering improved differential box-counting method which has already been developed for estimating fractal dimension of gray scale image and added our proposed methodology to efficiently estimate the fractal dimension of color image and compared with color version of box merging method with different experimental analysis in terms of different class of color texture images and known fractal dimension images and shows the time complexity of both algorithm.

• B.    Fractal Dimension Estimation of Color Images

Nowadays the world of images became colored. Digital color images are related to grayscale images and the pixels are arranged in a grid of boxes. However, in the case of color images, each individual pixel has three sampled value mainly red, green and blue. Therefore estimating fractal dimension of color images is a very challenging issue. Therefore in this regard, extremely limited approaches that connect to calculate the roughness of color images and the principle is only constrain to trivial color investigation and convert a gray scale problem into a false color one [20].

• III.    Proposed Methodology

The color estimation proposed by Ivanovici and Richard [19] called probabilistic algorithm is given by Voss and another method developed by Nikolaidis et al. [20] called box merging method based on the concept of box counting mechanism and Zhao and Wang [21] presented another box counting based on the concept of maximum color distance to estimate roughness of color images based on the 5-D vector. In order to validate their both methods, Ivanovici and Richard [19] generate color fractal images based on Hurst parameter by using the technique of the midpoint displacement algorithm and Nikolaidis et al. [20] used known fractal dimension image and checked for validation. However, we are proposing improved differential box-counting method based on the same 5-D vector to estimate roughness of color images using the RGB components of the color image, which roughness is lies between 2 to 5. Therefore in order to estimate roughness of color image, we first estimate roughness of each individual RGB component and subtracted its corresponding smoothness. After subtraction of smoothness, we will take its fractional part and add its corresponding RGB components and finally the addition of smoothness to get accurate roughness.

DR = DIDBC ( R ) - ²

DG = DIDBC ( G ) - ²

DB = DIDBC ( B ) - ²

DColor = ² + DR + DG + DB

• A. Algorithm Summery

The detailed algorithm can be summarized as follows:

• •    Picking the different grid box sizes of 2 up to M/2 to wrap the whole image.

• •    Take into account the number of the total boxes require to cover the image entirely.

• •    Using the slope of least-squares linear fit of log (Nr) vs log (1/r) to achieve the FD of each red, green and blue channels.

• •    After calculating FD of each individual channel, we subtracted its corresponding smoothness and take its fractional part and add its corresponding RGB components and finally addition of smoothness to get accurate roughness.

• IV.    Experimental Analysis

  In this study, our proposed method is implemented on matlab14 in windows 8 64 bit operating system, Intel (R) i7 – 4770 CPU @ 3.40 GHz. Our proposed method and box merging method have been chosen for our four sets of images for this experimental analysis, shown in Figs. 1 to 4, and one set of 16 color textured images downloaded from Brodatz database [18], shown in “Fig. 1,”. One set of 8 own created textile fabric of exactly similar texture with varied color were collected for this ground truth experiment shown in “Fig. 2,”. The images were taken in color viewing cabinet with D65 illuminant, viewed at 45-degree angle with white balance in manual mode. As the last test, we are taking four set of smooth known fractal dimension image which fractal dimension was measured as 2, shown in Table 3.

Our details procedure is listed in Table below

	Start Read image                                      % input the image
Step (1)	For i=1:3; Img(i)=(:,:,i); [p,q]=size of (img(i));                                % read the sizes of the image Select exact grid box size g(b); B=1;                                              % using B as a variable of different grid box sizes
Step (2)	While (g(b) r=g(b)/p;                                              % define r
Step (3)	For i Count nr-old;                                              % use (2) Move the box block in (x,y) plane within t pixels;     % under the set rule Count nr-new;                                          % use (2) nr=max(nr-old,nr-new); End for Nr=sum(nr);                                        % calculate the total number of boxes B=b+1;                                            % for using dissimilar grid box sizes End while Call fit (logNr,log(1/r));                                 % execute least-squares linear fit Obtain FD of img(i);                     % FD equal to the slope of the fitted line of each channel
Step (4)	Dcolor=2+(FD of img(i)-2);                          %Color FD estimation using(4) End for End

• A.    Result and Discussion

Using the improved differential box-counting method to estimate the fractal dimension of color images in terms of its smoothness, for the same we are estimating the FD of color images using the individual red, green and components of the input color image based on the same 5-D vector, which roughness is lies between 2 to 5. Therefore in order to estimate roughness of color image, we first estimate roughness of each individual RGB component and subtracted its corresponding smoothness. After subtraction of smoothness, we will take its fractional part and add its corresponding RGB components and finally the addition of smoothness to get accurate roughness of color images. For our experimental work, we took three different class of texture images, first of all for our first experimental analysis we have to consider different texture taken from Brodatz’s image database [18] given in “Fig. 1,” and it shows that D93 image has got more color roughness as per both box merging and our proposed method, also from Table. 1, it is clear that those texture images having more color roughness as estimated in box merging method are also having the higher roughness in our proposed method. However, it seems from Table. 1 that method proposed by us is able to compute higher color roughness based on the RGB components of the color texture. For our second experimental analysis, we are considering our own created eight textile fabric of exactly similar texture with varied color were collected for this ground truth experiment shown in “Fig. 2,”. The images were taken in color viewing cabinet with D65 illuminant, viewed at 45-degree angle with white balance in manual mode and the camera specification are listed below. It is clear from the Table 2, that image I2 is having least fractal Dimension and I3 is having highest Fractal dimension among the eight color texture images, this can be easily established by the fact that under natural human perception I2 seems to be having more smoothness and I3 maximum roughness, this has also been validated using box merging method. In last experimental analysis is used for validation purpose, in this case, we are considering four smooth images shown in “Fig. 3,”. All the articles on fractal dimension mention that fractal dimension of the smooth image as accepted as 2.0, also in our case Table 3 indicates that all four images having fractal dimension as 2, hence it is crystal clear that our method is more robust to estimate the fractal dimension of color images.

• B.    Experiment on Real Natural Texture Images

  In this section, we are using a set of 16 real texture images [18] from the brodatz database for our experimental analysis, which is represented in “Fig. 1,” Their corresponding FD are listed in Table 1. The FD generated from proposed method are in the range from 2.6503 to 4.1718, similarly, the other measure like box merging method are range from 2.4829 to 2.5868 and 3.5155 to 2.5821 respectively, and the detail graph is presented in “Fig. 2,” from this result it is crystal clear that our proposed method efficiently capture the exact roughness of color images as compared to box merging method.

Fig.1. Sixteen real texture images.

Table 1. Fractal Dimension of Sixteen Real Texture Images

Image Name	Proposed	Box Merging
D8	3.1268	2.9327
D11	3.9343	3.3754
D23	3.5673	3.5070
D38	3.7363	2.8334
D55	4.0583	3.4889
D62	3.1462	3.3308
D56	3.5793	2.8243
D69	3.7475	3.0567
D71	3.8522	3.0087
D89	3.2513	2.9213
D90	3.0201	2.6285
D91	2.6503	2.4829
D93	4.1718	3.5155
D98	3.0779	2.8149
D99	3.1934	3.0304
D100	3.8735	3.5007

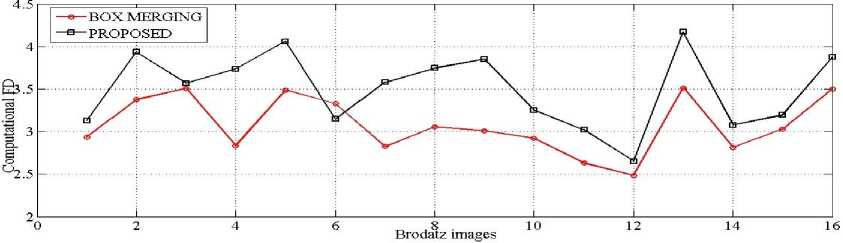
Fig.2. Computational FD of sixteen real texture images.

• C.    Experiment on Own Created Texture Images

In this section, we are using a set of 8 of controlled experimental fabric images with varied color and texture, which are represented in “Fig. 3,” Their corresponding FD are listed on Table 2, from the visually inspection we have seen that image I2 is more smoother than other images, as it is smoother then FD should be less than other images as mention on Table 2, our proposed method provides FD greater than 3 except I2 images but in the case of box merging method, the only I3 image provides FD as greater than 3 and all other images having FD between 2 to 3. From this point, it is crystal clear that our proposed method efficiently captures the exact roughness of color images as compared to box merging method.

The specification of camera and imaging are as follows for our own created texture image shown in figure.2

Camera model:	NIKON D5100
F-stop:	f/5.3
Exposure time:	1/60 sec
ISO speed: 2000
Exposure bias :	+0.7steps
Focal length :	40mm
Max Aparature :	4.8
Aperture mode :	Centre avg.
Tv(Shutter Speed)	1/200Sec.
Av(Aperture Value)	F5.6
Metering Modes Center
Exposure Compensation	+2/3
ISO Speed	2000
Lens Focal Length	55.0 mm
Image size	4928 x 3264
White Balance	Manual
Parameters	(Normal(-))
Sharpness level :	Normal
Contrast :	Normal
Sharpness :	Normal
Color saturation :	Normal
Color tone :	Normal
Color Space :	sRGB

Table 2. Fractal Dimension of Eight own Created Texture Images

Image Name	Proposed	Box Merging
I1	3.4712	2.8379
I2	2.6839	2.4818
I3	3.8591	3.1798
I4	3.4151	2.6646
I5	3.2723	2.8894
I6	3.3925	2.7117
I7	3.5295	2.8153
I8	3.1442	2.6667

Fig.3. Eight own created texture images.

• D.    Experiment on Known Fractal dimension Images

In this section, we are using a set of 4 smooth texture images with varied color, which are represented in “Fig. 4,” .Their corresponding FD are listed on Table 3, from this experimental analysis, we have seen that our proposed method also able to capture smoothness of color images.

Fig.4. Four known fractal dimension smoothed images.

Table 3. Fractal Dimension of Four Known Fractal Dimension Smoothed Images.

Image Name	Proposed	Box merging
a	2	2
b	2	2
c	2	2
d	2	2

• E.    Experiment on Synthetic Images

In this experimental setup, Twelve synthesize images are generated with maximum gray level of 255 of each red, green and blue channel, which are represented in “Fig. 4,”. In this process, each image ware generated from original image by incrementing each intensity point (by formula 2 x(k - 2), where k lies from 1 to 12) in such a way that at the kth image of 12th image, the maximum gray level should not exceed 255 for each channel, therefore alternatively we can say that all the intensity surface are only shifted to up some gray levels from the original one in z direction. Theoretically it was clear that, if we either increasing or decreasing by a constant value, then the FD should stay same as original one because theoretically both have equal degree of roughness. The estimated FD are listed in Table 4 and graph are represented in “Fig. 5,”, from the result, we have seen that our proposed method indicates same roughness for all the images but box merging method does not provides wider range of FD.

Fig.5. Twelve synthetic generated images

Table 4. Computational FD of Twelve Synthetic Images.

Image Name	Proposed	Box merging(BM)
S1	3.8735	3.5007
S2	3.8735	2.8651
S3	3.8735	2.8797
S4	3.8735	2.8571
S5	3.8735	2.8628
S6	3.8735	2.8039
S7	3.8735	2.7948
S8	3.8735	2.7250
S9	3.8735	2.6275
S10	3.8735	2.6228
S11	3.8735	2.6180
S12	3.8735	2.6229

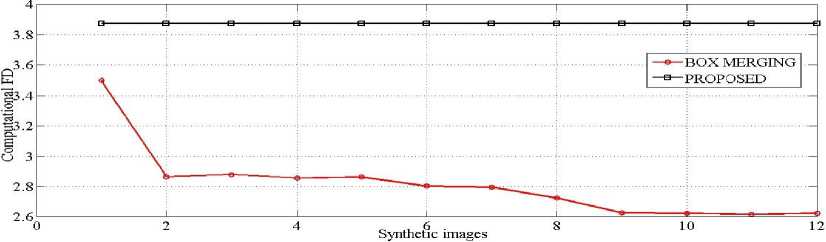
Fig.6. Graph of Twelve synthetic generated images

• V.    Conclusion

In this paper, we presented a color extension of the improved differential box-counting algorithm, which was widely used to compute the fractal dimension of gray scale images. Theoretically, for a color image is a 5-D fractal. As color image consists of more intensity levels than the grayscale image, the fractal dimension method suggested by us indicates an estimation of the much better accuracy of roughness. The fractal dimension of more than 3.0 we measure indicates the fact that our algorithm it is able to capture the complexity of a color image.