On Classical Cryptographic Protocols in Post-Quantum World

The following questions initiated this work:

Q1) If suddenly it turns out that powerful quantum computers start breaking the cryptographic protocols all over the globe, are we able to switch to alternative algorithms to maintain a restricted however efficient (fast enough) service for the protection of sensitive data transmitted over open communication networks?

Q2) Can we do it even in UC-secure way, i.e. keeping provable security guaranties in arbitrary concurrent environment?

Q3) For what kind of protocols and for what kind of corresponding cryptographic primitives can we provide such strong guaranties when we have bound also to efficiency requirements and when we are not?

Our intuition origins in the wide belief that there exists (classical) symmetric key encryption transformation which resists attacks launched even from quantum computers, e.g. the AES algorithm with appropriate key length. This way tasks for securing network communications (secure channels, authenticated channels, shared key refreshing) could be achieved by efficient implementations. In contrast, running public key primitives on classical computers is notoriously very time consuming (e.g. RSA, DSA, ECDSA), let alone those public key ideas which are believed to resist attacks even from quantum computers (e.g. code-based or latticedbased cryptography) ([2], [3], [15]). Our approach is in consonance with a recent presentation in an ETSI workshop on post-quantum cryptography, where a key claim was the following: “A "good" symmetric key based system may prove to be very beneficial in many applications” ([4]). It has been proven that applying Grover's algorithm to break a symmetric key algorithm by brute force (by attempting to guess the secret key) requires time equal to roughly 2 ^n/2 invocations of the underlying cryptographic algorithm, compared with roughly 2 ⁿ in the classical case, meaning that symmetric key lengths are effectively halved: AES-256 would have the same security against an attack using Grover's algorithm that AES-128 has against classical brute-force search. Therefore, we could classify AES as quantum resistant as long as the best-known attack is still some form of exhaustive search of the keyspace. The most important standard applications of symmetric key cryptography are message encryption, message authentication, and key exchange/refresh. The key primitive behind these tasks is the symmetric key encryption.

For refined positioning of our models, we cannot skip some issues on the terminology, in particular regarding the following terms: quantum and post-quantum cryptography, classical security as well as quantum standard-security. The research in post-quantum cryptography aims to propose cryptographic algorithms that are not efficiently breakable by an adversary using quantum computers. In post-quantum approach, we consider classical (non-quantum) protocols and primitives which are run by honest parties on classical computers. Post-quantum cryptography is unrelated to quantum cryptography, where the latter refers to building cryptographic algorithms using quantum phenomena, i.e. where not only the adversary but also the honest parties rely on quantum computation and communication ([9], [10]). In the terminology of M. Zhandry [19], [20] we consider (quantum) standard-security, where the adversary can send only classical inputs to honest algorithms, i.e. honest machines cannot receive quantum superposition of inputs. We will call an algorithm quantum-secure if its security holds against polynomialtime quantum adversary, except when we want to distinguish clearly the computational and the statistical (unconditional) quantum security. Furthermore, we will use attribute classical for computational (non-quantum) case.

In this paper we will treat all three questions posed in the beginning of the chapter and based on previous researches we propose a technique which leads to positive answers.

The structure of the paper is the following. Section 2 presents an outline of the approach. Section 3 contains our main propositions (Proposition 1, Proposition 2) regarding the approach. The case of quantum standard-secure symmetric key primitives and protocols are considered in Section 4, where examples are also presented. Summary concludes the work in Section 5.

The structure of the paper is the following. Section 2 contains related works. In Section 3 we give an outline of our approach. In Section 4 we present our main propositions (Proposition 1, Proposition 2) regarding the approach. Quantum standard-secure symmetric key primitives and protocols are considered in Section 5, where examples are also presented. Section 6 concludes the work.

• II.    Related Works

Our proposed technique we call full factorization. We start from a protocol which is classical UC-secure. Our first step aims to obtain a statistically-secure hybrid protocol one where all cryptographic primitives are substituted by appropriate ideal functionalities. Hence, we apply the Unruh's Quantum Lifting Theorem and Quantum Universal Composition Theorem [16] to arrive at a computationally quantum UC-secure protocol. The ideal functionalities for the considered primitives are the following: for symmetric key encryption, public key encryption and digital signature we refer to the models in [13], [7] and [14], respectively.

With the aim of exploring the set of achievable cryptographic tasks in post-quantum world, the closest work to ours is ([12]), which provides existence theorems. It studies the existence of two-party protocols which are UC-secure in the presence of quantum adversaries. Their main result states that under the assumption of the existence of quantum secure pseudorandom generator (PRG) as well as the existence of special quantum semantic secure dense public-key cryptosystem, there exists nontrivial classical protocol which UC-realizes any well-formed two-party functionality in the ZK-hybrid model, in the presence static quantum adversary. Our approach is more pragmatic: we consider also the problem of efficiently implementable protocols which are fast enough for standard usage and at the same time provably secure in post-quantum world. We are interested in concrete protocols rather than in the existence of them. We assume stronger adversary by allowing also adaptive corruption. Furthermore, we are interested in protocols built from scratch in contrary to the cited result with hybrid protocols, hybrid in a core protocol, the zero knowledge. These two works are common in the technical framework in large, when both rely on the UC-framework by Canetti-Unruh. In particular, we will follow the approach of hybrid protocols according to Unruh’s Universal Composition Theorem ([16]). As for the standard- and quantum-UC-framework we will apply Canetti’s and Unruh’s modeling assumptions, general notions and definitions without formally repeating those below and in this respect, we refer the readers to their works ([6], [16]).

In cases when we are not restricted by efficiency requirements we would like to extend beyond pure symmetric key protocols. A related work on classical protocols is the UCSA (Universally Composable Symbolic Analysis) approach of Canetti-Herzog [7]. UCSA approach aims to simplify the UC-assessment of protocols. For so-called simple protocols, the corresponding hybrid protocol is turned into a Dolev-Yao style symbolic protocol. This class of protocols uses only one type of primitives, which is the public key encryption. Informally, a protocol is simple if there are two roles (initiator, responder) and these roles are programs written in a programming language defined in [7]. In this language, the atomic elements are party identifiers, public encryption and secret decryption keys and random challenges (nonces). The set of commands (operations) are pairing (and separation), generation of random element, encryption, decryption, communication (sending, receiving, output) as well as the "if-then-else" operation. When generating the symbolic version of the protocol, the variables of the program are interpreted as elements from symbolic message algebra, where the rules are counterparts of the operations within the protocol. An equivalent but easier symbolic analysis can be carried out instead of the computational one. The application examples in [7] cover the tasks of mutual authentication and key exchange. Paper [14] extended the set of primitives with the digital signature primitive. Compared to the UCSA, we impose weaker assumptions on the protocols, at the cost of remaining within the computational analysis approach. The Dolev-Yao algebra is free, meaning that no two distinct symbols represent the same (real) message. For example, this freeness condition implies the exclusion of commutative operations within the considered protocols. In our approach, we are not restricted by such algebraic constraints. Nonetheless, the UCSA approach can be channeled naturally into the implementation of our approach for decreasing the complexity of the analysis in cases when the classical protocol is a simple protocol built from public key or digital signature primitives.

• III.    Overview of the Approach

We consider classical (non-quantum) protocols and primitives which are run by honest parties on classical computers. We are interested in algorithms which are not efficiently breakable by an adversary using quantum computers. The adversarial quantum computer communicates via classical (digital) links, i.e. its input and output are classical. In Figure 1 the real and the ideal system is shown according to the UC approach of Canetti [5]. Protocol machines P i , i =1,…, n are parties in protocol π. The ideal implementation of the considered cryptographic task is defined by ideal functionality F . The protocol machines and the ideal functionality is (classical) polynomial-time and communicate over classical communication channels. However the adversaries (real adversary A and ideal system adversary (simulator) Sim ) and the interactive environment (distinguisher) Z run quantum-polynomial-time algorithm. Distinguisher Z outputs 1 or 0 if it decides on seeing the real and the ideal system via the total interface (dashed line), respectively.

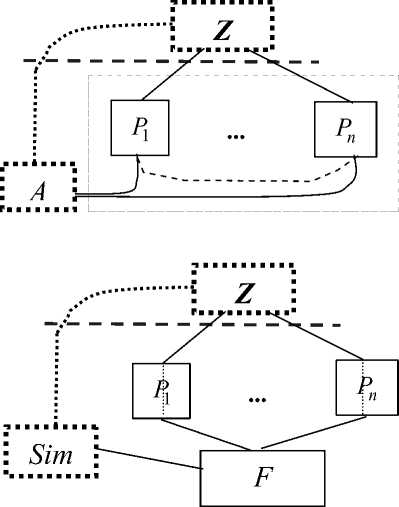
Fig.1. The Real and the Ideal System (Upper and Lower Figure)

Protocol π classical-UC-emulates F if for any adversary A there exists a simulator Sim such that for all environments Z the difference of the probability that Z outputs 1 when it runs the real system and the probability that Z outputs 1 when it runs the ideal system is negligible.

We will rely on the fundamental results of Canetti ([5], [6]) on classical UC-security as well as quantum-UC extensions of Unruh [16]. From the latter work we will apply Unruh’s Quantum Lifting Theorem and Quantum Universal Composition Theorem [16]:

Quantum Lifting Theorem ([16], Th.15) Let π and ρ be classical protocols. Assume that protocol π statistically classical-UC-emulates protocol ρ. Then protocol π statistically quantum-UC-emulates protocol ρ.

Quantum Universal Composition Theorem ([16], Th.13): Let φ, ρ and σ be quantum-polynomial time protocols. Assume that ρ quantum-UC-emulates φ. Then protocol σ ^ρ quantum-UC-emulates φ–hybrid protocol σ ^φ . (Protocols φ and ρ are subroutines of the application protocol σ.)

We propose a hybrid protocol approach for designing UC-secure protocols in post-quantum world. First, we try to produce a statistically classical-UC-secure hybrid protocol. By the Quantum Lifting Theorem of Unruh, this hybrid protocol is also statistically quantum-UC-secure, consequently computationally quantum-UC-secure. If we can realize the ideal subroutines within this hybrid protocol by computationally quantum-UC-secure realizations then by Unruh's Quantum UC Theorem we arrive at a computationally quantum-UC-secure protocol.

Obviously, successful execution of the approach crucially depends on the success of the first step. Our intermediate goal of having a statistically classical-UC-secure hybrid protocol restricts the class of available protocols.

Definition 1 ( class of considered protocols ): The atomic elements of the considered protocols are public identifiers of parties, locally generated random elements (nonces), public keys, secret keys and inputs to the protocol instance. The considered cryptographic primitives (public key encryption, secret key encryption, digital signature) carry out transformations on the concatenations of such atomic elements as well as previous outputs of transformations (ciphertexts, signatures). Protocol messages are concatenations of atomic elements and outputs of such transformations.

A protocol consists of the main algorithm which calls primitives as subroutines. The main algorithm receives the input from and sends the output to the calling layer. The main algorithm manages the run of the protocol: it sends inputs to the primitives (running as subroutines); generates protocol messages where it uses also the outputs of the primitives; transmits messages between parties. We do factorization along cryptographic primitives and substitute them with corresponding ideal functionalities such a way that the resulted hybrid protocol can be simulated with statistical accuracy. If we expurgate all cryptographic constructs (represented by the primitives) from the main algorithm the success of simulation will depend on the (definition of the) ideal functionalities. Intuitively, the messages between the ideal functionalities and the adversary attacking the hybrid protocol should not have any element which cannot be simulated just relying on public information and local randomness by the side of the simulator.

Definition 2 ( fully factorable protocol ): We assume a hybrid protocol σ ^φ ₁ ^…φ _n , where we have factored out all cryptographic primitives into corresponding ideal functionalities φ 1 …φ n , such that the hybrid protocol can be simulated within the corresponding ideal system with statistical accuracy relying just on public information and fresh random elements. For short reference, we will call such protocols (fully) factorable.

The steps of the analysis will be the following:

• 1)  σ ^φ1^…φn   statistically  classical  UC-emulates   G

(Proposition 1 in Sec. 3)

• 2)  σ ^φ1^…φn   statistically  quantum  UC-emulates   G

(Quantum Lifting Theorem, QLT)

• 3)  σ ^φ ₁ ^…φ _n (computationally) quantum UC-emulates G

(Corollary to QLT)

• 4)    ρ quantum UC-emulates φ (assumption)

• 5)  σ ^ρ1^…ρn quantum UC-emulates σ ^φ1^…φn (Quantum

UC Theorem)

1-5) → 6) σ ^ρ1^…ρn quantum UC-emulates G (Proposition 2 in Sec. 3)

When arguing about the quantum security of symmetric key protocols we will make the following assumption which is more or less “standard” throughout the literature:

Assumption 1 : There exists quantum standard-secure PRG.

• IV.    Fully Factorized Hybrid Protocols and Quantum Security

When we look at the description of a protocol which is hybrid in a cryptographic primitive (say in public encryption primitive) the original real transformations are substituted by the ideal one. For instance, a row within the protocol

A → B: A, E pkB ( m )

becomes

A → B: A, E pkB ( m *)

where message m* is fixed (and known even by the adversary).

We assume that all primitives are substituted by their ideal version. We will consider the ideal functionalities of the following cryptographic primitives: symmetric key encryption [13], public key encryption [7] and digital signature [14]. We wish to arrive at the following conclusion: if these ideal functionalities are simulatable with statistical accuracy, then the hybrid of the protocol can be statistically (classical) UC-secure, i.e. fully factorable.

Our argument will be the following. The inputs of the considered transformations are message (payload), key (secret or public) and locally generated random elements. From these inputs, the message and the secret key may cause some trouble for the simulator. The message input will not cause simulation problem in cases if the message is substituted by a fixed message (by the functionality) or if the message is not private information. As for the secret key, if the secret key is known only by the ideal functionality (which ensures its ideal protection) then for the distinguishing party (environment/adversary) the secret key is an unknown random element from the space of keys. In such case, the secret key can be simulated by relying only on local randomness.

• A.    Unconditionally simulatable ideal functionalities

Public key encryption ideal functionality [7]: The core step in the encryption functionality is the ideal hiding of the actual plaintext message from the adversary: a fixed plaintext message is encrypted and sent to the adversary. The encrypted dummy message produced by the ideal encryption subroutine can be simulated with statistical accuracy as only locally generated random elements are needed by the simulator. In case when the adversary corrupts the sending party, the usual rule is that the ideal functionality forwards the ciphertext generated by the adversary, consequently, a black box simulator is trivially able to produce statistically equivalent ciphertext.

Secret key encryption ideal functionality [13]: Here we refer to the ideal functionality of unauthenticated symmetric key encryption in [13, pp. 27-29]. The idea of dummy message encryption for ideal hiding of the message is similar to the case of public key encryption. Let E ( k , r , m ) denote the secret key encryption of message m with secret key k and one-time random element r (mapping E (., ., .) is deterministic). Now consider the simulation of the ideal encryption functionality. Algorithm E is known by the simulator. In the view of the distinguishing party, the secret key used by the functionality is a random sample from an a priori known distribution (typically uniform distribution over the field of secret keys).The simulator chooses an independent sample from this distribution. As a fixed message is encrypted and the simulator is able to generate random sample ( k , r ) with a distribution equal to the one used by the ideal functionality, it is able to simulate the ciphertext with statistical accuracy.

According to [13], IND-CCA2 secure encryption can provide (classical) UC-secure realization for their ideal functionality. By assuming the availability of quantum standard-secure PRG we can construct quantum standard-secure PRP (we return to this issue in the next chapter). Taking into account that PRP security implies IND-CCA2 security relying on quantum standard-secure PRP we achieve quantum UC-secure realization of the unauthenticated secret key encryption ideal functionality.

Digital signature ideal functionality [14]: The concept of statistically unpredictable digital signature was introduced in [14], with the aim to extend the UCSA framework to protocols using digital signatures. If we use such a digital signature then no adversary even a computationally unbounded one with adaptive access to the signing oracle is able to guess only with negligible probability the oracle’s next output (signature) for any input (message). Such a strong signature is needed in [14] to transform the hybrid protocol into an equivalent Dolev-Yao style symbolic one. Strong signature schemes can provide (classical) UC-secure realization for this ideal functionality (see e.g. super-secure signature schemes in [11]).

This ideal functionality is a modification of the ideal functionally proposed earlier by Canetti in [6]. In [14] the adversary is allowed to define the description of a statistically unpredictable polytime signing algorithm S and a polytime verification algorithm V . Successful forging means the creation of a new (message, signature) pair which verifies correctly, instead of the creation of a correctly verifiable pair for a new message as in [6].

Now consider the simulation of the ideal signature [14]. The simulator obtains the description of algorithms S and V from the simulated (black box) adversary. Using local randomness the simulator produces an instance of the statistically unpredictable polytime signature generation algorithm. This step is similar to the one made by the ideal functionality, as the ideal functionality generates and keeps the "signature key" secret. This way a simulated signature becomes statistically indistinguishable from the one produced within the hybrid protocol. Recall, the unpredictability property of S is needed in the symbolic transformation approach. We do not rely on this special property in the simulation of the hybrid protocol.

Our statement on full factorability is as follows:

Proposition 1: Assume a hybrid protocol σ ^φ1^…φn , obtained from a protocol σ, which is a member of the considered class of protocols and where all cryptographic primitives are substituted by corresponding ideal functionalities φ ₁ …φ _n . Assume those ideal functionalities are simulatable with statistical accuracy. If the hybrid protocol is computationally (classical) UC-secure realization of the ideal functionality of the task then it is also statistically (classical) UC-secure realization of the same ideal functionality.

Proof: We have a real system with the hybrid protocol and an ideal system with an ideal functionality G, where G is the ideal functionality for the cryptographic task. We assume, as usual, that the ideal system adversary (simulator) carries out black box simulation. The proof can be broken down to the indistinguishability of individual protocol messages and the corresponding simulated messages. A generic message is an efficiently evaluable, known deterministic function of the outputs of cryptographic primitives and local random bits, where all a priori known parameters are assumed to be incorporated into the function. Accordingly, the simulator is also aware of this function. As the outputs of the considered ideal functionalities representing the primitives can be simulated with statistical accuracy, the simulator will be able to simulate all protocol messages by a statistically indistinguishable way relying only on local randomness.

• B.    Quantum UC-security

In this paper, we are interested in the adaptation of known computationally UC-secure constructions to the quantum environment. Here the following result can be of help to us:

Proposition 2: Assume protocol σ, coming from the class of considered protocols, is a (classical) UC-secure realization of a cryptographic task G . If the cryptographic primitives used in σ are even quantum standard UC-secure, then protocol σ is also quantum standard UC-secure realization of task G .

Proof: Let protocol σ ^φ ₁ ^…φ _n be the hybrid protocol, where all primitives are substituted by their ideal functionalities. By assumption, protocol σ is a (classical) UC-secure realization of a cryptographic task G . The (classical) UC composition theorem implies that the hybrid protocol is also a (classical) UC-secure realization of the task. Now using Proposition 1, it follows that the hybrid protocol is even statistically (classic) UC-secure. By the Quantum Lifting Theorem, this fact implies that the hybrid protocol statistically quantum UC-emulates G . Obviously this fact implies the weaker computational quantum UC-security of the hybrid. Hence, we can apply Unruh’s composition theorem.

Recall we set a double goal in this paper. One of them is to establish computational quantum UC-security of some sets of classical UC-secure protocols. The other goal comes from the practical requirement of efficiency, which further restricts the set of available protocols. Available constructions for believed to be quantum secure public key encryptions lag far behind our efficiency intentions. The case of digital signatures seems worse, for example, the author is not aware of results even on quantum secure constructions for strong signatures. Accordingly, in the next chapter, first of all, we will discuss the problem of the construction of quantum standard-secure symmetric key protocols. The practical importance is that a fast implementation of symmetric key encryption primitives could be based on AES encryption algorithm with appropriate key size as long as we believe that this encryption algorithm can be a practical instantiation of computationally quantum standard UC-secure PRP. We will also consider the extent of cryptographic tasks reachable by relying only on symmetric key primitives.

• V. Quantum Standard-Secure Symmetric Key Protocols

First, we outline the class of cryptographic tasks which become accessible for our approach when we rely solely on symmetric key primitives. This set of tasks we will call lower layer tasks. The distinguishing characteristic of the higher layer is that even legitimate parties distrust each other, as any of the parties may try to deviate from honest behavior. Therefore, the protocol has to force honest behavior.

A task is in the higher layer if in at least one step of the protocol run there exists at least one party such that a non-unique set of potential non-halting actions is available for him with the (expected) honest action included and the party may deviate from the expected (honest) action in an arbitrary way but keep within the set of non-halting actions. (non-halting action means a step which does not contradict to the verification rules of the protocol)

In the classic example, a party may cheat about the outcome of a local coin flipping. In order to avoid any non-wanted advantage at any parties, the protocol has to force honest behavior, leaving just a single non-halting action for the party at any step. Approaching from another perspective, a cryptographic protocol task implicitly or explicitly defines the outcome (gain) for each participant if the rules are followed honestly by the legitimate parties. An honest party accepts this promised gain and does not look for potential ways for getting extra gain probably at the disadvantage of the peer. If in this respect any of the parties is dishonest the task is of higher layer.

Accordingly, in lower layer tasks parties are trustable and they exactly follow the expected honest actions. In such tasks parties running a protocol, the instance has only a common enemy, the network adversary. Recall higher layer tasks are interesting even in case when the network adversary is missing, e.g. all communication links are secure.

The lower layer hosts tasks for securing the communication network: authenticated communication, secure communication, and key exchange/refreshing. Recall, the core higher layer protocols are zero knowledge, bit commitment, oblivious transfer and remote coin flipping. As it is well known, unfortunately, symmetric key cryptography, in particular, symmetric key encryption has a severe drawback with respect to solving commitment problems during simulation ([1]). Recall, the commitment problem in the simulation based approach of security occurs when the simulator, in vain of some information, has to simulate a certain protocol message and the simulated message contradicts to the correct one when the latter turns out later. For example, if the simulator has to simulate a ciphertext without knowing the plaintext and the secret key, it can resolve the commitment problem only if the encryption key is not revealed later on. In accordance, in [13] it is assumed that the environment does not use the symmetric key encryption functionality in such a way that the commitment problem occurs. Recall, bit-commitment functionality has (classical) UC-realization in oblivious transfer hybrid with statistical accuracy, if commitment is unrealizable with a given crypto toolkit then the same is true for oblivious transfer. Recall that oblivious transfer is complete for the task of general function evaluation, therefore it can be guessed that in the world of symmetric key cryptography, realizations of higher layer tasks can be achieved only by relying on powerful trusted third party (TTP), which in theoretical terms means a "trivial" realization. In this world, all parties have to have secure channel to the TTP, which assumes shared secret key between each of the parties and the TTP. Key initialization needs "out of band" method, therefore, the geographic coverage of such TTP is expectedly limited. This disadvantage can be considered as "cost" paid for efficient implementation based on symmetric key crypto. The restriction on geographical coverage can somewhat be relieved by assuming a chain or in general a graph of TTPs, which might allow that even "TTP-remote" users could be parties of the same instance, i.e. a symmetric key analog of the hierarchy of public key certification authorities.

• A.    Construction of quantum standard-secure primitives

The technique of construction: A fundamental question in cryptography is the construction of a primitive from another one (note, such approach resembles the modular design for protocols). Recall, a black-box reduction is an efficient algorithm that transforms an (even inefficient) adversary, breaking any instance p of primitive P , into an algorithm breaking the instance q of primitive Q . Here both the adversary and the primitive P is black box, and p is the (black-box) construction out of q .

We exploit such black box reduction the following way. Assume we have a black box reduction proof for the classical computational security of a construction P . If the underlying primitive ( Q ) is even quantum standard secure then the black box proof implies the quantum standard security of construction P . We use this argument in generation of quantum standard secure PRF and PRP.

Quantum standard-secure PRF: The strongest model of the symmetric key encryption is the (strong) pseudorandom permutation (PRP). For our symmetric key protocols, we need quantum standard-secure PRP. Recall, we assume the existence of quantum standard-secure PRG. The classical construction of Goldreich, Goldwasser, and Micali (GGM) for PRF is a black box reduction of the breaking of PRF to the breaking of PRG. As we assume the existence of quantum standard-secure PRG, it follows that using the GGM's construction we can obtain quantum standard-secure PRF.

Quantum standard-secure PRP: Now we recall the classical DES-based Luby-Rakoff's construction of PRP out of PRF: Let construction PRP_1 and PRP_2 be the construction which uses real random function and PRF components, respectively. Distinguishability of PRP_1 and PRP_2 can efficiently be reduced to the distinguishability of the PRF from the real random function. In turn, distinguishability of PRP_1 from real random permutation (RP) decreases exponentially in the input block size (under polynomial increase in the number of queries) independently from the computational time of the distinguisher. Consequently, if a quantum standard-secure PRF is available then no adversary even with standard quantum polynomial computational resource is able to distinguish constructions PRP_1 and PRP_2, where in turn PRP_1 is not distinguishable from RP for any such adversary. So if PRP_2 would be distinguishable from RP with non-negligible probability, then the same should be the case for the pair of PRP_1 and PRP_2.

• B.    Examples of quantum standard-secure protocols

“Simple protocols” : Computational complexity of guessed to be quantum standard-secure public key primitives is high. If we set aside the requirement of efficiency and we look just at the goal of quantum standard UC-security then for application examples we can consider the “simple protocols” in [7] and [14], e.g. the Needham-Schroeder-Lowe key exchange protocol. For more application oriented example, we recall that among secure routing protocols for ad hoc sensor networks there are simple protocols, e.g. protocol Endaira [17],[18] which uses solely digital signature primitive.

Secure messaging and key refreshing symmetric key protocols: The message of this example is that assuming the availability of computationally quantum UC-secure PRP encryption, key lower layer protocols remain computationally quantum UC-secure: the fundamental results of Canetti-Krawczyk [8] on secure channel and key refreshing can be adapted to quantum scenario. Also, we can extend the set of primitives to the weaker assumption of computationally quantum IND-CCA2-secure encryption.

First, we consider the UC-secure realization of cryptographic task of secure message transmission (SMT) by F AUTH -hybrid protocol. The task of SMT can be realized computational quantum UC-securely by F AUTH -hybrid protocol assuming computationally quantum secure PRP encryption and preset shared keys. The difficulty of the simulation reduces to the following problem: without knowing the secret key and the message we have to simulate the ciphertext, however, sometimes later the message gets revealed and we have to show up a consistent key (so-called simulation equivocality property) . Note, if we had assumed a real random permutation (RP) for encryption then any key would become consistent. However, this fact is inherited also by computational quantum PRP realization in the view of a distinguisher with computational quantum complexity.

By weakening the assumption on the symmetric key primitive, now assume that standard secure encryption (IND-CCA2) primitive is available which is secure against a computational quantum adversary. The related strongest result in (classical) computational context is in [8], where two different approaches were proposed:

• i) . In the first of them, the commitment problem during the simulation was solved by weakening the UC-model with the introduction of the concept of so-called non-information oracle. We do not need such weakening if we assume the availability of the (much) stronger PRP encryption model. (Note the idea of non-information oracle is not complexity specific it can work also in quantum environment.) ii). In the second approach of Canetti-Krawczyk [8],

(strong) UC-secure realization is possible (i.e. without relying on non-information oracle) if we can assume that computationally UC-secure PRG. We could repeat their approach based on quantum standard-secure PRG.

Finally, considering the task of key refreshing in [8], the UC-secure realization uses secret PRF primitive. Quantum-secure PRF primitive is assumed to be available as we discussed it above.

Recall, if we want to carry out our proposed approach for a concrete protocol then according to Proposition 2 first we have to verify the classical UC-security of the hybrid protocol. In the above examples, we could rely on known to be (classical) UC-secure protocols. If this is not the case, the step of hybridization may substantially reduce the complexity of the verification, though the analysis remains computational. The additional strength of the UCSA approach at this step is the complete elimination (of the complexity) of the computational assessment, as it is purely symbolic. At this point, the UCSA approach can be channeled naturally into the implementation of our approach when the target is a "simple protocols" built from public key or digital signature primitives. Note, however, at least to the best knowledge of this author, there is not known ideal functionality for symmetric key encryption which is of Dolev-Yao style and simulatable according to the Canetti's (classical) UC-security approach. Therefore, the analysis of the symmetric key hybrid protocols seems to remain computational.

• VI. Conclusions

In this paper we have examined the question about the viability of efficient cryptographic solutions, if suddenly it turns out that powerful quantum computers start breaking existing cryptographic protocols all over the globe. An even stronger question is that can we do it even in UC-secure way, i.e. keeping provable security guaranties in arbitrary concurrent environment. Based on previous researches in the field we proposed a technique, which supports to give positive answers to the questions posed:

In this paper, we have shown a technique for the assessment of quantum standard UC-security of cryptoprotocols in post-quantum world. The approach covers the "simple protocols" (defined in [7], [14])

extended with symmetric key protocols. In this approach, the key element and requirement for turning from classical to quantum security are the statistical security of the hybrid protocol, which is ideal in its all cryptographic primitives.

For the implementation, we assumed the existence of quantum standard secure PRG. We took into account also the requirement of efficiency which narrows the set of technology to symmetric key protocols and to tasks for securing network communications (secure channels, authenticated channels, shared key refreshing). Fast realization can be based on AES encryption algorithm with appropriate key size as long as we live with the wide belief that this algorithm is secure against a quantum adversary.

When “simple protocols” (by [7], [14]) are analyzed, the symbolic technique (UCSA) can be used for reducing the complexity of the analysis.