On Computing the Edge-balanced Index Sets of the Circle Union Graph F (3, n)

Published Online March 2016 in MECS DOI: 10.5815/ijmecs.2016.03.03

• I.    Introduction

  Graph theory is an important branch of discrete mathematics which regards figure as the research object. B.M.Stewart introduced a theory in 1966 which use the vertices of graph and the label function of edges making the vertices of graph correspond to the edges, through the mapping function and then studies the characteristics and inherent characteristics of all kinds of figure. Its theory can be applied to the information engineering, communication network, computer science, economics and management, medicine and so on. Over the years many domestic and foreign researchers devote themselves to this area, and have access to a series of results.

In 1995, M.C.Kong and others defined the edge-balanced graph and strong edge-balanced graph in reference [1], and put forward two conjectures: Conjecture 1: All trees except s , n is odd, are edge-balanced. Conjecture 2: All connected regular graphs except K are edge-balanced. The reference [2] extends the concept of edge-balanced labeling to multigraphs and completely characterizes the edge-balanced multigraphs, and proves the two conjectures are true in the reference [1], at the same time proves the problem of decide a graph is edge-balanced does not belong to NP-hard. In 2008, Alexander and Harris studied the vertex -balanced index and friendly index sets of the figure in the literature [3-5].

Since 2009, author and her student Juan Lu solved the edge-balanced index sets of chain graph. In 2010, Ying Wang started the research about the edge-balanced index sets of the equal-cycle nested graph [7].From 2010, Hongjuan Tian[8] and others began the study of edge-balanced index sets of the nested graph with power-cycle.

In this paper, we completely determine the edge-balance index sets of circle union graph F(3,n) by using the basic graph and recursive method. The computational formulas and the construction of the corresponding graphs are also provided.

The paper is organized as follows. In Section 2, we give the definitions that we shall consider. The lemmas are showed in Section 3. The main theorem is presented in Section 4. The final Section 5 contains the conclusion.

• II.   Preliminary Results

In graph theory, a graph G is an ordered pair ( v ( g ) , e ( g ) ) consists of vertex set V ( G ) and edge set E ( G ) , together with an incidence function that associates with each edge of G an ordered pair of vertices of G .

Definition 1 In graph G , let: f : E ( G ) ^ Z be an edge labeling function, that is to say, V e e E ( G ) to define f ( e ) = 0 or 1. The edge set labeled 0 or 1 is recorded as E (0) and E (1) , using e (0), e (1) to present the number of E (0), E (1) . According to the edge labeling f , we can define f ⁺ : v ( g ) ^ {0,1} . If e x (0) is more than e_x (1) , f ⁺ ( x ) = 0 , the vertex x is labeled 0; if e x (0) is less than e x (1) , f ⁺ ( x ) = 1 ,the vertex   x is labeled 1;

otherwise, the vertex x is unlabeled. e (0) or e (1) presents the radix number of the edge collection that the edges linked x are labeled 0 or 1. The radix number of the vertex set V (0), V (1) is presented by v (0) or v (1) .

Definition 2 Let : f : E ( G ) ^ Z is an edge labeling function of G . If e (1) - e (0)| <  1, f is considered as an edge-friendly labeling of the graph G .

A graph G is said to be edge-friendly if it admits an edge labeling f such that | e (1) - e (0)| <  1. If, in addition, we also have | v (1) - v (0)| <  1, we call G edge-balanced. An edge-friendly graph could be far from being edge-balanced. To extend the study of edge-balancedness, we introduce the notion of an edge-balance index sets.

Definition 3: EBI ( G ) = {| v (0) - v (1)| : the edge labeling f is edge-friendly } is thought as the edge-balanced index set of the graph G , if there is an edge-friendly labeling f in a graph G .

In other words, EBI ( G ) is the set of values that |v (1) — v (0)| could attain as we go over all edge-friendly labelings of G .

Let ( H , x ) denote a graph H with a specific vertex.

Definition 4: Let (H,x) be a graph with a specified vertex x, then the one-point union graph Amal((H,x),m) is defined by identifying the x-vertex of m copies of (H,x).

Definition 5: Let C_n = { x , v ,,,,, v_m _J be a cycle. We call the one-point union graph Amal (( C , x ), n ) , denote by F ( m , n ), a flower graph.

For simplicity we will denote it by F ( m , n ) . In this paper, we investigate F (3, n ) . Let the vertices of the ith cycle of f (3, n ) be x , vⁱ , v ⁱ , and assume that x is the specific vertex used in the amalgamation.

Throughout this paper,     denote vertices labelled 0, denote vertices labelled 1,       denote vertices without label;           denote edges labelled 0, denote edges labelled 1.

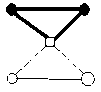
Lemma 2 : For the flower graph F (3, 3), EBI(F(3,3))={0,1}.

Proof : According to the definition of edge-friendly labeling, । e (0) - e (1) | < 1 ,we can get the edge-friendly labeling of the labeled graph by calculation.

By using enumeration, considering all possible edge assignment, we can get the edge-balance index of F(3,3), EBI(F(3,3))={0,1}.

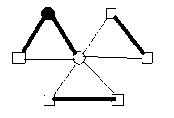
I v ( 0 ) - v ( 1 ) = 1

Fig.1

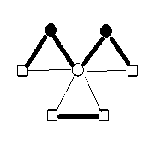
I v (0) - v (1)| = 0

Fig.2

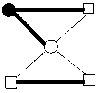
Lemma 3 : For the flower graph F(3,4), EBI(F(3,4))={0,1}.

Proof : According to the definition of edge-friendly labeling, । e (0) - e (1) | < 1 ,we can get the edge-friendly labeling of the labeled graph by calculation.

By using enumeration, considering all possible edge assignment, we can get the edge-balance index of F(3,4), EBI(F(3,4))={0,1}.

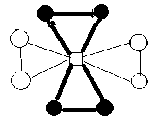
I v ( 0 ) - v ( 1 ) = 0

Fig.1

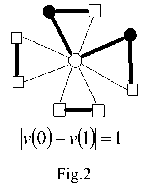
III. Lemmas and Proof

Lemma 1 :   For the flower graph F(3,2),

EBI(F(3,2))={0}.

Proof : According to the definition of edge-friendly labeling, । e (0) - e (1) | < 1 , we can get the edge-friendly labeling of the labeled graph by calculation.

By using enumeration, considering all possible edge assignment, we can get the edge-balance index of F (3, 2), EBI(F(3,2))={0}.

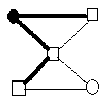
Lemma 4 : For the flower graph F(3,5), EBI(F(3,5))={0,1,2}.

Proof : According to the definition of edge-friendly labeling, । e (0) - e (1) | < 1 , we can get the edge-friendly labeling of the labeled graph by calculation.

By using enumeration, considering all possible edge assignment, we can get the edge-balance index of F(3,5), EBI(F(3,5))={0,1,2}.

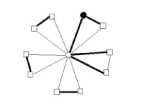
I v ( 0 ) - v ( 1 ) = 0

I v ⁽ 0 ) - v 0) = 1      v ( 0 ) - v ( 1 ) = 2

Fig.1                 Fig.2              Fig.3

I ^{v ( 0 )- v ( 1 )} = ⁰

I v ( 0 ) - v ( 1 ) = 0

Fig.1               Fig.2                Fig.3

| v ( 0 ) - v ( 1 ) = 0

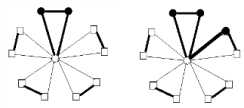
Lemma 5 : For the flower graph F(3,6), EBI(F(3,6))={0,1,2}.

Proof : According to the definition of edge-friendly labeling, । e (0) - e (1) | < 1 ,we can get the edge-friendly labeling of the labeled graph by calculation.

By using enumeration, considering all possible edge assignment, we can get the edge-balance index of F(3,6), EBI(F(3,6))={0,1,2}.

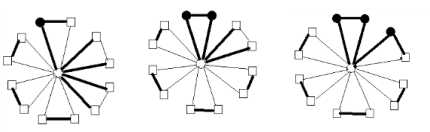
I v ( 0 ) - v ^{( 1 )} = 0       v ( ° ) - v ^{( 1 )} = ¹        v ( ° ) - ^{v ( 1 )} = ²

Fig.1               Fig.2                Fig.3

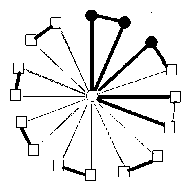
I v ( ° ) - v ( 1 ) = 2

Fig.3

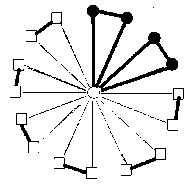
I v ( ° ) - v ( 1 ) = 3

Fig.4

Lemma 6 : For the flower graph F(3,7), EBI(F(3,7))={ 0,1,2,3}.

Proof : According to the definition of edge-friendly labeling, I e (°) - e (1) I < 1 ,we can get the edge-friendly labeling of the labeled graph by calculation.

By using enumeration, considering all possible edge assignment, we can get the edge-balance index of F(3,7), EBI(F(3,7))={0,1,2,3}.

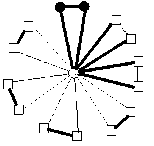
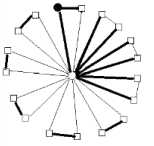
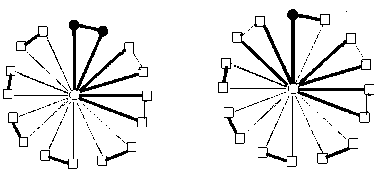
Lemma 8 : For the flower graph F(3,9), EBI(F(3,9))={ 0,1,2,3,4}.

Proof : According to the definition of edge-friendly labeling, I e (°) - e (1) I ^ 1 , we can get the edge-friendly labeling of the labeled graph by calculation.

By using enumeration, considering all possible edge assignment, we can get the edge-balance index of F(3,9), EBI(F(3,9))={0,1,2,4}.

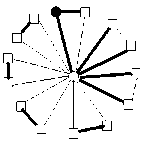
I v ( ° ) - v ( 1 ) = 1

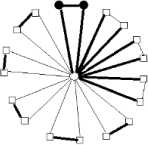
I v ( ° ) - v ( 1 ) = 1

Iv(°)- v (1)=°

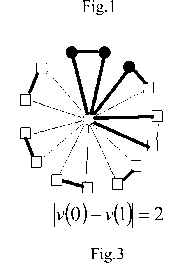
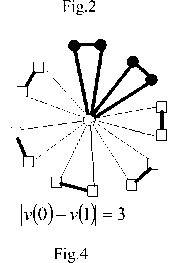
Lemma 7 : For the flower graph F(3,8), EBI(F(3,8))={ 0,1,2,3}.

Proof : According to the definition of edge-friendly labeling, I e (°) - e (1) I ^ 1 , we can get the edge-friendly labeling of the labeled graph by calculation.

By using enumeration, considering all possible edge assignment, we can get the edge-balance index of F(3,8), EBI(F(3,8))={0,1,2,3}.

I v ( ° ) - v ( 1 ) = °

I v ( ° ) - v ( 1 ) = 1

Fig.2

Fig.1

Iv(°)- V(1)=°

Fig.1

Fig.2

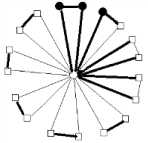
I v ( ° ) - v ( 1 ) = 2

Fig.3

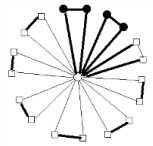
I v ( ° ) - v ( 1 ) = 3

Fig.4

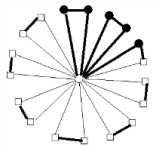
I v ⁽ ° ^)- v ^{( 1 )} = ⁴

Fig.5

Then, we can get the following lemma.

Lemma 9 : When 2 <  n <  9,

EBI ( F (3, n )) = <

{0,1,

{0,1,

. 2 - 1},

, n - ¹ },

n = 2,4,6,8

n = 3,5,7,9

• IV.   Theorem

Theorem 1: For n > 2, n max{EBI(F(3, n))} = - -1.

n

Next we prove {0,1,2,...,— - 1} о EBI ( F (3, n ))

EBI ( F (3, n ) — <

f             n 1

Г^1,2..... 2 - 11

{ 0,1,2.....^ }

if n is even if n is odd

Let A ^ B denote 1 -edge A and 0-edge B exchange their label. Each step is on the basis of the above step. The exchange in turn is as follows.

Proof:

Case 1: Given n >  2 and n is even.

Let v^j v^j (1 <  j <  n ) and xv k (1 <  k <  n ) be 1-edges, and the remaining edges be 0-edges. We call the labeled graph be the basic graph 1. It follows immediately that f is friendly and v — 1, v (1) — n . Then n - 1 _€ EBI ( f (3, n )).

n

Firstly, we prove max { EBI ( F (3, n ))} = — - 1.

In the basic graph 1, we investigate the edge- balance index change when exchanging arbitrary 1-edge and 0-edge. It can be divided five cases to discuss.

• (1)    Any one of the 1-edge xv (1 <  i <  n ) and 0-edge 1 ₂

exchange, v (0) and v (1) have no change. Thus

I v (1) - v (0) 1 remains unchanged.

n

• (2)    Any one of the 1 -edge   v i v ₂ (1 <  i <  —) and

0-edge xvⁱ  in the same cycle exchange, v (0)

constant,  v(1) is reduced. Thus |v(1) - v(0)| is reduced.

n

• (3)    Any one of the 1-edge   v i v ₂ (1 <  1 <  —) and

0-edge except xvⁱ exchange,   v (1)  constant,

v(0) is on the increase. Thus  |v(1) - v(0)|  is reduced.

n

• (4)    Any one of the 1 -edge v₁ v ₂ (— + 1 <  г <  n ) and 0-edge xvⁱ or xvⁱ in the same cycle exchange, v (1) constant, v (0) is on the increase. Thus I v (1) - v (0)| is reduced.

• (5)    Any one of the 1-edge v i v^ ( n + 1 <  1 <  n ) and the same cycle 0-edge except xvⁱ and xvⁱ exchange, v (1) and v (0) are increasing by 1 and 2. Thus I v (1) - v (0)| is reduced.

In summary, It is obvious that the exchanging must bring |v(1)- v (0)| decreases or remain unchanged. Thus v v2 ^ xv       v (1) - v (0)|=n - 2

xv 2 ^ ^v 2 ^v 2²         I v ^{(1) -} v ⁽⁰⁾| = n ^{- 3}

xv k ^^ v k v k        I v (1) - v (0)| — — - k - 1

n-1        n-1 n-1               ,                 , xv22  ^ v2 v22           |v(1) - v(0)| — 0

Thus EBI ( F (3, n )) — {0,1,2,..., n - 1}   ( n is even).

Case2: Given n >  2 and n is odd .

Let v j v j (1 <  j <  n ) and xv k (1 <  k <  n + ¹) be 1-edges, and the remaining edges be 0-edges. We call the labeled graph be the basic graph 2. It follows immediately that f is friendly and     v (0) — 1, v (1) — n + 1 .     Then

-^- e EBI ( F (3, n )).

Firstly, we prove max{ EBI ( F (3, n ))} — n ^{- 1}.

In the basic graph 2, we investigate the edge- balance index change when exchanging arbitrary 1-edge and 0-edge. It can be divided five cases to discuss.

• (1)    Any one of the 1 -edge _xv i (1 <  i <  ^{n + 1} ) and 0-edge 1 ₂

exchange, v (0) and v (1) have no change. Thus

I v (1) - v (0)| remains unchanged.

• (2)    Any one of the 1-edge v^ (1 <  1 <  ^{n + 1}) and 0-edge xvⁱ in the same cycle exchange, v (0) constant, v (1) is reduced. Thus  | v (1) - v (0)| is

reduced.

• (3)    Any one of the 1-edge v i v i (1 <  1 <  ^{n + 1}) and 0-edge except xvⁱ exchange, v (1) constant, v (0) is on the increase. Thus | v (1) - v (0)| is reduced.

• (4)    Any one of the 1-edge v^v¹^ ( n + 3 <  1 <  n ) and 0-edge xvⁱ or xvⁱ in the same cycle exchange, v (1) constant, v (0) is on the increase. Thus

|v (1) - v (0)| is reduced.

n + 3

• (5)    Any one of the 1-edge v i v^ (—— <  i <  n ) and the same cycle 0-edge except xvⁱ and xvⁱ exchange, v (1) and v (0) are increasing by 1 and 2. Thus I v (1) - v (0)| is reduced.

In summary, It is obvious that the exchanging must bring v ( 1 ) - v ( 0)| decreases or remain unchanged. Thus n — 1

max{ EBI ( F (3, n ))} = —.

Next we prove {0,1,2,..., n - 1} c EBI ( F (3, n ))

Let A ^ B denote 1 -edge A and 0-edge B exchange their label. Each step is on the basis of the above step. The exchange in turn is as follows.

v 1 v 1 ^ xv 1

xv₂ ^ v ² v 2

xvk ^ vkvk n-3       n-3  n-3

xv ₂² ^ v ² v ₂ ²

I v (1) - v (0)| = n - 3 | v (1) - v (0)| = n-5

n - 1 - 2 k

Now we only need to prove 0 g EBI ( F (3, n )) . Assume a new label f , Let _xv i (1 <  i <  ^{n - 1}) , v k v k ( n - ¹ <  k <  n ) and xvl, (1 <  j <  n-3 ) be 1-edges, and the remaining edges be 0-edges. Thus | v (1) - v (0)| = 0 . Thus EBI ( F (3, n )) = {0,1,2,..., n - ¹} ( n is odd).

The proof is completed.

V Conclusion

Based on power-cycle nested network graph, using the new designs about the graph, analysis of induction, the edge-balanced index sets of Circle union F(3,n) graph were investigated. we showed the proof of the computational formula, at the same time giving the construction of the corresponding graphs. The resulting work using the same method will be investigated in a future paper.