On Correlation of Р And NP Classes

Published Online April 2012 in MECS DOI: 10.5815/ijmecs.2012.03.03

Whether the issue on those NP-complete problems is really hard to solve, is considered now as one of the key open issues of modern mathematics and theoretical cybernetics. Contrary to readiness of the majority of experts to consider that all NP -complete problems are hard to solve, there is no progress both in proof, and in a refutation of this proposal. Therefore the purpose of the work is an attempt to explain why there was the situation. The theory of NP-complete problem s is constructed for problems of recognition of properties. The problem of recognition L can be considered as consisting of two sets: D i and Y д , where D i – set of all single problems, and Y д – set of problems with the answer "yes", thus Y_gc D i . The form of these problems consists of two parts. In the first part the exposition of conditions of the problem in terms of various components is given: sets, networks, numbers etc. In the second part the question assuming one of two answers "yes" or "no" is formulated. Informally, class of NP-complete problem s is defined by means of concept of nondeterministic algorithm. Such algorithm consists of two stages: guessing and check. At first, under the set single problem I a guessing of structure S takes place, and further, taking into account statements of problem I, check by the determined algorithm which is ended either by the answer "yes" or "no" is carried out. As it is shown in [1], nondeterministic algorithm solves the problem of recognition L , if for any single problem Ie D i two following conditions are met:

• 1.    If Ie Y_g there is such structure S which guessing leads to that the check stage will be completed by the answer "yes".

• 2.    If Ie Y_d there is no such structure S which guessing for I will lead to that the check stage will be completed by the answer «no».

The concept of polynomial "checkability" [1] allows actual selection of a class of NP-complete problem s, and in addition, "checkability" for polynomial time does not attract decidability of the problem of recognition for polynomial time. The problem of recognition L is called NP - complete if Le NP and any other problem L^/ from this class is reduced to L polynomially.

In his study [2] titled «Complexity of procedures of a conclusion of theorems», Cook has proven that one specific problem from class NP named “satisfiability” possesses the property that any other problem from class NP can be reduced to it for polynomial time. Let’s prove, that the statement is incorrect.

• II.    FORMALISING OF THE “satisfiability” PROBLEM

Wherexf = J _L’            .

• 1    [ xi at - f = 0

Operations v and л are Boolean and model elementary logical expressions: v - "OR"; л - "AND". For any binary gang x = ( x 1 , x 2 ,.., x n ) the function accepts one of two possible values: unit or zero. The “satisfiability” problem consists in the answer to the question: whether there is a gang of values of the variables х = ( _x 1 , _x 2 ,,,, _x n ) converting function f to unit.

• A.    Problem setting and solution

For estimation of satisfiability or an unsatisfiability of Boolean functions let’s, at first, consider properties of unsatisfiable functions and methodes of their obtaining.

• B.    Properties of unsatisfiable Boolean functions

Let's introduce concept of minimum conjunctive form Fminf of an arbitrary Boolean function f of two variables with a minimum number of disjuncts r at which Fminf accepts value “false" for all possible gangs of the function. For this purpose let’s consider a bipartite graph G22 of a view shown in Figure 1, which one part is formed by variables (a, b), and the second is formed by variables ( a , b ) . In the graph those nodes are connected by edges which do not form inverse pairs of (a, a) type.

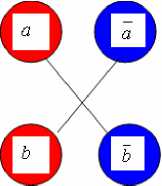
For inconsistency origin in a Boolean function, it is necessary that both variables ( a , b ), and ( a , b ) were present. The perfect matching in graph G 22 provides all possible additions of combinations of variables which can be connected among themselves by an edge as these nodes in the graph are not inverse. Addition of disjuncts comprising variables ( a , b ) and ( _{a ,} b ) by disjuncts which comprise the variables stipulated by a perfect matching in the graph G ₂₂, will allow the minimum form to receive:

F £^In = ( a V b )( a V b )( a v b )( b v a ) . (1)

Let's present a Boolean function f in the form of sliced graph G where each variable in disjuncts corresponds to graph node, and each slice or a tier correspond to disjunct in which nodes are not linked among themselves.

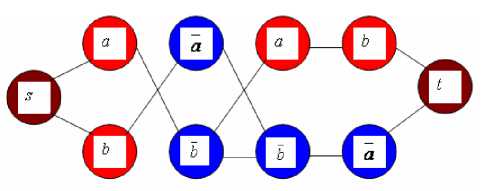
Connections between nodes of tiers are carried out as follows. The node i , corresponding to variable Х i of an arbitrary tier, is connected to all nodes of a following tier, except nodes i^* , corresponding to a variable Х _i .

Let’s name nodes i and i^* as inverse nodes of the graph. As it will be visible further, the arrangement order of tiers in graph G for the solved problem is of no concern. Let’s introduce also two dummy nodes s and t which are linked to all nodes of the first and last tier of graph G, accordingly. Then the graph of the function (1,) looks like in fig. 2.

Clearly, that if in graph G of an arbitrary Boolean function f there is a path from node s to t which does not include inverse nodes, there is a gang of variables on which function f accepts value "true". Let’s assume, it is obtained the path from s to t in the graph G which does not contain inverse nodes ( s, i, j, … k, t ). A variable either Х i , or Х _i corresponds to each node there, i.e. we can put in correspondence paths ( s, i, j, … k, t ) to a gang of variables ( _{X i , X j ,... X k} ) among which there are no contradictory, that ensures absence of inverse nodes in the path. Therefore, we can easily specify a gang of variables at which all gang will consist of units. However, as variables in the gang were used from each tier of the graph, it means that there will be unit at every disjunct and function f accepts value «true» for this gang of variables.

Thus, if function f accepts value "false" for all gangs, then there is no path from node s to t in the graph of function G which does not include inverse nodes, that is clear on the graph presented on fig.2. Considered conjunctive forms possess the important property, v , consisting in that the modification of a sign of inversion in an arbitrary literal leads to that changed function F f , becomes satisfiable. It is easily possible to be convinced of that directly parsing graph G 2 f of the function F^min 2f from which it is clear, that the modifications defined by property, v , will lead to occurrence of the paths in the graph which are not containing inverse nodes and, therefore, function f will become satisfiable. If we consider functions F nf with arbitrary number of variables and with number of variables in disjunct not less two, it is possible to present such functions in the form of association of two graphs of bipartite graph G _n f , see fig.3, in which nodes of one part correspond to variables ( О 1 , О ₂,..., X n ) , and for the second part - ( X 1 , Х 2 ,..., X n ) (subsets of binary graphs G^ f in which links between nodes corresponding to variables ( х 1 , х ₂ ,..., x n ) ^and (F 1 , F2 ,..., F , ) are defined by perfect matchings in graph G nf ) .

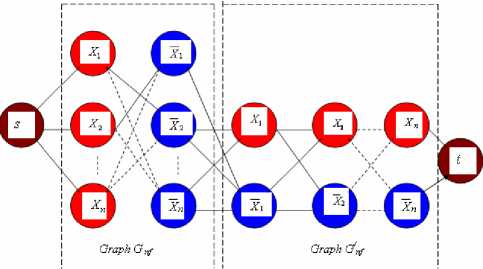
Figure.3 . The graph which generates functions F nf

F m X a X₁ va 2 X , v_yq X ) / ;X i / 2 X 2 V .. / X ) ) ( X₁X₂.X v X 1 X 2 ..X ) =

= X_xX 2. .X , / X i / 2 X : v .. v P X , ) v X i X,„.X , ( a X a X 2 v.-vcX ) =

J V i) =⁽ a X I ^va X : ... a X ). (2)

As the “satisfiability” problem can be considered as the cover problem on a Boolean, then using a Boolean function let’s construct a matrix B in which variables ( x 1 , x 2 ,..., x, ) and (x 1 , X 2 ,..., X , ) there correspond to columns, and disjuncts of a Boolean function correspond to lines. Generally, the number of columns in a matrix B equal to 2 n , and a number of lines is equal to number of disjuncts m in a Boolean function.

For example, for a B oo lean fun ct ion F _nJ = ( X ₁ v X ₂ v X 3 v X 4 ) ( XT 1 v X 2 v X 3 v X 4 ) ■ ■ ( x ₁ v XT з X x ₂ v F 4 X x 3 v XT 1 X x ₁ v XT 2 )

The matrix B will look like

1 2	Х 1 1 0	Х 2 1 0	Х 3 1 0	Х 1 0	Х 1 0 1
B = 3	1	0	0	0	0
4	0	1	0	0	0
5	0	0	1	0	1
6 L	1 et’s	0 name	0 the	0	0 columns

to

Х 2 Х 3 Х 4 000 111 010 001 000 100 corresponding

variables X i and X i in a matrix B as inverse. If in a matrix B there is a cover of lines by units which belongs not to inverse columns, it means that function f is satisfiable, and if such cover is not present it is unsatisfiable.

And so, let the Boolean matrix B is set with 2n columns and m lines where m corresponds to number of disjuncts in a Boolean function f. Let’s define columns using a vector (X1, X 2,..., X,, X1, X2,..., X, ) , and lines - using the vector M = {p1, p2, .., pm}. Let’s call as cover Q of lines M such set of graphs B which covers all lines of M with units. For definition of all covers of the matrix we will use an algebraic method of obtaining the reduced systems of simple implicants of Boolean functions using table of prime implicants. If to consider each column from a population (X1, X 2,..., X,, T1, T2,..., F, ) as a «prime implicant» cover population of lines M = {p1, p2, ..., pm}, and each line pI as a gang of the variables covered with prime implicants, then it is possible to present a matrix B as table of prime implicants of Boolean function f. At such interpretation of a matrix B, it is possible to note for each line pi a disjunction of columns b,, cover considered line, as follows:

dp i = ( X l ¥ O e v......)

… … … … … … …. (3)

dp m = ( х_Р v X t v......).

Conjunction of disjunctions (3) for all lines p ₁, p ₂, ..., p m oJ the matrix B forms conjunctive representation of the matrix B comprising all covers of a population of lines M :

Removing the parentheses according to distributivity laws, we receive disjunctive representation of the matrix B forming the list of all possible covers of a population of lines M = { p ₁, p ₂, ., p m }. For clearing up of existence of a cover, let’s take a principle of superposition in the Boolean algebra based on following equalities:

/у с 1 y ° ²   y " j — /у ст 1_1 y ° ²   у о Л By⁶' у ст ² _ 1 y™L

f/I У ⁰ "¹ У ° ² y ⁰²! — ^I У ⁰ "¹ — П У ^ ² У ° ’к / f i У ^{6 1} У ^ ² — П У ⁰² к/ \/ ^J ( ^X 1 , ^X 2 ,... X , ) = ^J ( ^X 1 = °> ^X 2 ,..., X , ^{) v J} ( ^X 1 , ^X 2 = 0^-..X , ^{) v} ... ^v v J / ( X 0 ¹, X C ²,...X0- =0 ). (5)

Without breaking the principle of superposition (5), it is possible to present an initial Boolean function in the form / ( x 0 ¹,..., X C ) = J , ( X C ¹, :, X C ) ^v J 2 ( X 0 ¹,..., X C ) ^v . ^v /, ( x 0\_ X C ) ^v J , + 1 ( x с ¹,..., X 0 ) ^v J , '+ 2 ( x 0 ,..., X C ) ^v ^ ^vv j 2, ( x c ¹,., x c ) , (6)

^Where / ■( X 0 ¹,...,X C ) = X , J ( x . " ,..., X C ) ; / ' ( x 0 F..., X C ) = o ; J ( x 0 ,..., x C ) .

Let's rewrite a relation (6) in the form J ( X 1 ^{0 1},..., X- C ) = ( X 1 v X 2 v ... v X, ) J ( X 1 ^{0 1},..., X C ) v ... . (7) v ( X 1 v X 2 v ... v X , ) J / ( X C ¹,..., X C )

As follows from (7), in order that this Boolean function was identically equal 0 for all gangs of variables, it is necessary that functions J , ( x ^{0 1} ,..., x, ^{0 2} ) and J , ' ( X ^C = ¹,..., x ^c ) were equal to ( X , ■ X 2 ■ ... ■ X , ) and ( x ₁ ■ X ₂ ■ ... ■ X , ) , accordingly and, therefore, the relation (7) is degenerated into a relation (2), as was to be proved.

In a disjunctive normal form, expression (2) looks like

Let's designate set of single “satisfiability” problems S. It is possible to divide the set into two subsets S+ - a subset of satisfiable single problems and S- - a subset of unsatisfiable single problems, when S = S + иS.

Any unsatisfiable Boolean function should comprise, in explicit or implicit form, Fminnл and if it comprises Fminnf implicitly, it can be always transformed to the form (2) or (8). For an arbitrary Boolean function with n variables it is possible to construct some minimum false forms, which number is actually defined by number of perfect combinations in graph G/пf and as they can be present at a Boolean function and in various combinations it is possible to make a conclusion that the potency of set of unsatisfiable single problems S- is exponential-fold than potencies of a set of satisfiable single problems S + i.e. the inequality is true

|S - |>>|S + | (9)

As shown in studies [1-6], polynomial reducibility of the problem of recognition I 1 to the problem of recognition I 2 means availability of function f which transforms a subset of problems D i 1 into a subset of problems D i 2 ( D i 1 → D i 2 ), on the basis of some rule П i and, thus, satisfies to two conditions:

• 1 .    f – is calculated by a polynomial algorithm;

• 2.    For all I ∈ D i I ∈ Y д 1 , when and only when f ( I ) Y ∈ д 2 .

Let's consider three subsets of problems { I i }; { Z i }; { C i }. Let the problem I- NP-is complete and represents the universal problem, and problems Z and C are also NP -complete then, according to that as the class of NP-complete problem s is introduced, they should be reduced polynomially one to another and, thus, if the polynomial algorithm for one of them is discovered, there should be polynomial algorithms for all single problems { I i }; { Z i }; { C i }. As the universal problem can appear any of NP -complete problems, all following reductions should be true

{ I i } → { Z i } → { C i }; (10) { I i } → { C i } → { Z i }; (11) { C i } → { I i } → { Z i }; (12) { C i } → { I i } → { Z i }; (13) { Z i } → { C i } → { I i }; (14) { Z i } → { I i } → { C i }. (15)

In addition, there are rules П iz and П zc which permit to reduce problems I p → Z p and, thus, { I р } ∈ Y дi and problems Z p → C p and, in this respect, { Z р } ∈ дz , i.e. transformation rules П iz and П zc satisfy to conditions of polynomial reducibility 1 and 2. Let’s consider a case similar to (9) when structures S are such that they generate set of single problems { Z } which by its potency exceeds set of single problems { I }. If the subset { I } contains n single problems, and sets { Z } and { C } contain n + k single problems each, then for some subset of problems { Z_{n+ 1} , Z_{n+ 2}, …, Z_k } we cannot put in correspondence any problem from { I i }. Therefore, the reductions (10) and (11) are possible for all problems, and reductions (12), (13), (14) and (15) are possible not for all problems, they are not possible for problems { С n+ 1 , С n+ 2 , …, С k } and { Z n+ 1 , Z n+ 2 , …, Z k }, and, it means in this case, that the statement about all NP -complete problems are polynomially reduced to each other, is not fulfilled. Thus, the concept of the NP-complete problem requires an improvement. In order that the NP-complete problem was universal and reduced in any directions within a class, it is necessary that there was a one-to-one correspondence between all single problems { I_i }; { Z_i }; { C i }, i.e. for any pair of single problems there should be the direct and inverse polynomial reduction defined by conditions 1 and 2.

Thus, if we have subsets of problems { I i }; { Z i }; { C i }, and the potency of set of single problems { I i } differs from a potency of sets of problems { Z i } and { C i }, then to prove that some problem I is NP -complete, it is not enough to show that any single problem { I i } is polynomially reduced to set of problems { Z_i } and { C_i }, i.e. conditions 1

and 2 are satisfied as it was made in the proof of NP-completeness of the “satisfiability” problem in Cook's and Carp’s studies, but thus it is necessary to show, that there are also problems { І n+ 1 , І n+ 2 , …, І k }, which are polynomially reduced to problems { С n+ 1 , С n+ 2 , …, С k } and { Z n+ 1 , Z n+ 2 , …, Z k }, and "checkability" of these recognition problems should remain possible for polynomial time.

Let's show, that the “satisfiability” problem is not universal. So, Cook has proved universality of the “satisfiability” problem at first. After one NP -complete problem has become known, process of the proof of NP-completeness of the problem A becomes simpler. To prove NP-completeness of problem А ∈ NP it is enough to show, that any known NP- complete problem A ^/ can be reduced to А as property of polynomial reducibility is transitive i.e. if the problem A for polynomial time is transformed to the problem B and if B is transformed to C for polynomial time , then A is transformed to C for polynomial time . First , under the circuit NP- completeness of six primal problems has been proved: «three-dimensional combination»; "partition"; «vertex cover", "Hamilton cycle";"complete subgraph». As they were first problems which have been introduced into a class of NP- complete ones after the “satisfiability” problem, the proof of their NP-completeness was reduced to introduction of rule П on which basis for some arbitrary “satisfiability” problem y ∈ Y structure S possessing property ν if and only if y accepts value “true”. For example, for a «vertex cover» problem, graph G has appeared as structure S , and property ν consisted in that graph G has a vertex cover with number of elements no more K , if and only if a gang of disjunctions, С = { с ₁ , с ₂ ,..., c _m } is fulfilled defining the arbitrary single "3-satisfiability" problem. Generally, the «satisfiability» problem represents some set Y of single problems defined by various modes of set up of logical function. It should be noted that during proof of NP-completeness of all six enumerated problems the arbitrary single problem is selected at first у ∈ Y and then under the problem graph G is built for polynomial time. That graph should contain interesting structure which possess the necessary property, ν , only if the logical function corresponding to the single problem, accepts value «true». As graph G can be arbitrary, we will solve some single problem z ∈ Z where Z is the set of problems generated by usage of various types of graphs G .

During solution of the arbitrary NP -complete problem of graph theory there is an inverse problem: arbitrary graph G is set, and then it is required to determine, whether the graph G possesses structure with property ν , or not.

This brings up the questions: what single problem (y) from set of single “satisfiability” problems Y corresponds to the problem z ∈ Z generated by graph G, and whether for all problems Z there is an inverse correspondence, and if such correspondence exists, how to construct it under the initial graph and whether will be this construction polynomial or not?

In the theory of NP-complete problem s [1-5] there are no answers to these problems yet, and property of inverse polynomial reducibility of single problems y ↔ z is by default transferred to sets Y and Z .

Let's show that if consider «satisfiability» problem as universal the circuit according to which all list of NP-complete problems is actually obtained, does not ensure existence of correspondence of problems y ↔ z and their polynomial reducibility to each other. Let’s consider correspondence of problems y ↔ z, in which we should assign a corresponding «satisfiability» problem to structure S possessing property ν, and the problem accepts value “true” when and only when structure S possesses property ν.

Let rule П is introduced, on which basis under some arbitrary «satisfiability» problem y ∈ Y structure S has been constructed which possesses property ν in then and only then when y accepts value «true». It should be noted that this approach has been used for proof of NP-completeness of all six principal NP -complete problems.

Generally, in order to justify a possibility of that correspondences y ↔ z at the proposal that the «satisfiability» problem is NP - complete, cannot take place and thus the problem z cannot be transformed to the initial problem y for polynomial time it is enough to show it by the example of one of six principal NP -complete problems. Let’s consider this by the example of a «vertex cover» problem.

Let's mention the rule П which was used for the proof of NP-completeness of the «vertex cover» problem in the study [1]. Let U = { u ₁, u ₂,..., u_n } and C = { c ₁, c ₂,..., c_m } define the arbitrary single "3-satisfiability" problem. Let’s specify graph G ( V, E ) and a positive integer K ≤ | V | such that G has a vertex cover with number of units no more K when and only when a gang of disjunctions C is fulfilled. For each variable _{u i ∈} U there is a component T_i = ( V_i , E_i ) of truth values gang (where V_i = { u_i , u_i } , E_i = {{ u_i , u_i }} ), i.e. T _i is pair of the nodes connected by an edge, thus any vertex cover should cover an edge from _Ei , therefore it should contain at least one node u _i or u _i . For each disjunction, _{c j ∈} C there is a component of satisfiability check S_j = ( V_j ^| , E ^| _j ) consisting of three nodes and three edges connecting them and forming a triangle:

V j ^| = { a 1 [ j ], a 2 [ j ], a 3 [ j ]},

E ^| j = {{ a 1 [ j ], a 2 [ j ]},{ a 1 [ j ], a 3 [ j ]},{ a 2 [ j ], a 3 [ j ]}}.

Any vertex cover should contain at least two nodes from Vj| to cover all three edges fromE|j . Linking edges are the single part of a construction depending on what literals enter into disjunctions. We put in correspondence three literals xj ,lj, pj to each disjunction cj ∈ C containing those literals. Then the linking edges which are starting fromSj are set as follows:

E ^| _j ^| = { a ₁[ j ], x_j }, { a ₂[ j ], l_j }, { a ₃[ j ], p_j }}.

Construction of the single «vertex cover» problem is ended if to suppose К = n +2 m and G = ( V , E ), where nm nm m

V = ( U v ) U ( U V j ); E = ( U e ) U ( U E j ) U ( U E j ). i = 1 j = 1 i = 1                 j = 1                 j = 1

Let's consider a Boolean function f = ( u ₁ ∨ u ₂ ∨ u ₃)( u ₁ ∨ u ₂ ∨ u ₃)( u ₁ ∨ u ₂ ∨ u ₃)( u ₂ ∨ u ₁ ∨ u ₃) ⋅                 (16)

⋅ ( u ₃ ∨ u ₄ ∨ u ₅)( u ₃ ∨ u ₄ ∨ u ₅)( u ₃ ∨ u ₄ ∨ u ₅)( u ₃ ∨ u ₄ ∨ u ₅).

According to described procedure П , graph G 1 = ( V 1 , E 1 )

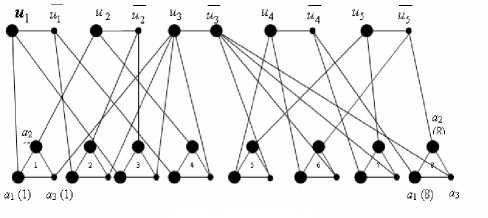
Figure.4. Graph G ₁ = ( V ₁ , E ₁)

for the function will be of the form shown on fig.4. Thus the number of the nodes forming the minimum cover in the graph should not exceed K = n+2m=5+16=21. Let’s show that function (16) is unsatisfiable on any gang of variables. For this purpose let’s consider function of two variables f = ( u1 ∨ u2 )( u1 ∨ u2 )( u1 ∨ u2 )( u2 ∨ u1 ) (17)

It is easy to check up, that function (17) is unsatisfiable on any gang of variables. Let’s transform (16), having added into each parenthesis a variableu3 and having increased function (17) by a multiplier(u3 ∨u4 ∨u5)(u3 ∨u4 ∨u5)(u3 ∨u4 ∨u5)(u3 ∨u4 ∨u5). It is easy to see, that thus we will receive function (16). Such adding of variables leads to that the variable u3 will accept value "false" in any gang of the validity which fulfills conditions (16). Therefore disjuncts containing by two variables in (17) will be equivalent to disjuncts substituted them, therefore, function (16) is satisfiable when and only when function (17) is satisfiable. Considering that (17) is unsatisfiable on any gang of variables, the function (16) is unsatisfiable on any gang of variables, too. From fig. 4 it is clear that there is no the cover in graph G1 consisting of 21 nodes that is well agree with that there is no gang of variables on which function (16) would be satisfiable. But, it is easy to specify a cover on graph G1 = (V1, E1) consisting of 22 nodes; these nodes are shown on fig. 4 as boldfaced, thus it is easy to check up, that the current cover in graph G1 is minimum. There is a question, whether it is possible to construct such Boolean function for graph G1, adhering to rule П, that it would be satisfiable only in that case when the minimum cover in graph G1 did not exceed 22 nodes. It is obvious, that such function should contain function (16), and this part of function will ensure, that there is no cover less than 22 in graph G1, and a number of disjuncts which is necessary to have in its structure in order that rule П was fulfilled, should be equal to (22-5)/2=8,5. That is impossible, as such function, at first, will be unsatisfiable for all possible gangs as it includes function (16), and, secondly, the number of disjuncts in function cannot be fractional. If trying to realize reconversion for an arbitrary graph considering rule П, we should have the number of disjuncts in the single “satisfiability” problem equal to m = (K-n)/2, i.e. if K-n is odd, the number of disjuncts will be fractional number. Thus, there is no such «satisfiability» problem which function constructed on the basis of rule П, considered in the study [1], would accept value «true» when and only when the number of nodes in a cover of graph G1 does not exceed 22. It is possible to construct so much such examples, how many unsatisfiable functions exist, i.e. exponentially large set. It is necessary also to note, that even if a conversion exists, after performance of the conversion the number of true propositions can appear exponentially large, and only one true proposition possessing some propertyγ will satisfy to property ν of initial graph. So, it is shown in the study [6], that if f is the Boolean function constructed by graph G = (V, E) in the form of product of disjuncts (Vi ∨Vj) where {Vi} ∈0,1}, i = 1,n j = 1,n i ≠ j and in the same time every disjunct (Vi ∨Vj) corresponds to an edge (Vi, Vj) all gangs of variables {Vi, Vj} for which it accepts value «true» correspond to vertex covers in graph G = (V, E). It follows that for enumeration of all vertex covers of graph G = (V, E), it is necessary to define those systems of values of variables {Vi, Vj}, at which expression is true

f ( V 1 , V 2 … V n )=1, (18)

In order to determine these systems of values of variables { v i ,v j }, it is necessary to reduce the left part (18) to minimum DNF (a disjunctive normal form) removing the parenthesis and using the law of absorption. Such form is unique in view of logical negations in (18) are absent. Let’s demonstrate this by an example of graph G presented in fig.5.

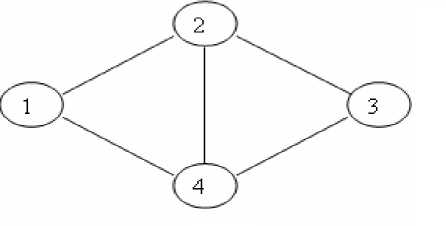
Figure.5. Graph G

Boolean function for the graph will look like:

f = ( V 1 ∨ V 2 ) ( V 2 ∨ V 3 ) ( V 3 ∨ V 4 )(V 2 ∨ V 4 )( V 1 ∨ V 4 )

=( V ₂ ∨ V ₁ V ₃) ( V ₄ ∨ V₁ V ₂ V ₃) = V ₂ V ₄ ∨ V ₁ V ₂ V ₃ ∨ V ₁ V ₃ V ₄ .(19)

Apparently from (19), as a result of disclosure of parenthesis and collecting terms, we have obtained the complete enumeration of vertex covers of graph G (fig.5). They are subsets of nodes: {2, 4}; {1, 2, 3}; {1, 3, 4}. Generally, function (18) contains exponential number of true propositions as it does not contain logical negations and, thus, if we find the minimum cover, the expression should satisfy to the property γ consisting that disjunct which corresponds to the minimum vertex cover, should be of minimum length, i.e. contain the least number of variables {Vi}. The conversion can be easily applied to graph G1, but at the same time for definition of property of the graph v, performance of exponential number of steps is required. If to assume nevertheless, that in this case there is a polynomial algorithm for the conversion, it would mean, that the «vertex cover» problem is solvable for polynomial time that contradicts the proposal that NP-complete problems are insoluble for polynomial time. Therefore, if direct and inverse conversions are exist, reconversion can be exponential, instead of polynomial.

It means, that if to assume in example (10-15), that І is the «satisfiability» problem, then we basically can put in correspondence for problems { С n+ 1 , С n+ 2 , …, С k } and { Z_{n+ 1} , Z_{n+ 2}, …, Z k } the problem { І n+ 1 , І n+ 2 , …, І k } such that all reducibilities (10-15) are satisfiable for polynomial time, but upon that, "checkability" of the problem of recognition I p>n can require exponential number of steps.

And so, if to select the «satisfiability» problem as the universal problem we can face a situation of impossibility of polynomial reducibility of some subset of problems in a class of NP-complete problem s. It happens because Cook's proof is carried out for set of single problems of satisfiable Boolean functions S ⁺ for which polynomial reducibility is simply enough justified using a Turing machine as the calculator model, and upon that the set of single problems S ^- of unsatisfiable Boolean functions is completely eliminated from the analysis, which potency essentially exceeds a potency of set S ⁺.

III. Inference

So, the class of NP-complete problem s is introduced improperly as the «satisfiability» problem cannot claim for a role of the universal NP -complete problem. Also, the issue on existence of at least one NP -complete problem remains open as universality of any problem from NP class, except the «satisfiability» problem, has not been proved, and they have been included in list of NP -complete problems only on the basis of reducibility of the «satisfiability» problem to them.

Upon that, it is actually possible to divide all known set of problems which are called NP-complete into subsets within which polynomial reducibility between all problems of the subset is possible, for example: vertex cover, maximum independent set and a complete subgraph in the graph. However, most likely, reducibility between subsets can take place only for separate single problems [7]. The problem of polynomial reducibility between subsets can appear algorithmically insoluble problem. Therefore, while if we cannot answer a question whether there is at least one universal NP-complete problem then the question if Р=NP or not, is simply premature and has no sense yet. It is necessary to note also, that all conclusions made in the theory of problems from class NP on the basis of the proposal on "total" polynomial reducibility in a class of NP-complete problems, can appear incorrect if the problem of existence of a universal problem appears insoluble.