On Maxima Distribution of Full Differentials and Linear Hulls of Block Symmetric Ciphers

Published Online November 2013 in MECS DOI: 10.5815/ijcnis.2014.01.02

This paper deals with a new methodology of index evaluation of provable security in block symmetric ciphers [1], according to which the properties of block symmetric ciphers can be evaluated on the basis of studying properties of their reduced models.

Here we want to remind one of the central theses of this methodology which is formulated as a statement:

All modern block ciphers 1 after a certain number of cycles independently of those used in S-blocks ciphers (here we don’t mean their degenerated designs) acquire the properties of random substitutions, i.e. according to their combinatorial indexes (the number of inversions, increases and cycles) as well as according to the laws of transition table distribution of XOR differences (full differentials) and the distribution laws of bias linear approximation tables (linear hulls) they repeat the corresponding indexes of random substitutions. As a result the maxima values of full differentials and linear hulls meanings can be determined by calculations from the formulas for the distribution laws of transition probabilities for XOR ta- bles and bias tables of linear approximations of appropriate random substitutions.

Herewith, the test of random indexes of large ciphers can be performed on the basis of the development and further analysis of random indexes of reduced models, permitting to make calculating experiments in acceptable (real) term.

This result is tested on a great number of reduced and large models of many modern ciphers [2-10 and others].

The experiments made however are tied to the limited set of encryption keys. Nevertheless, on the basis of these results the conclusion was made that cipher security indexes can be determined not by the averaging method over the set of keys but on the basis of maxima determination of differential and linear probabilities for any (one) arbitrarily taken cipher key.

We also recall that using this approach the evaluation of block symmetric cipher security indexes is proposed to do not with the help MADP (Maximum Average Differential Probability) and MALHP (Maximum Average Linear Hull Probability), as it is done in a great number of publications, but with the help of AMDP (Average Maximum Differential Probability) and AMLHP (Average Maximum Linear Hull Probability) which, as shown in paper [11] are more suitable to the problem solved.

In this paper we want to substantiate the validity of the conclusion, already presented in a number of works [2-10] that the block symmetric ciphers security against differential and linear attacks really can be determined not by the averaging method over a set of keys but on the basis of maximum determination of differential and linear probabilities for any (one) arbitrarily taken cipher key permitting too convince that maximum values of full differentials and cipher linear hulls coincide with the corresponding indexes of random substitutions.

The general approach to solving this problem is to study the behavior of cipher transformation on the whole set of cipher keys. Experimentally this approach is based on the evaluation with the help of computing experiments the maximum values of full differentials and linear hull biass for reduced cipher models for the whole set of cipher keys (the reduced cipher models permit to do it) and the determination of maximum experimentally obtained values and their number for the whole set of differential and substitution linear table as the ciphers themselves are considered.

Mathematically, this problem casts to the maximum distribution study on a great number of independent random values.

This paper poses the problem of determination of the greatest possible values of transitions among a great number of table XOR differences and biasess tables of linear approximations of small cipher models for the whole set of encryption keys.

The first part of the paper gives theoretical foundations, which are the basis of determination of the maxima distribution laws of a great number of random independent values which are concretized for the distribution laws of independent values: Puasson and normal. The second part gives computational experiment results on the determination of distribution laws of maxima transition tables of full differentials and bias maxima of table linear approximations of reduced cipher models on an example of a new Belorussian cipher and cipher Kalina. At the end of the paper the discussion of the results obtained is given.

• II.    DISTRIBUTION OF MAXIMUMS

First of all we will be interested in mathematical aspects of solving the problem set.

Today, as it is turned out, there is a developed mathematical tool which solves this problem theoretically. We mean the paper [12] which has the appendix in which there is an appropriate material which we will use.

In the first part we will give our appendix translation from the paper which contains theoretical data which constitute the essence of the developed approach. The material of this appendix will be the basis on which we will build and validate our results. Further the translation itself of the part the appendix from the paper [12], which has the same name with this part of paper, is given.

Consider the case when all the values of the large number of independent random variables x have just the same distribution. We will consider that their distribution densities decrease exponentially at large meanings of x. Denote the number of such values 2 ^Y and use the model of integral distribution for every variable D ( X ) as:

D ( X ) = 1 - e ^- f ⁽ X ) (1)

with f ( X ) - function which grows sub-exponentially. From order statistics [13,14] it is known that integral distribution of maximum number of variables is the product of the integral distributions of these variables. Thus we have:

a - X

D max ( X ) - e - e b

This distribution is well studied in the theory of probabilities, as it is marked in [12] and is known as the extreme values distribution, Fisher-Tippett distribution or log-Weibulla distribution [13,14]. The corresponding density is depicted in fig. 1, taken from [12]. Its peak is a and its width is proportional to b . This distribution has mathematical expectation μ ( X ) = a + bγ с γ ≈ 0,58 and deviation ( x ) = -^ b ~ 1,3 b . Notes that the validity of ex- 6

pression (3) depends on the quality of linear approximation f ( x ) near the point ( а ,0).

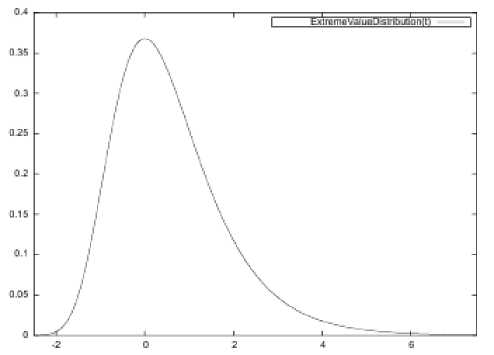
Figure. 1. An extreme value distribution when a = 0, b =1.

• III.    maximum of X with Poisson distribution

If maximum is taken using variables with Poisson distribution, we must take into account discrete character of the last. However, we can obtain expressions for average and standard maximum deviation, if we bring closer Poisson distribution by continuous function. We can obtain the expression for function f ( x ) and use it for search for values a and b . Then:

i - 1

Ф ( i ; 2 ) = ^ Poisson x ; 2 ) = 1 - ^ Poisson x ; 2 )     (4)

x = 0                      x > i

For i >>  λ , this expression permits close approximations [13,14] as:

; 2 ) -

Ф ( i ; 2 ) - 1 -1 1 - — | ■ Poisson i

I i )

_-3 2 ⁱ

- Poisson( i , 2 ) = e —.

Then we use Stirling approximation for factorial [13, 14] and we will get the following expression for function f ( i ):

f ( i ) = 1ln(2 n ) + X + i In i - (1 + In X )i + 1ln( i ).        (6)

a s = д/ 2 ln(2) y - ln(2 n ) - 2 ln( a s )

which can be solved iteratively, not paying attention to the right member in the first iteration. The derivative f(x) is determined as:

If we abstract the fact that i must be integer calculate the parameter a by solving the equation: ln(2) y = ^ ln(2 n ) + X + i In i - (1 + In X )i + ^ ln( i ),

we

can

x + — x , and therefore,

or, that is equivalent to:

a 1

--- ~ -- a_s + 1 a s

ln(2) y - — l n(2 n i ) - X i =-------------------

ln | i I- 1 V X J

,

which may be solved iteratively. Derivative f ( i ) termined by:

is

de-

i I i 1        1

ln l — I +— .

V X J  2 i

Roughly, maximum has distribution with average value

1,17 y and standard deviation 1,11 / y . Now we can find values a and b for any normal distribution with average μ(X) and standard deviation σ changing for х on X - A ( X )

°     . It gives:

a = σas+ μ(X),                                 (17)

Denoting solution a and using condition a >>  λ , we get:

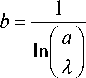
It follows, that if a is much more than λ , standard deviation becomes less than 1.

As maximum distribution is discrete, the small value of standard deviation results in distribution concentrating in two integers close to a .

• II.II.    Maximum of X with normal distribution

Now consider a particular case for variable x with standard normal distribution. Following [12], In this case

D ( x ) « [” Z ( u ) du J -от

For large values x, this integral law will be close to [2,3]:

1                          1        --X"

D ( x ) «1 -¹ Z ( x ) «1-- e ^{2 x}        xy 2 n

Thus we can get the following expression for the function ^{f ( x )} :

f ( x ) = - ln | — Z ( x ) | = — (ln ( 2 n ) + x ² ) + ln( x )

v ^{x      J 2}                           (13)

Parameter ^{a s} (subscript s for standard) is the solution of the equation:

b = σbs.

The above theoretical results are the ones that we will be guided by the experiments.

• III.    THEORETICAL AND EXPERIMENT EVALUATION OF MAXIMUM DISTRIBUTION OF FULL DIFFERENTIALS OF CIPHERS MINI VERSIONS.

Let’s give theoretical evaluation of maximum values of total differentials of mini cipher with 16-bit input and 16-bit master key.

As shown in [15,16], the laws of distribution of transitions XOR cipher tables mini asymptotically repeat a law conversion XOR distribution table of random permutations, which just obeys Poisson law [16]. Even at the level presented in [2-10] experiments performed to a limited set of encryption keys, it is seen that the results are practically independent of the use-played keys (for different keys, we have one and the same distribution of transitions, and the keys only affect distribution of one and the same set of transitions within the differential table of ciphers).

In our case power of the set of random variables is equal to the number of differential table cells without null string and zero column i.e. (2 ⁿ - 1)² for substitution of power 2 ¹⁶ we obtain y « 2 n = 32.

The equation (8) has the following form:

i =

ln(2) ■ 32 - 1ln(2 n ) - 1

Table I gives this equation solution by method of sort- ing.

Thus, equation solution (18) is a = 10. And then b =

ln ( 20 )

= 0,33 . Note that formula (8) by which we determined the value a, works with the transition half value of differential table. Therefore calculating average value we must double the result obtained. And then ц (X) = 2-10 + 2-0,4-0,58 = 20,386.

Table I. Equation solution (18) by method of

SORTING

i	ln(2) - 32 - |ln(2 ^ ) - 1
	ln ( 2 г ) - 1
8	11,71
9	10,40
10	9,84
11	9,36

This value agrees well with the results of calculations and experiments are presented in [4, etc.].

We have already noted that, since the distribution of the maximum of the discrete, the low value of the standard deviation b = —1^ = 0,333 leads to the fact that the ln ( 20 )

distribution is concentrated in two integer values near ц(Х) ® 2 a . In our experiments with small ciphers are two values: 18 and 20.

However, the formation of an integral of the distribution of the maxima of a random permutation of the differential table (3) we find that the expectation value 20 does not suit us, because in this case the number of peaks excluded is 18 (the probability of such values obtained almost zero, while the experiments show that this value is one of the most likely). Therefore, further calculations will be carried out for the value of a = 9 (this correction is permissible under and simplifications used to rounding.) In this case b = —1^ = 0,346. Then ln(18)    ’ ц (X) = 2-9 + 2-0,346-0,58 = 18,4.

As a result, we will use the final expression for the integral of the distribution of the maxima (3) as:

9 - X

0,346

Dmax(X) - e-e or

18 - 2 - X

D max ( X ) - e - -

0,692

The results of calculations by formula (19) is in good agreement with experimental results for random permutations, presented in our paper [4].

Table. II shows the results of calculations of the value distribution of maxima (for the whole set of keys), made in accordance with the expression (19).

Table II. Maximum Value Distribution Of Mini Cipher For The Whole Set 216 Keys Calculated By The Expression (19)

k * ( X 1 , X 2 )	Pr( k *)	Число значений	Экспер имент
18 (18,16)	0,366 - 1,2 - 10 - 8 = 0,368	24109	27724
20 (10,9)	0,9459 - 0,368 = = 0,5779	37876	28287
22 (22,20)	0,99691 - 0,9459 = = 0,051	3343	1912
24 (24, 22)	0,99982 - 0,99691 = = 0,0029	191	90
26 (26,24)	0,999990 - 0,99982 = 0,00016	10	2
28 (28,26)	0,9999995 -- 0,999990 = 8,5 - 10 - 6	0,5	0

In the right column of the table 2 the results for reduced model of Byelorussian cipher, obtained from the experiments, are presented. From presented results it follows that maximum maximorum value for reduced cipher models equals 26. This value, practically, doesn’t differ from average maximum of differential substitution tables. Thereby we confirm the statement (proposed in [3] and other papers) that evaluation cipher provable resistance can be made on the basis of maximum value of differential and linear probabilities obtained for one (any) cipher key.

The results obtained testify about rather good coincidence of theoretical and experimental results. Note that similar results were obtained by us and for other reduced cipher models (Kalina, Mukhomor, Rijndael and others).

• IV.    THEORETICAL AND EXPERIMENTAL

EVOLUTION OF DISTRIBUTION OF DEVIATION OF MAXIMUMS OF LINEAR CORPS OF CIPHER MINI VERSIONS

Consider then what we get for distribution of deviation maximums reduced to 16-bit size of cipher model inputs.

In this case we will take as the basis approximation of the law of random substitution deviation (cipher) as a normal law, proposed in the paper [12].

According to the results of our work the theorem is true (with some our changes in designations):

Theorem. For random n-bit substitution with n >  5 disbalance Imv( v.u ) is the random value with distribution, which can be approximated in the form of normal law

I                                         1

^Pr(Imb( V , u ) = ² x ) = Z          I .

I ( n 4) / 2 1

In our case disbalance is the bias of linear approximation table.

Using (14), for substitution of power ² we will obtain (in this case a set of random variables (2 16 - 1)² » 2 32 , i.e. again y = 32):

a s = J 2ln(2) y - ln(2n ) - 2ln( a s ) = = ^ 4ln(2) n - ln(2 n ) - 2ln( a s );

a s = ^ ln(2)64 - ln(2 n ) - 2ln( a s )

a   11

b s =      ” — = 7 = ^0,16

a_s + 1    a s ⁶

Table III presents the results of equation solutions (21) by the selection method

810 - X

20,2

D max ( X ) ” e ^- e . (24)

Table IV presents the results of calculations by defining distribution maximum values of linear hulls on the basis of the integral probability distribution law (24).

The presented results show that in this case the experimental data are close to the data calculated theoretically. Again, we can conclude that, in determining performance demonstrable resistance is possible to do a lin ear probability values obtained for the individual (any) key encryption.

Note that the results of previously performed theoretical and experimental evaluation of the values of the maximum biases of the linear approximation table random permutation of degree 216 equal to 748 (estimated) and 720 (experiment) [18].

We see that in this case is almost the same as the results of experiments results. We now estimate the maximum values of the full differentials and linear hulls for 128-bit encryption

Table III. Equation Solutions (21) By The Selection

a s	ln(2)64 - ln(2 n ) - 2ln( as )
7	6,21  0,79
6,5	6,23 0,27
6,4	6,22 0,17
6,3	6,19  0,103
6,2	6,234  0,0349
6	6,24  0,24

In this case we need to do a small correction will result, focusing on the experimental data. We will consider the value as = 6.33, respectively, and bs

^as      ¹

a s + 1   a s

— = 0,1579 6,33

(here we are already accounted for the results of this experiment, presented in Table. IV). Then, to have a degree

16 - 4

216 of substitution and a = 2 2  = 26 in accordance with (17) we have b = 64-0,1579 = 10, 11, and we arrive at the integral distribution law highs full differentials reduced 16-bit cipher model in the form:

405 - X

10,1

Dmax(X) ” e-- or for actual results doubling table biases linear approximations

Table IV. Results Of Value Calculations Of The Probability Distribution Law (24) By Method Of Sorting

k* (X1, X2) Pr(k*) Число значений Эксперимент < 768 3,02⋅10-4 20 27 770 (770,768) 6,5 10-4- 3,02⋅10-4= 3,48 10-4 23 21 772 (772,770) 13⋅10-4 - 6,5 10-4 = 6,5 10-4 42 44 774 (774,772) 0,00244-0,0013 = 0,0011 72 67 776 (776,774) 0,00431- 0,00244 = 0,00189 124 143 778 (778,776) 0,0072 - 0,0043 = 0,0254 190 149 796 (7…96,794) 0,1334 - 0,108 = 0,01 16…64 1696 800 (800,798) 0,1918 - 0,1614 = 0,03 1991 2033 808 (8…08,806) 0,3298 - 0,2937 = 0,036 23…67 2382 810 (810,808) 0,368 - 0,3298 = 0,0382 2503 2476 812 (812,810) 0,4028 - 0,368 = 0,0348 2280 2354 814 (814,812) 0,4390 - 0,4028 = 0,0362 2374 2399 816 (816,814) 0,4746 - 0,4390 = 0,0356 2333 2467 818 (818,816) 0,5093- 0,4746 = 0,0346 2273 2359 820 (820,818) 0,5428 - 0,5093 = 0,3358 2200 2320 822 (822,820) 0,5752 - 0,5428 = 0,0324 2123 2243 840 (8…40,838) 0,7977 - 0,7791 = 0,0186 12…19 1259 880 (8…80,878) 0,96954 - 0,9664 = 0,0031 2…05 186 900 (9…00,898) 0,9886 - 0,98744 = 0,0011 7…6 57 948 (9…48,946) 0,9989 - 0,99884 = 0,0001 …7 4 950 (950,948) 0,9990 - 0,9989 = 1,4⋅10-4 9 6 978 (9…78,976) 0,99976 - 0,99973 = 2⋅10-5 …1 1 1008 (10…08,1006) 0,999946- 0,999941= 5⋅10-6 0,…327 …1 ear probability values obtained for the individual (any) key encryption.

Note that the results of previously performed theoretical and experimental evaluation of the values of the maximum biases of the linear approximation table random permutation of degree 216 equal to 748 (estimated) and 720 (experiment) [18].

We see that in this case is almost the same as the results of experiments results. We now estimate the maximum values of the full differentials and linear hulls for 128-bit encryption

• V.    DISTRIBUTION OF THE MAXIMUM DIFFERENTIAL AND BIAS FOR THE 128-BIT ENCRYPTION

Here we can only make a theoretical estimate of the expected results.

By analogy with the above we present first the solution of (18) by linear search.

Table V. Equation solutions (18) by the selection

i	ln(2) ⋅ 256 - 1 ln(2 π i ) - 1 ln ( 2 i ) - 1
50	48
49	49,10
48	49,38
45	50,29

From Table V that as a solution, you can take i = 49. Then b = —Ц = 0,218, ln(98)

ц ( X) = 2 - 49+ 2 - 0,218 - 0,58 = 98,25.

As a result,

98 - 2 X

D max ( X ) - e - e

0,436

Examples of calculations based on this formula illustrated in Table. VI.

Table VI. Examples of calculations using formula (25)

2 i	98 - 2 X 0,436 e e
96	2,0358286656593905558806406692728e-44
98	0,368
100	0,99002431286177632139071000379891
102	0,99999900086153329513922193659255
104	0,99989991931925979806872668834032
106	0,99999999002576016001516033817533
108	0,99999999990042880442678108846006
126	0,99999999999999999999999999990196

The presented results show that in this case, would be the most severe (more likely) the two values of the maxima: 98 and 100. The remaining value of the maximum, which in this case is a representative set to be significantly less likely.

Based on the fact that the total number of cells in a differential table for 128-bit encryption (2¹²⁸ - 1)² = = 1,1579208923731619542357098500869e+77, we can conclude that the expected value of the largest maximum will be close to 192.

In assessing the strength of ciphers to differential cryptanalysis attacks can focus on the maximum value obtained for a chance to take a key encryption, which leads to the resulting probability.

98 : 100 _{= 2}-121

For the linear approximation table 128-bit encryption, we have (see Table VII):

Table VII. Solution of (21) in the manner of selection for 128-bit

as	V 2 - ln(2) - 256 - ln(2 ^ ) - 2 ln( a s )
17	18,638 (1,638)
18	18,635 (0,635)
19	18,6323 (0,367)
20	18,62 (1,38)

And, therefore, as = 19. Then bs

^as      ¹

a s + 1   a s

— = 0,0526, 19

as for 128-bit encryption о = 2(n 4)/2 = 262, arrive at the result a = 19-262 = 24,25-262 =266= 87747997204358712186.

We have a value close to the calculated for a random permutation of degree in 2128. [19] And further b = obs = 262- 0,0526 = 257.

This leads to the conclusion that the value of the max- imum displacement will be concentrated around the value of 262, and the maximum linear probability come to value

' 2⁶⁶ V

₇ 128 - 1

V ²      7

= 2 122 , which is consistent with previous results [19].

• VI.    CONCLUSION.

As the result of theoretical and experimental research made, the laws of maximum distributions (extreme distributions) XOR tables and bias tables of linear approximation transitions are established. In accordance with the results obtained for small cipher models we have come to the conclusion that practically all modern ciphers have rather small range of maximum changes of total differential and maximums of linear corps deviations so that it’s possible to use the results of maximum differential probabilities and maximum linear probabilities calculated for arbitrarily taken (one) cipher key for evaluation of provable resistance indexes of these ciphers. It is confirmed experimentally that cryptographic transformations inherent SPN cipher designs (ciphers with square S-blocks), are balanced in the sense that the quality of transformations made by them practically doesn’t depend on encryption keys.

For cipher as well as for random substitution of maximum differential values and linear halls maximums are not unexpected values. They obey to the integral law of distribution of extreme values of a set of independent random variables x , having one and the same distribution.