On the calculation of a model of a three-dimensional turbulent diffusion plume

DOI:

To describe the combustion process, various models are adopted based on the law of acting masses. One of the simplest and most widespread models is diffusion combustion. The most general analysis of the combustion of undisplaced gases was performed by Ya. B. Zel'dovich [1] and showed that during the combustion of unmixed gases, the flame front is

established at those points where the reactant flows approaching the front are in a stoichiometric ratio. One of the first serious attempts to construct a theory of a turbulent diffusion plume belongs to V.A. Shvab [2]. To simplify the calculation, V.A. Shvab proceeds from the assumption of the similarity of the fields of velocity, concentration and temperature in the plume [3,4].

A more detailed review of combustion studies can be found in [5] and others.

Numerous studies have dealt mainly with the combustion of unmixed gases in twodimensional plane and axisymmetric turbulent jets. In [5], taking into account that the aerodynamics of the flame and its stability are largely determined by the flow structure in the non -self-similar region - the zone of formation and stabilization of the flame, the method of the equivalent problem of the theory of heat conduction is used to describe three-dimensional flames. Within the framework of the method of the equivalent problem of the theory of heat conduction for calculating the distribution of velocity, temperature and concentration, as well as for calculating by stoichiometric ratios, the length of the flame is determined, where expressions for engineering calculations of a turbulent diffusion flame flowing out of a rectangular nozzle are derived. A detailed numerical study of the parameters of a flame flowing from a nozzle of a rectangular or any complex shape is practically absent in publications, but there are some works devoted to spatial combustion [6-8].

Taking into account the wide application of the problem of jet flow dynamics, it is of great interest to study propagating reacting jets flowing out of a rectangular nozzle with a finite aspect ratio.

Such tasks are used in the creation of various furnace devices, combustion chambers, efficient fuel combustion, etc. However, it should be noted that the main experimental and few numerical studies are devoted to the study of air outflows [9,10] as well as chemical reactions [11-14].

PROBLEM STATEMENT

In this paper, a three-dimensional model of diffusion combustion is presented in the case of a combustible gas mixture flowing out of a rectangular nozzle and propagating in a flooded (with a passing) air flow (figure 1). To describe the flow, we use three-dimensional systems of Navier-Stokes equations for multicomponent chemical reacting gas mixtures [15], which has the form

Mixture equation for gases:

∂ρu  ∂ρv ∂ρw дx    ду дz ’

The equation of motion along the x coordinate:

∂u     ∂u     ∂u   ∂P  ∂    ∂u   ∂∂ pu   + pO'  + pw   =-   +  (ш ) +

TT

∂x     ∂y     ∂z    ∂x  ∂y    ∂y   ∂z

The equation of motion along the y coordinate:

du     dv     ди    дP  4 д , ди д ,   дv_x  2 д ,   дw₄  д ,   дw₄

pu   + pu-   + pw =-   +     (ш ) +    (ш ) -     (ш ) +    (ш ),

TT TT дx     ду     дz    ду  3 ду    ду   дz   дz   3 ду    дz   дz    ду

The equation of motion along the z coordinate:

дw     д w     dw дP 4 д Ow д . Qw. д . ди 2 д . до

Р^и_? ^{+ pu}PT ^{+ pw}PT = -РГ + Ч ~^^^Pt 1Г)⁺ "-Р^(рт РГ) ⁺ 1Г( ^рт "дГ^-^ ~^^^Pt ir), дx     ду      дz дz 3 дz дz ду ду ду дz 3 дz ду

Energy transfer equation (total enthalpy):

дH     дH      дH    1 д ,   дНх   1 д ,   дHx  ,,   1 ,гд , дих pu--+ pu--+ pw---=--(ш---) +      (ш---) + (1--)1   (ши ) +

TT   T дx      ду       дz   Prr ду    ду   Prr дz    дz       Prr  ду     ду

д , ди.    д . дv.    д .     д w     4    1     д . дv.    д .     дw._n

⁺ — ( Шт^и "^) ^{+   (} Шт ^и ^) ⁺ 7“ ⁽ ^ t ^w ^)]⁺ (т ^-   )Ь- ( Шт° ^) ^{+   (} ^ t ^w -т-)]

д z      д z    д z      д z    д у      д у    3  Pr_r   д у      д у    д z      д z

-

-

д ,2 dw, д , дw. д , до д ,2 дv. — (- Шт ^и "^)⁺ ( Дт ^и ^) ⁺ т- ( ^ t ^w ^)^- — (- ^ t ^w ^) д у 3 д z д z д у д у д z д z 3 д у

Total enthalpy:

и2 + и2 + w2  ^4*

H=c T++ pii

.

The equation of state of the gas mixture:

N k

P =ρ TR ∑ ^Ci i = 1 m_t

For the three-dimensional case, the equation for the concentration of the i- th component has the form:

Р^^ + р^у^ + Р^ш^ = ^(^^) + т-у(^^) + <^^1 .        (1)

ox      ду      dz   ScT\ ду)  ScTdz\ dz)

Here x,y,z are Cartesian coordinates; u, u, ware the velocity components along the axis, respectively x, y,z; p - density; C i - mass concentration of i -th component; Sc_T - turbulent Schmidt number; p - turbulent viscosity; w i - mass formation rate i -th component.

SOLUTION METHOD

Let us describe the method of transformation of the three-dimensional equation of the concentration of the i -th component leading to one equation for a four-component mixture of gases during diffusion combustion.

It is assumed that the reaction proceeds in the zone of contact between the fuel and the oxidizer. Usually this zone, which is an infinitely thin surface, is called the flame front. On the surface of the flame front, the flows of the oxidizer and fuel must satisfy the condition of stoichiometric equality of the consumable and formed substances wfV3m3 + a)3Vtmt = 0,                              (2)

those. the concentration of the oxidizer and fuel at the flame front are equal

(C i ) ф = (C₂) ф = 0.                                (3)

Equation (1) for problems (models) of diffusion combustion can be reduced to a more compact form pu^ + pu^ + pw^ = ox 1 oy        oz

—Of oSA

Sc_T dy ^p dy

” ТГ ^Р -Г ¹ ) + w i • |v₃ m₃

Sc_T dz К dz /        t I 3    3

.

pu^ + pu^ 3 + pw^ 3 = ox       oy       oz

"~T"(p °r 3 ) +~т(р °г 3 ) + w з • Ivm

ScT dy    dy     ScT dz    dz        3    1  1

Adding (4) and (5), we get

d

d

d

p^U "dx ^{(C i V} 3 m 3 + ^C 3 ^v t md +p^v^ ^(c i ^v 3 m 3 + С з^ ут) + pw — (Cf^m ^ + С з ^т )

1 o     o                                1 o     o

= i^ r sy [ ^p oy ^(c i ^v 3 ^m 3 ^{+ C} 3 ^v i ^m i )J+ s; ; 5; [ ^p 5; ^(c i ^v 3 ^m 3 ^{+ C} 3 V i ^m i )J.

Here the condition of stoichiometric equality of the amount of consumed and formed substances is used (2), or where,

act,    ac^

^pu a " + P^uv^p™

ac t i a

T"=~ az  scT ay

i a scT az

(pS ,

C = C i - g i g + Г з -^.                        (8)

Using the conservative Schwab-Zel'dovich function with respect to excess concentrations

~ ~

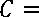
. ^c" ^¹ , i = 1 - 3

(C t ) 2 -(C t ) 1

does not change the form of equation (7)

ac ax

~           ~            ~

ac ay

ac az

i a s c _T ay

Ip~) +

i a scT az

(-a

The function C takes the value 1 in the fuel nozzle exit, and 0 in the air zone (here the second indices indicate that this value belongs to the air-1 or bitter-2 nozzle exit). The introduction of function (9) makes it possible to get rid of the source a term in the diffusion equation (1) and reduces the number of diffusion equations to one for a four-component mixture (10).

At a finite reaction rate, it is necessary to integrate the diffusion equation for each component separately.

Using condition (3), from relation (8) we find

(^(С 1 ) ф = ^(С 3 ) ф ^- 1 ^т 1 , l ^(С 2 ) ф = ^(С 3 ) ф’ ^и 2 ^т 2 .

Using (11), from (9) we determine the value Cat the flame front (see Fig. 1, which shows the spatial shape of the flame), i.e. Сф

^Ci ) 1 ⁽ 1 ^-С ф )= 1 2 ^ 2. ^(С ф ) ⁽ С₂ ⁾

or

(C i ) 1 -17111

^(C i ) i - 17 1 1

+

^(C 2 ) 2

- 2 1 2

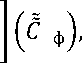
1 from here               ^ = „ц*^ v2m2(c1) 1

(12)

From (8), (9) we find the distribution of the relative excess concentration of fuel, oxidizer, inert gas reaction product using the following boundary conditions:

Г (С 1 ) 1 — (C 1 ) 1v3 m 3 ,     (С 1 ) 2=0 , t(С 2 ) 1 — 0, (С 2 ) 2 — (C 2 ) 2 V 3 m 3 .

(13)

The condition C > C ф corresponds to the fuel region, 0 < L(y,z) < Л ф (у,х), the concentrations of the components are defined as

^C 1 — 0  ,

jc2—с [ (C2) 2+;x (Ci) i]   :i:i (m 1, рз   'f  Ьф(у,2)],

^C 2 = ⁰ ,

C i — [ (C i ) 1 + :^ (C 2 ) 2 ](^ , Л        L             И 2 Ш 2          J > C     : : : : (« 2 c    .

(15)

For an inert gas N 2 , its distribution relative to the excess concentration and the boundary conditions will be the same as for C , therefore

c^-tzy 1  _ - (C-d 2-(C4) 1 (16) C4 — (C4) 1 + [(C4) 1 — (C4) 2] C, (17) where expressions (17) are valid in the entire investigated area of heat and mass transfer. Formulas (14 - 17) when calculating C make it possible to unambiguously find the values of the concentration of all components of the flow region. The reliability of determining the concentration of the components can be checked using the identity

E^i Q — 1. (N_k —number of components).

As an example, the combustion of a mixture of propane a - butane in air with different values of the jet parameters was studied. The reaction proceeds according to the stoichiometric equations:

I C 3 H 8 + 50 2 ^ 300 2 + 4H 2 0 +            kkal/gmol

[c4H10 + 6,502 ^ 4C02 + 5H20 +         kkal/gmol

• ^v 0₂ ^— 5,75; ^v C 3 H 8 +C₄H₁₀ ^{— 1 V} C0₂ ^— 3.5 ; ^V H₂0 ^— 4,5;

• ^m 0₂ — ³² ; ^m C₃H 8 +C₄H₁₀ — 41; ^m C0 2 — ⁴⁴ ; ^m H 2 0 — 18; ^m N 2 ^{— 28} , because 0.5( C 3 H 8 + C₄H₁₀ ), the mol is 1 mol of the combustible mixture, which we denote by A and the unified stoichiometric equation can be represented as

  A + 5.750 2 ^ 8D + ^^ .                    (19)

The parameters of fuel A and the combustion product required for calculation D — 7СО2^н 2 о (he_at capacity, molecular weight, thermal conductivity) are determined according to the laws of thermodynamics.

So, from the point of view of mathematical calculation, we consider a four-component mixture of gases in the mixing zone, consisting of oxygen O 2 - index “1”, a mixture of propane a - butane (C 3 H 8 + C₄H₁₀) — "2", combustion products C0 2 + 9H 2 0 — "3", inert gas N 2 — "4". From a physical point of view, 6 components are involved in the zone of heat and mass exchange.

NUMERICAL RESULTS

We present some numerical results, as in the line of the initial value of the speed of the hot mixture on the parameters of the torch.

For the numerical solution describing the flows, an efficient method [12] similar to SIMPLE [15] was used, that the corrections to the velocity are determined by the corrections to the pressure in accordance with the approximate equations of motion, in which the longitudinal convective terms are balanced by the pressure terms.

To calculate the turbulent viscosity, a semi-empirical formula was used that takes into account molecular transfer, three-dimensionality, and temperature inhomogeneity of the jet in the form [13].

p = xpi ² (y.z)j(% ) ² + (^) + (^) ф«.

In this case, the combustion of a propane-butane mixture flowing from a square-shaped nozzle and propagating in a concurrent oxidizer flow was calculated [4] under the condition:

• I.    Oxidizer zone:

T 1 = 300 K; u 1 = 0; (C 1 ) 1 = 0,232, (C₂) 1 = 0; (C₃) 1 = 0; (C₄) 1 = 0,768.

• II.    Fuel zone:

T₂ = 1200 K; u₂ = 61 м/с (18,3 ; 30; 38 m/s);

(C i ) 2 = 0; (C 2 ) 2 = 0,12; (C 3 ) 2 = 0; (C 4 ) 2 = 0,88 ;

Рг_Т = Sc_T = 0,65, p 1 = p₂ = 1 atm.

Figure 2 shows the shape of the torch depending on the initial value of the velocity, while other parameters of the jet and the oxidizer remained unchanged. As can be seen from the graph, when the speed changes u2 from 18.3 to 30 m/s, the linear dimensions of the torch increase with increasingly up to 61 m/s, they practically do not change, even at u2= 70 m/s.

Figure 3 shows the change in the concentration of the fuel and the C2 reaction C3 product along the axis of the submerged diffusion flame at fuel velocities iy=18.3 m/s (---) and 61

m/s (        ) .

The change in the axial concentration indicates that, as one moves away from the nozzle exit, its value decreases atiy = 18,3m/s faster than compared to iy = 61m/s.

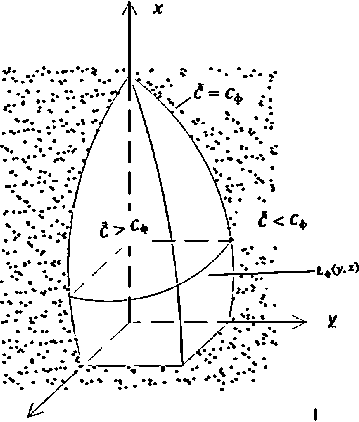
z

• Figure1. Spatial shape of the torch.

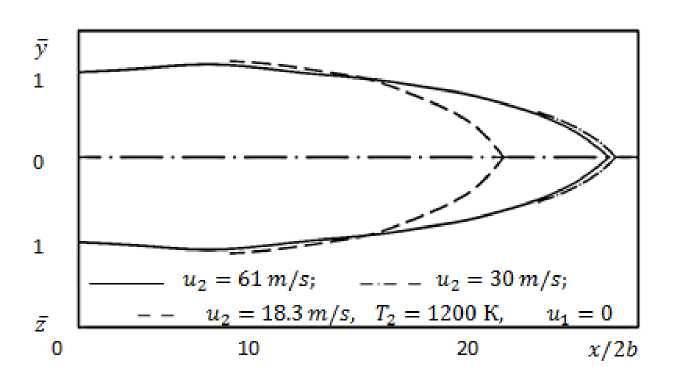
Figure 2. Torch configuration at various initial jet velocities.

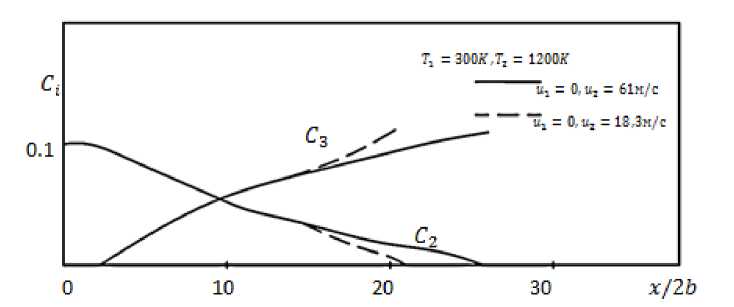
Figure 3. Changes in the concentration of the fuel С₂and the reaction product С₃along the axis of the flooded diffusion flame.

CONCLUSIONS

At jet velocities of 18, 30, 38, and 61 m/s, respectively, the maximum temperature reaches 1943, 1845, 1850, and 1909 K.

The results obtained will help in the selection of the initial jet velocity, to obtain the required length and temperature of the flame during diffusion combustion.