On the choice of orbits for spacecrafts

The studies which begun in [1] and were devoted to solving the problem of choosing the most favorable orbits for spacecraft of one class or another, as well as the problem of distributing a given number of satellites over a given set of orbits with existing prohibitions on satellite detection in some orbits, are continued. The article provides a solution to this problem under the following conditions: the number of satellites n coincides with the number of possible orbits where satellites can be located; each satellite is forbidden to be in exactly one orbit; two satellites cannot be in the same orbit; the number of orbits is broken into non-overlapping blocks of a certain configuration ( n = p k ). A formula is given that allows to calculate the number of possible combinations for the satellites distributions over such orbits.

Problem statement, definitions, labeling

Mathematical model of the problem. By permutation we mean a one-to-one mapping written in the form of a table of dimensions 2 x n :

( 1   2   . n

^g = ; у         ;

V i 1     i 2    • -- i n

A permutation is called regular if k ^ i_k , i. e.

i 1 ^ 1, i 2 ^ ², • • •, i n ^ n .

It is worth reminding that the order of permutation in the group-theoretic sense is understood as the minimum possible natural number m , where

g

m

( 1  2  . n Л ( 1  2  . n ^    ( 12  . n }

•                                   •••••

V i 1     i 2     • ••    i n J  V i 1     i 2     • • •    i n J       V i 1 i 2     • •• i n J

V 1

2 ...    n_y

m раз

– a single permutation. In this case, the product of permutations is a sequential execution of multiplier mappings. In this paper, we will consider the case n = p^k , where p is a prime number. We will consider the problem of listing all regular permutations of degree n that have order p . By the cyclic form of a permutation g , of degree n , and of order p , we mean the following:

( 1   2  •••

g =

I i 1    h •••

n in >

^'•Л11)-

p ") p

^L n - p +1 • • • nn

The above terms from the permutation theory can be found in [2]. Thus, each variant of the satellites position in orbits indicated above will correspond to exactly one regular permutation of the form (3). Additionally, an estimate of the complexity of calculating the number of indicated orbits is given.

Main results

The number of regular permutations of degree n = p^k and of the order p will be denoted by R ( n , p , k ) .

Theorem 1.

( P^k ) ^!

^{R (} n , P ’ ^{k ) =}    k - 1 . _klp                                   ⁽⁴⁾

P^p    • ( P^{k -} ' ) !

Proof. Number of possible combinations for the first cycle (i(1)...i(1)) equals pk • (pk -1) •. • (pk - p +1).

Taking into account the fact that the cycle does not change as a permutation during a “circular” shift of elements, we have:

p^k • ( p^{k - 1} ) '.' ( p^{k -} p ^{+ 1} )

p

The number of possible combinations for the second cycle ( i ^{( 2 )} ...i⁽_p 2 ) ) equals

( p^{k -} p ) • ( p^{k -} ( p + Of.' P p^{k -} ( ² p ^{- 1} ) ) .

Taking into account the fact that the cycle does not change as a permutation during a “circular” shift of elements, we have

( p^{k -} p ) • ( p^{k -} ( p + ! ) ) •.* ( p^{k -} ( ² p ^{- 1} ) )

p

Proceeding in a similar way for the last cycle with number ( p^{k 1} ) , we obtain

( p^{k -} ( p^{k -} p ) ) • ( p^{k -} ( p^{k -} ( p ^- ! ) ) ) •.• ( p^{k -} ( p k ^- ( p ^- ( p ^{- 1} ) ) ) )

p

( p^{k -} p ) • ( p^{k -} ( p ⁺ ! ) ) •.• ( p k ^- ( ² p ^{- 1} ) ) x -----------—------------------------------------------— •... x

p

• * P p J- P p 2 ^p )H p 2P ^p lzP ^p 2 ¹ ) )^ . P p zP p zP ^p z P ^p^ ^p

p^k !

p

( p^{k - 1} )

To complete the proof, it suffices to divide the specified value by pk 1!. We obtain pk!

.

k -1.

!

R ( n,p,k )=  / k-П pp ■ p‘

The theorem is proved.

Estimating the complexity of an optimal algorithm for computing the number R ( n , p , k )

Here are some useful properties of numbers R ( n , p , k ) , the second of which is of the greatest importance, where an estimate of the complexity of the optimal algorithm for calculating the number is given.

Definition. Suppose A(n), B(n) are numerical functions depending on the natural number n . The

An lim 4^ = 1. n ^® B ( n )

expression A ( n ) ~ B ( n ) means that

Theoreme 2. Under n ^^

R ( n , p , k )□ p ² ( p^k / e ) p  p^P

.

Proof. In view of the classical

asymptotic Stirling formula for the factorial n ! under n ^^ :

_k p ^k

R ( n , p , k ) =

_pk _!

p ⁽ p ^{k - 1)} ■ p

,^k - ¹!

p^k - ¹ p ^p

e

J 2n p^{k - 1} | p

k - 1 k -1V

e

p

■ 2 —

V ^e )

p^p -

p

k ^p

, k p

V ^e )

k

p

k    kp

² V

V ^e )

k

p

---( n k - ¹ Y k -1   P

. k - 1

£-1 k -1 ( к -1 \ p

k

p

V

/

e )

_kp ^k

2^

V ^e )

p ^k - ¹ p^pp

k ppk

( n k -1 Y

/'

V e )

. k - 1

= p ^{2 p}

p^p p ²

p

1 k

² V

V ^e )

V ^e )

k

k -1 /

p^{k - 1} 1

p ^{k - 1}

V e )

p

p

V

n k -¹ Y

2—

e )

. k - 1

p

1 ( n k -1 Y

■^{2 p}„

V ^e )

p ^k - ¹ p^p

k -1 \P

V e )

The theorem is proved.

k

^k p^p

( „ k -1 Y V e )

. k kk - 1

• P^pk

. k - 1

, k - 1

p ²

p^k - ¹ p ^p

= P

. k  kk - 1

p

e

2 p r

V ^e )

.

■ p p

Formula (5) shows that the number R ( n , p , k )   grows very fast with increasing k, as

O

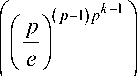
At the same time, V. V. Kochergin in 1994 in [3] presented an optimal algorithm

to find the value 2 ⁿ (based on 2) for

O ( log n )

arithmetic multiplication operations. In turn, R. V. Borwein in 1985 in [4] gave a fast algorithm for calculating the factorial n !, the complexity of which is equal to

O ( n ( log n ( log ( log n ) ) ) 2 )

(also refer to [5; 6]). Complexity estimates (6) and (7) as applied to formula (4) for the

number R ( n , p , k ) , containing two factorials ( p^k ) !and ( p k ¹ ) !, give the following result.

Theoreme 3. The fast Kochergin and Borwein algorithms for n = p^k and n = p k ¹ respectively generate an optimal algorithm for calculating the number R ( n , p , k ) , with complexity equal to

O ( p k • ( log p^k • log ( log p^k ) )

Generating functions of various types, as well as integral representations of functions of one and several complex variables, are the main tools of modern enumerative combinatorial analysis [7–15]. Using the following well-known integral formulas for the factorial n ! and 1/ n !, for example [6],

n ! = J s n e ^sds , 0

— =--- e x x 1 dx,  0 < у < да, n!    2n i. r

| x =Y

we obtain

Theoreme 4. The number R ( n , p , k ) has the following integral representation:

R ( n , p , k )

да                   1

= f sⁿe~ s ds--

^{J          2 n i}

J ^e x ^x

■ - n ^{- 1} dx ,

0 < у < да .

| x =Y

We will carry out the final calculations using the method of Egorychev coefficients of the integral representation and the calculation of combinatorial sums [14; 15].

Definition. Let us introduce into consideration integrals of the form да

H p ( 8 ) = J e - ^s ' s p ds ,                                       (12)

where p - prime number; 5 - real number, independent of s .

Supposing  S(z)  - generating function of power type for the sequence R (n, p, k), k = 1, 2, …, да                           дак

S ( z ) = Е R ( n , p , к ) z n = E R ( n , p , к ) z^P

.

к=1

Theorem 5 (integral representation for the function S(z)). The generating function S(z) admits the following representation:

1      _ да.

S ( z ) = — f f e ^{- + tz s} t ^{- 1} A ( t , к ) dsdt ,

where the function (series) A(t,k) – the kernel of the integral representation of the function S(z) has the following form:

да

A ( t , ^к ) = Е ( pt )

к =1

—

к - 1

, | pt | > 1 under any p

or taking into account (12)

S ( z ) = i f t ^-1 H p ( tz p ) A ( t , k ) dt .

Proof. Applying the formula (11) for the numbers R ( n , p , к ) , we have “     ,          . к

S (z ) = ЕR (n, p, к) zp = к=1

p ^k - ¹

p

p ^к - ¹ p^p

„да

Е -^p к =1

да / p ^k

e s ds •— [ e^xx ^{1 p} dx = 2n i । r

| x =Y

p ^k - ¹ p^p

да

е ( -^{рк - 1} ) ^p к =1'         '

»

¹ Г x - 1 - p ^{k -1} , --- I ex ^p dx =

2 n i , r

I x =Y

да

да

да да          „

ЕЩ z m ) p f ( s m )

к = 1

m = 0

I p e s ds •— j e x x ^{1 p} dx •§ ( m - p^{k 1} ) > .

² ”H =y                     J

Here б ( m - p^{k 1} ) - delta function:

8 ( m - p^{k 1} ) = — f e ^{1 + m p} dt ,  (0 <  u <да )..

2 n i J

Then, the formula (16) has the form

да

да

да

p ^к - ¹ p^p

ЕЩ - m ) Ч( s p )'

к =1

m =0

m                                       1 г         к - 1

I e ^- ds • — [ e x x ^{m - 1} dx • — f e^m-^p dt

2n i r              2 n iJ

(regrouping the terms in the last sum, highlighting in square brackets those that contain the index m )

да

да

да

p ^k - ¹ p^p

да 1         да да

Efe f f Е(t-psp) • к=1 [ 2Пi |t|=u 0 Lm=0

— f e x x’ m ^-1 dx 2n i । r

| x =Y                 .

• e s t ^{1 p} dsdt

(summation in square brackets at index m , substitution rule, permitution x = tz^ps^p )

p ^к - ¹ p^p

дат . да „  „

Е—; f f etz x e-t-1-p  dsdt = к=1 2ni |t|=u 0

(entering the summation sign for the integral sign). At the same time, since the choice of the parameter u is not limited by anything, we choose u > 1/2, so that the inequation \tt\ > 1 is satisfied for any prime p,

1      X

=

2 n iJ a

1 1 = u 0

e

,- s + tzPsP

( x

t -1 Z ( pt )

у k =1

.— p k ^-1

dsdt ,

which completes the proof of the theorem 5.

Conclusion

Thus, the problem of distributing satellites over a given set of orbits under certain conditions has been solved: the number of possible combinations is determined by the number of regular permitutions R ( n , p , k ) . An estimate of the complexity of the optimal algorithm for calculating this number is given.

It should be noted that transformation (16) is somewhat paradoxical, since it introduces an additional sum over the index m and therefore substantially complicates the original expression. However, this transformation together with the introduction of the delta function, made it possible to obtain an integral representation of a new type for the number R(n, p, k). We also note that it was the first time transformation (16) was encountered in practice of the coefficient method, which provides new opportunities for the above method effective application.

In view of the above it makes sense to pose the following problem: to study the properties of a

X

(new) special function H_p ( 8 ) = j e ^{- s +8} s P ds - part integral representation kernel (15) of the generating 0

function S ( z ).