On the determination of the main parameters of a dam compactor

This work is licensed under a Creative Commons Attribution-Non Commercial 4.0 International License (CC BY-NC 4.0).

Цитирование: Каримов М.С. К определению основных параметров дамбоуплотнителя / М.С. Каримов // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(5). С. 626-631. DOI: 10.17516/1999-494X-0251

It is known that for compaction of soils, compactors with sliding, rolling and vibrating working bodies are used.

The working process of each type of compacting devices consists in soil compaction without bulging it on the surface of the dam, that is, without their longitudinal and transverse movement [10, 11, 12].

As a result of patent and engineering studies, we determined and justified the parameters of a channel digger that provides the smallest dead depth and high dams. However, it turned out that in order to increase the water holding capacity of the dams of the temporary irrigation, they need to be compacted in order to reduce the amount of irrigation water for washing the dams of the irrigator [3].

Studies show that the shape of the cross section of the temporary sprinkler dam after the passage of the trencher is significantly different from the shape that is obtained at the time of its formation [1].

The poured soil, crumbling at an angle of repose, gives the cross-section of the dam a trapezoidal shape (Fig. 1).

Cutting of temporary sprinklers with a backhoe as well as parameters of the cutting depth of the soil should meet the requirement of predetermining the top width of the dam. Therefore, the above parameters cannot be arbitrary [1].

When determining the volume of soil displaced by the digger, the angle of rupture is equal to the angle of repose, i.e.:

ф^=ф„=ф.

Then, the displaced volume of soil can be determined by the cross-sectional area (S1) taken out by the channel digger [1,3].

S, = КН_Ь -hV ХН_Ь -h)- clgg) - 4hclg^Hb " A).                     (1)

Converting of the expression (1) will lead to the following form:

S, = ЬН_Ь -bh- 1H; -h) + 2lrag^ ,                                   (2)

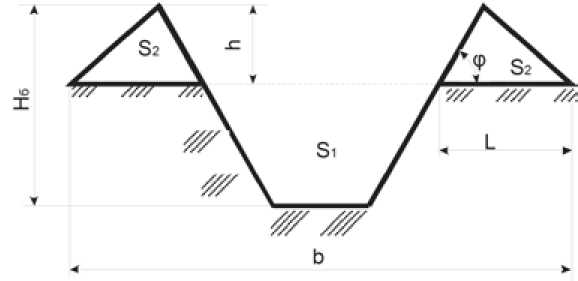
Fig. 1. Scheme of temporary irrigator dam where b – width of the occupied strip of the dam or of the temporary sprinkler; h – dam height, m; Hb – depth of temporary sprinkler, m; φ – angle of repose of the soil, deg.

The cross-sectional area (S2) of the volume of soil laid by the trencher in the crest of the dam can be determined from the expression:

S^l^lh-clg^ .                                        (3)

Since the coefficient of soil fluffiness when cutting temporary irrigators is equal to one [1,2], the volume of soil taken out by the channel digger will be equal to the volume of soil laid in the crest of the dam, i.e.:

S 1 = 2 S 2

Equating the expressions (2) and (3), we obtain the following equation:

bHh-bh — 2Hl = G

From equation (4) we determine the height of the crest of the temporary sprinkler dam:

НДЬ-2НД

Analysis of equation (4) shows that the height (H) of the dam depends on the depth ( Hb ) of the temporary sprinkler and the width (b) of the strip of the dam.

The width of the strip of the dam or the temporary sprinkler is equal:

b=H + 2(H_h-hyt^ ; b = В + 2H_hctgq> - 2h_xctg^ .                     (6)

The solution of equation (6) with respect to the width of the dam at the top will lead to the following form:

B = b-2clg^H_b-h^ .                                          (7)

The results of early studies of the shape of the formed dam when cutting temporary sprinklers and its compaction show the effectiveness of the conical shape of the roller [1].

During operation, the conical roller rotates on its axis with a sliding characteristic typical to passive compacting rollers, that is, having no rotating torque on the shaft. To find out the effect of sliding on the longitudinal displacement of compacted soil particles on the surface of the dam, we graphically consider the nature of the impact of the base of the conical part of the roller on them. Suppose that a conical roller moves with sliding (Fig. 2).

By decomposing the normal pressure force into the components Qm and Tm we can assume the following, if:

• 1.    Tm ≤ F 2 , then the surface particle under the force of Qm moves more along the dam rather than deep into it;

• 2.    Tm >  F 2 , the resultant of external forces Qm deviates from the normal pressure Nm at an angle φ₂ in the direction opposite to the rotation of the roller. In this case, the longitudinal movement mm ′ of surface soil particles will be greater than the movement into the depth Q ′ m ′ of the dam;

• 3.    It can be easily seen that the resultant of forces is determined from the expression:

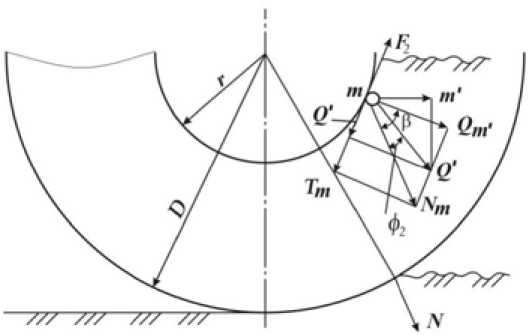
Fig. 2. On the substantiation of the dam compactor parameters

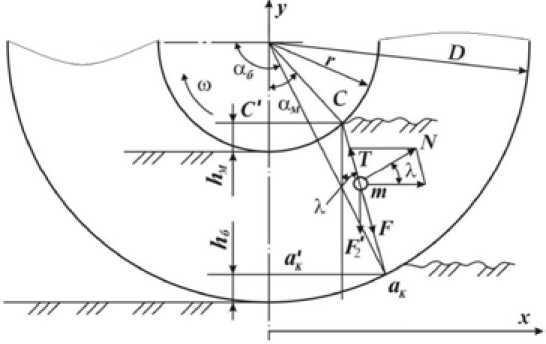
Fig. 3. On the determination of the angle of advance of soil compaction by conical roller on the slope of the dam

Q' =N„Xtg^-tg^ .                                           (8)

Whence it follows that the larger the angle β and the smaller φ 2, i.e. the smoother the roller surface, the less Qm deviates from N_m , and the greater is the immersion of the soil particles into the dam.

Consequently, the least compaction of the dam soil by sliding rollers is achieved at lower values of the angle of external friction of the soil.

For example, the conical part of the roller compacts the soil of the dam slopes with the depth of immersion of the large base and the small base (Fig. 3).

tg«.= ^l— ; 1" = а^ка'к-С\С; ,                                              (9)

where l ′′ – length of the opposite leg, m; l ′′ – length of the adjacent leg of the lead angle of compaction, m.

• I" = /)sina_f -rsin a,„; 1 = D-h_b- rsin a_m,

where D and r – the radii of the large and small bases of the truncated cone of rollers; α_b and α_m – angles of immersion in the soil, deg.

Substituting the values found in the above formula, we obtain:

. _ Dsina₆ -rsina,,, q>a —                   ,

αm, then:

D-hb -rcosam where hb – the depth of immersion of the large base, m.

h_b = D - Dcosa_b - R(\ - cosaj = 2Dsin—-.

Hence:

. Z) sin cl -rsina /gX =-------^---------= .

Deos a,, -rcosa,,,

If the angles of immersion of the large and small bases are the same, i.e. sin αb = tgλ = tgλ.                                                                           (13)

This means that the angle of advance of compaction is equal to the angle of immersion of the roller base. Therefore, according to equation (12), the greater the immersion angle of the conical base of the roller, the greater the angle of advance of compaction:

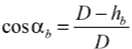
sma_b = ^h_b(2D-h_b') .                                         (15)

Similarly, we define:

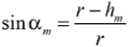
SIM О* _m     x]^m^^"^* ^m^ .                                                               (17)

Substituting the values of the values found in the formula (12) and after a series of transformations, we obtain:

^2R-h„Vh_m(2r-hJ D-r-h_b+h_m

From expression (18) it follows that with increasing immersion depth ( h_m ) of the roller small base, the angle of advance of the compaction decreases, and with increasing immersion depth (h) of the roller large base – it increases. With an increase in the radius (r) of the small base, the angle of advance of the compaction decreases, while with an increase in the radius (D) of the large base, it increases. If the immersion depth of both bases of the roller is the same, i.e. h_b = h_m = h , then formula (18) takes the form:

V* (2D-A)-(2r-AJ

^= -----7;-------

D-r

So the greater the difference between the radii of the greater and lesser bases of the roller, the greater the angle of advance of the compaction.

Assuming that the roller stands still, i.e. ν = 0 and Q = 0 , and using the limiting values of the angle λ , which will be equal to the angle φ 2 at which the subsidence of the soil particles of the dam is completely eliminated, then in equality (19) it is possible to establish the relationship of radii D and r :

л = Wicosc^-sina^ /^Ф2 cosaA -sina6

The relationship between the angle of advance of the compaction and the diameter of the conical roller is established. Analytical dependences for determination of large and small diameter of a conic roller are deduced.

Studies have established that in order to obtain the greatest effect of dam compaction, the main parameters of the dam packer should be as follows: a large diameter of the cone roller 540 mm, ski length 643 mm, ski width 360 mm and the angle of the dam 30°.