On the function of time distribution of a complex computing system uptime

Introduction. Any space computing complex is a complicated system. A complicated system is understood as a set of functionally related heterogeneous devices designed to perform certain functions and solve problems facing the system. One of the important characteristics of a system is its uptime. This characteristic is often considered to be a random variable. However, such a mathematical model is quite limited, since the uptime depends on many characteristics (parameters) that describe a system.

Therefore, the uptime can be assumed to be a continuous random function of many variables. Such an assumption is used in the literature [1–15]. In this work we will also stick to it.

It is known that the characteristic functional of a random variable Y in the Hilbert space H is the functional

Ф y (Z) = E exp{i (Z, X)}, where z e H, (Z, Y) is the scalar product in H, i= -1,, Е is the sign of mathematical expectation. Let R be the covariant vector of a random variable Н, EY = A. If Y is a Gaussian vector in H, then its characteristic functional has the form:

Ф Y ( Z ) = exp{ i ( A , Z ) - 2( RZ , XZ }.

The converse is also true, that is, if Y has a characteristic functional that meets these requirements, then its distribution is Gaussian.

The covariant operator R of the Gaussian vector Y is a kernel and completely continuous one; therefore it has an orthonormal basis of eigenvectors e k , k = 1,2,… Let us denote X _k , that is, the eigenvalue of the operator R , corresponding to the eigenvector e k . Let X _k > 0 be random variables

( Y — A , e k )

Ьл=

N X k which are independent, have a normal distribution and Eek = 0 , Eek = 1. Thus, the Gaussian vector Y can be written as да _____________

Y = A +ZVX ke kek.

k =1

The representation of the Gaussian vector Y can be used in various calculations. In particular, if we denote ak = (A, ek), then the characteristic function for the real s of a random variable Y 2H has the form exp«

да ф л( 5) = E exp{ IS^H №

¹ Yh                   ^V ’ k =1

2 X k a k S

1 - - 2 si X k

J 1 - 2 si X k

It is known that the distribution F ( x ) of a random variable is uniquely restored by the form of the characteristic function ф ( t ):

1 ^+да »- itx - ity ^y

F ( y ) - F ( x ) = — J-----_:----- ф ( t ) dt ,

2 n it

-да then да 1

^Ф| y ^^{( S} ) = П 8 ... .

^{1 1} h k =1 V^{1 - 2} is ^X k

Statement of the main results.

Theorem 1. Let Xk be the eigenvalue of the covariant operator R of a Gaussian vector Y. Then the probability of Y falling into a sphere of radius r is э +да 1             i да

p(|YH < r) = - J -exp j -- £ In(1 + (2tXK )2 ) > n 0 t I 4 k 2 =1

X

tr ² + £ arctg2 1 X _k + 2 n k     2

tr x cos---------------------sin— dt .

Theorem 2. Let X be the maximum eigenvalue of the covariant operator R of a Gaussian vector Y . Then the probability of Y falling into a sphere of radius r is equal to:

Substituting the introduced notation in the formula, we obtain

2n 2 ^{r 2 H} ”ⁿ ! 1 4 1 + (2 1 X )²

tr ² sin dt .

1 да -

P (I Y H ⁵ r 2 ) = 2 ; /-

-да

-1 £ ln(1+(2 1 X _k )²) , 4 k = 1

t

The proof

of Theorem 1.

Since

= C sin tr ² - i5 sin tr ² + iC cos tr ² + 5 cos tr ² - iC - 5 ) dt =

P(Y H <  r ) = P(Y H <  r 2 ) then by the inversion formula:

P (I ^YH ⁵ r 2 ) = F J ( r 2 ) ^- F YH < ⁰ > =

= 1 да 2 n

-да

--ln(1+(2 1 X k )²)

e

-------------( C sin tr ² + 5 cos tr ² - 5 ) dt +

t

+да

=2J

-да

- it 0      -i e - e

it

itr ²

— ^Ф| YH ⁽ t ) dt =

, +да

= 2^1

-да

1      - itr

1 - e

it

■2 да

П k=1

^{1 да}

+-- 1

2п J

-да

1 да e 4 £ ln(1 + (21Xk )2)

---k =1--------------- ( C cos tr ² - С - 5 sin tr ²) dt .

t

V1 - 2 it X k

dt =

The imaginary part is 0, since the integrand is odd and is considered on the entire axis (-да; +да). Then

, +да

=2П/

-да

1 — - itr

1 - e

it

да _______________

П .1 - 2 it X k л=1

dt =

P (| ^Y I H 5 r ’ ) =

1 +да

= 21 ; /

-да

1 - (cos tr ²

it

да ___________ isintr2) -ln П   2 itXk i tr ) e k=1         dt =

1 да

1 e

2п ^

-да

_; - 4ln(1+(2 1 X _k )²)

-------------( C sin tr ² + 5 cos tr ² - 5 ) dt .

t

We take into account the following:

, +да

=2^

-да

1 ^да

1 - (cos tr ² - i sin tr ²) -2 ^{£ ln(1,2} it ^{X k} ) , — ---------------- e ^{k + 1}        dt .

it

да

£ arctg2 1 X _k + 2 n k sin tr ² cos —-------------- +

Let us simplify the form of the function using the properties of the functions of the complex variable [4]:

ln(1 - 2 it X _k ) = ln 11 + 2 it X _k | + i (arg(1 - 2 it X _k ) + 2 n k )

да

£ arctg2 1 X k + 2 n k

, 2 •

+ cos tr sin —--------------

arg(1 - 2 it X k ) = arctg2 t X k + 2 n k .

Substituting, we obtain

1 +да

P fl ^Y I H ⁵ r ²) = .J

-да

i cos tr ² + sin tr ² - i ------------------x

t

да                               , да

^ ln(1+(2 t X _k )²) -2 i £ (arctg2 t X _k 2n k ) x e k ¹ e    ^k = 1                  .

Let us use the properties of the functions of the complex variable again:

1 ^да

—i ( £ arctg2 1 X 2 +2 л k ) e ^{2 k} = 1

да

£ (arctg2 1 X k + 2 n k )

= cos —------------

+ i sin

£ (arctg2 t X _k + 2 n k )

k =1

.

In the future, for the convenience of calculations we introduce the following notation:

£ (arctg2 1 X _k + 2 n k ) C = cos —------------

,

= cos

да

£ arctg2tX k + 2n k tr2 + —-------------

да

£ arctg2 t X _k + 2 n k

- sin —------------

= 2cos

tr2 + £ arctg2tX k + 2n k k=1

tr ² sin .

As a result, the formula will take the form:

1 да

2 n

-да

--ln(1+(2 1 X _k )²)

e ⁴      22

-------------( C sin tr ² + 5 cos tr ² - 5 ) dt =

t

= -да 2 n

-да

- -ln(1+(2 1 X _к )²) e ⁴

t

да tr2 + £ arctg2tX k + 2n k

£ (arctg2 1 X _k + 2 n k )

5 = sin k =1------------------

x

2cos

tr ² sin

dt =

.

=п

e

-да

. - 4ln(1+(2 1 X k )²)

t

The theorem is proved.

Thus, one can find the numerical values of the upper probability estimates P (| Y H <  r ) depending on the radius of the sphere r and the maximum eigenvalue X of the covariant operator R . Table was compiled for some values of r and X .

Upper numerical estimates in the case of Gaussian uptime of a computing system. Let

Knowing that the function is symmetric with respect to the origin of coordinates, we can write

„ да     - 4ln(l + ( ^{2 1 X} k ) 2 )

^P (I Y H ⁵ r ²) = _П J e----₁-----

-да

2п r2

J ( X , r ) = -J ^п 0

1 4 1 + 4 1² X

tr ² sin     dt .

If the random uptime of the computing system is a normal random field, then its distribution determined by the norm of the space C ( K ) can be estimated numerically from above. To do this, one only needs to know the value of the maximum eigenvalue X of the covariance operator R . Then using the embedding inequality [5] we have:

The theorem is proved.

The proof of Theorem 2. The practical use of Theorem 1 is difficult, since, firstly, the knowledge of all eigenvalues of Xk is assumed, and secondly, the integral sign contains infinite sums. Therefore, one has to confine oneself to estimates from above the studied probability. It's obvious that exp j - 1 Eln(1 + (2 1X k)2) f =1 • -да-----1

¹    k =1 П 4 1 + (2 1 X k )²

k =1

Let X = max _k >1 X _k , then

• ¹    П 4 1 + (2 1 x _k )^{2    1} 41 + (2 t ^X k ^{) 2}

k =1

• • -да5

¹ П 4 1 + (2 1 X k )^{2    1 4}1 ^{+ (2 1 X} k ^{) 2}

k =1

Consequently

2да 1

P"^r H < ^r ) ' 1 4_l . 4 1 2_/^smT ^d1.

Let us consider the integrand p (1) = —i 1     sin —.

141 + 412X2

r ²

It is obvious that lim ₁ , ₀ p ( 1 ) ^ — , and it means the

„ z x . , , ,             ,                     2пk function p(1) is a bounded one. p(1) =0 at 1 = —2-. The

r function graph is a sinusoid 1 ^ да, p(1) ^ 0 .

Hence

2п r2

P ( Y\_H <  r ) 5 - f ^{п J} 1 4 1 + (2 1 X )²

tr ² sin     dt .

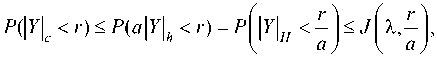
the constant a is equal to a fixed number, which is determined exactly depending on the number of variables d of the random field and the space H that is embedded in C ( K ).

Conclusion. This paper is devoted to the reliability of the computing system. One of the characteristics of the computing system reliability is the random number of its failures v ( r ). The distribution v ( r ) is the distribution of the sum of random times X i ( t ) of the failure-free operation of the computing system, i = 1, ..., n . It is impossible to write down the distribution v ( r ) explicitly. Therefore, one has to look for an estimate of these distributions from above. Assuming that the uptime X i ( t ) of the computing system is the sum of many variables, the authors of the paper obtained following results:

– it is shown that the problem of estimating the distributions of a random number of system failures can be considered as the problem of estimating the rate of convergence in the central limit theorem in Banach spaces;

– if there are certain restrictions on the uptime X ( t ) of the computing system, upper estimates are found for the distributions F n ( r ) of a random number of system failures. These estimates can be written as

F n ( r ) 5 J r—Tn j + cn ^e (ln n ) ^Y , I akjn )

where N ( r ) is the normal distribution, the constants a , c are determined earlier, the exponents p, у are determined by the conditions on X ( t ).

Numerical upper estimates of the form N ( r ) 5 J ( X , r ) are found for the normal distribution N ( r ).

2 п

2 r ²         1

^{P YН<Г} "^{n J} 1 4 1 + (2 1 X )²

tr ² sin dt .

The estimates obtained can be used for further research in the theory of computing systems reliability.

Upper probabilities for P ( Y_С)

r	X = 1	X = 2	X = 3	r	X = 1	X = 2	X = 3
0.1	0.0583	0.0415	0.0340	2.6	0.7586	0.6693	0.6034
0.2	0.1139	0.0817	0.0671	2.7	0.7659	0.6807	0.6161
0.3	0.1169	0.1200	0.0993	2.8	0.7724	0.6914	0.6282
0.4	0.2171	0.1580	0.1306	2.9	0.7783	0.7013	0.6397
0.5	0.2647	0.1941	0.1610	3,0	0.7836	0.7106	0.6506
0.6	0.3096	0.2289	0.1905	3.1	0.7884	0.7193	0.6610
0.7	0.3520	0.2624	0.2191	3.2	0.7926	0.7273	0.6708
0.8	0.3917	0.2945	0.2469	3.3	0.7965	0.7348	0.6801
0.9	0.4289	0.3253	0.2737	3.4	0.7999	0.7418	0.6893
1.0	0.4637	0.3549	0.2997	3.5	0.8029	0.7482	0.6972
1.1	0.4960	0.3831	0.3248	3.6	0.8057	0.7542	0.7051
1.2	0.5260	0.4101	0.3490	3.7	0.8082	0.7598	0.7125
1.3	0.5538	0.4358	0.3724	3.8	0.8104	0.7650	0.7195
1.4	0.5795	0.4603	0.3949	3.9	0.7124	0.7698	0.7261
1.5	0.6031	0.4836	0.4166	4.0	0.8142	0.7742	0.7323
1.6	0.6248	0.5057	0.4374	4.1	0.8159	0.7783	0.7382
1.7	0.6446	0.5266	0.4574	4.2	0.8173	0.7821	0.7437
1.8	0.6628	0.5465	0.4766	4.3	0.8187	0.7856	0.7489
1.9	0.6793	0.5653	0.4951	4.4	0.8199	0.7889	0.7538
2.0	0.6943	0.5830	0.5127	4.5	0.8210	0.7919	0.7584
2.1	0.7079	0.5997	0.5296	4.6	0.8219	0.7947	0.7627
2.2	0.7202	0.6154	0.5458	4.7	0.8228	0.7973	0.7668
2.3	0.7313	0.6302	0.5612	4.8	0.8224	0.7997	0.7706
2.4	0.7414	0.6441	0.5759	4.9	0.8237	0.8019	0.7742
2.5	0.7504	0.6571	0.5900	5.0	0.8251	0.8040	0.7776

The average number of system failures is да

H ( r ) = ^ F n ( r ), therefore, knowing the upper estimates n -1

for Fn ( r ), one can obtain upper estimates for H ( r ) and predict the level of average costs for the restoration of computing systems.