On the Performance of Priority-Based Virtual Channels Scheduling Algorithm in Packet Telemetry System

Published Online August 2011 in MECS

• I.    I NTRODUCTION

  With the development of space science and space technologies, some main worldwide space organizations established Consultive Committee for Space Data Systems(CCSDS) in 1982 to meet the demands of space missions[1]. Since then, CCSDS has designed a group of space communication standards, which are now widely used in more than 250 countries and regions[2-4]. Among these standards, TM Space Data Link protocol is a data communication and transmission protocol, which is mainly used(but not limited) in packet telemetry system to transmit packet telemetry data through the downlink, namely, from space to ground[5-7]. In order to transmit those information better, a two-layer multiplexing mechanism is used in packet telemetry system, which includes packet channel multiplexing mechanism and virtual channel multiplexing mechanism. Packet channel

  Manuscript received April 6, 2010; revised June 1, 2008; accepted July 1, 2008.

multiplexing mechanism makes a certain number of data packets share a virtual channel(VC), while virtual channel multiplexing mechanism makes a certain number of virtual channels share a physical channel.

Virtual channels are a group of logic channels formed by dividing the physical channel by different time slots. Each virtual channel transmits the packets information with the same or similar service demands, and the physical channel is shared by all these virtual channels. Thus the physical channel can be used to transmit various upper-layer sources data stream with different types and transmission requirements. The algorithm used in virtual channels mechanism, namely, virtual channels scheduling algorithm, determines the sequence of occupying the physical channel by each virtual channel, which has a great effect on the transmission delay and efficiency. In Packet Telemetry System, the scheduling algorithms often used include mainly fist-in-first-out algorithm, maximum remained prior algorithm, polling algorithm, priority-based algorithm. In some complicated systems, dynamic-priority-based algorithm may be used.

In this paper, we study the priority-based virtual channels scheduling algorithm in packet telemetry system. For this algorithm, each VC is assigned a priority number according to its importance and real-time requirements before the system begins to work. The important the VC is, or the higher the real-time required by the VC is, the higher the priority assigned will be. At each scheduling time point, the one with the highest priority among the VCS whose frames buffer does exist frames can be scheduled, and the first frame in its buffer is transmitted through the physical channel(namely, the VC occupies the physical channel). Through theoretical analysis and simulation results, we find an interesting conclusion: when the running time of the scheduling module is long enough, for the VC with the highest priority, both the probability of being scheduled and the packets losing rate converge on fixed values, which can provide reference for engineering design.

in Packet Telemetry System

• II.    S YSTEM M ODEL

In this paper, we choose the packet telemetry source model, of which the physical channel is divided into 4 virtual channels to transfer all user data through the downlink[8], as illustrated in Fig.1. The 4 virtual channels are shown as follows:

VC1: transmitting general engineering data, with the second higher priority.

VC2: transmitting important express data, with the highest priority.

VC3: transmitting download data, with the lowest priority.

VC4: producing idle frames. At any scheduling time point, if there are no frames in all the other VCs buffers , an idle frame is generated in VC4 buffer and transmitted through the physical channel.

For VCi, i = 1,2,3 , the packet arriving process is Poisson distribution with the parameter λi , and the packet length is a fixed value[9]. Let lpi be the Packet length, and lmp be the MPDU packet zone length of the frame, then each frame contains N = l /l packets, i mp pi which also means that a frame is generated and sent to the VCi buffer at the arriving time of the mNi packet, m = 1, 2, 3L .

At each scheduling time point, the scheduling module choose the one with the highest priority among the VCs whose frame buffers are not empty, and transmit the first frame in its buffer through the physical channel. If buffers of VC1, VC2, VC3 are all empty, an idle frame is generated in VC4 buffer and transmitted

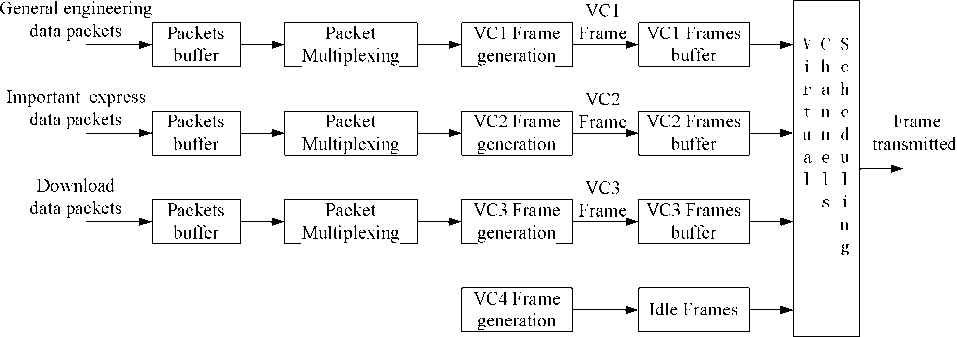
Figure 1. Packet Telemetry Source Model

Substituting equation (2) into equation (1), we can get

• III.    T HEORETICAL A NAYSIS

• A. the size of packets buffer is infinte

First consider the condition that the size of packets buffer is infinite. At the first scheduling time point, Δ t , if there is one frame or more in the VC2 frames buffer, which means the number of packets arriving in the packets buffer during the time interval [0, Δ t ] is larger than or equal to N ₂ , VC2 can be scheduled. So we can get the probability of VC2 can be scheduled at the time A t , P VC2 (1] , as

^PIVC 2 (1) = P ( A vc 2 (A t ) >  N ₂)

∞

= ∑ P ( A VC 2 (∆ t )= n ) n = N ₂

where A_{VC 2} (Δ t ) means the number of packets arriving in VC2 during the time interval [0, Δ t ] . For the packet arriving process which obeys Poisson distribution, the probability of arriving n packets during the time period Δ t , P ( A_{VC 2} (Δ t ) = n ) , can be calculated as:

P ( A VC 2 (∆ t ) = n ) = ^{( λ 2 ∆ t ) n e - λ 2 ∆ t} (2) n !

P C 2 (1^ ^A— n = N 2         n ^!

Otherwise, if the number of packets arriving in the packets buffer during the time interval [0, Δ t ] is less than N ₂ , there will be no frames in VC2 buffer at the time Δ t , and VC2 cannot be scheduled. So we can get the probability of VC2 can be scheduled at the time Δ t , P ivc 2 (0] , as

^PIVC 2 (0) = P ( A vc 2 (A t ) <  N 2 )

^N 2 ^{- 1}                                (4)

= ∑ P ( A_{VC 2}(∆ t ) = n )

n = 0

Substituting equation (2) into equation (4), we can get

N ₂ - 1

Pivc2' (0)= £ n=0

( λ ₂∆ t ) ⁿ e ^{- λ 2 ∆ t} n !

For the size of packets buffer is infinite, there will be no packets lost. The packets not transmitted at the time Δ t will be stored in the packets buffer. Let R_{I 1} be the number of packets remained in VC2 packets buffer after the time Δ t , P ( R_{I 1} = r ) be the probability of R_{I 1} = r . If

On the Performance of Priority-Based Virtual Channels Scheduling Algorithm in Packet Telemetry System r = 0,1, 2,L N - 1 , r packets remained means that during the time interval [0, At] , there are N2 + r packets arriving(in this case, VC2 is scheduled, N2 packets transmitted and r packets remained) or r packets arriving (in this case,VC2 is not scheduled, all of the r packets remained ), so we have

P ( R i 1 = r ) = P ( A VC 2 ( A t ) = N 2 + r ) + P ( A VC 2 ( A t ) = r )

r = 0,1,L, N ₂ -1(6)

If r = N ₂, N ₂ + 1,L да , r packets remained means that during the time interval [0, A t ], there are N ₂ + r packets arriving(VC2 is scheduled, N ₂ packets transmitted and r packets remained), so we have

P ( R i 1 = r ) = P ( A VC 2 ( A t ) = N 2 + r )

= ( ^ 2 A t ) N ^{+ r}e - " 2 ^a t

=    ( N ₂ + r )!

Substituting equation (2) into equation (6), we can get r = N2,N2 + 1,L да

P ( R i 1 = r ) =

( ^ 2 A t ) N ^{+ r}e - " 2 ^A t + ( ^ 2 A t ) ^re~ " 2 ^A t

( N 2 + r )!

r !

Combing equation (7) and (8), expressed as

P ( R I 1 = r ) can be

r = 0,1,L, N 2 -1(7)

(Л 2 А t ) ^{N 2 + r} e

P ( R i i = r ) = ^

( N 2 + r )!

(Х 2 А t ) ^{N 2 + r} e~ ^ 2 ^A t

( N 2 + r )!

" 2 ^A t + (Л 2 А t ) ^r e - " 2 ^A t

r !

r = 0,1,L N ₂ -1

r = N ₂, N ₂ + 1,L ,да

At the second scheduling time point, 2A t , if the total number of the packets remained at the time A t , R I 1 ,and the new packets arriving in the time interval [A t , 2A t ], A VC ₂(A t ), is larger than or equal to N ₂, there will be at least one frame in the VC2 frames buffer, and VC2 can be scheduled. Otherwise VC2 cannot be scheduled. Thus we can get the probability of VC2 can be scheduled at the time 2A t , P_{IVC 2}'' (1) ,as

^PIVC 2 '(1) = P ( R i i + a vc 2 (A t ) >  N 2 )

« *                      (10)

= E E ^{P ( R}i 1 = ^{r ,} a vc 2^{( a} t ) = q ^{- r} )

q = N 2 r =0

For Poisson distribution, RI 1 and AVC2(At) are independent of each other, so we have да q

P ivc 2'' (1) = E E P ( R i 1 = r , A VC 2 (A t ) = q - r )

q = N 2 r =0

да q

= EE ^{p ( R}i 1 = ^r ) • ^{P (} a vc 2^{( a} t )= q ^{- r} )

q = N ₂ r =0

The

probability of VC2 cannot be scheduled at the time 2At, PIVC2 (0), can be calculated as

N 2 -1 q

P ivc 2'' (0) = E E P ( R i 1 = r , a vc 2 ( A t ) = q - r )

_N q =_-0₁ r =0                                       ₍₁₂₎

= E E p ( R i 1 = r ) • P ( a vc 2 (A t ) = q - r )

q =0 r =0

Let RI2 be the number of packets remained in VC2 packets buffer after the time 2At , P(RI2 = r) be the probability of RI2 = r .If r = 0,1,2,L N -1 , r packets remained means that the total number of the packets remained at the time At, RI 1 ,and the new packets arriving in the time interval [At, 2At], AVC2 (At), is N2 + r (in this case, VC2 is scheduled at the time 2At , N2 packets transmitted and r packets remained) or r (in this case,VC2 is not scheduled at the time 2At, all of the r packets remained ), so we have where the values of P (AVC 2(A t) = q - r) and P( Ri 1 = r) can be calculated by using equation (2) and equation (9), respectively.

P ( R i 2 = r ) = P ( R i 1 + A VC 2 ( A t ) = N 2 + r ) + P ( R i i + a vc 2 ( A t ) = r )

N ₂ + r

r

= E ^{P ( R}i 1 = q ^, a vc 2^{( a} t ) = ^N 2 ^{+ r -} q )⁺ E ^{P ( R}i 1 = q ^, A Vc 2^{( A} t ) = ^{r -} q )

q =0 N ₂ + r

q =0

r

= E P ( R i 1 = q ) • P ( A VC 2 ( A t ) = N 2 + r - q ) + E P ( R i 1 = q ) • P ( A VC 2 ( A t ) = r - q )

q =0

q =0

r = 0,1,L, N ₂ -1

On the Performance of Priority-Based Virtual Channels Scheduling Algorithm in Packet Telemetry System

If г = N2,N2 + 1,L да, г packets remained means that    p(R the total number of the packets remained at the time I2

A t , R I 1 ,and the new packets arriving in the time interval

[At, 2At] , AVC2(At), is N2 + г (VC2 is scheduled at the time 2At , N2 packets transmitted and г packets remained), so we have

^г ) = ^P ( ^RI 1 ^{+ A}VC 2 ^{( A} t ) = ^N 2 ^{+ г} )

= N f ' p ( R i i = q , A c 2 ( A t ) = N 2 + г - q )    (14)

q =0

= N f ' P ( R i i = q ) ■ P ( A_V c 2 ( A t ) = N 2 + г - q )

q =0

г = N ₂, N ₂ + 1,L да

Combining equation (13) and (14), P ( R I ₂ = г ) can be expressed as

P ( R i 2 = ' )

N2 + г                                                           г f p(Ri 1 = q) ■p(Avc2(At) = N2 + ' - q) + f p(Ri 1 = q) ■p(AC2(At) = ' - q),

г = 0,1,L N ₂ - 1

q =0

f ' P ( R i 1 = q ) ■ P ( A vc 2 ( A t ) = N 2 + г - q ),

q =0

q =0

г = N ₂, N ₂ + 1,L да

Similarly, at the kt h scheduling time point, k A t , if the total number of the remained packets at the time ( k - 1)A t , R_Ik _ j , and the number of packets arriving during the time period [( k -1) A t , k A t ], A_{VC 2} (A t ), is larger than or equal to N ₂ , there will be at least one frame in the VC2 frames buffer. Thus VC2 can be scheduled. Otherwise VC2 cannot be scheduled. So at the time k A t , the probability of VC2 can be scheduled, P_{IVC 2} ^{( k )} (1) , and the probability of VC2 cannot be scheduled, P_{IVC 2} ^{( k )} (0) , can be expressed as

P ivc 2^{( k} ) (1) = P ( R ik -1 + A vc 2 (A t ) >  N 2 ) да q

= f f P ( R ik -1 = ' , A vc 2 (A t ) = q - г )    (16)

q = N 2 г =0

да q

= f f P ( R ik -1 = ' ) ■ P ( A vc 2 (A t ) = q - г )

q = N ₂ г =0

P ivc 2( k ) (0) = P ( R ik -1 + A vc 2 (At ) <  N 2 )

N 2 -1 q

= f f ^{P ( R}ik -1 = ^г , a vc 2 ^{( A} t ) = q ^{- г} )     ⁽¹⁷⁾

q =0 г =0

N 2 -1 q

= f f P ( R ik -1 = ' ) ■ P ( A vc 2 (A t ) = q - г ) q =0 г =0

k = 3,4Lда

Let R k be the number of packets remained in VC2 packets buffer after the time kAt , P(R k = г) be the probability of R k = г , using the method of getting equation (15), we can get p (Rk = г) = ^

N2 + г                                                             г f P(Ra-1 = q) ■P( avc 2(A t) = N2+г - q)+f P (Ra-1 = q) ■P ( avc 2(A t) =г - q),

г = 0,1,L N ₂ - 1

q =0

N2 + г f P(Rft-1 = q) ■ P(avc2 (At) = N2 + г - q),

. q =0

q =0

г = N ₂, N ₂ + 1,L да

k = 3,4L да have the probability of VC2 occupying physical channel at the time At, PVC2 (1), as

P vc 2' (1) = P ( A vc 2 (A t ) >  N 2 ) = f^ ^{( A} 2 ^A t ) n e " 2 " t   (19)

n = N ₂         n !

where A_{VC 2} (A t ) means the number of packets arriving in VC2 during the time interval [0, A t ], whose value can be calculated by equation (2).

Otherwise, there will be no frames in VC2 frames buffer, which means VC2 can not occupy physical

On the Performance of Priority-Based Virtual Channels Scheduling Algorithm in Packet Telemetry System channel. So we have the probability of VC2 not occupying physical channel at the time At, PVC2 (OJ, as

N 2 -1 / 3 Л n — A 2 A t

P vc 2‘ ( 0 ) = P ( A vc 2 (A t ) <  N 2 ) = I 1 ——---- (20)

n = 0          n !

-Ie - A2A t (A2 At)n PVC 2( d ) =^ n=0         n ! e - A2A t (A2 At)M+d (M + d)! d = 0

d = 1,2,L ,да

Let M be the capacity of the VC2 packets buffer, probability of losing d packets of VC2 at the time A t , P _{lVC 2} ( d ) ,can be expressed as:

After the first scheduling time point, probability of r packets remained in VC2 packets buffer, P_{RVC 2}^' ( r ) , is

( A ₂ A t ) ^{N 2 + r}

e ^A 2 ^A t

( N 2 + r )!

+

( A 2 A t )

r

e

A 2 A t

да

r

!

r = 0,1,L , M

N 2

P ^R VC 2

'^{( r} ) = ’

I

i = M

( Л 2 A t ) i e

A 2 A t

i

!

+

( a ₂ a t ) ^{M - N 2}

e

A 2 A t

( M - N 2 )!

r = M

N 2

( A ₂ a t ) ^r e

A 2 A t

r

!

M

-

N 2 <  r < N 2

others if N2 < M < 2N2;

Pr  ' ( r ) =

^R VC 2

(A ₂ A t ) ^N 2 ⁺ re ~ ^A 2 ^A t     (A ₂ A t ) re ~ ^A 2 ^A t

( N ₂ + r )!    ⁺ r !

(A ₂ A t ) ^{N 2 +} re "  ^A 2 ^A t

( N 2 + r )!

да

I i=M

(A2-t)^e A i!

r = 0,1,L , N ₂ -1

N ₂ -1 <  r <  M - N ₂

r = M - N2

others

if M > 2 N ₂

Similarly, at the kt h scheduling time point, k A t , k = 2,3L , when the total number of the packets remained after the time ( k -1)A t , R_{VC 2}(( k - 1)A t ) , and the packets arriving during the time interval [( k - 1)A t , k A t ] , A VC ₂(( k - 1)A t , k A t ) , is larger than or equal to N ₂ , there will be at least one frame in VC2 frames buffer. In this case, VC2 can be scheduled and the first frame in its buffer is transmitted through the physical channel, otherwise it cannot be scheduled. Thus we can get

P vc 2^{( k} ) ( 1 = P( ([ R vc 2 (( k - 1) A t ) + A vc 2 (( k - 1) A t , k A t )] >  N 2 ) да q                                               (24)

= II Prvc 2 ^{( k - 1)} ( i ) P ( A ( A t ) = q - i ) q = N 2 i =0

P vc 2⁽ k ) (0)= P ([ R vc 2 (( k - 1) A t ) + A vc 2 (( k - 1) A t , k A t )] <  N 2 )

N 2 -1 q                                                 (25)

= II Prvc 2 ^{( k - 1)} ( i ) P ( A vc 2 ( - 1 ) = q - i ) q =0 i =0

where P_{VC 2} ^{( k )}( 1) and P VC 2 ^{( k )} (0) are the probability of VC2 can be scheduled and cannot be scheduled at the time k A t , respectively.

Probability of losing d packets of VC2 at the time k A t can be expressed as:

in Packet Telemetry System

P ⁽ k ) ivc 2 ( d ) ^

Mq

УУ P r c 2 ⁽ k ^{- 1)}( i ) P ( A vc 2 (A t ) = q -i ) q = 0 i = 0

d = 0

M + d

У P r_vc 2 ^{( k} ( q ) P ( A vc 2 t ) = M + d - q ) d = 1,2,L to

_ q = 0

After the kth scheduling time point, probability of r packets remained in VC2 packets buffer is

N 2 + r                                                    r

У P r_{vc 2} ^{( k - 1)}( q ) P ( A vc 2 (A t ) = N 2 + r - q ) + У P r_{vc 2} ( k ^{- 1)}( q)P ( A vc 2 (A t ) = r - q )      r = 0,1,L , M - N ₂ -1

P_R  ⁽ k ) ( r ) =

^R VC 2

q = 0

to i

У ( У P r vc 2

i = M q = 0

Vp ( k - 1),

У ^R VC 2    '

q = 0

q = 0

M - N 2

^{( k} ' i q ) P ( A vc 2 (A t ) = i - q )) + У P r_{vc 2} ⁽ k 4 q ) P ( A c 2 M - N 2 - q )   r = M - N 2

q = 0

⁽ q ) P ( a vc 2⁽ A t ) = r ^- q )

M - N ₂<  r <  N ₂

others

if N 2 <  M < 2 N 2 ;

■ N ₂ + r                                                                 r

У P r_vc 2 ^{( k - 1)} ( q ) P ( A vc 2 (A t ) = N 2 + r - q ) + У P r_cc 2 ⁽ k ^{- 1)} ( q ) P ( A vc 2 (A t ) = r - q ) r = 0,1, L , N 2 -1

q = 0                                                            q = 0

Pr  ⁽ k ) ( r ) =

^R VC 2

N ₂ + r

У P r_{cc 2} ⁽ k ^{- 1)} ( q ) P ( A vc 2 (A t ) = N 2 + r - q ) q = 0

to i

У ( У P r cc 2 ⁽ k ^{- 1)}( q ) P ( A vc 2 (A t ) = i - q ))

i = M q = 0

N ₂ -1 <  r <  M - N ₂

r = M - N2

others

if M > 2 N ₂

• IV.    S IMULATION R ESULTS

Simulation parameters are set as follows:

• (1)    Source data rate of VC1, VC2 and VC3 are taken 10,10, 35 Mbps, respectively;

• (2)    The MPDU packet zone length of frame, l_mp , is 10000bits;

• (3)    The packet length of VC1, VC2 and VC3 are 1000, 2000, 500bits, respectively;

• (4)    The average packet arrival rate of VC1, VC2 andVC3 are 10000, 5000, 70000/s, respectively;

• (5)    The total simulation time T is 0.8s.

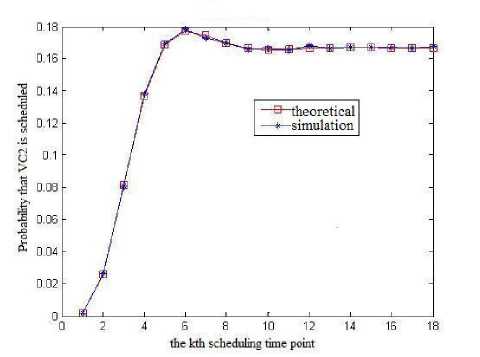
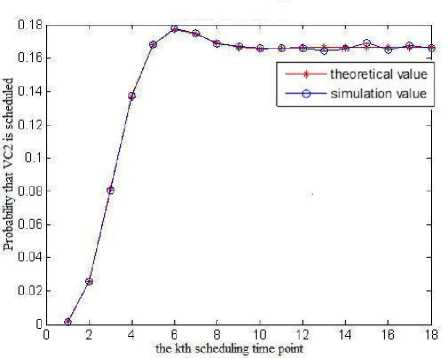
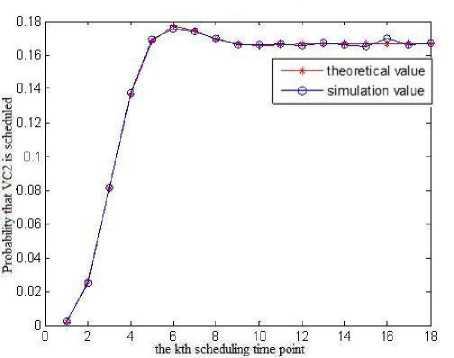
Fig.2 illustrates the probability that VC2 is scheduled at different scheduling time points.

k = 2,3L to

(a) M is infinite

On the Performance of Priority-Based Virtual Channels Scheduling Algorithm in Packet Telemetry System

(a) Probability of losing 0 packet

(b) N 2 < M <  2 N ₂( M = 8, N 2 =5)

(b) Probability of losing 1 packet

(c) M > 2 N ₂( M = 15, N 2 =5)

Figure 2. Probability that VC2 is scheduled at different scheduling time points

From the simulation results we can see that with the increasing of the running time of the scheduling module, the probability that VC2 can be scheduled converges on a fixed value, and the simulation curve almost completely coincide with the theoretical curve, which proves the correctness of the analysis in section III.

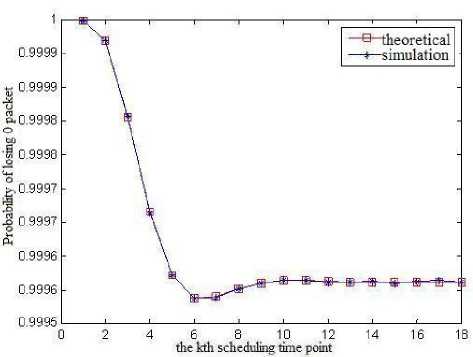
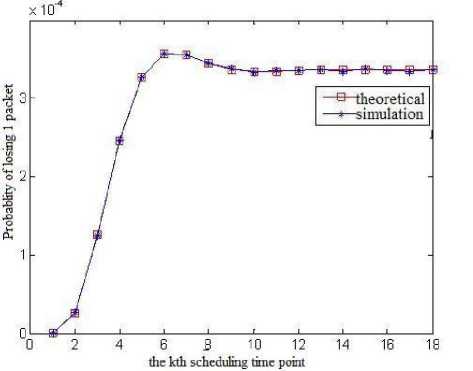
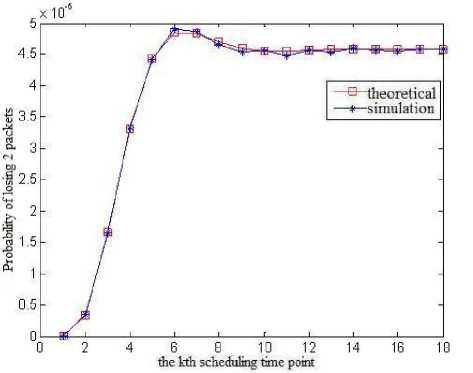
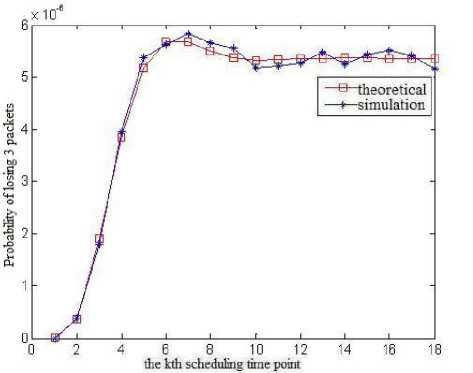
Fig.3 illustrates the curve of the theoretical value and simulation value of the packets losing rate of VC2 at different scheduling time points when the packet buffer capacity is M ( M = 8), which proves the correctness of equation(26). In practical application, one can design the value of M according to the desired packets losing rate.

(c) Probability of losing 2 packets

in Packet Telemetry System

• (d) Probability of losing 3 packets

Figure.3 Packets losing rate of VC2 at different scheduling time point

• V.    C ONCLUSION

We study the scheduling algorithm based on priority in packet telemetry system. Through severe reasoning and simulation experiment, we find that when the running time of the scheduling module is long enough, the probability that the VC with the highest priority can be scheduled converges on a fixed value. We also propose the method to calculate packets losing rating of the VC with the highest priority, which can offer reference to engineering design.

A CKNOWLEDGMENT

This work was supported by the State Key Laboratory of Rail Traffic Control and Safety(RCS2009K008), Beijing Jiaotong University and Doctorial Start-up Foundation for Scientific Research of Liaoning Province(20101092).