On the possibility of flight of a single-stage rocket to the planets of the Solar system

The concept of rockets using LPE s, laid down by Valentin Petrovich Glushko (USSR) and Wernher von Braun (Germany), has hardly changed to this day, which is proved by the use of designs invented back in the 1950–1960s. The main design differences are determined by the fuel and an oxidizing agent being used [1–3]. The products of combustion are superheated water vapor, carbon dioxide and nitrogen; when using liquid hydrogen and oxygen, only superheated water vapor is released. At present, the efficiency of delivering heavy loads to near-Earth orbit is insufficient, and all possibilities for increasing it are practically exhausted. For example, the Proton M rocket with the all-up-weight of 705 tons launches a load of 23.7 tons into the orbit of 220 km, which is 3.4%. For the altitude of 36,000 km, the payload is 3.3 tons, or 0.5% of the all-up-weight. It is necessary to take into account the damage caused to the environment when using certain types of fuel and oxidizer, so the promising Angara-

A5M rocket will operate on a well-known fuel mixture of kerosene with oxygen, but with greater efficiency.

The difference in the value of the specific impulse (Isp) of engines based on fuel from kerosene and oxygen, in comparison with the best cryogenic hydrogen-oxygen engine, is no more than 17%. Nevertheless, given the aggregate parameters for the rocket as a whole, their difference in the efficiency of delivering cargo into orbit is much less. Numerous tests of oxidizers, fuel, and development of new engines with various types of combustion chambers did not lead to a significant increase in the Isp of engines [2] for environmentally friendly fuel. Therefore, it is necessary, using the totality of scientific and technological achievements of recent decades, to multiply the Isp for LPEs, which will significantly increase the efficiency of cargo delivery to near-Earth orbits and, as a result, will make it possible to start flights to other planets of the solar system at higher speeds than currently. This paper proposes a more significant use of electrical energy to increase the Isp of fundamentally new, small-sized engines for rockets launched from the earth's surface. The concept of building rockets changes significantly when using powerful sources of electrical energy to increase the Isp. Currently, electricity for thrust is practically used in small-sized, ion and magneto-plasma engines with low thrust, which is unacceptable for rockets launched from the Earth's surface.

Influence of technical parameters on the efficiency of rocket flight

In accordance with the calculation according to the formula by K. E. Tsiolkovsky for the flight of a rocket outside the fields of gravity, the following average values of the Isp were taken: for a typical rocket engine - 3 km / sec; for the LPE with heating of supersonic gas flows by plasma - 4.5 km / sec. The limit of the increase in Isp is determined mainly by the amount of electric power being used in the LPE and can increase significantly depending on the design of the rocket as a whole. The redistribution of part of the fuel being used, which is up to 90% of the all-up-weight, for the production of electricity is compensated by a significant increase in the Isp for the LPE with an increase in the speed and overall efficiency of the rocket flight. The comparison shows that an increase in Isp by 1.5 times gives a decrease in the initial weight of a rocket for an engine with plasma heating by ~2.4 times for the first space velocity, ~3.5 times for the second space velocity, and ~6.4 times for the third space velocity. Thus, the flight efficiency of a rocket increases significantly with the growth of the Isp, which is now limited by the weight and power of the electric generator. The prospective prototypes of electric generators MEG-6NS and MEG-15NS that have weight of 4.5 and 9 kg, a power of 6 and 15 kW, respectively, by NaukaSoft, allow us to produce in the future such a small-sized LPE. The ratio ηт = Mт/Мк is of great importance for the weight of Mt fuel being used to the weight of an unfueled rocket with the Mk payload to achieve the appropriate speed. For example, for the heavy rockets Proton M and Zenit this ratio is ηt ≈ 9.26–7.94 for a flight to an orbit with the height of 220 km, which is much higher than the theoretical optimal value ηt ≈ 4 obtained by the academician Ya. B. Zeldovich in 1963. The limit for increasing speed is the overload for the crew of a manned rocket, while the cargo version of the rocket allows achieving large overloads and, therefore, is more efficient in terms of fuel use. 4-5 engines are normally used in one cluster. Moreover, they have a large diameter due to the profiled Laval nozzle being used. The use of small-sized LPEs with plasma heating from a combined set of cells provides an additional advantage - the influence of parasitic air flows between individual exhaust jets of an LPE at high pressures near the earth's surface, which decreases the overall jet thrust, is reduced. This is explained by an increase in bottom pressure due to a smaller inactive area for outflowing gases, when the length of the air flow path to the center of the cluster of many small engines increases sharply. The important parameters for an LPE are the temperature ТСP and the pressure РCP in the combustion chamber, which are interconnected. For example, if the pressure in the combustion chamber is increased by 50 times, then this will lead to a temperature increase by 15%, which will increase the consumption complex by only 3% for fuel from kerosene with nitric acid. Therefore, LPE designers took the path of increasing the expansion ratio of the nozzle ƐC in terms of pressure. This makes it possible to increase the Isp in vacuum by 1.15 times with an increase in ƐC by 50 times. But such a path led to the large dimensions of the profiled Laval nozzle being used and to a decrease in the efficiency of the rocket's flight as a whole in dense layers of the atmosphere. Another way to increase the efficiency of LPEs is to increase the specific gravity of the fuel, although its doubling allows increasing the so-called fuel carrying capacity by only 20% [3], but this method is also limited by a small choice of fuel, oxidizer and fuel additives. For example, in [4] it is proposed to use a three-component fuel: kerosene with metal additives, liquid hydrogen and liquid oxygen. But the increase in Isp, in this case, according to the calculations, is no more than 6.5% for the operation of a rocket engine in a void. It is also impossible to significantly increase the Isp by simply increasing the calorific value of the fuel, since the maximum gas velocity in the estimated section Wг max is proportional to the square root of the limited calorific value of the Qт fuel. For example, in order to increase Wг max =3182 3182 m / sec to 4000 m / sec or 1.257 times, it is necessary to increase Qт by 1.58 times, i.e. by 58%. For a multiple increase in Isp, as the most important parameter, it is proposed to additionally heat the supersonic gas flow in a conical nozzle by a powerful electromagnetic RF field based on the works [5; 6], where it is proposed to increase the efficiency of combustion of modified fuel and a new type of oxidizer at an increased pressure of atoms and molecules in a high-speed combustion chamber. It is clear that the higher the pressure in the combustion chamber, the higher the temperature obtained in it, the more complete the degree of fuel combustion, and the greater the Isp at the exit of the conical nozzle. Nev-ertherless, the weight calculation shows that the available power generators MEG-15NS (2 generators simultaneously) can be used at a pressure in the combustion chamber up to ~15 MPa, which limits their use. The rejection of the profiled Laval nozzle in favor of a conical nozzle with a maximum expansion coefficient of no more than 200–250 in area (3000 in pressure) is due to the special design of the LPE due to the proposed use of built-in, pulsed gas ionizers with intense X-ray radiation [7]. Fig. 1 shows a simplified diagram of a small-sized LPE, proposed here for construction according to a new concept.

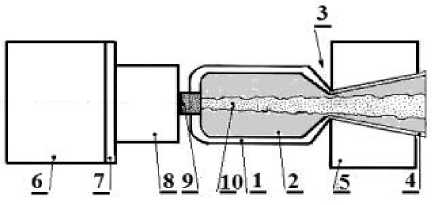
Рис. 1. Упрощённая схема ЖРД:

1 – корпус КС; 2 – горячие газы; 3 – критическое сечение; 4 – конус; 5 – ВЧ ионизатор;

6 – генератор электроэнергии; 7 – изолятор, 8 – ионизатор; 9 – анод; 10 – рентгеновские кванты

• Fig. 1. Simplified scheme of liquid-propellant engines:

• 1    – combustion chamber body; 2 – hot gases; 3 – critical cross-section; 4 – cone; 5 – RF ionizer; 6 – electricity generator; 7 – insulator; 8 – ionizer; 9 – node; 10 – X- ray quanta

The power of one ionizer for the combustion chamber, partially using the Compton Effect for X-ray quanta, is up to 1 MW per pulse, but the total average power is 0.50–0.75 kW. The area of the grounded anode 9 is approximately equal to the area of the critical section F Cr . It has long been known that the ionization of gases significantly improves the combustion process of any fuel [8] due to the formation of free radicals and electrons, which increase the activity and speed of combustion processes in chemical reactions of atomic oxidation for the fuel being used. But the main task of the proposed ionizer built into the combustion chamber is to increase the conductivity of the supersonic gas flow at the inlet of the plasma-heated electromagnetic RF field with high power density in the conical nozzle 4, which should far exceed the specific power of the fuel burned in the combustion chamber.

Simplified theory of the using an electromagnetic RF field

In the paper by G. N. Abramovich [9], a similar problem of additional heating of the gas by an external source was considered, but the final negative result for practical use was obtained for a straight cylindrical pipe, and not for a conical nozzle. Let us consider the theory of ongoing processes for the conical nozzle of the LPE, based on the calculation of the maximum energy of plasma heating of the supersonic gas flow over the entire length of the conical nozzle. For the energy flow in an expanding conical nozzle and in the absence of heat exchange with the external environment, technical work and internal friction, without taking into account the potential energy for gases, the generalized Bernoulli equation has the following form [9]:

where p – gas pressure, n/m²; ρ – gas density, kg/m³; w – gas velocity, m/sec; i = C P T – heat content, J/kg; C P – specific heat capacity, J/kg ºK; T – temperature, ºK. The indices 1 and 2 mean the initial and final state of the gas. The first additive component is related to the kinetic energy, the second one - to the static pressure, and the third one - to the heat content of the gas flow due to external heating. Let us introduce the following relationship: ( a Cr )² = k · p 1 /ρ 1 is the square of the gas velocity, where a Cr is the gas velocity in the critical section F Cr ; k is an indicator of the polytropic process of expansion and heating of the gas flow. Let us assume, in the first approximation, that С Р2 ≈ С Р1 ≈ С Р , and heating Т 2 – Т 1 ≈ ∆ Т . The solution for equation (1) is found at p /ρ ^k = соnst, in the form of a total sum, including both solutions for the integrals:

Next, we transform (2) taking into account the relations p 1 = p Cr , p 2 = p C ; Ɛ C = p Cr / р C , Ɛ C is the degree of expansion of the gas flow in the nozzle. We also have w 1 = a Cr ; λ c = w 2 / a Cr – the dimensionless gas flow velocity in the nozzle, then we obtain the equation in the dimensionless form

To solve the integral in the equation (3), we make the following simplifying assumptions: the temperature along the entire conical nozzle increases from Т Cr to the maximum Т max and then decreases to a certain value Т min ≥ Т Cr , and the dependence is quadratic or close to linear. Let us introduce the following constants: L C = h / R Cr , where L C is the reduced dimensionless length of the nozzle, h is the length of the heated part of the nozzle, m; R Cr is the radius of the critical part of the nozzle, m; f C = F C / F Cr is the expansion ratio of the nozzle, where F C is the section in any part of the nozzle, m². Then, after simple transformations, taking into account the fact that the definite integral in the equation (3) is a certain number β, we obtain the final form of the equation:

where tg(α) – tangent of the angle of inclination of the conical nozzle; β = 2/3 for the quadratic dependence Т = Т ( х ) or β = 1 for the linear one. In the absence of external heating of the EM field, Т max = Т Cr and the formula (4) coincide with the well-known formula by G. N. Abramovich [9]. The results of the calculations using the formula (4) are shown in fig. 2 for a nozzle without heating, i.e. at Т max = Т Cr for the values of the index of the polytropic expansion process k in the range from 1.10 to 1.30.

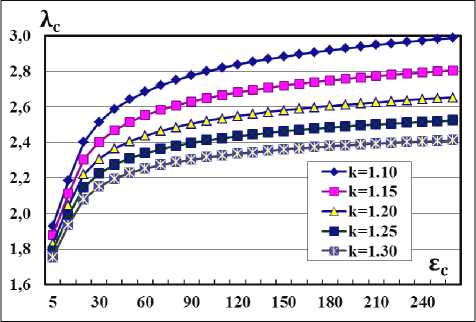
Рис. 2. Зависимость относительной скорости газов λ C в коническом сопле от коэффициента расширения сопла по давлению Ɛ C

Fig. 2. Dependence of the relative velocity of gases λ C in a conical nozzle on the expansion coefficient of the nozzle by pressure Ɛ C

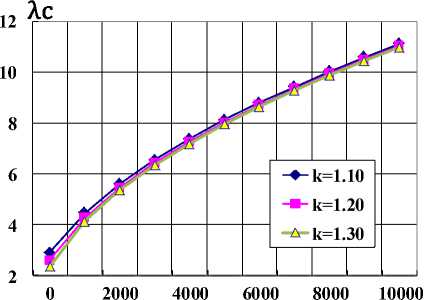
It can be seen that for the values Ɛ C ≥ 100, the relative velocity tends to saturation; therefore, it is possible to choose the value of ε C in the range from 100 to 200 determined mainly by design conditions. The value k = 1.10 corresponds to monatomic gases, and k = 1.30 corresponds to polyatomic gases. Real gases during the combustion of fuel mixtures are a complex sum of monatomic, diatomic and polyatomic molecules, therefore these calculations are approximate, but they describe the processes occurring in gas flows quite well. Additional heating of the supersonic gas flow by plasma leads to dissociation of polyatomic molecules and an increase in the proportion of monatomic molecules, which reduces the value of the k index, increasing the relative velocity λ C and the efficiency of the thermal expansion process of gases in the nozzle and the entire LPE as a whole. It follows from the calculations that even for a relatively small plasma heating of a supersonic gas flow at 1000 ° C, the relative velocity of gases λ C increases significantly to a value of 4.2–4.4, which corresponds to the Isp for liquid hydrogen and oxygen. Fig. 3 а shows the results of the calculations according to the above formulae for the dependence of the relative velocity λ C on the amount of gas heating along the entire length of the conical nozzle. The parameters corresponded to the fuel mixture of kerosene with nitric acid, in the heating range up to 1000 ° C, at f C = 25; L C = 25 (for R Cr = 6 mm, h = 0.15 m); ε C = 150; α = 9º, a Cr = 1026 m/sec; C P = 1.8 kJ/kg. Fig. 3 b shows the calculation results for a larger amount of nozzle gas heating up to 10000 ° C. It can be seen that the relative velocity of gases increases to the value of λ С = 11, which corresponds to the velocity of about ~ 10 km/sec. The dependence of λ С on the value of k decreases with increasing heating, as the concentration of atoms and diatomic molecules increases.

With the volume of the combustion chamber V СP = (2.5–2.7)∙10^–4 m³ and the possible cross sections F Сr = (0.7854–0. 5027)∙10^–4 m², the value of the reduced length of the combustion chamber L Cp = V Cp / F Cr can reach 3.4–5.2 m. Such a high L Cp indicator will contribute to more complete burning of fuel in the combustion chamber and an overall increase in Isp, respectively. Since the nozzle area adjacent to the F Cr section is significantly reduced, the heat flow through the walls also decreases, which will increase the temperature and velocity of the gas flow through the cooled nozzle. It can be noted that Meck-er [10] achieved a high heating temperature Т max = 5. 2∙10⁴ ºК for plasma compressed in a channel with the diameter of 2.3 mm at atmospheric pressure and cooled with water with a specific power of about 11 MW/cm³; therefore, the idea of using supersonic gas flows heated by plasma has a fairly good prospect.

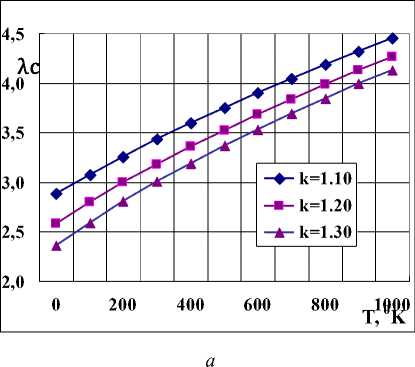
Рис. 3. Зависимость относительной скорости λ C от величины подогрева плазмой: а – до 1000 ⁰K; б – до 10000 ⁰ K

Т, 0 K

б

Fig. 3. Dependence of the relative velocity λ C on the amount of plasma heating: a – up to 1000 ⁰ K; b – up to 10000 ⁰ K

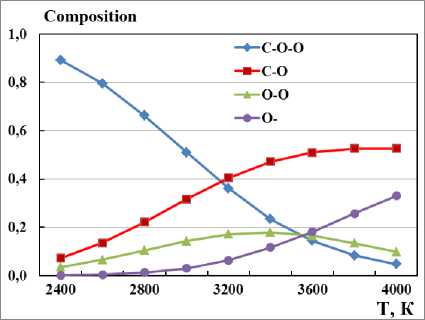
It follows from the reference data of the paper [11] that heating gases in a conical nozzle leads to partial or complete dissociation of CO 2 , H 2 O, N 2 molecules formed in the combustion chamber, which also have a higher enthalpy than inert monatomic gases: xenon, argon and helium. For example, a mixture of molecular nitrogen N 2 and radical N (the main component) at a temperature of 8000 ⁰K has heat content 5 times greater than argon. Therefore, the use of molecular gases for the formation of RF plasma makes it possible to achieve high thermal efficiency values up to 60-70% compared to ~40% for inert gases (xenon, argon and helium) [12] at high heating temperatures. The main advantage of the conical nozzle with gas heating by plasma is that the gas aready has a high initial velocity of a Cr ˃1000 m/sec and is heated above 2500 ⁰K, therefore its further heating and, accordingly, additional acceleration of molecules, atoms (ions) will be facilitated, which is one of the reasons for increasing the efficiency of this concept of an LPE. Plasma heating of the supersonic gas flow leads to the decomposition of СО 2 and Н 2 О molecules already formed in the combustion chamber into separate components, which is shown in Fig. 4 for a pressure of 0.2 MPa. The graphs are based on the tabular data [11]. Nitrogen N 2 molecules in the range up to 6000 ^оК dissociate weakly and may not be taken into account when calculating chemical reactions in plasma with a sufficiently low temperature. The exact calculation of the heating of the gas flow by plasma is complicated by the need to take into account the dependences of electrical conductivity, heat capacity, thermal conductivity and viscosity of gases at high temperature of the gas flow chemically varying along the length of the nozzle. The solution to a complex stationary system of equations of gas and electrodynamics is possible numerically using the control volume method when calculating the plasma heating zone based on MathCad programs based on [13; 14], which is beyond the scope of this work, but is described by the author in [5].

Let us specify one more direction of fuel saving. From consideration of the calculated tabular data of the work [1], we constructed a graph, shown in Fig. 5, for the proportion of unburned fuel η of a mixture of kerosene with nitric acid for pressures in two sections: critical (P1) and estimated 0.1 MPa (P2).

It can be seen from Fig. 5 that with increasing pressure in the combustion chamber, the fuel burns more efficiently and the proportion of unburned fuel decreases significantly. But even in the pressure range of РCp = 15–50 MPa, the proportion of unburned fuel in the combustion chamber is 11-13%, which, taking into account the part of the fuel going to the air heat curtain of the walls of the combustion chamber and amounting to 10-15% of its total weight, greatly reduces the full efficiency of the LPE. In addition, the cold fuel going to the air heat curtain does not mix well with the general gas flow and affects the optimal stoichiometric fuel/oxidizer ratio, reducing the Isp, including in vacuum, by 3.2–3.4%, which reduces the payload capacity of all rocket stages.

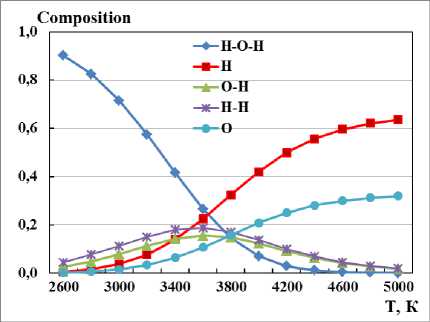
Рис. 4. Химический газовый состав атомов и молекул от температуры: а – Н 2 О; б – СО 2

б

Fig. 4. Chemical gas composition of atoms and molecules from temperature: a – H 2 O; b – CO 2

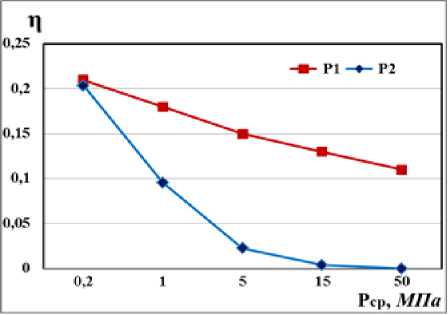
Рис. 5. Доля несгоревшего топлива η от давления в камере сгорания ЖРД Р ср

Fig. 5. The proportion of unburned fuel η from the pressure in the combustion chamber of LPE Р ср

There is no drastic solution to this problem for modern LPE designs due to the almost complete use of all possible resources: design, materials science, fuel mixtures, ballistics and rocket flight dynamics. In the new concept of constructing an LPE using plasma heating of a supersonic gas flow in a conical nozzle, the problem of unburned fuel will have a negligible effect due to the dissociation and almost complete ionization of unburned fuel residues in the gas flow heating area with low-temperature plasma and their further active participation in the additional acceleration of the entire gas flow.

Comparing the flight of the estimated models of rockets

To calculate the flight parameters of two models of rockets (proportionately reduced well-known Zenit rocket and a rocket with plasma heating of a supersonic gas flow of the Plasma type), having one LPE of small dimensions, a comparative table was made. This table takes into account all geometric and thrust characteristics (Table 1). The fuel is kerosene and nitric acid.

Таблица 1

Design parameters of models of rockets "Zenit" and "Plazma"

№	Parameter name, units of measurement	Formula	«Zenit»	«Plazma»	Remarks
1	Total thrust of an engine, N	Р E = Р 1 + Р 2	3572	7178	In a vacuum
2	Specific impulse, m/sec	W a	2736	7377
3	Section of the exit nozzle, m2	S a	0. 0145	0. 0145
4	Pressure in the combustion chamber, Mpa	Р CP	15	15
5	Maximum nozzle thrust, N	Р 1 = S a ( P CP /Ɛ C – P h )	1446	1446
6	Exhaust thrust, N	Р 2 = W a (Δ m /Δ t )	2126	5732
7	Fuel-consumption rate, kg/sec	q = (Δ m /Δ t ) = P 2 / W a	0.777	0.777	max
8	All-up-weight, kg	М с	125	150
9	Zero-fuel weight, kg	М к	50	75
10	Fuel weight, kg	m т	75	75
11	Current rocket weight, kg	m i = M ci – q ·Δ t			i = 0… n
12	Engine run time, sec	t w	100	200
13	Frontal section, m2	S F	0.0314	0.0314
14	View factor	K S	0.080	0.080
15	Air density, kg /m3	ρ = ρ о exp(–ζ· h i )			ζ ≈ 0,11 m-1
16	Mixing factor, m2	µ = K S · S F /2	0.0013	0.0013
17	Acceleration of the rocket, m/sec2	a i = [( Р E – F T )/ m i ] – g
18	Air resistance, N	F T = ρ·µ·( V) 2
19	Rocket velocity, m/sec	V i + 1 = V i + a i ·Δ t
20	Rocket flight altitude, km	h i+1 = h i + V i ·Δt
21	Air pressure, MPa	P h = P o ·exp(–γ· h i )			γ = 0,142
22	Gravitational acceleration, m/sec 2	g = g o /[( R + h i )2/ R 2]
23	Nozzle-expansion area ratio	Ɛ C	150	150	max
24	Flight time to maximum altitude, sec		420	1620
25	Engine operating height, km	H E	102	429	max
26	Flight altitude at apogee, km	H max	598	3333
27	Maximum velocity, m/sec	V max	2693	6474

Remark. R = 6378 km – Earth radius, g o = 9.809 m/sec², ρ о = 1.293 kg/m³.

The difference between the models was in the all-up-weight М с and their total thrust Р E due to different Isp caused by plasma heating of gases in a conical nozzle by ΔТ = 4000 ^оК, at a temperature in the combustion chamber equal to Т CP = 2779 ^оК. The design parameters for the flight of small-sized rocket models with a limited supply of non-cryogenic fuel were obtained using the MSExcel2010 program. The parameters corresponded to the values for Fig. 3 with the combustion chamber volume V CP = 2.6∙10^-4 m³ and cross section F Cr = 0.7854∙10^–4 m². The accuracy of the calculations for the values of mass m i ( t ), velocity V i , height H i ( t ) and total engine thrust Р ( t ) for Table. 1 was determined by the value of the time interval Δ t , which varied in the course of calculations from 1 second at the moment of launch to 20 seconds at the end of the flight. The engine thrust changed in the same way for both models - gradually increasing to the maximum value, but the fuel consumption for the Plazma model was about 3 times less, which, in fact, is typical for all models with plasma heating of the supersonic gas flow. Due to the small amount of fuel, the estimated maximum velocity did not exceed the first space velocity for mathematical models and was 2.4 times greater for the Plazma model compared to the Zenit model. For the Zenit model, the maximum velocity pressure occurred at an altitude of 11.3 km at a speed of 554 m/sec, while for the Plazma model, the maximum velocity pressure was achieved at an altitude of 10.7 km at a lower speed of 472 m/sec.

The calculation results for the Zenit (lower curve) and Plazma (upper curve) models are shown in Fig. 6 for non-uniform time scale. It can be seen that the flight altitude is much higher for the Plazma model, since its Isp is 2.7 times greater, and the full operation time of the LPE is 2 times longer, which indicates an increase in fuel efficiency with a corresponding redistribution of energy costs for ionization and plasma heating of a supersonic flow in a cone nozzle.

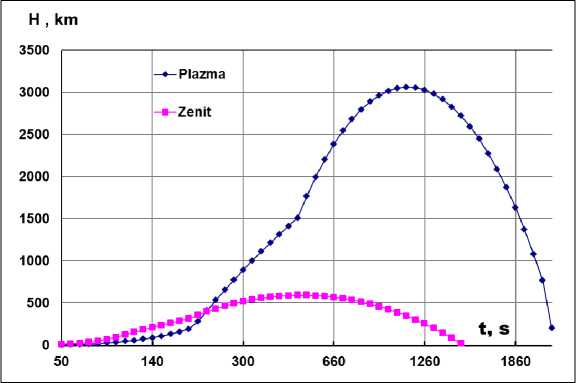
Рис. 6. Расчётная высота полёта моделей ракет типа «Плазма» и «Зенит» от времени Fig. 6. The estimated flight altitude of the “Plazma” and “Zenit” rocket models from time

The launch of the Plazma model from an aircraft at an altitude of 10 km at the commencing speed of 250 m/sec and reduced fuel reserve of 25 kg was also simulated. The calculation showed a significant improvement in all flight parameters, and the maximum attainable altitude increased, since the need to reduce speed at the moment of overcoming the velocity pressure disappeared. The maximum attainable altitude almost corresponded to the estimated flight of the rocket with the launch from the earth's surface, but heavier by 25%, which indicates the promising possibility of launching a smallsized rocket from a launch aircraft.

The estimated data for the heavier and larger models of the Plazma-17.25 and Plazma-20 rockets are presented in Table. 2, which differ in the all-up-weight, the weight of the rockets without fuel, the total thrust of the engines, the shape and expansion coefficients of the cone. The maximum estimated speeds of the rockets differ significantly: for the Plazma-20 model, the speed is greater than the second space velocity, and for the lighter Plazma-17.25 model, it exceeds the third space velocity.

Considering that the calculations were made for single-stage rockets heated by plasma of a supersonic gas flow in a conical nozzle at a temperature of Δ Т = 8000 ^оК, this result is close to the theoretical limit. A significant difference between the rocket models is the engine operation mode: for the Plazma-20 model it is economically unchanged with constant fuel consumption; and for the Plazma-17.25 model, during the first 120 seconds of operation, the thrust increases in steps, and then the engine operating condition changes twice to be more economical with lower fuel consumption. It should be noted that the heavier Plazma-20 rocket met the criterion η т = m т / М к of academician Ya. B. Zeldo-vich and equal to η т ≈ 4, therefore the achieved second space velocity was the optimal limit for calculating the given weight of the rocket.The altitude of the maximum design velocity pressure for the models is 11.4–12.25 km at velocities of 546–348 m/sec, respectively. At the end of engine operation at t = 550 sec for the Plazma-20 model, the estimated altitude is H E = 2577 km, and for the Plazma-17.25 model H E = 14046 km at t = 900 sec. The Plazma-20 model is supposed to launch a payload into geostationary orbit or beyond the Earth's orbit, and the lighter Plazma-17.25 model is intended for flights around the solar system. The graphs of speed calculations for mathematical models from the flight time are shown in Fig. 7.

Table 2

№	Parameter name, units of measurement	Formula	«Zenit»	«Plazma»	Remarks
1	Total thrust of an engine, N	Р E = Р 1 + Р 2	731220	711534	max
2	Specific impulse, m/sec	W a	8400	8400
3	Section of the exit nozzle, m2	S a	0.7854	0.7854	sum *)
4	Pressure in the combustion chamber, Mpa	Р CP	15	15
5	Maximum nozzle thrust, N	Р 1 = S a ( P СP /Ɛ C – P h )	78540	58854	sum *)
6	Exhaust thrust, N	Р 2 = W a (Δ m /Δ t )	652680	652680	sum *)
7	Fuel-consumption rate, kg/sec	q = (Δ m /Δ t ) = P 2 / W a	77.70	77.70	max
8	All-up-weight, kg	М с	17250	20000
9	Zero-fuel weight, kg	М к	1250	4000
10	Fuel weight, kg	m т	16000	16000
11	Current rocket weight, kg	m i = M сi – q ·Δ t			i = 0… n
12	Engine run time, sec	t w	550	900
13	Frontal section, m2	S F	0.9818	0.9818
14	View factor	K S	0.180	0.200
15	Air density, kg /m3	ρ = ρ о exp(–ζ· h i )			ζ ≈ 0.1 m–1
16	Mixing factor, m2	µ = K S · S л /2	0.08836	0.0982
17	Acceleration of the rocket, m/sec2	a i = [( Р E – F T )/ m i ] – g
18	Air resistance, N	F T = ρ·µ·( V) 2
19	Rocket velocity, m/sec	V i + 1 = V i + a i ·Δ t
20	Rocket flight altitude, km	h i+1 = h i + V i ·Δt
21	Air pressure, MPa	P h = P o ·exp(–γ· h i )			γ = 0.142
22	Gravitational acceleration, m/sec 2	g = g o / [( R + h i )2/ R 2]
23	Nozzle-expansion area ratio	Ɛ C	150	200	max
24	Engine operating height, km	H E	14046	2577
25	Maximum velocity, m/sec	V max	32679	13060

Design parameters of the Plazma-17.25 and Plazma-20 rocket models

*Remark. The value of the total thrust and cross section at the exit of the nozzle is presented for a bunch of many similar, small-sized engines, which is indicated by the word "sum."

With an estimated flight time of 100 minutes, the distance of the Plazma-20 model from the Earth's surface was 58413 km. At such a distance, the gravitational attraction of the earth is greatly weakened, and the gravitational acceleration to the Earth is 0.095 m/sec², i.e., it has decreased by more than 100 times with a tendency to decrease further. This means that the Plazma-20 model can carry a significant payload, for example, towards the Moon or Mars. The distance from the Earth's surface for another Plazma-17.25 model with a similar flight time was a more significant estimated value Н =178760 km, which means that the rocket can fly into intergalactic space if its trajectory is designed in a certain way.

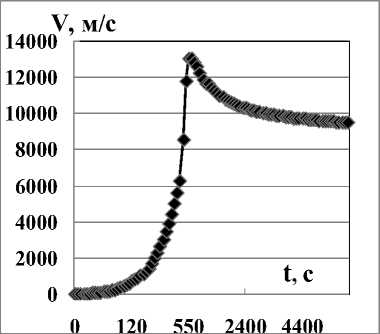
а

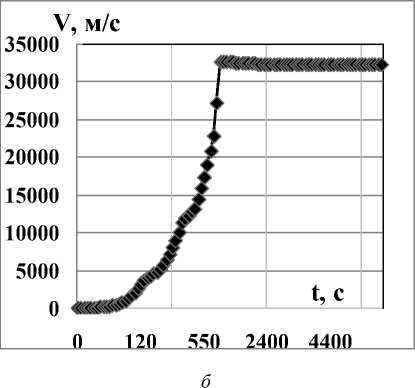
Рис. 7. Расчётная скорость полёта ракеты от времени (неравномерная шкала): а – «Плазма-20»; б – «Плазма-17,25»

Fig. 7. Estimated flight speed of the rocket from time (uneven scale): а – Plasma-20; b – Plasma-17,25

Conclusion

On the basis of the calculations performed, according to the simplified formulae proposed here, it can be assumed that the use of a significant part of fuel for generating electricity will increase the Isp by several times, which will entail a complete re-arrangement when creating a small-sized LPE heated by plasma of a supersonic gas flow in a conical nozzle. The amount of heating will be determined by the geometric dimensions of the conical nozzle, which cannot be arbitrary, but are related to the depth of penetration of the RF electromagnetic field into the plasma with optimal conductivity for maximum efficiency of the RF electromagnetic field energy transfer to the plasma flow. The heating of a supersonic gas flow by plasma in a conical nozzle differs significantly from the heating of gases in conventional RF plasmatrons due to a much larger mass of heated gases moving almost laminarly, without turbulence. Calculations of the processes occurring in the plasma of a supersonic flow can be carried out by numerical methods well developed for plasmatrons [13; 11], but taking into account the chemical reactions occurring in the zone of plasma heating. Such theoretical and experimental studies were initiated in [5] for a small water-cooled quartz reactor in the form of an LPE with a maximum short-term thermal power of not more than 4 kW, and an RF generator power for creating plasma ~1.5 kW.

The use of many small-sized, but more efficient LPEs according to the new concept for creating rockets for various purposes will probably make it possible to abandon the multi-stage concept of creating small space rockets. This trend has begun to take shape. For example, the American company Rocket Lab has created a two-stage Electron rocket with the all-up-weight of 13 tons, containing a cluster of 9 small-sized LPEs with electric turbopumps. This made it possible to successfully control the flight of the rocket without special steering engines with the prospect of reusing the first stage of the rocket with the help of a parachute, making 32 real launches in 2022 [15], lifting loads of up to 300 kg into low Earth orbits. An option of using multiple LPEs for a single engine with a central body and a variable thrust vector in flight is the Russian project of JSC Makeev State Rocket Center , which was resumed in 2017 -a single-stage Corona rocket weighing ~290 tons [16].

Further development of the idea of plasma heating of a supersonic gas flow will require practical research, elucidation of all the features of the expansion process during the dissociation of a mixture of gases: nitrogen, carbon dioxide and water. The plasma heating temperature limit is determined by the increase in optical radiation losses, which sharply increase at temperatures exceeding 6000–8000 ºK. Determining the time of ion recombination in the plasma of a gas flow as a function of temperature, which was part of the work, is very important [17]. It will also require the practical development of an ionizer for a combustion chamber with high X-ray intensity and a pulse power of up to 1 MW, the the- ory of which is given in [7]. It is necessary to study the process of ionization of a dense gas flow in the combustion chamber at pressures of 15–50 MPa and its effect on reducing the proportion of unburned fuel.

The combined method proposed in this article for a significant increase of the Isp will help reduce the cost of launching spacecraft for near and far near-Earth orbits, and, probably, start a fairly fast movement of small rockets in deep space.

Благодарности. Автор благодарит ООО «Аника М» (г. Новосибирск, за финансовую помощь при выполнении данной работы.

Acknowledgements. The author is especially grateful to “Anika M” LLC (Novosibirsk, for financial assistance in performing this work.