OpenMP Dual Population Genetic Algorithm for Solving Constrained Optimization Problems

Published Online January 2015 in MECS DOI: 10.5815/ijieeb.2015.01.08

Dual Population Genetic algorithms (DPGA) is population based search algorithm that obtains solution to optimization problems. It is a diversity based algorithm that addresses diversity as well as premature convergence problems of Genetic Algorithm (GA). DPGA uses a reserve population along with the main population. This provides additional diversity to the main population. With the existence of two populations, execution time required for evolution is further increased. Recent advancement in High Performance Computing (HPC) includes programming for multi-core processors. These processors can be employed in parallel for faster evolution of the reserve as well as the main population. Information exchange between populations takes place through interpopulation crossbreeding [1].

In this paper, Maximum Constraints Satisfaction Method (MCSM) along with DPGA to solve Constrained

Optimization Problems (COPs) are used. MCSM is a novel technique which tries to satisfy maximum constrains first and then it tries to optimize an objective function.

OpenMP is an API for writing shared-memory parallel applications in C, C++, and FORTRAN. With the release of API specifications in 1997 uses of multiple cores of multi-core CPU for parallel computing has become easy [2]. The basic execution unit of OpenMP is a thread. OpenMP is an implementation of multithreading. A master thread forks a specified number of slave threads and a task is distributed among them. The designers of OpenMP developed a set of compiler pragmas, directives, and environment variables, function calls which are platform-independent [3]. In application exactly where and how to insert threads are explicitly instructed by these constructs.

Section II gives a brief literature review of DPGA and COPs. Section III describes the proposed algorithm DPGA for solving COPs using OpenMP. Section IV presents experimental results and discussion. Section V gives some conclusions and exhibits future scope.

• II.    Literature Review

Dual Population Genetic Algorithm for solving COPs is an open research problem. Therefore we studied literature about evolution of DPGA. We have also surveyed how other Evolutionary Algorithms applied to solve COPs.

Park and Ruy (2006) [4] introduced DPGA. It has two distinct populations with different evolutionary objectives: The Prospect (main) population works like population of the regular genetic algorithm which aims to optimize the objective function. The Preserver (reserve) population serves to maintain the diversity. Park and Ruy (2007) [5] proposed DPGA-ED that is an improved design-DPGA. Unlike DPGA, the reserve population of DPGA-ED evolves by itself. Park and Ruy (2007) [6] proposed a method to dynamically set the distance between the populations using the distance between good parents. Park and Ruy (2007) [7] exhibited DPGA2 that utilizes two reserve populations. Park and Ruy (2010) [1]

experimented DPGA on various classes of problems using binary, real-valued, and order-based representations. Umbarkar and Joshi (2013) [8] compared DPGA with OpenMP GA for Multimodal Function Optimization. The results show that the performance of OpenMP GA better than SGA on the basis of execution time and speed up.

The basic and classical constrained optimization methods include penalty function method, Lagrangian method [9] and Sequential Quadratic Programming (SQP) [10]. These are local search methods which can find a local optimal solution.

Recent trend is to ensure that the use of evolutionary algorithms to solve constrained optimization problems [11,  12]. Comparing with the traditional nonlinear programming approach, evolutionary algorithms need less information such as gradient (derivatives), as well as it is a global searching approach. According to Koziel and Michalewicz [13], these algorithms can be grouped into four categories:

• i.    Methods based on preserving feasibility of solutions by transforming infeasible solutions to feasible solutions with some operators [14]

• ii.    Methods based on penalty functions which introduce a penalty term into the original objective function to penalize constraint violations in order to solve a constrained problem as an unconstrained problem [15–18]

• iii.    Methods which make a clear distinction between feasible and infeasible solutions [19–23]

• iv.    Methods based on evolutionary algorithms [24-36] v. Other hybrid methods combining evolutionary computation techniques with deterministic procedures for numerical optimization [37–40]

• III.    Proposed Algorithm

Sequential programming mostly can make use of only single core of multi-processor, which leaves other cores idle. To achieve complete resource utilization, algorithm can be built in parallel either by design or by multithreaded programming. This paper discusses the parallel implementation of DPGA using OpenMP. OpenMP maps threads onto physical cores of CPU; hence all the OpenMP threads run parallel and provide an optimal solution in less amount of time. This technique reduces execution time and provides speed up compared to sequential DPGA. The Sequential DPGA algorithm is indicated in Fig 2.

DPGA starts with two randomly generated populations viz., main population and reserve population. The individuals of each population are evaluated by their own fitness functions. The evolution of each population is obtained by inbreeding between parents from the same population, crossbreeding between parents from different populations, and survival selection among the obtained offspring [1].

The methodology for applying DPGA for COPs is described in this section. A detailed pseudo code is explained in Fig.2 entitled DPGA_MCSM. MCSM is a novel technique based on Deb’s rule that in the category of methods searching for feasible solutions. It states any feasible solution is better than any infeasible one [23]. According to the first phase of MCSM, Pseudo Random Number Generator (PRNG) selects variables to prepare individuals which satisfy all constraints. According to the second phase of MCSM, meta-heuristic DPGA is applied for evolution of both populations via inbreeding. After crossbreeding of individuals from both populations, DPGA evolves till stopping criteria are met.

The objective function is used as fitness function for evolution of the main population. Fitness function for the reserve population is defined in another way. An individual in the reserve population is given a high fitness value if its average distance from each of the individuals of the main population is large. Therefore the reserve population can provide the main population with additional diversity.

Equation (1) describes fitness function for reserve population. Each individual of the reserve population can maintain a given distance δ from the individuals of the main population [1, 4, 5].

frδ(x)=1-|δ-d(M,x) | (1)

Where,

d(M, x) : average distance (0 ≤ d(M, x) ≤ 1) between the main population M and individual x of the reserve population

δ : desired distance (0 ≤ δ ≤ 1) between two population

The OpenMP DPGA algorithm exactly emulates the sequential algorithm stated in Fig.2 except for fitness calculation function, wherein small changes are introduced to get better performance.

This method evaluates fitness of each individual using a defined objective function. As fitness evaluation of each individual is an independent step it can be executed in parallel. OpenMP parallel directives are used to create multiple threads, ranging from 2 to 16. These threads to evaluate each individual’s fitness separately. In this way, this step reduces the overall time required to evaluate the fitness of all individuals in the population. Thus it helps to reduce the amount of time required for total execution significantly.

• IV.    Experimental Results and discussion

  The results are taken on AMD FX(tm)-8320 EightCore processor which is of 3.51 GHz clock speed. The machine is equipped with 16 GB RAM and hard disk of capacity 500 GB. Operating system used is CentOS Release 6.5 with Kernel Linux 2.6.32-431.6l6.x86_64 and GNOME version 2.28.2. The IDE used is Eclipse-CDT with gcc compiler.

We take standard problems to conduct experiments from Problem Definitions and Evaluation Criteria for the

Congress on Evolutionary Computation 2006 Special Session on Constrained Real-Parameter Optimization problem [41]. In this report, 24 benchmark functions are described. Guidelines for conducting experiments, statistical parameters and its formulae, performance evaluation criteria are given at the end of this report.

Table 1. Function Description

Function	D	Type	LI	NI	LE	NE
g01	13	Quadratic	9	0	0	0
g04	5	Quadratic	0	6	0	0
g06	2	Cubic	0	2	0	0
g08	2	Nonlinear	0	2	0	0
g09	7	Polynomial	0	4	0	0
g10	8	Linear	3	3	0	0
g18	9	Quadratic	0	13	0	0
g24	2	Linear	0	2	0	0

Table I describes 8 functions from CEC 2006 that we have implemented using DPGA_MCSM. It describes function name, dimension (D), the type of function, no. of linear inequality constraints (LI), no. of non-linear inequality constraints (NI), no. of linear equality constraints (LE) and no. of non-linear equality constraints (NE).

Table 2. Parameter Settings

Crossover Rate	0.80	Elitism Rate	0.10
Mutation Rate	0.09	Crossbreed Rate	0.10
Main Pop. Size	1000	Reserve Pop. Size	1000

Table II describes the parameter settings used for experimentation. All 8 functions use parameter values from Table II. Consecutive 30 runs are calculated for each function keeping these parameter values constant. Size of the main population as well as the reserve population is taken as 1000. Crossover rate, elitism rate, mutation rate and crossbreed rate are kept identical for both the main population and the reserve population.

The performance of OpenMP DPGA is checked based on the quality of solution found and speed up given by DPGA as compare to the Sequential DPGA.

• 1)    Convergence of Proposed OpenMP DPGA

Algorithms

Proposed parallel algorithm gives a solution of problems close to the optimal solution obtained as a result of the sequential algorithm. Table III shows Optimal Solutions Found (OSF) in sequential as well as OpenMP DPGA algorithm. For OpenMP DPGA, the results are taken on 2, 4, 8 and 16 cores. Results show that, OpenMP DPGA algorithm converges and produces the same and sometimes better solution as that of the Sequential DPGA algorithm.

• 2)    Increase in Number of Cores

OpenMP DPGA for COPs using MCSM experimented on different multi-core machines. Table II gives the speed-up using 2, 4, 8 and 16 cores machine for the test problems.

Speed-up measures performance gain is achieved by parallelizing a given application over sequential implementation. The speed-up is the ratio of sequential run time to parallel run time (equation 2).

Table 3. OSF in Sequential, OpenMP DPGA

Function	Sequential DPGA OSF	OSF in OpenMP DPGA
		2 Cores	4 Cores	8 Cores	16 Cores
g01	-10.87	-10.87	-11.00	-10.88	-10.70
g04	-30490.1	-30500.2	30288.3	30478.4	30145.2
g06	-6691.47	-6690.47	6790.47	6680.47	6614.47
g08	-0.08918	-0.09200	0.08888	0.08718	0.08874
g09	663.23	662.14	663.47	661.14	660.78
g10	5876.11	5877.11	5886.22	5864.47	5861.33
g18	-0.75926	-0.74426	0.72614	-0.72476	0.74696
g24	-5.43	-5.44	-5.43	-5.42	-5.41

S = ^{T s}                    (2)

Tp

The results of speed-up obtained on 2, 4, 8, 16 cores machines by OpenMP DPGA for 8 test functions of CEC 2006 are shown in Table IV.

Table 4. Speed ups obtained by OpenMP DPGA on 2-16 cores system

Function	Speed Up by OpenMP DPGA
	2 Cores	4 Cores	8 Cores	16 Cores
g01	1.97	2.12	2.15	2.10
g04	4.40	4.40	4.40	4.40
g06	1.40	1.60	1.40	1.40
g08	0.90	1.00	1.00	1.00
g09	1.00	1.00	1.00	1.00
g10	1.00	1.00	1.00	1.00
g18	1.00	1.10	1.10	1.10
g24	1.00	1.10	1.10	1.10

It is observed that, as the number of cores increases, speed-up increases and it remains constant limited by sequential part of the code. The corresponding graph in Fig.1 shows the speedup for the average of the same 8 test functions.

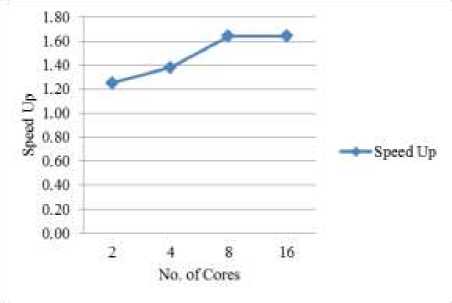
Fig.1. Speedup versus number of cores

In the above experiment, keeping problem size (population size) constant, no. of cores (processors) are increased in multiples of 2. From literature, the overhead time is time required for creating threads and some other initialization and maintenance tasks. It is formulated as

To = pTp - Ts (3)

Where, To is overhead time, Tp is parallel run time required for p processors and Ts is part of code that cannot be parallelized. The overhead time is function of the increment in no. of processors. As Amdahl’s Law says this increased To limits speed up and efficiency and is demonstrated in Table V.

V. Conclusion

OpenMP DPGA is a novel technique for solving COPs. Its aim is to use all available cores of current age multicore processors. Experiments conducted using CEC 2006 problems set show increase in speed up with increase in no. of processors till certain no. of processors and then speed up remains constant. This behavior emulates Amdahl’s Law.

In future, using alternative constraints handling method, parallel algorithm and high performance computing paradigm a better speed up can be achieved.

APPENDIX A.

g01: Minimize

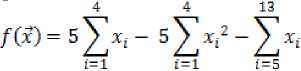
Subject to
gt (x) = 2x7 + 2x2 + 2x10 + 2xn — 10	< 0
gt (x) = 2x7 + 2x2 + 2x10 + 2xn — 10	< 0
y2 ® = 2x7 + 2x3 + 2x10 + 2x12 — 10	< 0
Уз ® = 2x2 + 2x3 + 2xn + 2x12 — 10	< 0

У4® = -8x1 + x10< 0

Уз® = -8х₂+х_и < 0

Уб® = -8x₃ + x₁₂ < 0 y₇(x) = 2x₄-x₅+x₁₀< 0

Ув® = 2х₆-х₇+х_п< 0

y9(x) = 2xg — x9 +x12 < 0

where the bounds are 0 <= xi <= 1 (i=1,……,9), 0 <= xi <= 100 (i = 10, 11, 12) and 0 <= x13<=1 .

g04: Minimize

Дх) = 5.3578547x3 + 0.8356891XJ + Xs + 37.293239хг

-40792.141      "              "    "              "

Subject to y2® = 85.334407 + 0.0056858x2x5 + 0.0006262x^4

+ 0.0022053x3xs - 92 < 0

y2® = _85.-334407Х! - 0.0056858x2x5

—0.0006262x1x4 + 0.0022053x3xs < 0

Уз® = 80.51249 + 0.0071317x₂X₅+ 0.0029955x₁X₂

—0.0021813x3 - 110 < 0

дЛх) = -80.51249 - 0.0071317x₂x₅ - 0.0029955x,x₂

—0.0021813x3 + 90 < 0          "                " "

y5® = 9.300961 + 0.0047026x3xs + 0.0012547x1x3 + 0.0019085x3x4 - 25 < 0

g₆U) = -9.300961 - 0.0047026x₃x₅ - 0.0012547x₁x₃

—0.0019085x₃x₄ + 20 < 0

where 78 <= x 1 <= 102, 33 <= x 2 <= 45 and 27 <= x i <= 45

(i = 3, 4, 5).

g06: Minimize

/® = (xi- 10)3 4 (x2 - 20)3

Subject to

51® = -(X! - 5)² - (x₂ - 5)² + 100 < 0 g^x) = (x₂ - 6)² + (x₂ - 5)² - 82.81 < 0 where 13 <= x1<= 100 and 0 <= x2<= 100.

g07: Minimize f ® = x? + x2 + xnx2 — 14xi — 16x2 + (x, — 10)2 +4(x4 - 5)2 + (x5 - 3)2 + 2(x6 — I)2 + 5x2 +7(x8 - 11) 2 + 2(x9 - 10)2 + (x10 - 7)2 + 45

Subject to gT (x) = —105 + 4xt + 5x2 — 3x7 + 9x8 < 0

y₂ ® = 10x_t — 8x₂ — 17x₇ + 2x₈< 0

Уз ® ⁼ —8x_t + 2x₂ + 5x₉ — 2x₁₀ —12 < 0 y₄® = 3(x_x - 2)² + 4(x₂ - 3)² + 2xj - 7x₄ - 120 < 0 y₅® = 5x² + 8x₂ + (x₃ — 6)² — 2x₄ — 40 < 0

Уб® = *i + 2(x₂ — 2)² — 2х_гх_г + 14x_s — 6x₆< 0 y₇® = 0.5(х_г — 8)² + 2(x₂ — 4)² + ЗХ5 — x₆ — 30 < 0 Ув® ⁼ —3x_t + 6x₂ + 12(x₉ — 8)² — 7x₁₀< 0 where -10 <= xi<= 10 (i = 1,…., 10).

g08: Minimize sin3(27rx1)sin(27rx2)

fw =--57—,—;--

X^X! + X2)

Subject to g^x) = x® x2 + l<0

5₂(x) = I - x_t + (x₂ - 4)²< 0

where 0 <= x1<=10 and 0 <= x2<= 10.

g09: Minimize

f(x) = (xj - 10)² + 5(x₂ - 12)² + x^ + 3(x₄ - ll)²

4-X; — 4x₆x₇ — 10x₆ — 8x₇

Subject to y7® = -127 + 2x2 + 3x2 + X3 + 4x| + 5xs < 0 g2 (x) = -282 + 7хг + 3x2 + 10x3 + x4 - x5 < О

Уз® = -196 + 23x₇ + x² + 6xf — 8x₇ < 0

04(x) = 4xf + х2 — Зхгх2 + 2xj + 5х6 — 11х7 < О [6]

where- 10 <= xi<= 10 for (i = 1,….., 7).

g10: Minimize

7(х) = х1 + х2 + х3

Subject to

01 (х) = — 1 + 0.0025(х₄ + х₆) < О

02(х) = -1 + 0.0025 (х5 + х7 - х4) < О

5з(х) = -1 + 0.01(х8 — х5) < О

0»(х) = -х_тх₆ + 833.33252х₄ + 100х_х - 83333.333

05(х) = —Х₂Х₇ + 12Б0х₅ + х₂х₄ — 1250х₄ < О

0₆(х) = -х₃х₈ + 1250000 + х₃х₅ - 2500х₅ < О where 100 <= x 1 <= 10000, 1000 <= x i <= 10000 (i = 2,3)

and 10 <= x i <= 1000 (i = 4,…,8).

g18: Minimize

= _ о ₅ f^xi ^х4 - х₂ х₃ + х₃ х₉ - \ ' ^J      ■ X Хч Xq + Хч Xr — ХьХт )

Subject to ggl (х) = х2 + х2 — 1 < 0

55б(х) = (xi - х? )2 + (х2 - х8)2 - 1 <0

557 (Л) = (х3 - х5)2 + (х4 - хьУ - 1 <0

55а (Л) = (х3 - х7)2 + (х4 - х8)2 - 1 <0

ggs (х) = х2 + (х8 - xs )2 - 1 <0

55ю (5) = х2 х3 - хт х4 < 0

5511 (Л) = -х3х9 < 0

5512 (х) = х5 х9 < 0

5513 (х) = х6х7 - х5хв < 0

where the bounds are - 10 ≤ xi ≤ 10 ( i = 1 , . . . , 8) and 0 ≤ x 9 ≤ 20.

g24: Minimize

7(х) = -хг-х2

Subject to

0з(х) = —2х^ + 8Xi ~ ^^xi + х₂ — 2 < О                  [15]

02 (х) = -4xJ + 32xf - 88xf + 96хг + х2 - 36 < О where the bounds are 0 <= x1<= 3 and 0 <= x2<= 4.

Acknowledgment

We express our sincere thanks to all authors, whose papers in the area of evolutionary algorithm/DPGA and COPs is published in various conference proceedings and journals. Our special thanks to T. Park, R. Choe and K.R. Ryu for their work on Dual Population Genetic Algorithm published in various journals and conferences.