Operation optimization strategy of multi-microgrids energy sharing based on asymmetric Nash bargaining

Бюллетень науки и практики / Bulletin of Science and Practice

UDC 621.31                                       

With the high concern of the global energy crisis, renewable energy generation such as wind energy and PV has been widely used [1, 2]. However, with the increasing installed capacity and penetration of renewable energy, the stable operation of power system is challenged and causes a large proportion of abandoned wind and light, and energy storage is one of the best ways to solve the problem of renewable energy consumption [3, 4].

With the development of distributed energy storage, the economic model of shared energy storage is receiving more and more attention. A market-based consumption model based on “shared energy storage and demand side resources” has been proposed in the literature [5], which can promote the accommodated of renewable energy through the analysis of calculation cases. The literature [6, 7] studied the optimal allocation of shared energy storage, and by optimizing the capacity and charging and discharging strategies of shared energy storage, the utilization of energy storage resources can be improved. In order to reduce the energy costs of user groups, a collaborative optimization model for integrated energy systems with the objective of economic optimization of user groups was developed in the literature [8]. To analyze the impact of transmission cost and network loss on the game outcome, a shared energy storage planning model on the generation side was proposed in the literature [9]. In the literature [10], a two-layer optimization model for shared energy storage configuration in industrial parks was solved using a robust optimization algorithm. In the literature [11], a capacity optimization allocation model for shared energy storage systems under multi-regional integrated energy system interconnection is proposed, and the calculation example shows that it can reduce the system operation cost and optimize the shared energy storage system parameters. The literature [12] proposed a service model of shared energy storage power plant in a multi-micro-energy network to highlight the superiority of shared energy storage by comparing the scenarios without and with separate energy storage configuration. The literature [13] analyzed the practical benefits of using shared energy storage in residential communities.

Shared energy storage involves optimal scheduling among multiple control subjects, while in reality, power stations, energy storage plants and various user subjects are different interest subjects, with no information interaction between them, all aiming at maximizing their own interests, which will cause disorderly competition and reduce the efficiency of the market. Therefore, cooperative and non-cooperative game theories are often used to solve the problem of benefit distribution among multiple subjects [14]. Noncooperative games refer to how multiple subjects make decisions to

Бюллетень науки и практики / Bulletin of Science and Practice Т. 8. №8. 2022 maximize their own interests in the process of interacting interests, emphasizing individual rationality [15]. For example, the literature [16] proposed an integrated energy optimal dispatch model with the objective of minimizing the cost of each energy system using noncooperative game theory. In contrast, cooperative games emphasize group rationality, taking into account both individual and overall interests. Nash bargaining theory belongs to the category of cooperative games and is used to solve the problem of equilibrium distribution of benefits among multiple subjects. In the literature [17], a Nash bargaining cooperative optimization model for a scenic hydrogen multi-body energy system was proposed and solved using alternating direction method of multipliers (alternating direction method of multipliers ADMM). The literature [18-20] describes a multi-microgrid power trading model based on Nash bargaining theory. The literature [21] proposes an integrated energy trading model based on Nash bargaining considering the uncertainty of market prices, renewable energy and integrated demand response. A Nash bargaining based energy trading market was designed in the literature [22].

With the development of multi-agent system technology, distributed optimization provides new ideas for optimal scheduling of shared energy storage. As an important method in the field of distributed optimization, the alternating direction multiplier method combines the decomposability of the pairwise ascent method and the upper bound convergence property of the multiplier method to obtain the solution of the original problem by solving each decomposition subproblem alternately. In this regard, the literature [23] proposed a distributed optimal dispatch model for a joint interconnected shared energy storage system using ADMM; literature [24] proposed an ADMM-based distributed scheduling method for off-grid interconnected shared energy storage combined systems; The literature [25] implements subarea optimization of shared energy storage plants based on ADMM. The distributed algorithm used in the above papers [26-28] can make up for the shortcomings of centralized optimization, avoiding the transmission of large amounts of data, while protecting the operational privacy of shared energy storage plants. Therefore, in this paper, the proposed model is solved in a distributed manner using ADMM.

In this paper, we will study the multi-subject cooperation model for shared energy storage plants and industrial user groups and analyze the main benefits of the whole system. Firstly, we establish the joint operation model of the campus shared energy storage plant (park energy storage ， PES) and industrial users, and then establish their cooperative operation Nash bargaining model, and transform this nonlinear problem into 2 sub-problems of the whole system revenue maximization and electric energy transaction payment bargaining. Finally, the distributed solution of these two subproblems is achieved sequentially by the alternating direction multiplier method, and its validity is demonstrated by relevant arithmetic examples.

A virtual schematic of a typical shared energy storage plant is shown in Figure. In the traditional multi-body operation mode, most of them adopt the form of “self-generation, surplus power online”, while the enterprises in the industrial park purchase power from the grid at industrial tariffs to meet the load demand of industrial users. The shared energy storage power plant, on the other hand, can provide shared services to many users in a park or in the same distribution area, i.e., users can charge and discharge their demand without time and capacity constraints [23]. Depending on the amount of charging and discharging by the user using the shared energy storage plant, the user needs to pay the corresponding fee to the shared energy storage plant.

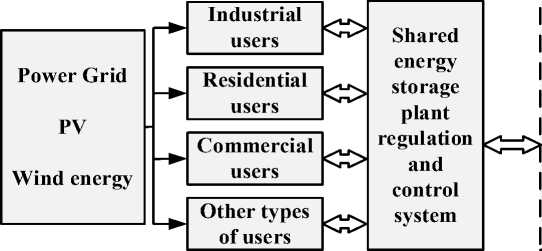
Large-scale customer-side Shared energy storage plants

Figure 1. Virtual schematic diagram of shared energy-storage power station

The transaction objects of shared energy storage plants include external power grids and various industrial user entities, and their operating costs include the charging and discharging costs of energy storage equipment c^ , interaction costs with the external grid Ctrl and the cost of interaction with the user Cpu . Sharing the benefits of energy storage plants t^PES can be expressed as the opposite of the total operating cost, that is, the benefit maximization operation model of PES:

max[/PES — (C* + (7^1 + Cpu)(1)

^e=£[PA(«)+M)]^(2)

i = l

Gri=-^/шы*)(3)

c.^-^^Q^sM(4)

where: 7' is the scheduling period; N is the number of industrial users; P^t) is the charging amount of the energy storage device in the t period; PiJt") is the discharge amount of the energy storage device in the t period; т is operation and maintenance cost factor for energy storage equipment; Ps (t) is the amount of electricity sold from the shared energy storage plant to the external grid in time period t ; ?(C is the price of electricity sold to the grid; Q^.i (i) is the interactive power between the shared energy storage power station and industrial user i (less than 0 means buying electricity from users, and greater than 0 means selling electricity to users); S,(t) is the interactive electricity price between user i and the shared energy storage power station.

Ignoring equipment losses, the operating model of a shared energy storage power station should meet the following constraints:

• 1)    Electric power balance constraints of shared energy storage power stations in the park

P^t) — P_diB(t) + P_s(t) + Q_c,,(t) = 0

• 2)    The upper and lower limits of charge and discharge of energy storage

0^

^h(i)

Pdis(£)

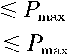
0^

Бюллетень науки и практики / Bulletin of Science and Practice Т. 8. №8. 2022 where: -^max is the maximum charge/discharge power of the shared energy storage plant

• 3)    Non-negativity constraint on transaction volume with external grid

Fs(*) ^0

• 4)    Continuity Constraints on State of Charge of Shared Energy Storage Power Stations

SSOCmin ^ 5soc (t) ^ SSOCmax a       _ a              ^ch-^ch(^) ?7disPlisO)

^SOC^J “^SOC^             p where: Ssoc(t) is the state of charge of the shared energy storage power station at time ; SSOCmax 、 'S'sOCmin are the upper and lower limits of the state of charge of the shared energy storage power station, respectively; ^max is the maximum capacity of the energy storage plant; ^ch 、 ^dis are the charging and discharging efficiencies of the shared energy storage power station, respectively.

The main industrial user considers the demand response of the load, adjusts the power consumption plan, determines the interactive power between the energy storage power station shared with the external power grid and the park, and aims to minimize the operating cost. Its operating costs include the un-comfortable cost of electric load adjustment Csl , the interaction cost with external power grids Ctr2 and the interaction cost with shared energy storage power stations C*p_U . Then the benefit Ui maximization model of industrial user main body i is:

maxUi = - (Csl + Ctr2 + C'u)(10)

csl = C1|ptu^l + dPeUtG)l(11)

4=14=1

where: Лгап(0 is the amount of adjustable electrical load in time period t ; Ли1(^) is the amount of electrical load that can be cut in time period t ; Cl 、 c-> are the compensation costs per unit of adjustable load and curtailable load, respectively; ^CTOU (^) is the industrial time-of-use tariff; Pb(t) is the amount of electricity purchased by the customer from the external grid; p?,i(t) is the amount of electricity that user i interacts with the shared storage plant in time period t (greater than 0 for selling electricity to the PES and less than 0 for buying electricity from the PES).

Ignoring equipment loss, the constraints that the operating model of the industrial user body should satisfy are as follows:

• 1)    User's Electric Load Power Balance Constraint

L_e(t) = Z_e0(i) + P_traii(^) + Pcut(^)                               (14)

where: ico(^) is the customer's electrical load;M*) is the actual electrical load of the customer after demand response.

• 2)    User's curtailable power upper and lower limit constraints

where: -^cut, max is the maximum allowable load shedding for the system..

• 3)    User-adjustable upper and lower limits of electrical power

|Лгап (^I^AG^eO^)

T

^Piian(t)=0

i = 1

where: f_s(t) is the proportion of the electricity load that the system allows to adjust to the total electricity load in the t period.

• 4)    Non-negativity constraint on transaction volume with external grid

ps(t)^o

PM^o

• 5)    User's Electric Power Balance Constraints

Left) Pbft) P Psft) + Pe,ift) PpftftP®                        (18)

where: Ppv(t ) is the PV output value for t period.

The research shows that the solar irradiance approximately obeys the Beta distribution, and the photovoltaic output power -Ppv has a linear relationship with the solar irradiance [29, 30]. Therefore, the probability density function of -fpV can be represented as [31]:

fp(Ppy) —

гы + гы Г(д1)Г(д2)

PpN Pw,max

where: -PpV,max is the maximum value of -Ppv ; Z^i and М2 are shape factors, taken as 3 and 5, respectively; is a Gramma function.

In order to reduce the influence of uncertainty on system operation, this paper adopts the processing method of literature [31]: the mathematical expectations F-PV of p(Fp_v) in each time period are used as reference values. More details can be found in [31].

At present, the commonly used cooperative game methods in the power industry include Shaply score method, Stackelberg game, Nash bargaining, etc. The Shaply score method ignores the interaction between the participants. The actions of the participants in the Stackelberg game have a sequence of actions, which are not in line with the purpose of this paper. Research. The Nash bargaining theory can help distributed decision makers achieve fair distribution of resources and Pareto optimal benefits [30]. At the same time, for subjects with potential for cooperation but conflict of interests, Nash bargaining can effectively make each subject coordinate with each other.

This paper assumes that the shared energy storage power station in the park and each industrial user belong to different stakeholders, and each subject seeks to reach a consensus on the transaction, and to determine the power and price of electricity trading fairly and reasonably, so as to maximize the individual and overall benefits. A standard Nash bargaining problem can be expressed as:

N maxJ]([Z_n-[/“) n = 1

s.t. Un^U° where: N is the number of subjects participating in the bargaining; U„ is the income after subject n participates in the bargaining and cooperation; u n is the breaking point of the bargaining, that is, the profit before the entity n participates in the bargaining and cooperation.

In order to incentivize mutual coordination among the agents, the feasible set of Nash bargaining only includes better gains than the bargaining breaking point. The model formula (20) can be further equivalently transformed into:

max

s.t. U_n^U°

Applying the Nash bargaining theory to the cooperation between the shared energy storage power station in the park and various industrial users in this paper, the following basic model can be obtained:

N max(/7PES — Upes) ]^[(Ц, — U^' ) i=i

• s.t. Upes ^ Upes

Ui ^ U°*

where: Uppe, 、 и I* are the maximum benefits of shared energy storage power stations and industrial users when they do not participate in the cooperation and are constants.

Model (22) is essentially a non-convex nonlinear optimization problem. If the model is equivalently transformed and transformed into the sub-problems of system revenue maximization and power transaction payment bargaining, the difficulty of solving will be greatly reduced.

According to the inequality of the mean

/ax + Яг + —h am \ ™

Available, to make equation (22) take the maximum value, satisfy o/pES-tra+^(^-cAo;)

Take the maximum. Make:

{t^i — - (Cd + C_tr2) |      “ (^de + Grl)

From formula (4) and formula (13), we can get            ,then max([/PES + U,) О max^ + wp)                        (26)

Subproblem 1: System revenue maximization problem

max (u, + ca_p)

s.t. Pe/t) +Qe^{t) =0

Eq.(25), (2). (3). (5)-(9)

Eq.(ll), (12), (14)-(18)

Subproblem 2: Power transaction payment bargaining problem

min

ln(a>;-(7pu-^s) + 1п(са*-С;и-[/"’*)

s.t. q(t) ^6_г(Р) ^c_TOU(t) ^-c^-Ks^o ^-^-[/Г^О Eq.(4), (13)

where: w_P 、 ^^ is the optimal solution to subproblem 1.

From the above model and analysis, it can be obtained that equation (27) solves the maximum value of the total revenue of the main body of the shared energy storage plant and the industrial user in the park, but the interaction costs and between the shared energy storage plant and the industrial user cancel each other in the solving process, so it is impossible to solve the amount of electricity traded by each body individually, which is the importance of introducing Nash bargaining theory. By solving subproblem 2, we can find the electricity trading price and determine the amount of electricity traded by each entity.

In this paper, we will use ADMM and call the commercial solver CPLEX and the optimization solver MOSEK in MATLAB 2020b and the YALMIP toolbox for the distributed solution of the 2 subproblems.

ADMM can protect the privacy of each subject during bargaining, but also has the advantages of fast processing speed and good convergence performance. ADMM is mainly used for solving convex optimization problems with constraints [31].

пйп[/(^ж) +Hz)] s.t. Ax + Bz = c

where: x, z 、 are optimization variables: A, B, c are correlation matrices. The corresponding augmented Lagrangian function can be expressed as:

L(x,z,X)=f(x) + g(z) + Ат(Аж + Bz — c) + ^\Ax + Bz — c\2

Бюллетень науки и практики / Bulletin of Science and Practice Т. 8. №8. 2022 where: л is a Lagrangian multiplier; р is the penalty factor.

When PM+QM=O is satisfied, it indicates that the power expected to be sold by the shared energy storage plant to the industrial user is the same as the power expected to be purchased by the industrial user from the shared energy storage plant, and both parties reach a consensus on the transaction. To solve this problem, the Lagrange multiplier А^г , penalty factor р* and convergence accuracy £ are first introduced, then the distributed optimal operation model of shared energy storage plant and industrial user body can be obtained.

• 1.    Shared energy storage plant distributed optimal operation model

• 2.    Industrial user body distributed optimization operation model

Cde + Gil +        '

. 1^1>ЧЛ,(*)+<Ы*)] +

s.t. Eq.(5)-(9)

' Csi + Ctr2 +         '

. l£A4PUi)+QUi)] +

Ey lin..(i)+Q_e,_!(i)lll

^s.t. Eq.(14)-(18)

The distributed algorithm for the system revenue maximization problem is then established according to the distributed iterative model, with the iterative formulation:

F+1 = r + /[P^(t)+QeT(i)]                      (33)

The iteration is carried out by equation (33), and the iteration stops when the convergence condition of equation (34) is satisfied, completing the solution of the system revenue maximization problem.

The desired interaction power between the shared energy storage plant and each industrial user body Qe.i (t) and PZ.W can be obtained by solving the subproblem 1, and then the interaction cost between them can be expressed as:

i=l t=l T c^ = ~Yy^6^

To solve subproblem 2, Lagrange multipliers X and penalty factors 'ф are introduced. in addition, auxiliary variables3 must be introduced to decouple the interaction tariffs. An auxiliary variable hi must also be introduced to decouple the interaction tariff. Si(t) can represent the interaction tariff expected by the shared energy storage plant, then can be understood as the interaction tariff expected by the industrial user body.

ш=6^)

Substituting equations (35) and (36) into the model equation (28), a distributed optimization model of power trading prices for shared energy storage plants and industrial user subjects is obtained.

1) Distributed optimization model for power trading price of shared power storage plants

_ln Ч+ЕЕ^ЖМ +

. J NT

mm EEE^w.(c]+EE^IIw-woll

V 4=1 /=1

s.t. w* + ^^QL^S^-Up^^O

4 = 1 e=l

2) Distributed Optimization Model of Power Trading Price for Industrial User Subjects

_ln ^’+Ep-w^) + min Е4ад-ад]+

E^lwo-Mi:

s.t. ^+^p:jf)k.(t)-ur^o

The distributed algorithm for the system revenue maximization problem is then built according to the distributed iterative model, and the iterative formulation is:

x^+i = x^. + ^i(t)_^^

max

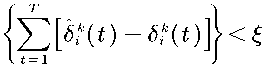
The iteration is carried out by equation (39), and the iteration stops when the convergence condition of equation (40) is satisfied, completing the solution of the electricity transaction payment bargaining problem. The ADMM algorithm flow is shown in Figure.

Figure

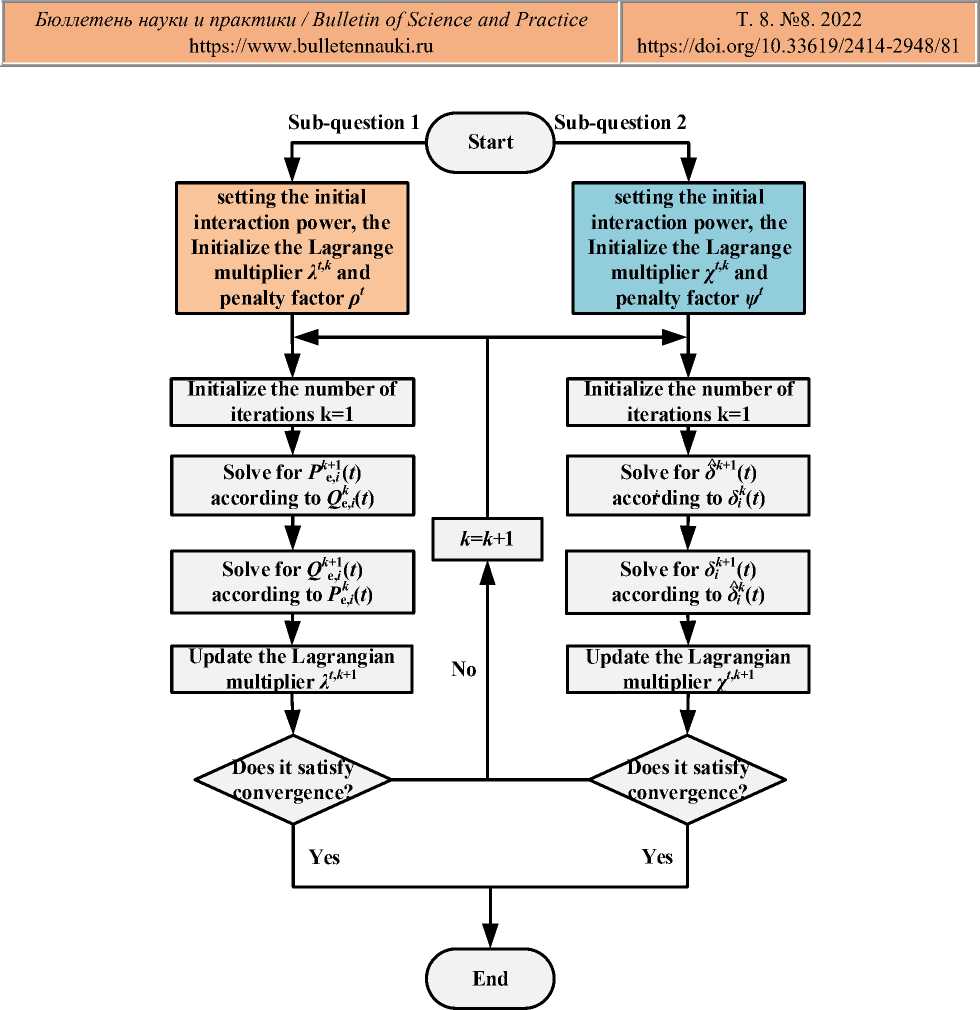
Figure 2. Flow chart of ADMM algorithm solving

In this paper, MATLAB2020b software is applied to simulate the case, and the simulation data are compared and analyzed to verify the superiority and effectiveness of the proposed model and algorithm.

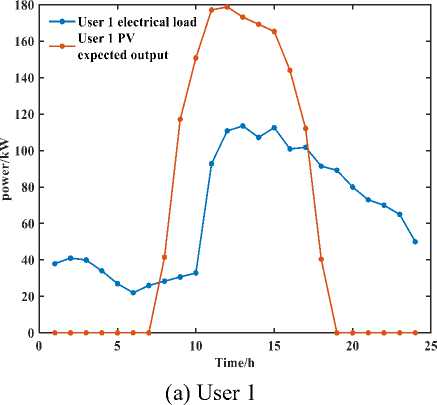
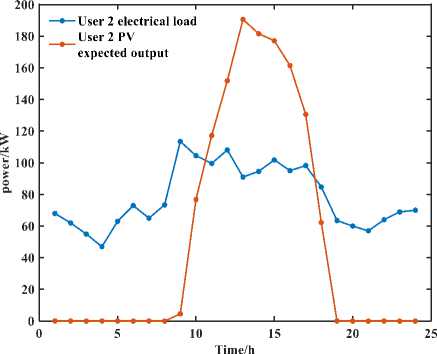
For the example, three typical industrial users are selected, user 1 is a food manufacturing plant, user 2 is a textile and garment manufacturing plant, and user 3 is a furniture manufacturing plant, and their electrical load curves and PV output curves are shown in Figure. The maximum and minimum charge states of the shared energy storage plant are taken as 0.9 and 0.1, respectively, and the initial charge state is 0.2 with a maximum capacity of 500 kW-h. The maximum charge/discharge power for users using the shared energy storage plant is 185kW. The maximum curtailable load allowed by the system is 0.10 of the total electrical loads, and the adjustable load is 0.15 of the total electrical loads.

	Table 1 ELECTRICITY PRICE
Time period type	Time period              Electricity price /($·(kW·h)-1)
Peak	11:00–14:00                         1.20 18:00–22:00
Ping	07:00–11:00                         0.75 14:00–18:00
Valley	22:00–07:00                         0.40

(b) User 2

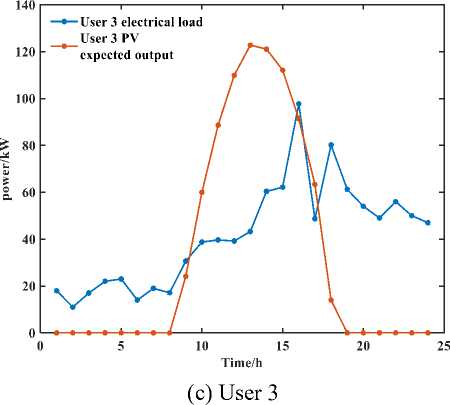
Figure 3. Curves of user electric load and photovoltaic output

The interaction power between the shared power storage plant and each user body is shown in Figure. The results of power trading for each subject are shown in Figure 7. The charging and discharging power and power status of the shared power storage plant are shown in Figure.

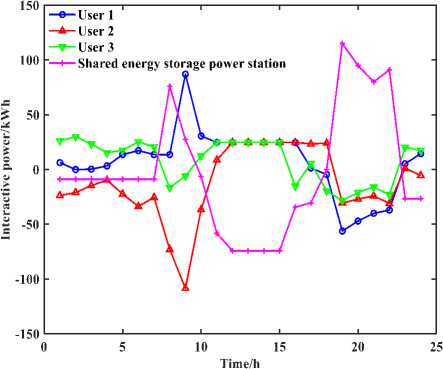
Figure 4. Interactive electricity between

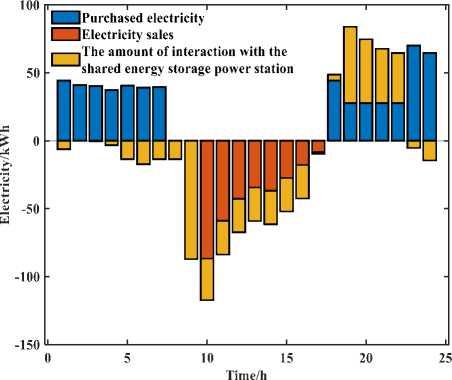
Figure 5. Electricity transaction results of user

shared energy-storage power station and users       1

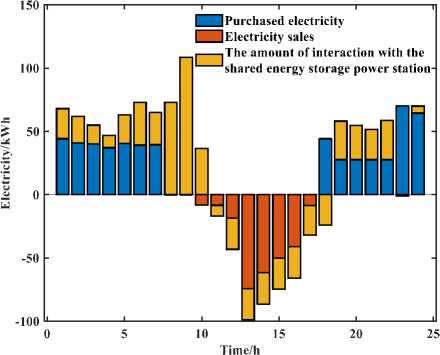
Figure 6. Electricity transaction results of user 2

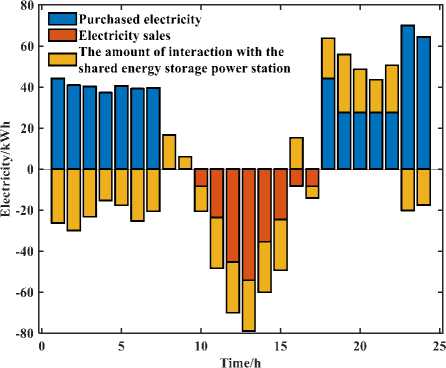
Figure 7. Electricity transaction results of user 3

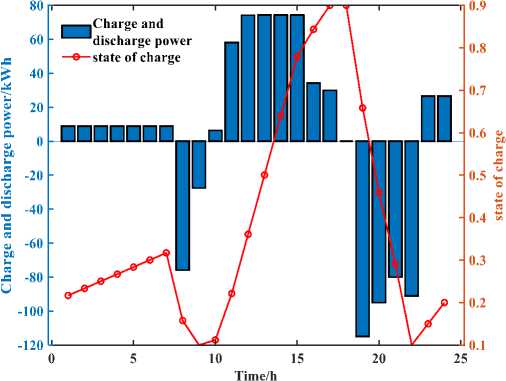
Figure 8. Charging/discharging power and electricity state of shared energy-storage power station

Бюллетень науки и практики / Bulletin of Science and Practice Т. 8. №8. 2022

From Figure (a) and Figure 5, it can be seen that during the hours 00:00–07:00 and 17:00– 24:00, as the PV output is less than the electric load power of the users, the users’ electricity demand cannot be guaranteed, and User 1 meets the load demand by sharing the discharge of the storage plant and purchasing electricity from the external grid. During the period 07:00–17:00, the PV output is greater than the user’s load demand. At this stage, the user stores the remaining power through the shared storage power station to avoid the phenomenon of abandonment and considering the maximum charging and discharging power of the shared storage power station, the user can also sell part of the power to the external grid to ensure the maximum benefit for itself. In addition, since the period 18:00–22:00 belongs to the peak hours of the grid tariff, to minimize the operating cost, user 1 uses the shared energy storage plant to discharge a larger amount of electricity, so as to minimize the purchase of electricity from the grid and uses the shared energy storage plant to discharge a maximum power of 56.1882 kW during the period 18:00–19:00.

From Figure (b) and Figure 6, it can be seen that during the time period 10:00–17:00, the PV output is greater than the customer's electricity load, and the remaining PV output is stored inside the power plant through the shared energy storage plant. At other times, customers meet their electricity demand by purchasing power from the external grid and discharging it using shared storage plants. Especially in the period 07:00–09:00, its electricity demand is much larger than the PV output, and this period is not the valley time of power price, so it chooses to discharge from the shared storage power station, and the interactive power in the period 08:00-09:00 is the maximum of the whole day, reaching 108.5106 kW.

From Figure (c) and Figure 7 and combined with the results of power trading of other users, it can be concluded that the power consumption behavior of each user is generally consistent, purchasing large amounts of power during the grid electricity price valley hours and storing the surplus power in the shared energy storage plant, which will be prioritized to meet the power demand by discharging through the shared energy storage plant during the peak hours, thus reducing the operation cost. At the same time, for the external power grid, the operation mode and power purchase plan of users and shared energy storage plants can relieve the pressure of power supply during peak periods, with obvious peak-shaving and valley-filling effects. It can also be seen that in order to balance individual and overall benefits, the interaction of power is maintained between the user, the shared storage plant and the external grid for almost every period.

From Figure, it can be seen that the shared energy storage plant is in the discharging state during the hours 22:00–07:00 and 09:00–17:00, and in the charging state during the rest of the time. In the time period 16:00-18:00, the shared energy storage plant power reaches a maximum value of 0.9 Emax (Emax is the maximum capacity of the energy storage unit), and in the time periods 08:00– 09:00 and 21:00–22:00, the shared energy storage plant power reaches a minimum value of 0.1 Emax. The maximum discharge power of 74.2208 kW was reached at the shared energy storage plant during the period 11:00–15:00, and the maximum charging power of 114.9166 kW was reached at the shared energy storage plant during the period 18:00–19:00. After one cycle of operation, the shared energy storage plant finally returns to the initial state of 0.2 Emax, thus ensuring the normal operation of the next cycle. In addition, it can be seen from Figure 3–7 that the customer’s electric load is in balance and there is no abandonment of light, which is conducive to the accommodation of new energy.

Figure shows the transaction tariff between the shared energy storage plant and each industrial user entity. In order to reflect the price advantage of the trading model in this paper, it is assumed that the trading tariff among subjects is greater than the feed-in tariff.

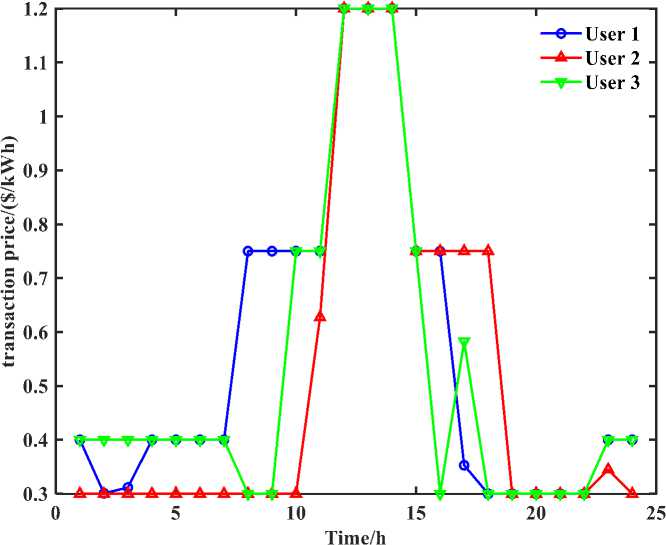
Figure 9. Electricity transaction price

Table 2 gives the comparison of operating benefits and operating costs before and after the cooperation of each subject, respectively. It can be seen that the total revenue of the main body of shared energy storage power plant in one cycle after Nash bargaining and cooperation increased by 233.7$, and the operating costs of the three user bodies decreased by 261.2$, 251.6$, and 151$, respectively, with a decrease of 73.1%, 45.3%, and 49.3%. This illustrates that both the shared energy storage plant and each user entity have significantly improved their own benefits through Nash bargaining cooperation, which shows that the method has achieved the expected goal by taking into account the overall and individual interests.

COMPARISON OF OPERATION INCOME BEFORE AND AFTER COOPERATION OF SHARED ENERGY-STORAGE POWER STATION

COMPARISON OF OPERATION COST BEFORE AND AFTER USER 1 COOPERATION

Table 2

Costs or benefits	Before cooperation	After cooperation	Revenue enhancement amount
Charging and discharging costs	0	-10.3	10.3
Trading with external grids	0	0.2	0.2
Transactions with users	0	243.8	243.8
Total revenue	0	233.7	233.7

Table 3

Cost	Before cooperation	After cooperation	Cost reduction
Demand-side response costs	13.5	13.5	0
Trading with external grids	343.8	238.4	105.4
Trading with energy storage plants	0	-155.8	155.8
Total Cost	357.3	96.1	261.2

Table 4

COMPARISON OF OPERATION COST BEFORE AND AFTER USER 2 COOPERATION

Cost	Before cooperation	After cooperation	Reduction
Demand-side response costs	14.6	13.5	1.1
Trading with external grids	540.8	251.1	289.7
Trading with energy storage plants	0	39.3	-39.3
Total Cost	555.4	303.8	251.6
Table 5 COMPARISON OF OPERATION COST BEFORE AND AFTER USER 3 COOPERATION
Cost	Before cooperation	After cooperation	Reduction
Demand-side response costs	14.6	13.5	1.1
Trading with external grids	291.9	269.8	22.1
Trading with energy storage plants	0	-127.8	127.8
Total Cost	306.5	155.5	151

This paper establishes the cooperative operation mode of shared energy storage power plant and industrial users based on Nash bargaining and transforms this problem into two sub-problems of system revenue maximization and power transaction payment bargaining for distributed solution. The analysis of the arithmetic examples leads to the following conclusions:

• 1.    The alternating direction multiplier method is used to solve the two subproblems of system revenue maximization and power transaction payment bargaining with good convergence, and this algorithm protects the privacy information of each participating subject, and also has the advantages of fast convergence and high accuracy, which completes the efficient solution of the cooperative operation problem in this paper.

• 2.    Through the analysis of the trading results of each body, the electric load of users reaches a balanced state, reducing the phenomenon of abandonment, which is conducive to the accommodation of new energy. For the power grid, the power consumption behavior of each body is conducive to relieving the pressure on the power grid and has an obvious effect of peak shaving and valley filling.

• 3.    In comparison with the pre-collaboration period, the overall revenue of shared energy storage plants and industrial users has increased, and the benefits of each subject have also been significantly improved, taking into account both the overall and individual interests.