Научные статьи \ Прикладные науки. Медицина. Технология \ Инженерное дело. Техника в целом \ Испытания материалов. Товароведение. Силовые станции. Общая энергетика

Оперативная оценка трещиностойкости сталей

Автор: Бахрачева Юлия Сагидулловна

Журнал: НБИ технологии @nbi-technologies

Рубрика: Технико-технологические инновации

Статья в выпуске: 4 (19), 2015 года.

Бесплатный доступ

Предложен метод прогнозирования трещиностойкости по результатам испытаний на растяжение. Предложенная модель показывает правомерность использования методов механики сплошных сред при анализе процессов, происходящих в зоне ограниченной пластичности перед фронтом трещины.

Трещиностойкость, фронт трещины, кривая течения, энергия пластической деформации, испытание на растяжение

Короткий адрес: https://sciup.org/14968412

IDR: 14968412 | УДК: 620.178:669.14 | DOI: 10.15688/jvolsu10.2015.4.7

Текст научной статьи Оперативная оценка трещиностойкости сталей

DOI:

Наличие в промышленности огромного парка оборудования с истекшим паспортным сроком службы постоянно ставит вопрос о правомерности продления срока эксплуатации. Это сложная задача, требующая наличия надежных методов оценки состояния металла в изделии. Крупногабаритные объекты, находящиеся в эксплуатации, не могут быть доставлены в лабораторию для проведения испытаний. Многие объекты работают столь долгое время, что методы расчета изделий подобного типа, а также критерии оценки пригодности к дальнейшей работе давно изменились. Это, в частности, относится к объектам, испытывающим воздействие переменных нагрузок. Последние приводят к росту трещин и вызывают опасность хрупкого или псевдохруп-кого разрушения.

Наиболее современным методом оценки склонности материалов к хрупкому разрушению является определение трещиностойкости K_Ic . При исследовании усталостных разрушений и остаточного ресурса все чаще применяются методы механики разрушения [3; 4; 6].

В данной статье рассмотрена возможность упрощения предложенной в работах [1; 2; 5] методики. С этой целью предложено в

вычислениях использовать среднее значение величины энергии пластической деформации в расчете на единицу поверхности в малой пластической зоне протяженностью r перед фронтом трещины. Для этого сначала была вычислена средняя величина интенсивности упруго-пластической деформации е i _ср в малой пластической зоне перед фронтом трещины:

1r е =- jefexp [-е fx / (1,155 • W )] dx = r0

= 1,1551 W !• 1 - exp

V r / I

( P • r

I ^е f ^r I

V 1,155 • W ))

После этого по обобщенной кривой течения определяли величину интенсивности напряжений о i _ср , соответствующую значению е i ср - Результаты расчетов для низкопрочных и высокопрочных сталей приведены в таблицах 1, 2.

После этого рассчитывали среднюю энергию пластической деформации на единицу поверхности в зоне ограниченной пластичности перед фронтом трещины:

γ cp

2 0,21 2 1 ^ • _е • r

2 i cp .

Таблица 1

Значения величин σ _в, ε _р и σ _ср, ε _ср для низкопрочных сталей

Сталь	Т , К	σ в , МПа	σ ср , МПа	ε р	ε ср
10Г2ФБ	293	630	573	0,118	0,148
	243	665	417	0,104	0,148
	213	690	710	0,101	0,148
	77	1020	1068	0,065	0,096
ВСт. 3кп	293	420	549	0,137	0,136
	243	510	306	0,135	0,130
	213	540	639	0,134	0,124
	77	910	1007	0,068	0,060
17ГС	293	555	482	0,119	0,127
	243	626	372	0,114	0,129
	213	630	545	0,109	0,121
	77	898	915	0,067	0,077
17Г1С-У	293	470	647	0,121	0,145
	243	590	361	0,115	0,138
	213	630	837	0,110	0,132
	77	915	1053	0,067	0,096
06Г2НАБ	293	562	483	0,114	0,174
	213	665	516	0,103	0,155
	77	948	908	0,063	0,124

Примечание. Здесь и в следующей таблице: σ _в – предел прочности; σ _ср– средняя величина интенсивности напряжений; ε _р – величина интенсивности упруго-пластической деформации; ε _ср – средняя величина интенсивности упруго-пластической деформации.

Таблица 2

Значения величин σ _в, ε _р и σ _ср, ε _ср для высокопрочных сталей

Материал	t зак , о С	t отп , о С	σ в , МПа	σ ср , МПа	ε р	ε ср
20CrMnMoVA	900	250	1481	1396	0,217	0,148
20CrMnMoVA	900	300	1457	1439	0,162	0,146
22CrMnSiMoVA	900	200	1543	1429	0,207	0,131
25SiMn2MoVA	900	200	1686	1547	0,199	0,119
		300	1624	1535	0,178	0,121
		200	1821	1608	0,233	0,124
		250	1784	1636	0,214	0,129
		300	1765	1653	0,221	0,149
		350	1770	1659	0,196	0,129
		400	1717	1633	0,182	0,129
42CrMoA	1170	200	2019	1746	0,155	0,068
30CrMnSiNi2A	900	200	1703	1521	0,233	0,110
		230	1676	1540	0,204	0,108
		250	1786	1555	0,304	0,121
		280	1655	1531	0,209	0,114
		300	1601	1514	0,198	0,121
CrNiMo	860	240	1754	1694	0,198	0,141
		290	1646	1547	0,245	0,146
		340	1675	1595	0,219	0,141
		400	1578	1529	0,199	0,144

Примечание. t _зак– температура закалки; t _отп – температура отпуска.

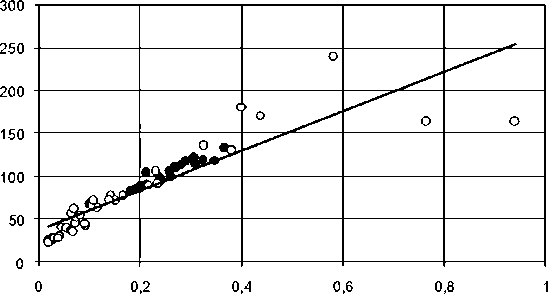
Результаты расчетов по формуле (2) для двух групп рассмотренных выше сталей показаны на рисунке 1.

Как видно на рисунке 1, зависимость К_Ic ( √γ _ср ) также описывается для высокопрочных и низкопрочных сталей одной прямой линией:

K Ic = 232 γ cp + 37. (3)

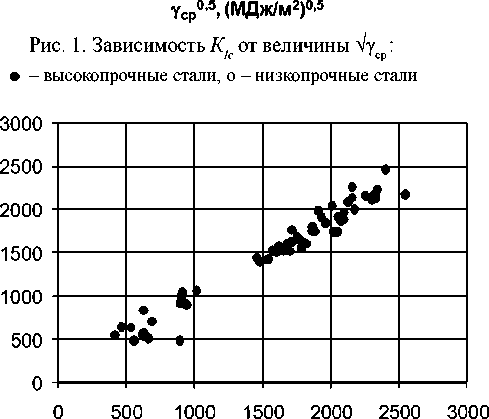
Результаты сравнения средних значений интенсивностей деформаций и напряжений с величинами равномерных деформаций и пределов прочности для исследуемых сталей приведены на рисунках 2 и 3.

i£

5 го

^ср’

МПа

Ов,МПа

Рис. 2. Зависимость σ от величины σ

^ср

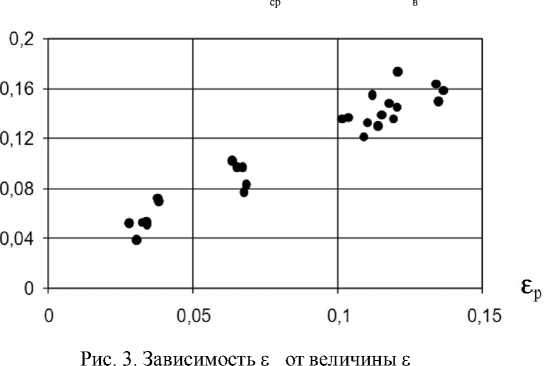
ср

Видно, что для всех рассмотренных сталей наблюдается линейная зависимость между ε _i _ср и ε _р , а также σ _i _cр и σ _в . Это дает возможность привести формулу (2) к следующему виду:

γ рав

σ₀ _, ₂ + σ_В

⋅ ε_р ⋅ r .

Расчеты по формуле (4) дают результат, аналогичный расчетам по формуле (2) (см. рис. 4).

Как видно из рисунка 4, зависимость К Ic ( √γ рав ) также линейна:

KIc =330 γ +36. (5)

Можно сделать следующие выводы:

1. Установлены закономерности соотношений трещиностойкости и удельной энергии пластической деформации слоев металла, прилегающих к поверхности разрушения, для сталей различных уровней прочности.
2. Предложен метод расчета среднего значения величины энергии пластической деформации в малой пластической зоне протяженностью r перед фронтом трещины.
3. Показана линейная зависимость между ε _i _ср и ε _р , а также σ _i _cр и σ _в , что позволило предложить упрощенный метод расчета энергии пластической деформации в упрочненном слое под поверхностью разрушения по стандартным механическим свойствам.

Список литературы Оперативная оценка трещиностойкости сталей

Бахрачева, Ю. С. Оперативная оценка склонности материалов к хрупкому разрушению при статическом и циклическом нагружении: дис.... канд. техн. наук/Бахрачева Юлия Сагидулловна. -Великий Новгород, 2004. -126 с.
Бахрачева, Ю. С. Оценка вязкости разрушения сталей по результатам контактного деформирования/Ю. С. Бахрачева//Вестник Волгоградского государственного университета. Серия 10, Инновационная деятельность. -2012. -№ 2. -С. 53-56. -DOI: DOI: 10.15688/jvolsu10.2012.2.9
Влияние содержания азота на структуру и свойства нитроцементованной стали/В. И. Шапочкин //Металловедение и термическая обработка металлов. -2010. -№ 9. -С. 12-18.
Дрозд, М. С. Аналитическое исследование напряженного состояния при внедрении упругой сферы в упругопластическое полупространство/М. С. Дрозд, А. П Осипенко//Металловедение и прочность материалов: межвуз. сб. науч. тр. ВолгГТУ. -Волгоград: Изд-во ВПИ, 1975. -С. 12-19.
Красовский, А. Я. Трещиностойкость сталей магистральных трубопроводов/А. Я. Красовский, В. Н. Красико. -Киев: Наукова думка, 1990. -176 с.
Медведев, Р. С. Применение статистических методов управления качеством для оптимизации производства по ремонту пути/Р. С. Медведев, Ю. С. Бахрачева//Вестник Волгоградского государственного университета. Серия 10, Инновационная деятельность. -2014. -№ 3 (12). -С. 93-97. -DOI: DOI: 10.15688/jvolsu10.2014.3.11
Шапочкин, В. И. Нитроцементация в условиях периодического изменения состава ат-Ю. С. Бахрачева//Материаловедение. -2010. -№ 8. -С. 52-58.
Bakhracheva, Yu. S. The Method for Lifetime Estimation Through the Mechanical Properties in Tension/Yu. S. Bakhracheva//Вестник Волгоградского государственного университета. Серия 10, Инновационная деятельность. -2014. -№ 2. -С. 27-32. -DOI: DOI: 10.15688/jvolsu10.2014.2.4
Valve Cam Design Using Numerical Step-By-Step Method/A.V. Vasilyev, Yu. S. Bakhracheva, O. Kabore, Yu.O. Zelenskiy//Вестник Волгоградского государственного университета. Серия 10, Инновационная деятельность. -2014. -№ 1. -С. 26-32. -DOI: DOI: 10.15688/jvolsu10.2014.1.4

Еще