Оперативно-календарное планирование сборочных технологических процессов радиоэлектронных изделий

Современное радиоэлектронное изделие состоит из большого числа деталей и сборочных единиц (ДСЕ), в его производстве используется широкая номенклатура материалов и покупных комплектующих изделий (ПКИ). Число наименований деталей в изделии может достигать нескольких десятков тысяч, что значительно усложняет радиоэлектронное производство и требует особого подхода к его организации. Задачи оперативно-календарного планирования на таких производственных предприятиях ставятся как задачи обеспечения выпуска продукции в заданных объемах, в нужном ритме и высокого качества.

К предприятиям, выпускающим сложные радиоэлектронные изделия, относится открытое акционерное общество «Научно-производственное предприятие «Радиосвязь» – ведущее российское предприятие по разработке и серийному изготовлению наземных станций спутниковой и тропосферной связи, а также навигационных систем и комплексов. При этом среди всех производственных процессов радиоэлектронного производства особое место занимают технологические процессы сборки радиоэлектронных изделий.

Технологический процесс сборки изделий на предприятии является составной частью производственного процесса, который последовательно соединяет детали в сборки, узлы, комплексы, из них получается готовое изделие, отвечающее техническим требованиям.

Ведущими элементами производственной структуры при выполнении технологических процессов сборки изделий выступают сборочные цеха, в которых завершается цикл изготовления изделий. Важной особенностью сборочных цехов служит то, что на этапе сборки стоимость незавершенного производства приближается к предельной величине – себестоимости готовой продукции. Поэтому сокращение длительности цикла сборки обеспечивает не только ускорение оборачиваемости оборотных средств, но и наиболее эффективное использование производственных площадей. При этом уровень автоматизации сборочных производств в России крайне низок, а трудоёмкость данного вида работ в единичном и мелкосерийном производстве составляет 20–60 % от общей трудоёмкости производства в приборостроении.

Сборочный процесс может осуществляться в следующих вариантах:

• •    сборка под механическую обработку (сборочные единицы проходят операции расточки, фрезерования);

• •    сборка под сварку; общая сборка (окончательная);

• •    узловая сборка (сборочные единицы входят в изделие);

• •    сборка под испытания (тестирование изделия при различных режимах его работы).

Методы исследования

Организация производственного процесса сборки в ОАО «НПП «Радиосвязь» определяется характером выпускаемой продукции, типом производства и может быть представлена как поточная форма организации, которая характеризуется глубоким расчленением процесса сборки на операции, их последовательным выполнением на специализированных рабочих местах. При этом оперативное управление сборочным производством заключается в распределении – 780 –

полученного плана работ или части плана среди рабочего персонала во временном периоде и по очередности выпуска комплектов заказов.

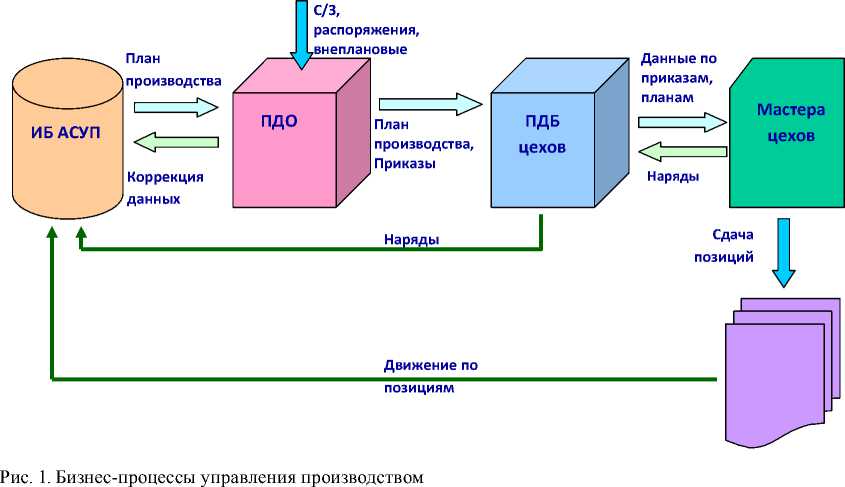
Схема существующих бизнес-процессов управления производством ОАО «НПП «Радиосвязь» представлена на рис. 1.

Формирование плана работ осуществляется иерархической системой планирования различных уровней. С верхнего уровня планирования в планово-диспетчерский отдел (ПДО) поступают служебные записки, распоряжения и внеплановые задания, которые являются основанием для запуска формирования плана производства. Далее план постепенно спускается вниз до производственного уровня, где непосредственно проходят фактические работы по данному плану.

Полученный номенклатурный план не может быть сразу принят к исполнению. На каждом этапе он подвергается коррекции. После формирования плана ПДО создает приказы на позиции с отсутствующим технологическим маршрутом и корректирует план. На следующем этапе планово-диспетчерские бюро (ПДБ) цехов проверяют правильность оперативного планирования и вносят информацию о произведенных позициях, данные о которых не были учтены при планировании. Мастера цехов корректируют очередность запуска деталей, поскольку плановые органы рассчитывают план, опираясь на показатели, заложенные только в технологии изготовления каждого изделия, и не учитывают загрузку производства, наличие свободного рабочего персонала, оборудования и других факторов.

Однако процесс формирования плана в сборочном производстве отличается от плана заготовительного и механосборочного производства. Для сборочного производства важно иметь информацию о состоянии сборки по каждому комплекту заказа, в то время как для заготовительного и механосборочного производства это второстепенная информация.

На рис. 2 представлена укрупненная схема информационных потоков при планировании. Для получения номенклатурного плана производства необходимо наличие данных о составе – 781 – изделия (конструкторская документация и ведомость применяемости), технологических процессах изготовления (технологическая документация) и график товарного выпуска. Конструкторская документация определяет состав изделия. Информация о технологических процессах используется для установления очередности операций и цехов по изготовлению позиций. График товарного выпуска определяет номенклатуру заказов, очередность выпуска и количество комплектов. Вся информация передается в информационную базу АСУП для формирования номенклатурного плана для цехов предприятия.

В соответствии с планом сборочные цеха формируют заявки в центральный комплектовочный цех (ЦКЦ) и после комплектования запускают ДСЕ в производство. По результатам выполненных работ формируется отчетность (наряды) для начисления заработной платы и коррекции оперативной картотеки.

На предприятии ранее были разработаны и успешно применяются информационные системы:

• –    учета движения товароматериальных ценностей;

• –    управления закупками;

• –    учета деталей и сборочных единиц;

• –    планирования производства [1].

Интеграция данных модулей со сторонними информационными системами управления производством вызывала дополнительные трудности, поэтому было принято решение разработать собственную систему диспетчеризации производства, обеспечивающую выполнение следующих функций:

Бухгалтерия

Конструкторское бюро

Технологический отдел

Производственный отдел

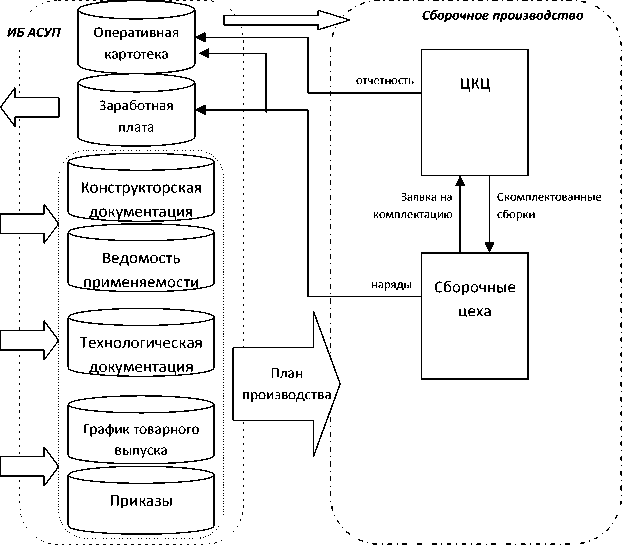
Рис. 2. Схема информационных потоков при планировании

• –    диспетчеризация производства – управление потоком изготавливаемых деталей по операциям, заказам, партиям, сериям посредством рабочих нарядов;

• –    управление документами – контроль содержания и прохождения документов, сопровождающих изготовление продукции, ведение плановой и отчетной цеховой документации;

• –    отслеживание истории продукции – визуализация информации о месте и времени выполнения работ по каждому изделию.

Для разработки системы диспетчеризации производства была выбрана трехуровневая архитектура на базе веб-технологий, что обеспечило кроссплатформенность и низкие требования к производительности оборудования на уровне клиентских устройств, относительную легкость обновления и сопровождения программного обеспечения.

Для обеспечения функций оперативно-календарного планирования на цеховом уровне состав системы диспетчеризации производства дополнен модулем оптимизации на базе методов оперативного управления, обеспечивающих сокращение производственного цикла при выполнении технологических операций на производствах единичного и мелкосерийного типа через построение оптимальных календарных планов-графиков производственных процессов.

В задаче планирования работы сборочного цеха на известном составе оборудования, объеме заказов учитываются занятость и календари работы оборудования, основных и вспомогательных рабочих, возможность использования групп взаимозаменяемого оборудования и другие факторы технологического и организационного плана. При этом используется ряд различных критериев планирования временного и стоимостного характер, и выбор конкретного критерия планирования зависит от текущей производственной ситуации в цехе.

С математической точки зрения задача оперативно-календарного планирования представляет собой сложную комбинаторную задачу, имеющую множество решений, среди которых необходимо найти оптимальное в смысле некоторого критерия. Эта задача может быть решена точно или приближенно. Основными критериями оптимальности являются: минимизация общей длительности производственного цикла, минимизация времени переналадок, критерий минимума стоимости выполненного расписания и т.д. Поиск оптимального или «близкого» к оптимальному оперативно-календарного плана может осуществляться с помощью методов линейного программирования, комбинаторных или эволюционных методов.

В результате анализа существующих систем и методов оперативно-календарного планирования было принято решение об использовании эволюционных методов как методов глобальной многокритериальной оптимизации, позволяющих получать оптимальные решения проблем реальных производственных ситуаций за малое время. Среди эволюционных методов перспективным решением сложных комбинаторных задач оптимизации является использование метода муравьиных колоний и его модификация с введением «элитных» муравьев, которые «усиливают» лучшие маршруты, найденные с начала работы алгоритма. Преимуществом данного алгоритма для поставленной задачи является то, что данный метод не требует построения структурной модели непосредственно самого производственного участка.

Согласно теории расписаний задача оперативно-календарного планирования запишется как задача обработки партии из n деталей на m станках: n/m/G/Cmax [2]. Применительно к процессам сборочного производства под деталями будем понимать технологические операции, – 783 – под станками – устройство/рабочий (слесарь-сборщик, токарь и т.д.). Далее будем использовать терминологический аппарат теории расписаний.

Пусть даны множества M = {M₁,…,M_m} – заданное количество станков; J = {J₁,…,J_n} – заданное количество деталей; O = {O 1 ,…,O n } – заданное количество операций. Для каждой операции u_ij ∈ O есть деталь J_i , которой она принадлежит, станок M_j , на котором она должна быть обработана, и продолжительность обработки p ij операции u ij , где p ij – неотрицательное целое число. Требуется найти стартовые времена всех операций таким образом, чтобы время завершения самой последней операции было минимально. Для каждой детали должна быть соблюдена последовательность операций, каждый станок может обработать только одну деталь за заданное время . Требуется выбрать такую последовательность обработки деталей на станках, т.е. составить расписание, для которой период обработки C_max будет минимальным при удовлетворении всех ограничений .

minC max = min { max ( S jj + p ij ) : V J i e J, V M j e m } .

Обобщенная схема работы алгоритма составления оперативного плана с применением метода муравьиных колоний сводится к построению модели сборочного процесса в виде направленного графа; формированию муравьиной колонии, поиску решения с учетом установленных ограничений.

Сборочный процесс представлен дизъюнктивным графом G = (V, A, E) , где V – набор узлов, A – соединительный набор дуг, E – дизъюнктивный набор дуг [3]. Узлы V соответствуют всем операциям и двум фиктивным узлам, источнику и выходу. Соединительные дуги A представляют отношения предшествования между операциями для каждой детали, а дизъюнктивные дуги E – все пары операций, которые будут выполнены на том же самом станке. Всем дугам, исходящим от узла, присваивается продолжительность обработки операции. У источника фиктивной операции Ос , есть соединительные дуги нулевой длины для всех операций каждой детали, обрабатываемых на первом станке, а у выхода – фиктивной операции Оф – есть соединительные дуги, исходящие из всех операций, выполняемых на последнем станке. Выполняемое планирование соответствует выбору одной дуги от каждой дизъюнктивной дуги и соединения таким образом, чтобы получающийся направленный граф был нециклическим.

На рис. 3 представлен дизьюнктивный граф для решения задачи составления расписаний 3/3/G/Cmax , где Оij – операции обработки i -й детали на j -м станке.

Дуги, соединяющие операцию О ij с операцией О iu , являются соединительными дугами. Дуги, соединяющие операцию О_ij с операцией О_bu, – дизъюнктивные дуги.

Формирование муравьиной колонии включает определение количества муравьев в соответствии с заданным технологическим процессом сборки (для модифицированного муравьиного алгоритма (ММА) определяется количество «элитных» муравьев как 1 % от общего количества муравьев), правила коррекции концентрации феромона, правила поведения муравьев при построении решения в виде вероятностей перехода.

Результаты исследований

Общая схема реализованного алгоритма муравьиной колонии:

• 1.    Формирование графа технологического процесса сборки.

• 2.    Инициализация параметров алгоритма.

• 3.    Создание муравьиной колонии и размещение ее в начальном пункте.

• 4.    Построение схемы переходов между вершинами графа.

• 5.    Выбор наиболее оптимального расписания.

• 6.    Обновление феромона.

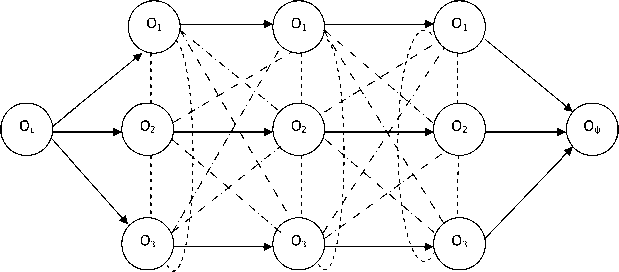
Рис. 3. Дизъюнктивный граф 3/3/G/Cmax

Шаги 3–6 повторяются, пока не будет достигнуто условие останова алгоритма, которым является заданное число итераций.

Инициализируемые параметры алгоритма:

• α – вес следа феромона. При α = 0 выбор короткой операции наиболее вероятен, алгоритм становится жадным;

• β – видимость при выборе маршрута. При β = 0 выбор происходит только на основании феромона, что приводит к субоптимальным решениям;

• q₀ – параметр, принимающий значение из интервала [0,1];

• p – коэффициент испарения феромона, p ∈ [0,1] ;

• Q – значение порядка длины оптимального пути.

Матрица видимости D формируется в виде

D=

	1	2		n
1	1 p 11	1 p 21		1 p n 1
2	1 p 12	1 p 22		1 p n 2
m	1 p 1 m	1 p 2 m		1 p p nm

Между регулируемыми параметрами α и β необходим компромисс, который находится экспериментально.

Количество муравьев (ant_count) в партии определяется числом вершин в дизъюнктивном графе. Количество партий муравьев (group_count) задается произвольно. Все муравьи помещаются в одну стартовую точку – Oс на дизъюнктивном графе. В алгоритме процедура поиска оптимального расписания проходит по каждому k-му муравью, пока k не достигнет значения – 785 – ant_count в l-й партии, т.е. осуществляется ant_count×group_count последовательных циклов. На каждом шаге цикла k-го муравья определяется место в расписании для одной из работ l-й партии.

На этом же этапе задаётся начальный уровень феромона, который инициализируется небольшим положительным числом для того, чтобы на начальном шаге вероятности перехода в следующую вершину графа не были нулевыми.

Матрица феромонаформируется в виде

	O 11	O 12	—112—	O nm
O 11	0	T 11,12		T 11, nm
O 12	7 12,11	0		T 12,nm
O nm	T nm,11	T nm, 12	…	0

В каждой итерации алгоритма каждый муравей пошагово строит путь до конечной вершины. При этом в каждой вершине каждый муравей должен выбрать следующую дугу пути из списка кандидатов, являющегося подмножеством списка непосещенных вершин. Выбранные вершины последовательно добавляются в список посещений. Если муравей k находится в вер-k шине ij, он выбирает следующую вершину bu е Nij на основе вероятностей перехода.

При пустом списке посещений муравей k выбирает операцию из списка кандидатов согласно двум правилам перехода, комбинирующим информацию о феромоне и эвристическую информацию [4].

bu^k ( t ) =

t ag max j^{T k}hg ^{( t} ^Ь j^hg ⁽ t^

L hg e Ck ( t )

bu

iq ^ q о oterwise

где τ _ij,_hg – уровень феромона между операциями ij и hg ; η _ij,_hg – эвристическое расстояние между операциями ij и hg ; C^k – список возможных кандидатов-операций, которые муравей может посетить, после выполнения предыдущей операции; q – случайное число, однородно распределенное в [0,1]; q 0 – параметр, определяющий, будет ли следующая операция выбрана в соответствии с точным правилом (1).

Вероятность случайного выбора следующей операции из списка кандидатов [4] определяется по выражению pk (t ) = ij,buv'

[ ^T k , bu ^{( t )l}' ⁿ jbu ^{( t )в}

_T k    ₍

Z , J ij, bu hg G C^k ( t )^[

> k , bu ( - f

if bu G C^k ( t )

oterwise

Когда муравей выполнил операцию, он перемещается из списка непосещенных операций в список посещенных и, соответственно, удаляется из списка операций-кандидатов. Процедура повторяется, пока муравей не посетит все вершины в графе. Последовательность всех операций в посещаемом списке представляет собой полный порядок обработки партии из n деталей на m станках, что однозначно определяет решение задачи.

Выбор наиболее оптимального расписания определяется параметром L^k . L^k – время обработки партии деталей на всех станках, т.е. время обработки всех операций в графе, пройденных k -м муравьем, от первой до последней вершины пути, рассчитанного по формуле (1). Если найденное значение L^k для k -го муравья меньше, чем хранимое значение C max , то C max принимает значение L^k , список посещений k -го муравья принимается лучшим на данный момент выбранным маршрутом и сохраняется как оптимальный.

Когда все муравьи в рамках технологического процесса сборки построили полный путь от начальной до конечной вершины, каждый муравей помечает свой путь, откладывая для каждой дуги феромон в соответствии со следующим выражением [4]:

Ат kj , bu ( t ) =

I -Q-L^ ( t ) ’ 0

j, , bu ) e V^k ( t ) ( ij , bu ) ^ V ^k ( t )

Здесь V^k(t) – маршрут, пройденный муравьём k к моменту времени t .

Правила внешней среды определяют правило испарения феромона с коэффициентом испарения p ∈ [0,1], которое имеет вид [4]

^T ij , bu tt + 1 ) = ( 1 - P У ^T jbu ⁽ t ) + ^Ат ij , bu ^{( t} )

m

ATij,bu (t) = Ё ATj,bu (t)> k-1

где m – количество муравьёв в колонии. Из (4) следует, что общая концентрация феромона для данной дуги пропорциальна «качеству» путей, в которые входит эта дуга.

Для улучшения временных характеристик муравьиного алгоритма вводятся «элитные» муравьи, которые усиливают ребра наилучшего маршрута, найденного с начала работы алгоритма. Количество феромона, откладываемого на ребрах наилучшего текущего маршрута C_max , принимается равным, ^Q _L + где L⁺ – длина маршрута C max .

Этот феромон побуждает муравьев к исследованию решений, содержащих несколько ребер наилучшего на данный момент маршрута C max . Если в муравейнике есть e элитных муравьев, то ребра маршрута C_max получат общее усиление [4]

At e = e • Q- . (5)

В модифицированном алгоритме муравьиной колонии (ММА) к инициализируемым параметрам алгоритма добавляют определение числа элитных муравьев e . Если на шаге 5 значение C max было обновлено, то на шаге 6 добавляется обновление феромона в соответствие с (5).

На рис. 4 представлен результат апробации алгоритма составления оперативного плана цехового уровня для задачи 9/5/G/C max на основе модифицированного муравьиного алгоритма в виде диаграммы Ганта после оптимизации [5].

Пробная версия модуля оптимизации, который в дальнейшем войдет в состав системы диспетчеризации производства, разработана в виде расширяемого приложения и содержит библиотеку методов оперативного управления (ОУ), реализованную через DLL-файлы.

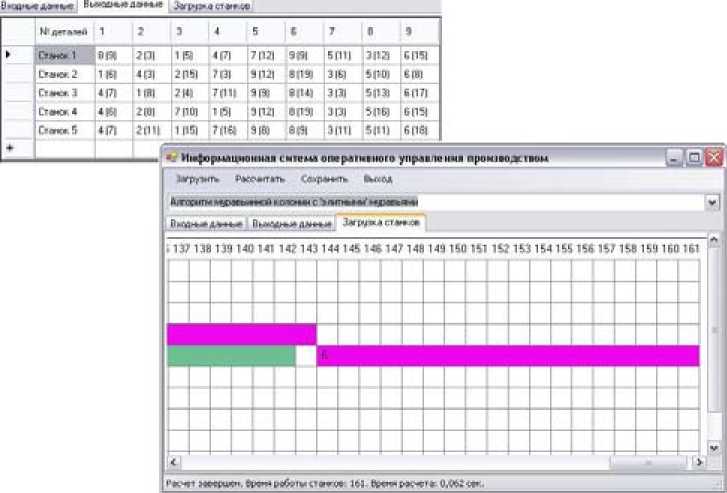
Рис. 4. Результат работы модуля оптимизации

Сборки NET в составе расширяемого приложения:

• •    CommonSnappableTypes.dll – сборка с определениями типов, используемых каждой интегрируемой оснасткой, на которую напрямую ссылается приложение WindowsForms;

• •    AntColony.dll, AntColonyElite.dll и др. – интегрируемые оснастки на С#, которые используют типы из сборки CommonSnappableTypes.dll;

• •    Production.ехе – приложение WindowsForms, функциональные возможности которого расширяются каждой интегрируемой оснасткой.

При разработке были комплексно использованы динамическая загрузка, рефлексия для проверки отдельных двоичных файлов, создаваемых другими производителями, на предмет их способности выступать в роли подключаемых оснасток и позднее связывание для обеспечения динамического получения ссылки на требуемую инфраструктуру и приведения в действие лежащих в ее основе функций.

Библиотека методов ОУ разработанного модуля оптимизации для составления расписания цехового уровня включает метод Джонсона, метод Петрова-Соколицина, метод ветвей и границ (МВГ), модифицированный метод ветвей и границ (ММВГ), метод муравьиной колонии (МА), модифицированный метод муравьиной колонии с введением «элитных» муравьев (ММА).

Среди всех реализованных методов наиболее эффективно решают задачу оперативнокалендарного планирования методы ветвей и границ, муравьиной колонии и их модифика- – 788 –

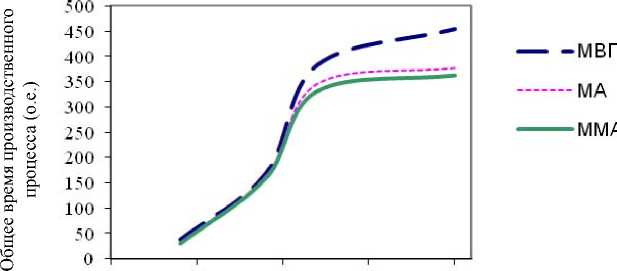
О 5        10       15       20

Количество технологических операций (шт.)

Рис. 5. Зависимость длительности производственного цикла от количества технологических операций

Таблица 1

Количество технологических операций (детали) Количество технологических устройств (станки) Общее время производственного цикла (относительные единицы) МВГ МА ММА 4 3 37 32 30 9 5 168 164 161 16 16 383 346 332 20 16 454 377 363 ции. Для оценки эффективности методов был проведен вычислительный эксперимент выполнения задачи оперативно-календарного планирования вышеуказанными методами по критерию минимизации общего времени выполнения технологических операций с учетом времени работы алгоритмов. Результаты расчетов приведены на рис. 5, часть из которых сведена в табл. 1.

В результате моделирования производственного процесса при составлении расписания сборочного участка методом муравьиной колонии общее время выполнения 20 операций 16 ра-бочими/устройствами сократилось на 17 % по сравнению с расписанием, полученным методом ветвей и границ. Применение модифицированного метода муравьиной колонии с введением «элитных» муравьев улучшает общее время выполнения технологических процессов в среднем на 5 % с одновременным сокращением длительности расчетов в несколько раз.

Выводы

В данной статье предложен алгоритм оперативно-календарного планирования для сборочных процессов с применением инструментальных возможностей муравьиных алгоритмов, реализованный в составе библиотеки методов оперативного управления модуля оптимизации системы диспетчеризации производства.

Программная реализация алгоритма муравьиной колонии и модифицированного алгоритма муравьиной колонии с «элитными» муравьями в рамках библиотеки методов оперативного управления позволяет оптимизировать оперативно-календарные планы сборочных производств по выбранному критерию – минимизация суммарной длительности технологического процесса сборки. В зависимости от выбора метода расчета расписания при прочих равных условиях результаты оптимизации варьируются в пределах 1-25 % как сокращения времени выполнения всех технологических операций, так и сокращения времени расчета плана. Оптимизация оперативно-календарных планов, вызывающая сокращение длительности производственного цикла, приводит к повышению рентабельности капитала в целом, повышению фондоотдачи и увеличению объема производства.

Проведенные многочисленные вычислительные эксперименты на контрольных примерах показали, что эффективность муравьиного алгоритма и в особенности его модификации с введением «элитных» муравьев растет при увеличении размерности задачи.