Оперативный метод анализа переходных процессов в электрических цепях (концепция и реализация инженерного метода)

Переходные процессы (ПП) в электрических цепях (ЭЦ) – специфический режим работы ЭЦ, что отражают математические модели (ММ) процессов, отличающиеся от ММ стационарных (установившихся) процессов, а также их возможные последствия.

Внимание к переходным процессам также определяет то обстоятельство, что прогрессирующее применение цифровой электроники делает их элементом нормального функционирования устройств наравне со стационарными режимами, а не эпизодическими явлениями при включении или выключении (коммутациях), что характерно для аналоговых устройств.

Классический метод описания переходных процессов как сумма частного решения неоднородного дифференциального уравнения и общего решения однородного уравнения зачастую вызывает затруднения при физической интерпретации решения, так как понятия принужденного и свободного состояний ЭЦ - только удобная математическая модель, обеспечивающая расчет переходных процессов в линейных цепях [1].

Предложенный метод (инженерный) исходит только из физических процессов в ЭЦ.

Переходный процесс – изменение во времени параметров ЭЦ (токов, напряжений, зарядов), содержащей реактивные элементы (индуктивности, конденсаторы – РЭ, рис. 1), при переходе ЭЦ из одного стационарного

ИССЛЕДОВАНИЯ

Havko____________

Ж ГРАДА

(установившегося) состояния в другое. На схеме эти состояния определяют два положения ключа (Кл).

Анализ переходных процессов предполагает определенные начальные условия, то есть значения токов и напряжений в ЭЦ при t = 0. Если непосредственно перед коммутацией (замыкание или размыкание Кл) все токи в ветвях и напряжения на пассивных элементах ЭЦ равны нулю, то имеют место нулевые начальные условия. И токи в ветвях с индуктив- 40 ными элементами и напряжения на конденсаторах при переходных процессах начинают изменяться с нулевых уровней. При ненулевых условиях – с тех уровней, которые они имели непосредственно до коммутации [2].

После коммутации, используя правила Кирхгофа, состояние ЭЦ (зависимости между токами и напряжениями) описывают дифференциальными уравнениями первого порядка [1]:

dLt) = -Rdt и duCCt) =-Xdt. iL(t)      L        uC (t)

Результат интегрирования уравнений –

Е     - -- iL (t) = —(1 - e T) и uc (t) = E (1 - e T) при подклю-

R        E -*-- чении и iL (t) =—e т и uC (t) = Ee т при отключении РЭ от источника E (τ – постоянные времени RL и RC ветвей, характеризующие динамику переходного процесса, равные соответственно L и RC).

Обобщая полученные результаты и предваряя дальнейшие построения, первый и второй результаты обозначены как

У(t) = АУ(1 - e") и У (t) = АУe"Т, где У и ДУ - соответственно уровень и приращение уровня параметра (тока, напряжения), отражающие возрастающую и убывающую d [ E - iL (t) R ]    R       d [ E - Uc (t)]     1

t иI                                         t

E - iL (t) R      L E - uC (t) R при подключении РЭ к источнику E (рис. 1, а, где в первом случае РЭ – L, во втором – C).

При отключении РЭ от источника Е экспоненциальные зависимости при нулевых начальных условиях (рис. 2, а, б).

Приведенные результаты позволяют перейти к рассмотрению переходных процессов при ненулевых начальных условиях.

В графическом представлении фрагменты состояний параметров при ненулевых на-

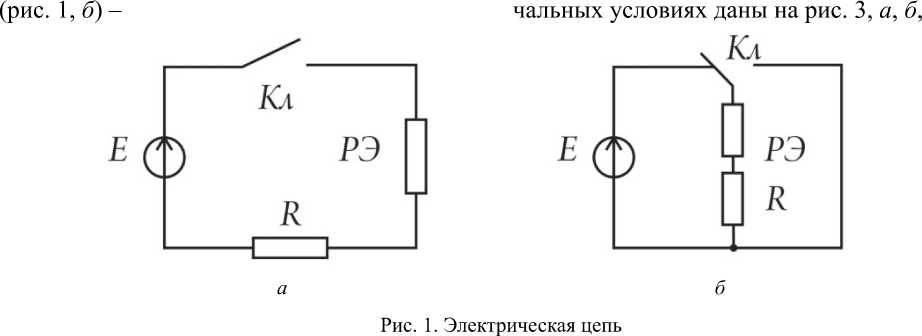
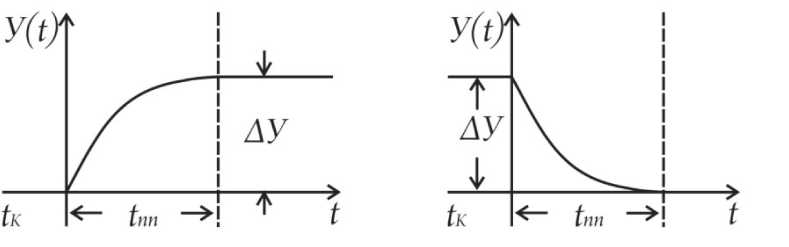
а

б

Рис. 2. Графики приращений параметров при переходных процессах: t_к = 0 – момент (начало) коммутации, t_пп – продолжительность переходного процесса

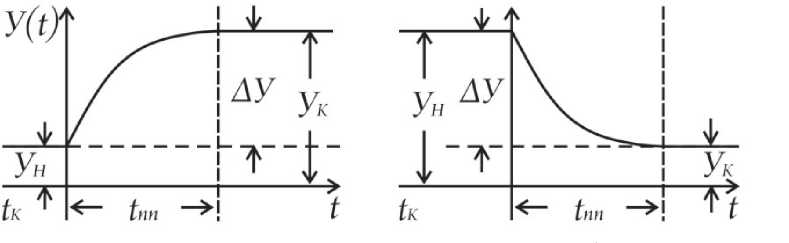
Рис. 3. Фрагменты состояния параметров переходных процессов: У_н и У _к – соответственно начальный и конечный уровни параметров, отражающие стационарные состояния в ЭЦ до и после переходных процессов.

Таким образом, если до коммутации ( t_к = 0) уровень параметра (начальный) был У н , а после t_K + t стал У _к (конечный), то переходный процесс определяет приращение уровня Δ У :

ау = |У н - У J в интервале tпп.

Это обусловлено тем, что процессы в ЭЦ, содержащих РЭ ( L, C ), обусловлены скоростями изменения токов или напряжений ( di/dt, du/dt ) и не зависят от стационарных начальных уровней. То есть только приращения уровней параметров на временном промежутке t_пп запускают соответствующие переходные процессы.

Это хорошо иллюстрирует операторное представление переходного процесса:

L {f'(t)} .=' PF(Р) — f (0), то есть при наличии исходного уровня [Ун = f(0)] он исключается из формирования переходного процесса, и в обоих случаях [f(0) = 0 – нулевые начальные условия и f(0) ≠ 0 – ненулевые начальные условия] его картину определяет только компонента pF(p) – производная от f(t).

Это позволяет сформулировать алгоритм получения математических моделей переходных процессов в ЭЦ при ненулевых начальных условиях, именуемый далее инженерным методом:

– применяя правила Кирхгофа (или другие методы расчета), определяют уровни параметров стационарных состояний ЭЦ до начала переходного процесса (У _н ) и после его окончания (У _к );

• -    сопоставляя полученные уровни, определяют приращения (ΔУ) соответствующих параметров (токов, напряжений, зарядов);

  – один из уровней (У _н или У _к ) принимают за уровень условного нуля - У ( У 0 ), относительно которого рассматривают развитие переходных процессов;

  – для отражения хода переходного процесса используют математические модели, полученные при описании переходных процессов для нулевых начальных условий:

У( t ) = ΔУ∙ЭМ1 и У( t ) = ΔУ∙ЭМ2, t                    _- 1

где ЭМ1 - (1 - e ^т ) , а ЭМ2 - e ^т (соответствующие экспоненциальные множители);

• -    к полученным результатам добавляют исключенные уровни условного нуля [У(У₀)] и получают окончательные математические модели соответствующих переходных процессов.

Для иллюстрации представлены примеры описания переходных процессов в простых ЭЦ, полученные операторным и инженерным методами.

На рис. 4 - традиционное и операторное представление электрической схемы, содержащей источник ЭДС ( E ), R и L элементы. В исходном состоянии (Кл разомкнут) ток, протекающий в ветви L , равен .

• 2    R

R R              R R

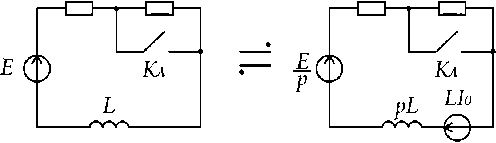
Рис. 4. Электрические схемы с элементами E, R и L

U ИССЛЕДОВАНИЯ

Havko-

ЖГРАДА

При коммутации (замыкание ключа)

E LE

+ ——

I _{( p} ) = E ⁽ P ) ^{+ LI} 0 = p ^{2 R} = ^{v p}    R + pL    R + pL

E 1    0,5 E L

=--I-- pR + pL R R + pL

E 1      0,5 E L

=--7------^ +----

Результат соответствует тому, который получен операторным методом, но более простыми средствами.

Второй пример (рис. 6).

R p

R

E L ₊ 0,5 E

R f R ) R

P I P ⁺ L I

RR

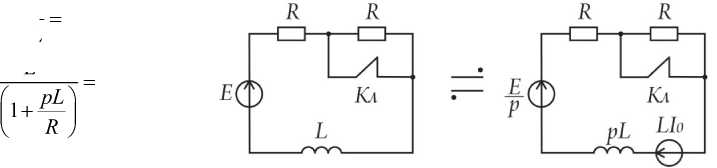
Рис. 6. Электрическая схема

R p ⁺ L

E a +

R p ( p + a )

0,5 E

R p + a

=•

•

Исходное состояние – Кл замкнут.

E LE

— + —

. E,,    —\  0,5 E —-

. = •    (1 — e ^T ) + -— e

• R          R

I _(px = ^E ( P ) + ^LI о = P R ^k p 2 R + pL 2 R + pL

—

E 0,5 E -

—

RR

e

Е         — t

= R (1 - 0,5 e ^т) = i ( t ).

Применение инженерного метода предпочтительно начать с графического представления переходного процесса (рис. 5).

ток после размыкания Кл.

После преобразований, аналогичных первому примеру, –

I ( p ) =

0,5 E   a „ 1

---+ E---

R P ( P + a )

=•

•

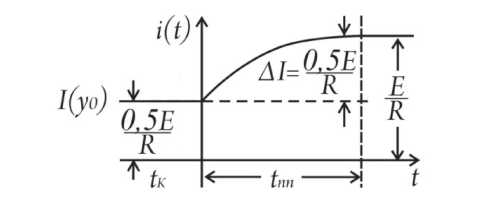
Рис. 5. Графическое представление переходного процесса

• = • °^ (1 - e" ) + Ee

p + a

0,5 E 0,5 E - t , + , e ^T

RR

0,5 E     - t_x   ,х

—— ⁽1 + e ^т ) = i ( t ) .

R

Графическое представление переходного процесса – рис. 7.

После коммутации ( t_к = 0) начинается переходный процесс с исходного стационар-

Г 0,5 E ного уровня I I =

за уровень условного нуля I ( у ₀) =

, который принимают

0,5 E

. Тогда R

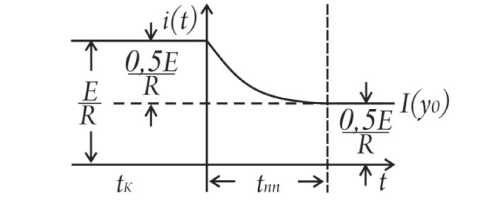
Рис. 7. Графическое представление переходного процесса

- ^t

i ( t ) = M • ЭМ1 = ⁰,⁵- (1 - e T ) -

R изменение тока относительно условного нуля (черта снизу). Окончательный результат:

i ( t ) = i ( t ) ⁺ I ⁽ У a ) =

0,5 E        - -_x 0,5 E

= —---(1 - 0,5e T) + —---=

RR

E 0,5 E - ^- E       -\

=--- e ^T = — (1 - 0,5 e ^T ).

RR R

На рис. 7: — - ток исходного (докомму-. R                        0,5 E тационного) стационарного уровня;

R

–

ток конечного (посткоммутационного) уровня, который является уровнем условного нуля; ^{0,5 E} = М - изменение тока между двумя стационарными уровнями за время t_пп . Тогда

- ^t

i ( t ) = А i ■ ЭМ 2 = -,-- e ^т -

R

ММ переходного процесса относительно ус-

ловного нуля и

0 SE - t

i ( t ) = i(t) + i ( y - ) = -,— e ^T +

R

, 1 (0 + ) = E — u c ⁽⁰ - ) = 150 - 50 = ₂₍ А ),

0,5 - +

R

0,5 -R

t — (1 + e ^T ).

(1 e )•

1 2⁽⁰ + ) пр

u_c (0 - ) R

= 1( А ).

Оба способа (операторный и инженерный) дают одинаковый результат.

Далее - сравнение классического и инженерного методов. Использован пример из [2] – рис. 8.

Тогда i3(0+) = ix(0+ ) - i2(0+) = 1( А).

Свободные составляющие токов и напряжений при t (0 ₊ ) - разности между полными и принужденными значениями:

R R h

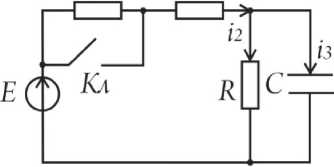
Рис. 8. Электрическая схема

По условиям – E = 150 В, R = 50 Ом, C = 100 мкФ.

Токи, протекающие в ветвях схемы ( i 1 , i i 3 ) после коммутации, находят в результате решения дифференциальных уравнений, описывающих процессы в схеме. Пусть это будут уравнения Кирхгофа:

ii — i 2 — z3 = 0, i1R + i2 R = E, i 2 R — — J i3 dt = 0.

До коммутации

/Ж) = i2(0-) = — = 1(А), i3(0-) = 0, 3 R uC (0-) = i 2 (0-) R = 1 • 50 = 50( В).

После коммутации ii(0+) пр = i 2(0+) пр = 2R = 100 = 1,5( А), uc (0+) пр = i 2(0+) пр R = 1,5 • 50 = 75( В).

Для t (0 ₊ ) уравнения Кирхгофа для двух контуров: ⁱ i⁽⁰ ₊ ) ^R + u c (0 + ) = E , i 2 ⁽⁰ ₊ ) = u C ⁽ 0 ⁺ ) .

R

Так как uC (0 +) = uC (0—) - второе правило коммутации, то uc (0+) св = uc (0+) - uc (0+) пр = 50 - 75 = -25( В);

i i (0 + ) св = i i (0 + ) - i i (0 + ) пр = 2 - 1,5 = 0,5( А );

i 2 (0 + ) св = i 2 (0 + ) - i 2 (0 + ) пр = 1 - 1,5 = - 0,5( А );

i 3 (0 + ) св = i 3 (0 + ) - i ₃(0 + ) пр = 1 - 0 = 1( А ).

Так как duСсв i 3 св = С-С-, dt то duc^ = i3c^ =---1— = 104 (В/с).

dt С   100 - 10 - 6

. -

Каждый ток – сумма принужденной и свободной составляющих - i(0 +)св, умноженной на e т -tt -- -- ii(t) = 1,5 + 0,5e т(А), i2(t) = 1,5-0,5e т(А), i3 (t) = e~ (а), uC(t) = 75 - 25e~ (В).

Получение тех же параметров инженерным методом представлено на рис. 9.

На рисунке использованы данные расчета классическим методом.

i ₂( t ) = А i ₂ • ЭМ1 = 0,5(1 - e ~^т);

i ₂ ( t ) = i ₂ ( t ) + i ₂ ( y ₀) = 0,5(1 - e ~^т) +1 = 1,5 - 0,5 e "^т ( А);

t uC(t) = АuC • ЭМ1 = 25(1 - e т);

t                                    t

U C ( t ) = U C ( t ) + u_C ( y ₀) = 25(1 - e ^T ) + 50 = 75 - 25 e ^T ( В );

i ( t ) = cdu c ^tl = - C Г- 1 ) 25 e "^T = c  1— e "^T = e "^T ( а );

• ³    dt ( tJ         0,5 RC

i 1 ( t ) = i 2 ( t ) + i₃ ( t ) = 1,5 - 0,5 e "^T + e "^T = 1,5 + 0,5 e "^T ( А ).

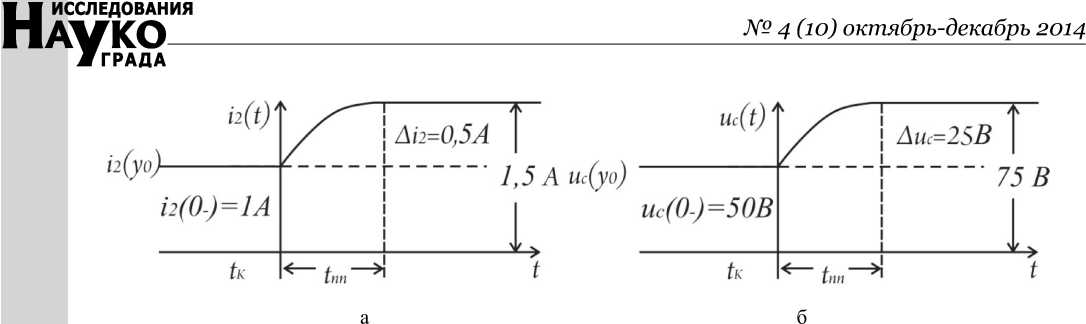
Рис. 9. Графическое представление переходного процесса

Оба решения (классическим и инженерным методами) дают одинаковый результат.

Следует отметить, что при определении i ₃( t ) значение τ = 0,5 RC , так как применение метода эквивалентного генератора относительно нагрузки ( C ) дает R_bh = 0,5 R (оба R оказываются соединенными параллельно).

Сравним анализ процесса, связанного с сохранением заряда (второе правило коммутации), классическим и операторным методами [1] (рис. 10).

С ₂

q 2 пР   С + С   ^C1^UC 10 ^{+ U}C 20 )   ^C2^U 2 ПР ’

U 1 пр   U 2 пр

C i U c 10 ⁺ С 2 U c ²⁰ = 5₀₍ в ).

С 1 ⁺ С 2

Тогда

• - ^-

• U = U, + Ae т.

• ¹       1 ^{п р}

По второму закону коммутации U (0 ) = U ,

C 0

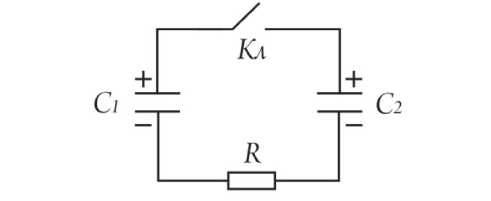
Рис. 10. Схема для сравнения методов

поэтому

U ₁ (0 ₊ ) = 50 + A и

A = U 1 (0 +) - 50 = 50( В ) и t —

U₁(t ) = 50 + 50e ^т .

Л

Аналогично t —

U ₂( t ) = 50 - 25e ^т ( В ),

При начальных U_{C 10} = 100 В, U_{C 20} = 25 В и C 1 = 1 мкФ, C 2 = 2 мкФ, R = 75 Ом необходимо рассчитать напряжение на конденсаторах и ток перезаряда после замыкания ключа Кл.

В установившемся режиме ток равен нулю, то есть аt i (-) = С du- = - C2 dul = - e " ( А ), dt dt

• - _Rc  -R C ₁ C ₂

где т =  - = CTC'

U 1 пр - U 2 пр = 0 или q 1 пр = q 2 пр C ₁ C ₂

По закону сохранения заряда q 10 ⁺ q 20 = ^q 1 пр ⁺ q 2 пр , где

• ^q 10 = ^C 1 ^UC 10 ’ q 20 = ^C2 U C 20 ’

  q 1 пр

  
  

  С 1

  C ₁ + C ₂

  
  

(C1UC10 + UC 20) = C1U1 пр ’ так как конденсаторы оказываются включенными последовательно.

Расчет инженерным методом (рис. 11).

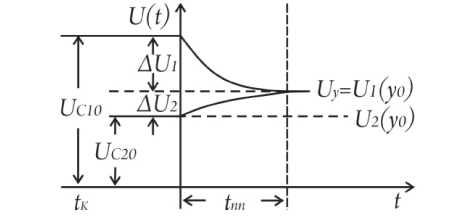
Рис. 11. Для расчета инженерным методом

Оперативный метод анализа переходных процессов в электрических цепях

После замыкания Кл и завершения переходного процесса на обоих конденсаторах установится одинаковое напряжение U_у (рис. 11), относительно которого устанавливают приращения напряжений ( ± Δ U ) на каждом конденсаторе после их перезаряда.

По закону сохранения заряда q10 + q 20 - CUу С2. Uy CU С10 C2UC 20,

_ C i U c 10 + C 2 u_c 20

^uy -     C i + C 2     - ⁵⁰ В ^).

Тогда

1 C 10 у             ^,

• ^{4 u 2 - u} у ^{- Uc 20 - 25(} в ) -

• Ui(t) 4 Hi ЭМ- 50e T (В),

u i ( t ) - u i ( t ) + i ( у 0 ) - 0 e ' 5 + 50(1 e ^т+ В );

- t u2(t) 4 U2 ЭМ1 2-5(1 e T)(В), u 2( t ) u2(t) + u 2(y o)

- 1                   - 1

= 25(1 - e ^T ) + 25 - 50 - 25 e ^T ( В );

Показано, что инженерный метод дает те же результаты, что и традиционные методы, но гораздо оперативнее и «меньшей кровью».

Большой опыт применения традиционных методов показал их широкие возможности, и эти возможности, требующие высокой квалификации специалистов, незаменимы при глубоком изучении «тонких» деталей при исследовании различных процессов в ЭЦ. Когда же речь идет о получении оперативных результатов, оперативном построении математических моделей переходных процессов при экспериментальной отработке, регулировке и испытаниях электронных и электрических устройств, инженерный метод является очень продуктивным.