Оперативный прогноз МПЧ радиотрасс по текущим данным наклонного зондирования ионосферы непрерывным ЛЧМ-сигналом

Одной из важнейших характеристик декаметро-вого радиоканала является максимальная применимая частота (МПЧ) радиотрассы. С одной стороны, МПЧ служит индикатором космической погоды в исследуемом регионе, с другой — значения МПЧ важны с практической точки зрения для организации эффективной работы декаметровых радиотехнических систем радиосвязи. Значения МПЧ определяются параметрами среды (ионосферы) и механизмами распространения радиоволн от излучателя до точки приема. В практике радиосвязи выделяют три вида прогнозов МПЧ: долгосрочный (ДП), краткосроч- ный (КП) и оперативный (ОП) [Иванов, Рябова, 2007]. ДП МПЧ используется для предсказания долгопериодических, регулярных процессов на несколько месяцев вперед на основе модели распространения радиоволн и модели ионосферы как функции пространственных координат, местного времени, сезона и уровня солнечной активности [Vertogradov et al., 2007; Барабашов, Анишин, 2013; Пономарчук и др., 2016]. КП дается на период от нескольких часов до нескольких суток. Прогнозирование состояния ионосферы опирается на индексы, характеризующие поток солнечного излучения (индекс F10.7 или число Вольфа) и возмущенность магнитного поля Земли (индекс Kp или Dst). Существует несколько путей решения задачи. Один из них заключается в использовании эффективных поправок в модели ионосферы, учитывающих вариации МПЧ с изменением солнечной и магнитной активности [Благовещенский, Борисова, 1989; Крашенинников и др., 2008]. Другим является метод, основанный на корреляционной связи МНЧ с ключевыми геоэффективными параметрами межпланетной среды: солнечным ветром и межпланетным магнитным полем [Бархатов и др., 2006]. Однако при такой постановке задачи, несмотря на многолетние исследования, практически значимые методики еще не разработаны. Обусловлено это прежде всего сложностью реакции ионосферы на возмущающие факторы и несоответствия моделей реальным процессам, протекающим в околоземном пространстве в результате воздействия солнечного излучения. Под ОП обычно понимается экстраполяция по времени измеренных ионосферных параметров или значений МПЧ на период от нескольких минут до нескольких часов вперед. Такой прогноз в основном базируется на наличии инерционности временных рядов или выявленных физических закономерностях. Как правило, ОП опирается на данные наземного зондирования (ВЗ, НЗ) ионосферы или данные ГНСС [Бара-башов и др. 2016; Пономарчук и др. 2013; Barabashov et al., 2006; Смирнов и др. 2013]. ОП отличается от ДП главным образом тем, что учитывает текущие данные измерений. В задачах, связанных с анализом временных рядов, под прогнозом понимают экстраполяцию функции, заданной отсчетами.

В настоящее время неотъемлемым элементом современной системы коротковолновой (КВ) связи считается ионосферно-волновая и частотная диспетчерская служба [Ионосферно…, 1998] . Одной из задач, решаемых техническими средствами службы, является оперативное прогнозирование условий радиосвязи, которое заключается в выработке рекомендаций по проведению в ближайшем будущем сеанса связи применительно к выделенному частотному ресурсу и доступным средствам передачи данных. Исходными данными для прогнозирования служат результаты проведенных ранее сеансов зондирования, например сигналами с линейной частотной модуляцией (ЛЧМ). Для практической радиосвязи допустимой считается относительная погрешность определения МПЧ не более 10 %.

Практически можно выделить два вида ОП МПЧ радиотрассы [Рябова, Иванов, 2002]: по временным рядам МПЧ для данной (или близкой) трассы [Куркин и др., 1997; Киселев, 2017] и по модели ионосферы, скорректированной в одной или нескольких точках по текущим данным зондирования ионосферы [Кузьмин, Чалкина, 2013; Арефьев и др., 2016]. Строго говоря, второй вид ОП является не столько прогнозом, сколько способом определения радиофизических параметров трассы в реальном времени.

В работе для оперативного прогноза МПЧ предлагается метод экстраполяции по времени сглаженной по долгосрочному прогнозу последовательности максимальных наблюдаемых частот на заданной трассе. Долгосрочный прогноз МПЧ проводился на базе метода кривых передачи [Кияновский, 1971] с использованием модели ОПЭМИ [Поляков и др., 1986; Dvinskikh, 1988] для коротких трасс и метода нормальных волн [Куркин и др., 1981, Пономарчук и др., 2016] с моделью IRI [Bilitza et al., 2017] для длинных трасс (более 2000 км). Проведено обоснование методики фитирования текущих данных по долгосрочному прогнозу. Апробация метода проводилась по экспериментальным данным, полученным на сети ЛЧМ-зондирования ИСЗФ СО РАН в периоды сильной и слабой солнечной активности.

МЕТОДИКА ОПЕРАТИВНОГО ПРОГНОЗА

Для анализа временных рядов и экстраполяции функций наиболее часто используются разложения по ортогональным функциям (например разложение Фурье) с небольшим количеством слагаемых либо те или иные интерполяционные многочлены. Например, при экстраполяции во времени вперед за основу можно выбрать формулу Ньютона интерполирующего многочлена для равноотстоящих значений независимой переменной [Гельфонд, 1967] . Тогда ОП путем экстраполяции экспериментальных значений за предшествующие моменты времени можно осуществить, ограничиваясь различными степенями представления [Куркин и др., 1997] . Формула Ньютона позволяет осуществить ОП, основываясь только на экспериментальных данных. В работе [Куркин и др., 1993] показано, что МПЧ на разных трассах связаны адиабатическими соотношениями с параметрами ионосферы, поэтому можно предположить, что это справедливо и для одной трассы в разные моменты времени, и, следовательно, можно воспользоваться дополнительной информацией о временной зависимости МПЧ, например, из модельных расчетов по ДП. Предполагая, что этот прогноз качественно верно описывает временную зависимость МПЧ, приращение функции на предыдущем временном интервале можно заменить приращением функции на рассматриваемом интервале, но вычисленным по модели ДП. Опорное значение берется из экспериментальных данных, а последовательные разности на рассматриваемом временном интервале могут быть вычислены как по модельным расчетам, так и по экспериментальным данным.

Такой метод экстраполяции часто встречается в литературе в двух вариантах: либо приращения рассчитываются по модели, либо они еще масштабируются, если модельные значения существенно отличаются от измеренных. Фактически оба метода заключаются в том, что модельная кривая проводится через измеренную точку в первом случае добавлением константы, во втором — умножением на константу. Прогнозируемые точки ищутся на продолжении кривой. При этом можно просто брать значения точек на кривой, а не вычислять их по интерполяционной формуле, которая сама вносит дополнительную погрешность. Оба этих варианта прогноза используют одну измеренную точку, и соответственно, прогноз наследует ее погрешности, хотя и учитывает локальные тренды измеряемой величины, описываемые моделью. Однако он не учитывает локальные тренды измеренных значений, если они отличаются от модели.

В отличие от методик прогноза, в которых только начальная точка взята из эксперимента, а разности берутся по ДП, для небольшого количества точек, начиная с первой, можно использовать регрессию. В качестве регрессионной функции берется перенормированный, или масштабированный ДП, т. е. ДП умножается на такой коэффициент a , чтобы сумма квадратов отклонений ДП от нескольких текущих экспериментальных точек была минимальна. Коэффициент a находится по n точкам экспериментальных данных и данным ДП методом наименьших квадратов:

n

min Z [ f экс ( k ) - af дп ( k ) ] ; k = 1

Z ^f экс ^{( k} ) ^f ДП ^{( k} ) Z f ² n ( ^k )

Далее для прогнозирования используется формула f пр (k +1) = f ДП (k +1) a.

При использовании данной модели прогноза возникает вопрос о количестве точек, которые необходимо выбрать для фитирования измеренных данных моделью ДП, и соответственно, о выборе модели ДП.

Для расчета МПЧ в автоматизированных комплексах выбора рабочих частот радиосвязи предпочтительнее использовать простые инженерные алгоритмы расчета характеристик распространения и модели основных параметров ионосферы без расчета профиля электронной концентрации. Практически ДП МПЧ для ионосферных слоев можно проводить согласно рекомендации Международного союза электросвязи [Методы…, 2016]. На радиотрассах протяженностью до ~2000 км, оборудованных средствами диагностики ионосферы, в качестве метода прогноза ДЧХ и МПЧ целесообразно использовать алгоритм, на основе модифицированного метода кривых передачи [Дэвис, 1973]. Для учета кривизны ионосферы и естественного магнитного поля вводятся поправочные члены [Кияновский, 1971; Копка, Меллер, 1971]. Входной характеристикой для расчета ДЧХ является высотно-частотная характеристика вертикального зондирования ионосферы (ВЧХ) в средней точке радиотрассы. Данная характеристика может быть измерена непосредственно ионозондом в режиме вертикального зондирования или рассчитана по скорректированным прогностическим моделям ионосферы. В ИСЗФ СО РАН на базе полуэмпирической модели ионосферы (ПЭМИ) [Поляков и др., 1986] была разработана оперативная модель параметров ВЧХ (ОПЭМИ) на основе естественных ортогональных функций узловых параметров ВЧХ: fоE, fоF1, fоF2, hF, hF2, hpF, hF1 [Dvin-skikh, 1988].

На протяженных радиотрассах обычно используются алгоритмы расчета траекторных характеристик сигналов [Лукин, Спиридонов, 1971; Vertogradov et al., 2007] , для которых необходимо задание среды распространения — профилей электронной концентрации вдоль трассы распространения. Для прогноза условий распространения декаметровых волн, а также для изучения свойств ионосферы в любой точке пространства Международный комитет по радиосвязи (URSI) рекомендует применять модель IRI [Bilitza et al., 2017] как стандартный вариант модели ионосферы. В данной работе для расчета характеристик распространения на протяженных трассах более 2000 км использовался метод нормальных волн [Куркин и др., 1981] . В рамках комплексного алгоритма, включающего модули расчета глобальной модели ионосферы и характеристик распространения радиоволн в рамках волноводного подхода, реализованы оперативные алгоритмы расчета ДЧХ и МПЧ на трассах наклонного распространения [Пономарчук и др., 2016] . В работе для расчета долгосрочного прогноза МПЧ по методу нормальных волн использовалась модель IRI.

В предлагаемом методе ОП измеренные данные сглаживаются и количество точек, которые следует сглаживать, можно определить исходя из вариативности измеряемой величины. Вариативность МПЧ для данной трассы от дня ко дню в течение месяца согласно литературным данным (например, [Иванов, Рябова, 2007] ) составляет в среднем около 20 %, но может достигать 50 %. При этом среднемесячная медиана ДП может содержать систематическое отклонение, вызванное отличием используемого прогнозного уровня солнечной активности от реального, что приводит к дополнительной погрешности ДП. Но для предложенной методики, когда отрезок реальных данных фитируется отрезком ДП, такие отклонения не являются существенными. Главным фактором является то, что модель корректно учитывает географические и временные (время суток) особенности трассы. Декадные медианы измеренных значений это также учитывают, но при этом из-за смещения терминатора от суток к суткам резкие изменения МПЧ в медиане растягиваются по времени, хотя и не очень сильно, но это вносит дополнительную неслучайную погрешность. На рис. 1 в качестве иллюстрации приведена вариативность МПЧ в каждый момент времени от суток к суткам. Ее среднеквадратичное отклонение (СКО) в течение месяца приведено для двух трасс Хабаровск — Иркутск и Магадан — Иркутск за январь 2014 г.

Видно, что эти вариации составляют 15–20 % и зависят от времени суток. Собственно они и дают погрешность ДП, плюс погрешность, вызванная отли-

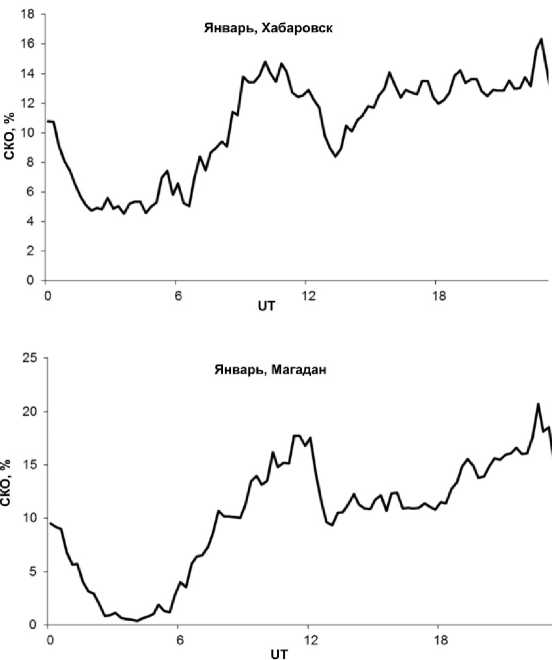
Рис. 1. Среднеквадратичное отклонение МПЧ в течение месяца для двух трасс за январь 2014 г.

чием текущей солнечной и геомагнитной активности, которая также может меняться как в течение суток, так и день ото дня.

На фоне суточного хода МПЧ регистрируются короткопериодные вариации, обусловленные как мелкомасштабными неоднородностями, так и различными волновыми процессами. Знак их может меняться от сеанса к сеансу даже в течение 15 мин, поэтому целесообразно выделить наиболее значимые вариации МПЧ и сгладить вариации, связанные как с мелкомасштабной неоднородной структурой ионосферы, так и с ошибками при определении МПЧ, но с сохранением наиболее существенных вариаций с периодом 1 ч и более.

Для оценки зависимости погрешности прогноза МПЧ по предлагаемой методике от длительности интервалов сглаживания, определяемых скважностью получения данных и числом точек при расчете коэффициента a , были проведены тестовые расчеты СКО ДП от ОП. Использовались экспериментальные данные максимальных наблюдаемых частот (МНЧ), полученных на сети радиотрасс наклонного зондирования ИСЗФ СО РАН [Иванов и др., 2003] . Расчет коэффициента a проводился по 2, 3, 4, 8, 12, 16 точкам, что при 15-минутном интервале зондирования соответствовало интервалам сглаживания 15, 30, 45 мин, 1, 2, 3 и 4 ч соответственно. Видно (рис. 2), что для интервалов заблаговременности менее одного часа преимущество имеют малые предыстории данных. Для больших интервалов сглаживания погрешности возрастают и слабо зависят от предыстории данных для прогноза.

В качестве модели для прогнозирования могут быть выбраны скользящие медианы экспериментальных данных за несколько предыдущих суток. В литературе некоторые авторы рекомендуют интервал усреднения от 5 до 10 сут. Наш анализ по относительно небольшой выборке показал, что результаты прогноза до 3 ч отличаются несущественно (рис. 3), поэтому в используемой методике рассматривается медианная модель ДП.

Различия СКО на рис. 2, 3 обусловлены тем, что для рис. 3 использована меньшая выборка. Таким образом, ожидаемая погрешность ОП по четырем текущим точкам с моделью в виде медианного ДП составляет для 3 ч заблаговременности менее 12 %, а при интервале заблаговременности до 1 ч — около 5 %.

В принципе похожие результаты получаются, если коэффициент подобия вычислять не по наименьшему квадратичному отклонению модели от измеренных значений, а по средневзвешенным значениям нескольких коэффициентов подобия. При этом отсутствуют аргументы в пользу выбора вида среднего. Наш выбор коэффициента подобия соответствует весам a = n 1

k =1

f >кс ^{( k} )     ^f ДП ^{( k} )

f -П ( k 4Z L ft ( - ) J^,

т. е. вес точки увеличивается с ростом величины модельного значения МПЧ, а веса меняются со временем.

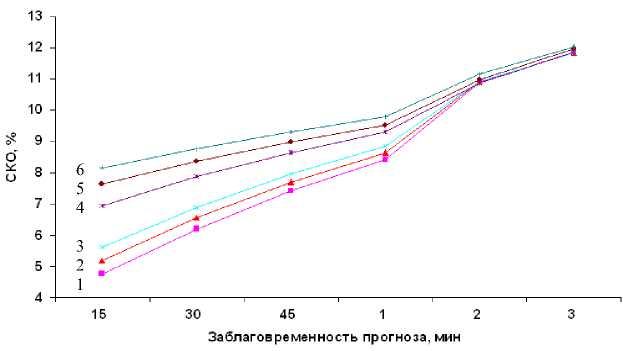
Рис. 2. СКО ОП для различных предысторий для прогноза при 15-мин интервале зондирования: 1 — 2 точки, 2 — 3 точки, 3 —4 точки, 4 — 8 точек, 5 — 12 точек, 6 —16 точек

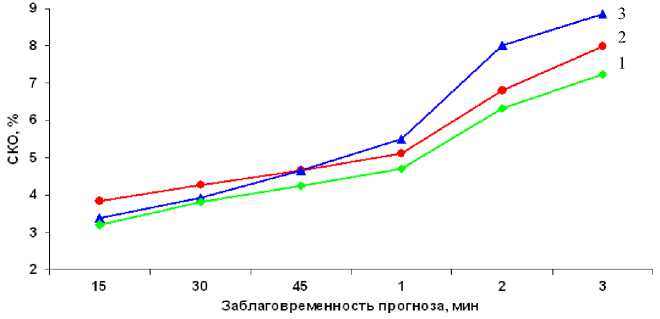
Рис. 3. СКО долгосрочного и ОП прогноза для различных интервалов расчета медианы при 15-мин интервале зондирования: 1 — 5 сут, 2 — 7 сут, 3 — ДП

Погрешность ОП по любой из таких методик будет мало отличаться, поскольку значения коэффициентов будут близки, и мало отличаться от экстраполяции по интерполяционным формулам при сглаживании экспериментальных точек в пределах часа.

АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Для оценки работоспособности разработанного метода были выбраны данные, относящиеся к двум годам с различными индексами солнечной и магнитной активности: 2009 и 2014 г. В течение 2009 г. индекс солнечной активности F 10.7 менялся незначительно — его среднегодовое значение F 10.7 ≈ 70.5 и СКО σ ( F 10.7) ≈ 2.8. В 2014 г. F 10.7 менялся в больших пределах — от 89 до 253. Среднегодовое значение F 10.7 ≈ 146 и σ ( F 10.7) ≈ 27. Среднегодовое значение индекса магнтной активности А р в 2009 г. составило ≈ 4 нТл, что соответствует низкому уровню магнитной активности. В 2014 г. уровень магнитной возмущенности был выше — среднегодовое значение А р ≈ 7.7 нТл, что соответствует в целом возмущенным условиям.

Сравнение качества ОП и ДП с экспериментальными данными проводилось следующим образом: для непрерывного ряда берем наблюдения в течение часа. По этим данным и ДП на тот же период вычисляем коэффициент, на который нужно умножить ДП, чтобы его отклонение от измеренных данных было наименьшим. Затем по умноженному ДП строится прогноз на требуемое время: 15, 30 мин и т. д. Время сдвигается на 15 мин, и процедура повторяется. Вычисляется относительная погрешность между спрогнозированным значением и измеренным. За некоторый промежуток времени (как правило, один месяц) рассчитывается СКО этой погрешности, т. е. СКО прогноза от измерений (корень из среднего квадрата отклонений).

Для сравнения качества ОП и ДП были выбраны экспериментальные данные МПЧ на трассах Хабаровск — Иркутск, Магадан — Иркутск и Норильск — Иркутск для различных сезонов при высокой и низкой солнечной активности.

На рис. 4–6 для примера приведены графики суточных вариаций МПЧ для трасс Хабаровск — Иркутск за январь 2014 г., Магадан — Иркутск за апрель 2009 и январь 2014 г., Норильск — Иркутск за сентябрь 2009 и январь 2014 г. соответственно. На рис. 4–6 также показаны результаты ДП и ОП на 15 и 30 мин в выбранные периоды наблюдений.

В табл. 1–5 приведены СКО ДП и ОП с заблаговременностью 15, 30 мин и 1 ч и количество точек прогноза, отклоняющихся от измеренных не более чем на 10 %.

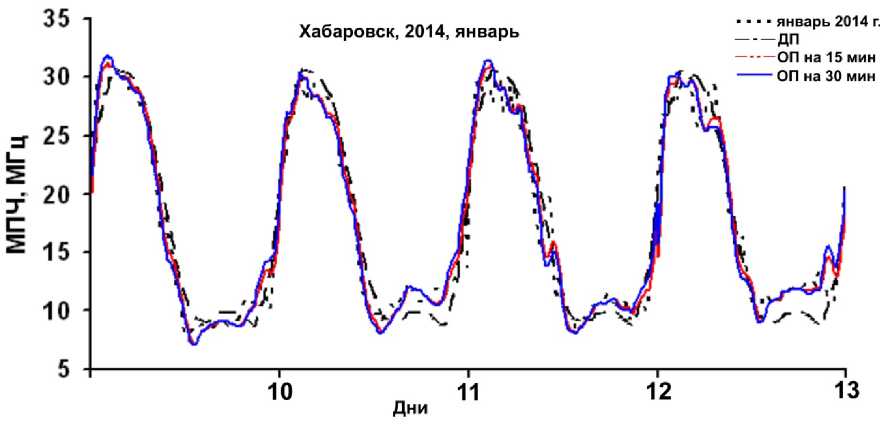
Рис. 4. Суточный ход реальных данных на трассе Хабаровск — Иркутск, январь 2014 г.

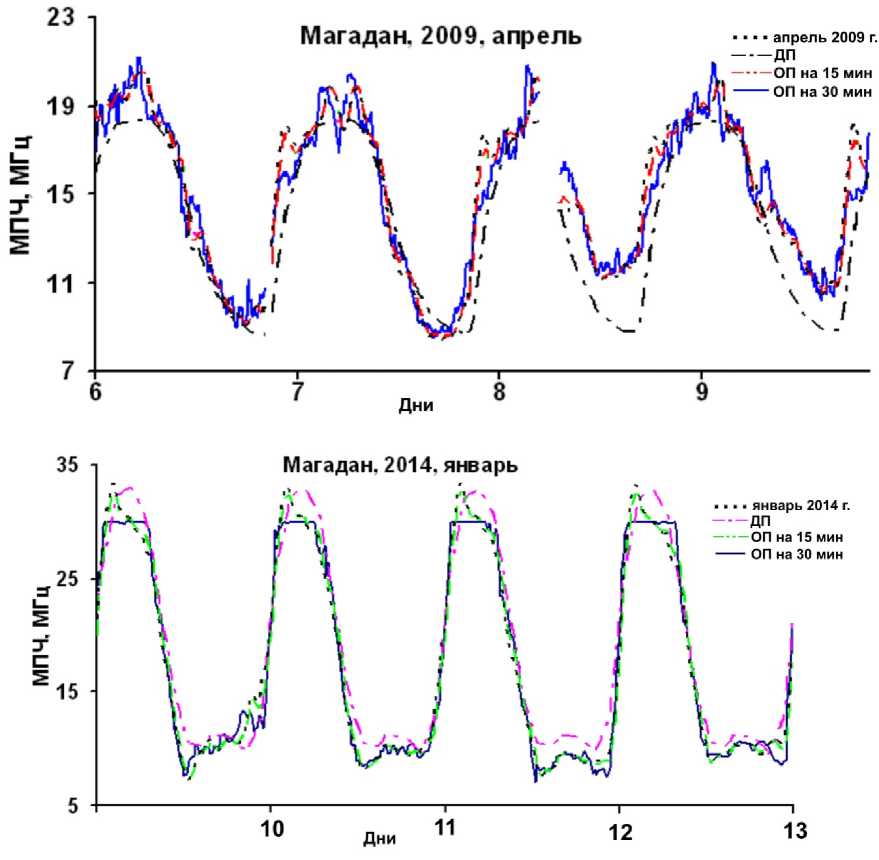
Рис. 5. Суточный ход реальных данных на трассе Магадан — Иркутск: апрель 2009 и январь 2014 г.

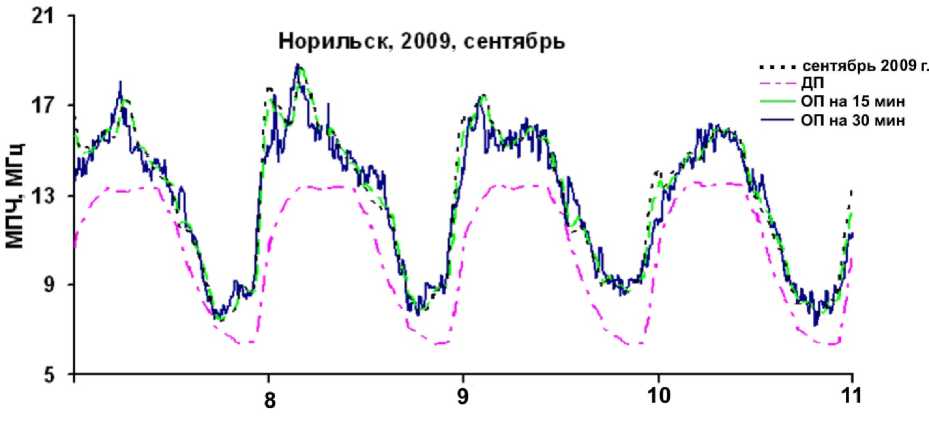
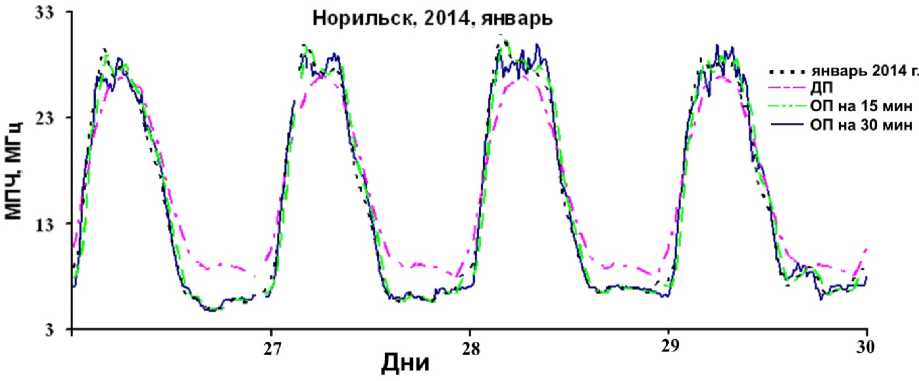
Рис. 6. Суточный ход реальных данных на трассе Норильск — Иркутск: сентябрь 2009 и январь 2014 г.

Таблица 1

СКО ДП и ОП с заблаговременностью 15, 30 мин и 1 ч для трассы Хабаровск — Иркутск (2014 г.)

	ДП, %	ОП на 15мин, %	ОП на 30 мин, %	ОП на 1 ч, %
январь	13.1	9.6	10.7	16.3
март	19.7	4.68	5.74	7.3
июнь	19.2	5.6	6.96	9.3

Доля точек, отличающихся менее чем на 10 %

	ОП на 15 мин, %	ОП на 30 мин, %	ОП на 45 мин, %	ОП на 1 ч, %
январь	78.6	75.8	67.4	61.5
март	96.2	92.3	87.9	83.8
июнь	92.2	82.1	74.8	70.5

Таблица 2

СКО ДП и ОП с заблаговременностью 15, 30 мин и 1 ч для трассы Норильск — Иркутск (2009 г.)

	ДП, %	ОП на 15 мин, %	ОП на 30 мин, %	ОП на 1 ч, %
январь	35.8	11.34	14.3	19.9
февраль	29.3	12.99	16.5	22.5
сентябрь	23.4	6.13	7.22	8.9

Доля точек, отличающихся менее чем на 10%

	ОП на 15 мин, %	ОП на 30 мин, %	ОП на 45 мин, %	ОП на 1 ч, %
январь	66.9	59.25	53.3	47.9
февраль	68	60.9	55.45	49.9
сентябрь	90.56	85.79	80.84	77.04

Таблица 3

СКО ДП и ОП с заблаговременностью 15, 30 мин и 1 ч для трассы Норильск — Иркутск (2014 г.)

	ДП, %	ОП на 15 мин, %	ОП на 30 мин, %	ОП на 1 ч, %
январь	23.02	9.3	11.66	15.46
апрель	15.49	6.36	8.03	10.97
июнь	22.44	5.2	6.3	7.6

Доля точек, отличающихся менее чем на 10 %

	ОП на 15 мин, %	ОП на 30 мин, %	ОП на 45 мин, %	ОП на 1 ч, %
январь	75.9	66.8	59.4	53.2
апрель	89.5	84.7	80.2	74.9
июнь	94.8	91.4	87.87	85.1

Таблица 4

СКО ДП и ОП с заблаговременностью 15, 30 мин и 1 ч для трассы Магадан — Иркутск (2009 г.)

	ДП, %	ОП на15 мин, %	ОП на 30 мин, %	ОП на 1 ч, %
январь	26.18	10.9	13.64	18.41
февраль	19.25	10.5	13.2	17.5
апрель	13.46	5.75	6.95	8.9

Доля точек. отклоняющихся менее чем на 10 %

	ОП на 15 мин, %	ОП на 30 мин, %	ОП на 45 мин, %	ОП на 1 ч, %
январь	73.2	64.5	58.6	54.15
февраль	78.44	71.03	64.6	60.2
апрель	90.27	84.6	81.1	77.7

Таблица 5

СКО ДП и ОП с заблаговременностью 15, 30 мин и 1 ч для трассы Магадан — Иркутск (2014 г.)

	ДП, %	ОП на15 мин, %	ОП на 30 мин, %	ОП на 1 ч, %
январь	12.7	9.4	14.5	15.3
март	29.7	4.3	5.4	7.2
июнь	15.1	6.7	8.2	11

Количество точек, ОП которых отклоняется менее чем на 10 %

	ОП на 15 мин, %	ОП на 30 мин, %	ОП на 45 мин, %	ОП на 1 ч, %
январь	76.9	68.2	62.2	57.9
март	97.2	93.4	88.45	82.6
июнь	88	80	73.2	67.6

Таблица 6

Средние отклонения и СКО прогнозных значений от реальных для трассы Хабаровск — Иркутск, март 2014 г.

Интервал заблаговременности	Среднее значение, %				СКО, %				%, от –10 % до +10 %
	1т	2т	3т	4т	1т	2т	3т	4т	1т	2т	3т	4т
15 мин	0.10	0.13	0.17	0.21	4.58	4.76	5.19	5.63	96	98	96	96
30 мин	0.18	0.22	0.26	0.29	5.96	6.19	6.55	6.89	92	95	94	91
45 мин	0.28	0.31	0.34	0.37	7.64	7.41	7.69	7.96	87	92	90	90
1 ч	0.36	0.39	0.42	0.45	8.30	8.42	8.64	8.84	82	88	87	88
2 ч		0.63	0.64	0.65		10.90	10.91	10.91		79	81	81
3 ч		0.73	0.74	0.75		11.86	11.83	11.83		73	73	74

Приведенные данные показывают, что точность ОП на 15 мин наилучшая и существенно превышает точность ДП. Чем больше заблаговременность прогноза, тем меньше точность ОП, но для прогноза 1 и даже 2 ч погрешность ОП меньше, чем ДП. Количественные показатели существенно зависят от трассы и сезона, но в любой ситуации СКО ОП от измеренных значений не превосходит 9 %, в большинстве случаев — меньше 5 %. Количество точек, отклоняющихся менее чем на 10 % при 15-мин прогнозе, как правило. превосходит 70 %. а в ряде случаев и 90 %. Исключения составляют зимние месяцы, где погрешности ДП и ОП выше, особенно на меридиональной трассе Норильск — Иркутск.

В табл. 6 приведены средние отклонения и СКО прогнозных значений от реальных для трассы Хабаровск — Иркутск для марта 2014 г. и промежутка времени, когда реальные МНЧ не превышают предельную частоту зондирования 30 МГц (8 — 23:45 UT).

Таким образом, погрешность ДП существенно больше погрешности ОП, но в качестве модели, используемой в предложенной методике оперативного прогнозирования, медианный ДП работает вполне удовлетворительно.

ЗАКЛЮЧЕНИЕ

Представлена методика оперативного прогнозирования МПЧ, основанная на экстраполяции по времени последовательности МНЧ на заданной трассе с коррекцией по ДП. Проведен анализ методики по данным МНЧ на сети трасс ИСЗФ СО РАН для различных сезонов и уровней солнечной активности. Выявлено существенное улучшение качества прогноза по сравнению с ДП при интервалах заблаговременности ОП от 15 до 30 мин. Доля сеансов, в котором погрешность оперативного прогноза не превышает 10 %, составляет при 15-мин интервале заблаговременности от 67 до 96 % в зависимости от сезона и ориентации радиотрасс.

Авторы благодарят Н.М. Полех за предоставленные данные по ионосферной обстановке на анализируемые периоды и В.А. Иванову за помощь в обработке данных ЛЧМ-зондирования.

Работа выполнена в рамках базового финансирования программы ФНИ II.12. Результаты получены с использованием оборудования Центра коллективного пользования «Ангара»,