Описание форм птичьих яиц с помощью геометрических эталонов

Введение. Птичье яйцо как биологическое тело с геометрической точки зрения устроено довольно просто. Однако специфика форм яиц у разных видов птиц порождает определенные трудности в процессе их описания. В полевых условиях непосредственно с яйца можно снять легко только два промера: диаметр и длину. Их, безусловно, недостаточно для полноценного описания формы. Дополнительные параметры можно получить или из плоскостной проекции (светокопии, фотографии) (Romanoff, Romanoff, 1949; Костин, 1977; Мянд, 1988; Fuhrer-Nagy, 2002), или же осуществить замеры при помощи специально изготовленных устройств (Preston, 1953). С появлением цифровой фотографии и возможностей их компьютерной обработки проблема снятия дополнительных параметров стала легко решаемой. В литературе появилось немало работ, посвященных этим методикам описания яиц (Makatsch, 1976; Anderson, 1978; Todd, Smart, 1984; Barta, Szekely, 1997; Baker, 2002; Митяй, 2003, 2008; Monus, Barta, 2005; Narushin, 2005; Bridge et al., 2007). Упомянутые методики все же не

Вестник ТвГУ. Серия "Биология и экология". 2014. № 1 разрешили проблем, связанных с названием, классификацией форм яиц, а также возможностью сравнения ооморфометрических данных, публикуемых различными авторами.

В литературе нет единого подхода в отношении названий форм яиц. Они или малоинформативны, типа «яйцо с ярко выраженным тупым и острым концом», или тавтологичны - «овоидный тип формы яйца». Не лишены недостатков и названия по подобию с геометрическими фигурами (сферические, эллипсоидные, овальные) или другими телами (каплевидные, грушевидные, юловидные). Зачастую это подобие очень условно, поскольку в реальных яйцах на разных полюсах проявляются разные фигуры. Не существует также единства в выборе количества базовых фигур. У разных авторов их: три (Makatsch, 1976; Климов, 1993), четыре (Preston, 1953; Narushin, 2005), пять (Gotman, Jablonski, 1972), восемь (Walters, 1994), десять (Schonwetter, 1985; Barta, Szekely, 1997). К тому же, предлагаемые фигуры рассматриваются вне единства и количественных характеристик.

В связи с этим, обобщение и сравнение данных разных авторов в значительной степени затруднено. На наш взгляд, проблема может быть решена при наличии комплексной системы описания форм яиц, включающей в себя название, геометрическую модель (фигуру) и ее количественные параметры. Другими словами, необходима общепринятая методика в виде эталонов форм, используя которые исследователи работали бы в едином русле. Обоснованию и изложению подобной методики посвящена данная статья.

Методика. Материалом для исследования послужили 16494 яиц 800 видов птиц Северо-Западной Палеарктики, относящихся к 20 отрядам.

В качестве базовой модели автором использована фигура, которая в начертательной геометрии и инженерной графике называется овоидом или асимметрическим овалом (рис. 1).

Согласно одному из определений, овоид является плоской, замкнутой, выпуклой, гладкой кривой, состоящей из взаимно сопрягающихся дуг окружностей разных радиусов. Характерными признаками этой кривой является наличие одной оси симметрии и не менее четырех вершин. В реальных яйцах этим вершинам соответствуют зоны: инфундибулярная (место размещения воздушной камеры), клоакальная (противоположная, более заостренная - место локализации аллантоиса) и две латеральные, являющиеся боками интерполярной зоны, в которой размещается зародыш. На плоскостной проекции каждая из этих зон очерчена одноименными дугами, сопряжение которых и образует овоид.

Для описания и классификации форм яиц автор использовал модель составного овоида, согласно которой все разнообразие форм получается путем составления (комбинации, сопряжения, плавного перехода) дуг адекватных кривизне зон овоида. Для каждой из форм строилась геометрическая фигура, наглядно отражающая отношения клоакальной, инфундибулярной дуг, длины и диаметра овоида. Количественное описание овоидов осуществляли с помощью семи индексов формы: традиционный индекс удлиненности - Iei= L/D и шесть индексов, предложенных нами: (112=ц/В; Iiz=ri/D; Icz=rc/D; Iipz=L-(й+Гс) lel^Hz+Icz), las Iiz~Icz O"i-l*c)/D, Icom (гс+1ф2)(1|р2+Г})/1{р2К, ГДС. ф2, Icz, 1ц, las, Icom, Lpz - индексы инфундибулярной, клоакальной, латеральной зон, асимметрии, интерполярный и индекс комплементарности; р, гС) р -радиусы дуг; L -длина; D - диаметр. Последний индекс отражает степень сбалансированности (гармоничности) инфундибулярного (р) и клоакального (гс) радиусов с длиной овоида. В конформной геометрии этот показатель называется двойным отношением или вурфом. Для описания форм яиц этот индекс нами предлагается впервые. Значения, приближающиеся к единице, характеризуют яйца с минимальным радиусом клоакальной зоны. Величины, приближающиеся к 1,333, свидетельствуют, что длина яйца состоит из трех равных отрезков, два из которых являются радиусами полярных зон. Показатели, уходящие за пределы 1,333, характеризуют яйца с большими радиусами клоакальных дуг.

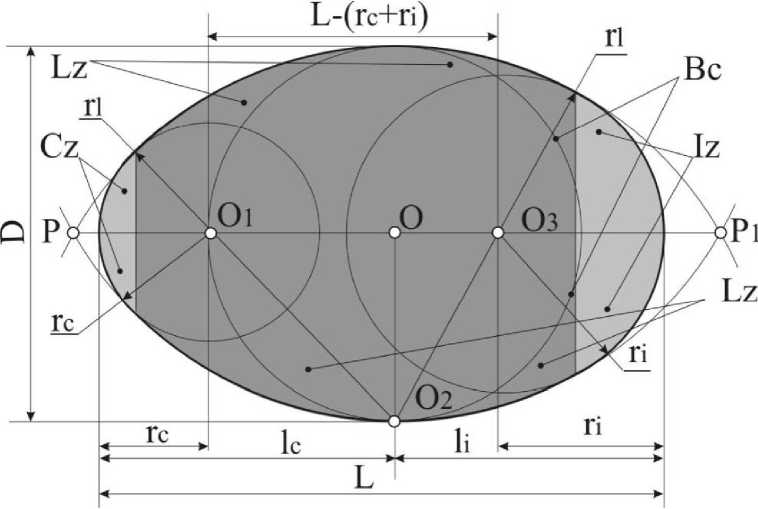
Рис. 1 . Обобщенная схема овоида и варианты снятия параметров: 0-0з - центры сопрягаемых дуг; Р, Pi - точки пересечения латеральных дуг; В_с - базовая окружность; Iz, Lz, Cz - инфундибулярная, латеральная и клоакальная зоны овоида и их радиусы: г,, ц, r_c; D - диаметр; L - длина;

Н, 1с - инфундибулярная и клоакальная части длины

Исходные параметры, длина (L) и диаметр (D), реальных яиц измеряли штангенциркулем с точностью до 0,1 мм. Замеры необходимых радиусов дуг окружностей выполняли по цифровым

Вестник ТвГУ. Серия "Биология и экология". 2014. № 1

фотографиям с помощью компьютерных программ, разработанных Б. Троценко и С. Шелестюком. Им автор выражает искреннюю благодарность.

Результаты и обсуждение. Яйца большинства птиц, на первый взгляд, кажутся весьма однообразными. Различия становятся явными при сравнении параметров их форм между собой. Простое сравнение плоскостных проекций яиц показывает, что у одних полярные зоны одинаковы, а у других разные. На основании этого все разнообразие форм яиц можно разделить на две группы: симметрические и асимметрические (рис. 2).

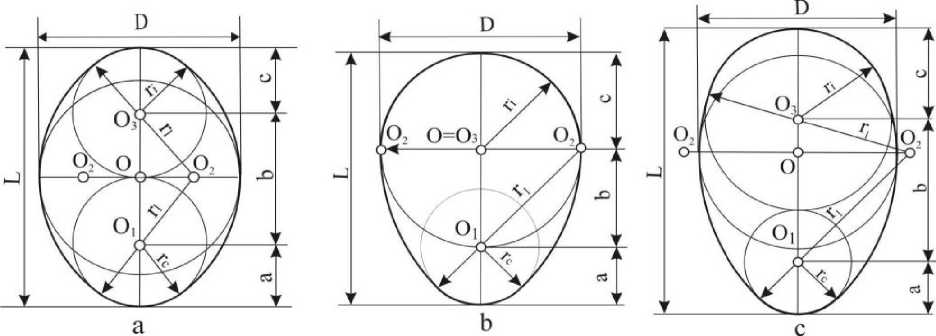
Рис. 2. Формы яиц по конфигурации полярных зон: а) симметрические; Ь, с) асимметрические

Для классификации форм яиц в качестве исходной (базовой) геометрической фигуры подходит овоид, в котором одна часть является половиной окружности, а другая - половиной овала (рис. 2, Ь). Исходя из этого, все фигуры, инфундибулярный радиус которых лежит в пределах половины базового диаметра (ц=0,5-0,499 D), получают название овоидов. Они составляют 21,3% от указанного выше количества яиц (п=16490). Учитывая то, что инфундибулярный радиус константный, дальнейшее разграничение форм осуществляется по отличиям латеральных и клоакальных радиусов. Все разнообразие форм возникает в пространстве, ограниченном двумя латеральными дугами, которые пересекаются в точках Р и Pi (рис. 3).

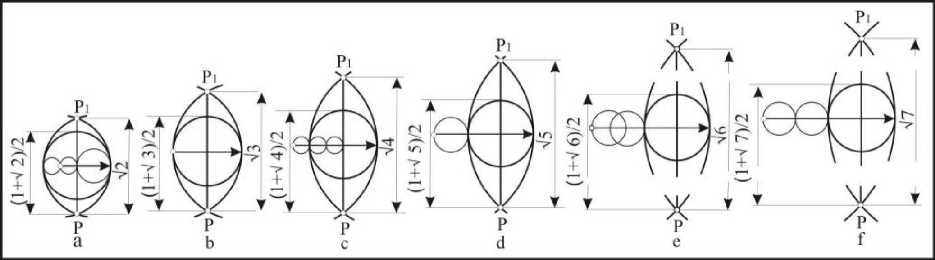
Рис. 3 . Интервалы и взаимосвязь латеральних дуг с диаметром и длиной овоидов

Взаимосвязь радиусов латеральных дуг и расстояний между точками их пересечения выражается следующим уравнением: PPi= V(4Dri - D2). В соответствии с ним, радиусам латеральных дуг 0,75D; 1,OD; 1,25D; 1,5D; 1,75D; 2,0D отвечают расстояния, равные корням квадратным из чисел 2, 3, 4, 5, б и 7. В каждом из упомянутых случаев радиусы сопрягающих дуг разные, что отражается на конфигурации клоакальной зоны. Сопряжение латеральных дуг осуществляется клоакальной окружностью таким образом, что его противоположная от места сопряжения часть может занимать различное положение на продольной оси профиля в зависимости от величины диаметра (рис. 4).

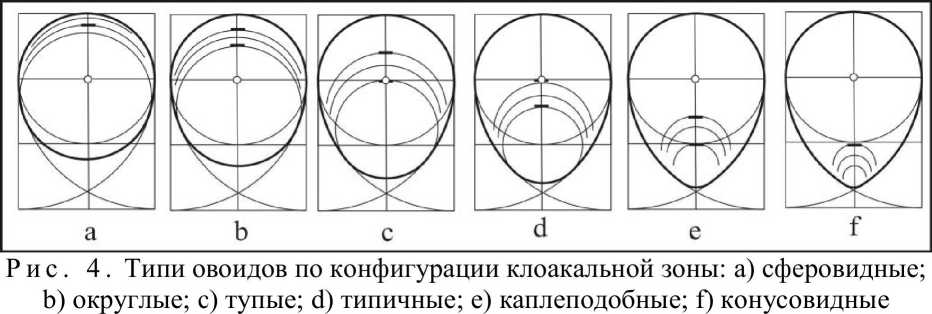
Если продольную ось условно разбить на интервалы, то мы получим возможность количественно выражать радиусы клоакальных дуг через половины отрезков длины овоида: L-0,125; L-0,25; L-0,5; L-0,75; L-D; (L-D)/2; (L-D)/4. Исходя из этого, было выделено шесть типов овоидов, названия которым были даны в соответствии с положением клоакальной окружности: сферовидные, округлые, тупые, типичные, каплевидные и конусовидные. Каждая из этих форм внутри себя имеет различные радиусы клоакальной дуги. Поэтому вышеупомянутые овоиды получили дополнительные названия: крупнорадиусные, среднерадиусные и мелкорадиусные. В зависимости от того, в пределах каких латеральных дуг происходит сопряжение, длина овоидов бывает различной. Это дало еще пять дополнительных названий: короткие, укороченные, нормальные, удлиненные и длинные. Приняв во внимание упомянутые геометрические особенности овоида, мы разработали систему из 80 базовых овоидов, объединенных в 6 типов.

Первый тип включает формы, приближающиеся к сфере. Они получили название сфероподобные. Их клоакальные окружности имеют диаметры в пределах D>d_c>L-0,125D (рис. 5).

Индекс удлиненности таких яиц приближается к единице: 1,0<1е1<1,09. У птиц таких форм очень мало, около 0,2% (п=3498). Они встречаются отрядах Galliformes, Piciformes и Passeriformes.

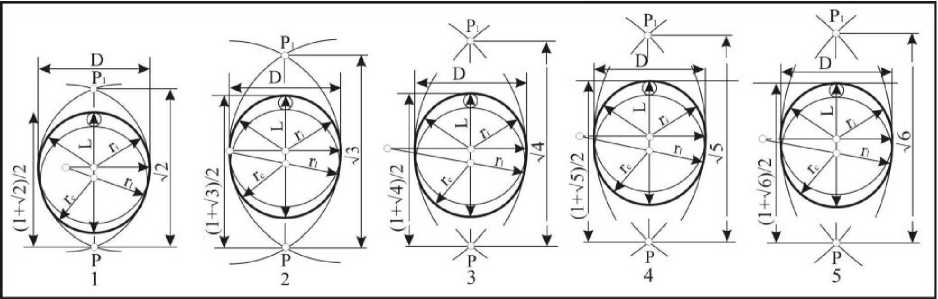
Рис. 5 . Сфероподобные овоиды

Второй тип объединяет формы с диаметрами в пределах L-0,125D>d_e>L-0,375D (рис. 6). Они получили условное название округлые: крупнорадиусные (6-10), среднерадиусные (11-15) и мелкорадиусные (16-20) с дополнительными характеристиками: короткие (6, 11, 16), укороченные (7, 12, 17), нормальные (8, 13, 18), удлиненные (9, 14, 19) длинные (10, 15, 20). Индекс удлиненности: 1,091<1е1< 1,287. Встречаются указанные формы в 4,0% случаев представителей отрядов, приведенных для первого типа (рис. 6).

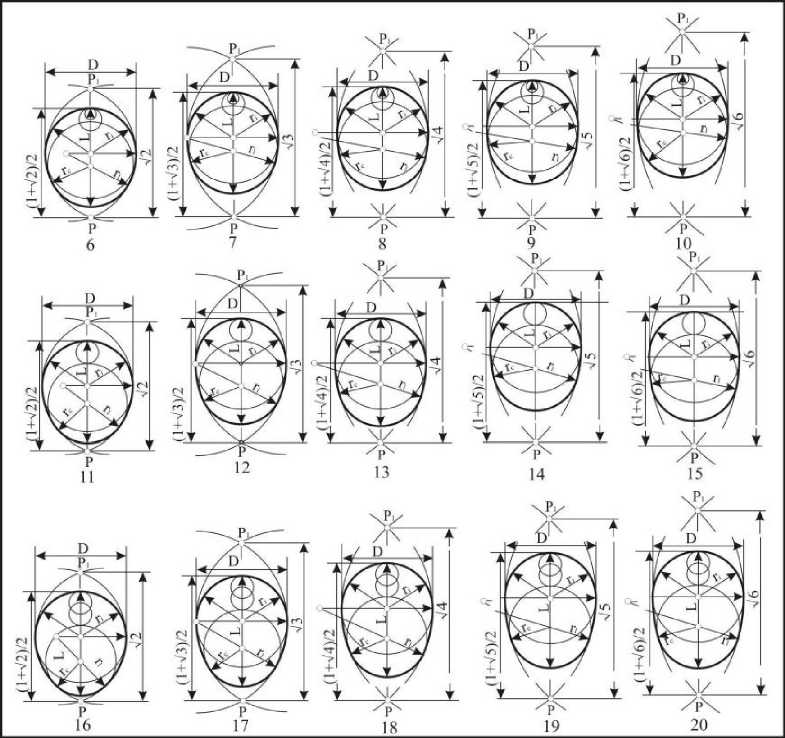
Рис. 6. Округлые овоиды

Третий тип, объединяющий формы с диаметрами в пределах L-0,375D>d_c>L-0,625D (рис. 7), представлен формами, названными нами тупыми овоидами. Каждая из этих форм, как и в предыдущем случае, делится на крупно-, средне- и мелкорадиусные (21-25, 26-31, 32-36), и, соответственно, короткие (21, 26, 32), укороченные (22, 27, 33), нормальные (23, 28, 34), удлиненные (24, 30, 35) и длинные (25, 31, 36). Индекс удлиненности яиц третьего типа находится в пределах 1,146<1е1<1,4. Упомянутые формы встречаются в 40,9% случаев у представителей из отрядов Galliformes, Charadriiformes, Falconifonnes и Piciformes Passeriformes. Незначительное их число отмечено у Gruiformes и Coraciiformes.

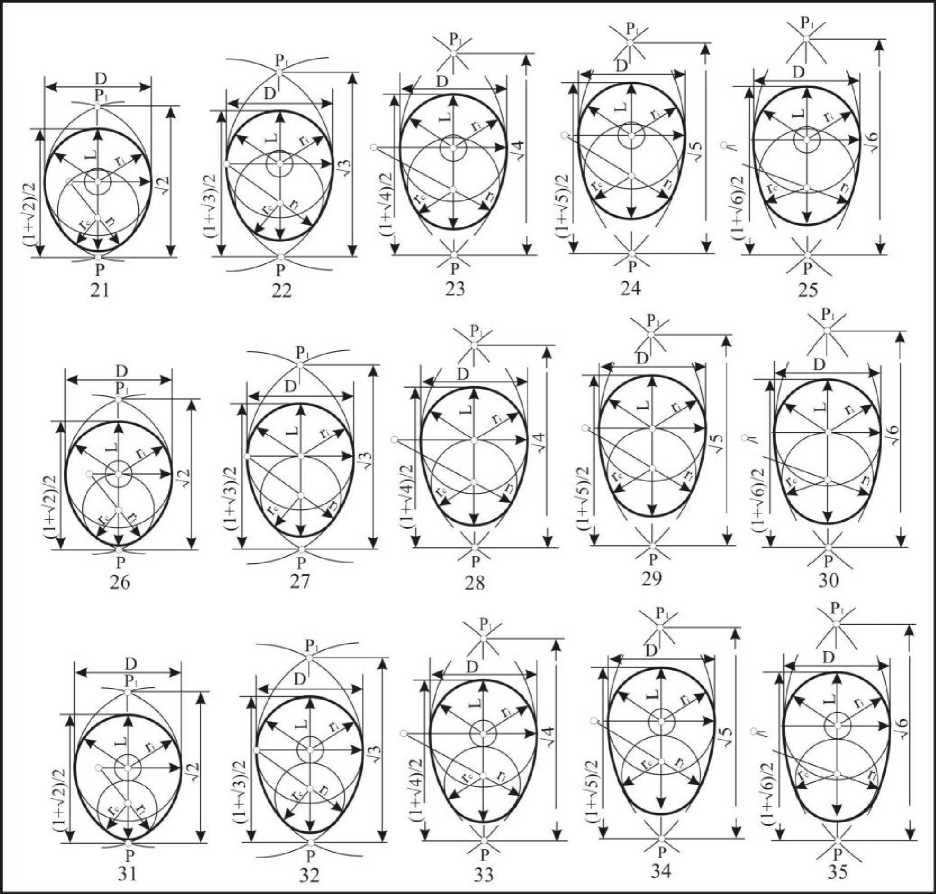
Рис. 7 . Тупые овоиды

Четвертый тип включает в себя типичные овоиды - формы с клоакальными окружностями в пределах L-0,625D>d_e>L-0,75D (рис. 8). Они подразделяются на: крупнорадиусные (36-40), среднерадиусные (41-45) и мелкорадиусные (46-50). По длине подразделение

Вестник ТвГУ. Серия "Биология и экология". 2014. № 1 осуществляется на: короткие (36, 41, 46), укороченные (37, 42, 47), нормальные (38, 43, 48), удлиненные (39, 44, 49) и длинные (40, 45, 50). Индекс удлиненности тупых овоидов находится в пределах 1,146<1е1<1,4. Упомянутые формы встречаются в 41,2% случаев у представителей отрядов Anseriformes, Charadriiformes, Falconiformes, Galliformes, Gruiformes, Picifomies и Passeriformes.

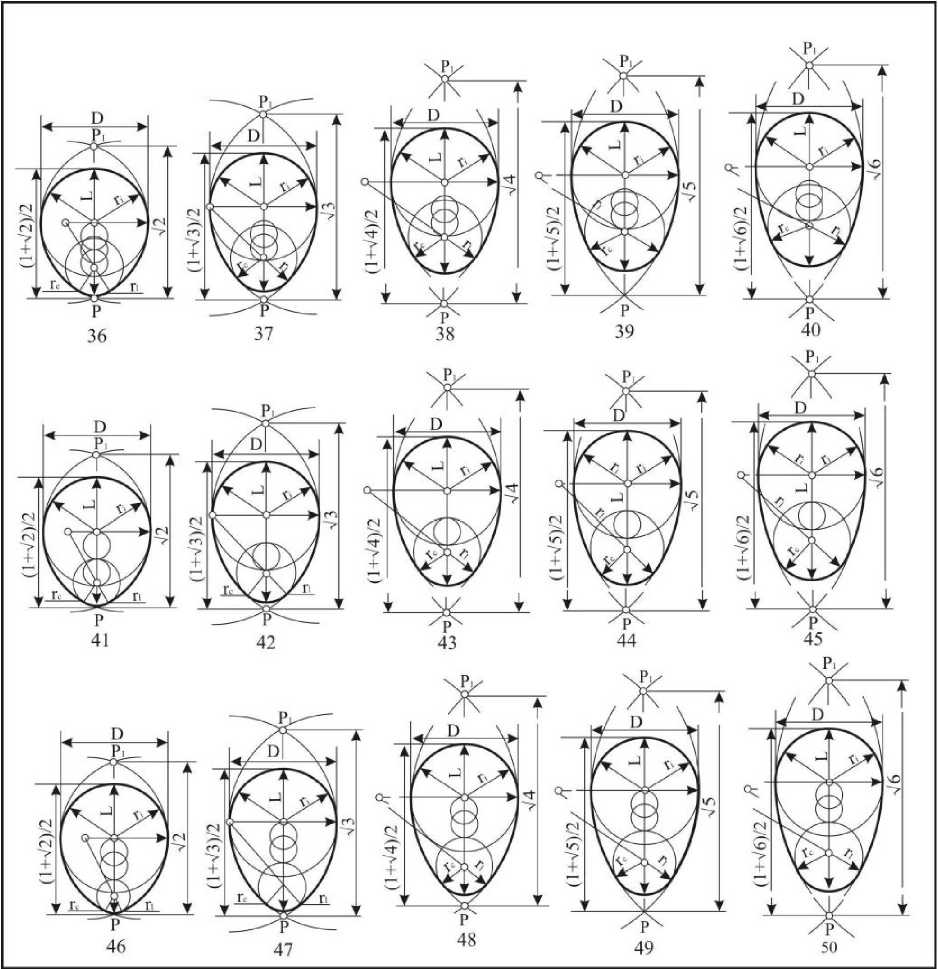
Рис. 8 . Типичные овоиды

Пятый тип: клоакальные радиусы находятся в пределах L-0,75D>d_c>L-l,125D (рис. 9). Эти формы получили название каплевидных овоидов. Они подразделяются на: крупнорадиусные (5155), среднерадиусные (56-60) и мелкорадиусные (61-65). По длине подразделение осуществляется на: короткие (51, 56, 61), укороченные (52, 57, 62), нормальные (53, 58, 63), удлиненные (54, 59, 64) и длинные (55, 60, 65). Индекс удлиненности этих яиц находится в

Вестник ТвГУ. Серия "Биология и экология". 2014. № 1

пред елах,323<1е1< 1,643. Каплевидные овоиды встречаются в 48,2% случаев у представителей двух отрядов, Charadriiformes и Passerifonnes.

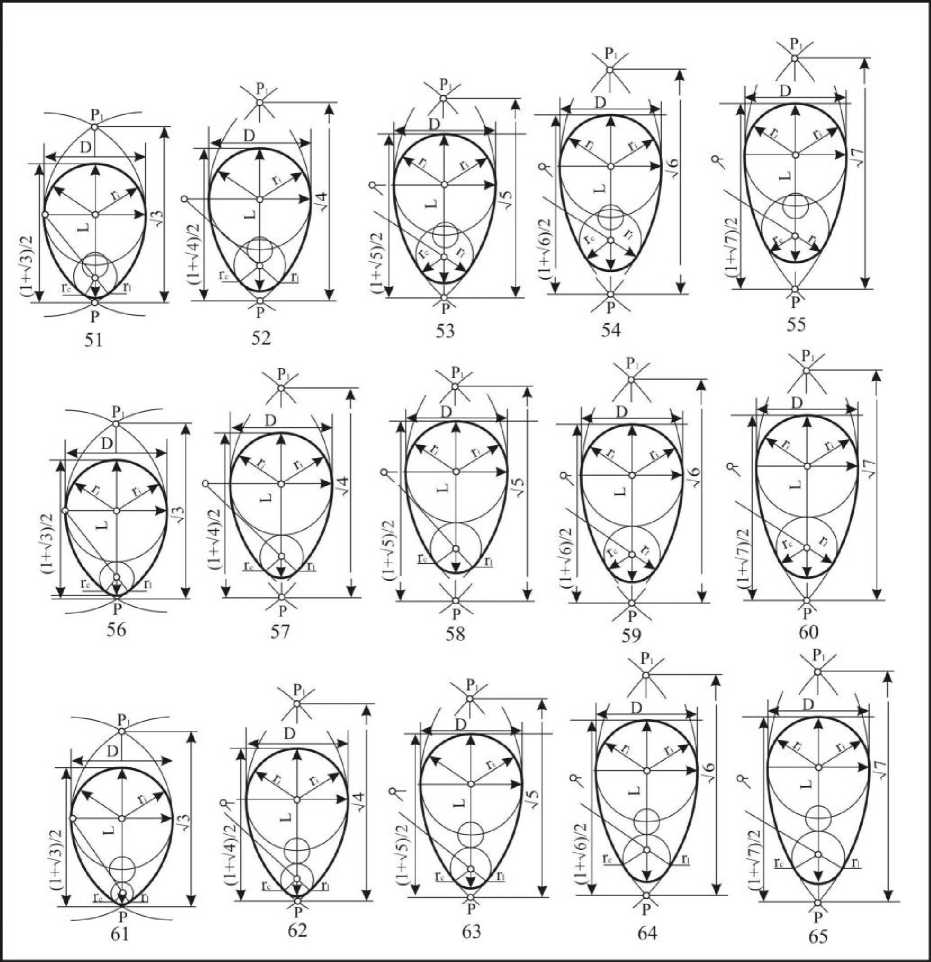
Рис. 9 . Каплевидные овоиды

Шестой тип : клоакальные окружности находятся L-0,125D>d_c>L-2,0D (рис. 10). Они получили название конусовидных овоидов: крупнорадиусных (66-70), среднерадиусных (71-75) и мелкорадиусных (76-80). По длине овоиды шестрого типа подразделяются на: короткие (66, 71, 76), укороченные (67, 72, 77) нормальные (68, 73, 78), удлиненные (69, 74, 79) и длинные (70, 75, 80). Индекс удлиненности этих яиц находится в пределах 1,449<1е1<1,745. Конусовидные овоиды встречаются в 9,3% случаев у представителей отряда Charadriiformes.

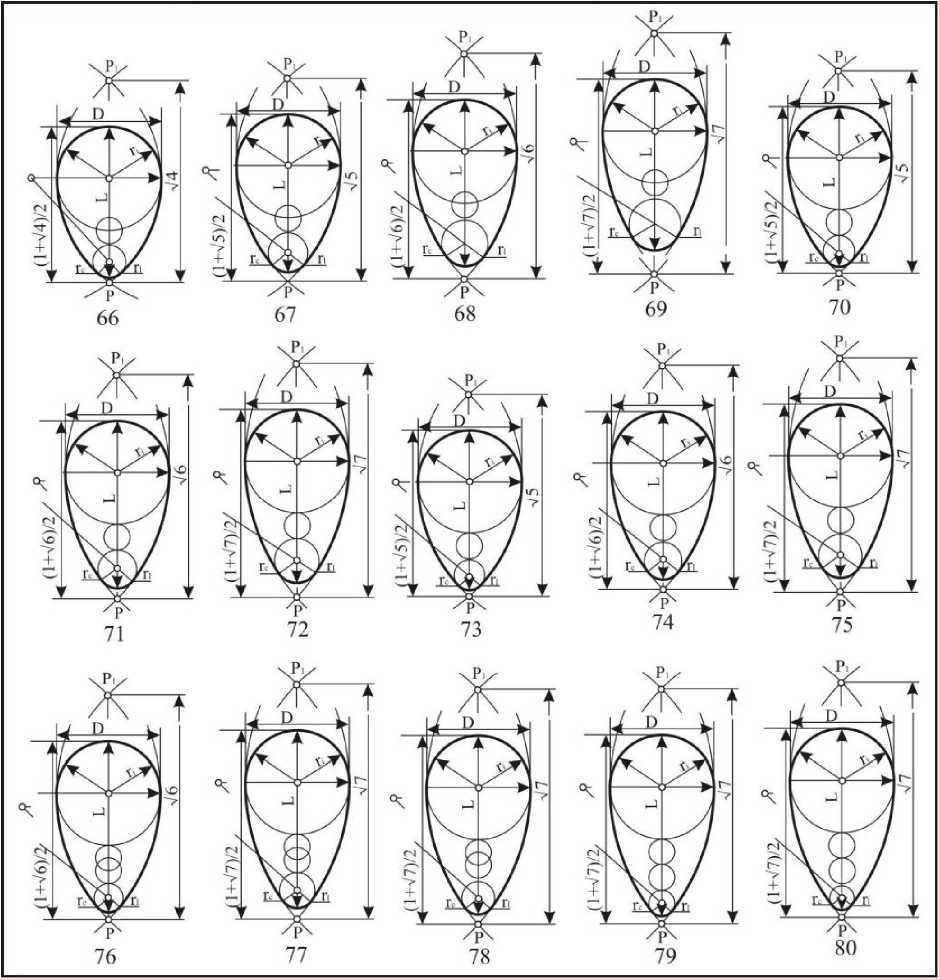
Рис. 10. Конусовидные овоиды

Вышеприведенные геометрические овоиды-эталоны имеют фиксированные (индивидуальные) характеристики, выраженные в виде индесов клоакальной и латеральной зон, а также индексов удлинености, комплементарности, асиметрии и интерполярности. Получившие порядковые номера, названия и характеристики, указанные эталоны предлагаются нами в качестве базовых при описании формы яйца (табл. 1).

Таблица 1

Названия и параметры базовых овоидов-эталонов

№	Название эталона	Icz	Ilz	lei	Icom	las	lipi
Сферовидные овоиды:
1	короткие	0,480	0,75	1,083	3,152	0,020	0,103
2	укороченные	0,487	1,00	1,098	2,987	0,013	0,112
3	нормальные	0,490	1,25	1,111	2,822	0,010	0,121
4	удлиненные	0,493	1,50	1,115	2,803	0,007	0,123
5	длинные	0,494	1,75	1,116	2,814	0,006	0,122
Округлые овоиды
6	Крупнорадиусные: короткие	0,478	0,75	1,091	2,806	0,022	0,120
7	укороченные	0,488	1,00	1,108	2,826	0,012	0,121
8	нормальные	0,490	1,25	1,112	2,797	0,010	0,123
9	удлиненные	0,491	1,50	1,140	2,439	0,009	0,150
10	длинные	0,493	1,75	1,143	2,432	0,007	0,151
11	Среднерадиусные: короткие	0,437	0,75	1,125	2,029	0,063	0,189
12	укороченные	0,459	1,00	1,169	1,935	0,041	0,210
13	нормальные	0,468	1,25	1,190	1,883	0,032	0,223
14	удлиненные	0,473	1,50	1,200	1,868	0,027	0,227
15	длинные	0,477	1,75	1,207	1,856	0,023	0,231
16	Мелкорадиусные: короткие	0,387	0,75	1,151	1,637	0,113	0,264
17	укороченные	0,423	1,00	1,218	1,589	0,077	0,295
18	нормальные	0,441	1,25	1,256	1,556	0,059	0,316
19	удлиненные	0,449	1,50	1,271	1,549	0,051	0,322
20	длинные	0,456	1,75	1,287	1,535	0,044	0,331
Тупые овоиды
21	Крупнорадиусные: короткие	0,382	0,75	1,146	1,629	0,118	0,265
22	укороченные	0,416	1,00	1,218	1,565	0,084	0,302
23	нормальные	0,433	1,25	1,266	1,512	0,067	0,334
24	удлиненные	0,444	1,50	1,284	1,507	0,056	0,341
25	длинные	0,452	1,75	1,301	1,498	0,048	0,349
26	Среднерадиусные: короткие	0,335	0,75	1,167	1,432	0,165	0,332
27	укороченные	0,375	1,00	1,250	1,400	0,125	0,375
28	нормальные	0,403	1,25	1,306	1,383	0,097	0,403
29	удлиненные	0,417	1,50	1,333	1,375	0,083	0,417
30	длинные	0,430	1,75	1,359	1,368	0,070	0,430
№	Название эталона	Icz	Ilz	lei	Icom	las	lipi
31	Мелкорадиусные: короткие	0,285	0,75	1,177	1,309	0,215	0,392

Продолжение табл. 1

№	Название эталона	Icz	Ilz	lei	Icom	las	lipi
32	укороченные	0,342	1,00	1,275	1,310	0,158	0,433
33	нормальные	0,371	1,25	1,334	1,300	0,129	0,463
34	удлиненные	0,389	1,50	1,379	1,288	0,111	0,490
35	длинные	0,408	1,75	1,400	1,296	0,092	0,492
Типичные овоиды
36	Крупнорадиусные: короткие	0,269	0,75	1,169	1,287	0,231	0,401
37	укороченные	0,309	1,00	1,289	1,250	0,191	0,480
38	нормальные	0,342	1,25	1,342	1,255	0,158	0,500
39	удлиненные	0,372	1,50	1,389	1,258	0,128	0,518
40	длинные	0,383	1,75	1,427	1,247	0,117	0,544
41	Среднерадиусные: короткие	0,217	0,75	1,183	1,196	0,283	0,467
42	укороченные	0,276	1,00	1,299	1,203	0,224	0,524
43	нормальные	0,312	1,25	1,374	1,202	0,188	0,562
44	удлиненные	0,340	1,50	1,430	1,201	0,160	0,590
45	длинные	0,356	1,75	1,146	1,534	0,144	0,606
46	Мелкорадиусные: короткие	0,156	0,75	1,191	1,122	0,344	0,535
47	укороченные	0,223	1,00	1,316	1,142	0,277	0,594
48	нормальные	0,264	1,25	1,399	1,149	0,236	0,635
49	удлиненные	0,307	1,50	1,451	1,164	0,193	0,644
50	длинные	0,338	1,75	1,482	1,177	0,162	0,645
Каплевидные овоиды
51	Крупнорадиусные: короткие	0,212	1,00	1,323	1,131	0,288	0,612
52	укороченные	0,254	1,25	1,408	1,138	0,246	0,655
53	нормальные	0,282	1,50	1,474	1,138	0,218	0,693
54	удлиненные	0,305	1,75	1,532	1,137	0,195	0,728
55	длинные	0,332	2,00	1,555	1,147	0,168	0,724
56	Среднерадиусные: короткие	0,169	1,00	1,337	1,094	0,331	0,669
57	укороченные	0,213	1,25	1,426	1,105	0,287	0,713
58	нормальные	0,250	1,50	1,500	1,111	0,250	0,750
59	удлиненные	0,277	1,75	1,553	1,115	0,223	0,777
60	длинные	0,300	2,00	1,600	1,117	0,200	0,800
61	Мелкорадиусные: короткие	0,122	1,00	1,345	1,063	0,378	0,723
62	укороченные	0,175	1,25	1,445	1,079	0,325	0,770
63	нормальные	0,212	1,50	1,516	1,087	0,288	0,804
64	удлиненные	0,249	1,75	1,578	1,095	0,251	0,829
65	длинные	0,259	2,00	1,643	1,089	0,241	0,884

Конусовидные овоиды
№	Название эталона	Icz	llz	lei	Icom	las	lipi
66	Крупнорадиусные: короткие	0,159	1,25	1,449	1,069	0,341	0,790
67	укороченные	0,189	1,50	1,522	1,074	0,311	0,834
68	нормальные	0,222	1,75	1,603	1,078	0,278	0,882
69	удлиненные	0,249	2,00	1,643	1,085	0,251	0,894
70	длинные	0,150	1,50	1,541	1,055	0,350	0,891
71	Среднерадиусные: короткие	0,185	1,75	1,618	1,061	0,315	0,933
72	укороченные	0,213	2,00	1,667	1,067	0,287	0,955
73	нормальные	0,147	1,50	1,541	1,053	0,353	0,895
74	удлиненные	0,180	1,75	1,621	1,059	0,320	0,942
75	длинные	0,209	2,00	1,667	1,065	0,291	0,959
76	Мелкорадиусные: короткие	0,139	1,75	1,649	1,042	0,361	1,011
77	укороченные	0,171	2,00	1,705	1,048	0,329	1,035
78	нормальные	0,157	1,75	1,720	1,043	0,343	1,063
79	удлиненные	0,125	2,00	1,743	1,032	0,375	1,119
80	длинные	0,116	2,00	1,745	1,029	0,384	1,129

Эти эталоны, показавшие свою эффективность к исследованным яйцам, можно использовать для построения эталонов остальных форм. Последние были получены путем совмещения (составления) базовых овоидов инфундибулярными зонами (тупыми полюсами) (рис. 11).

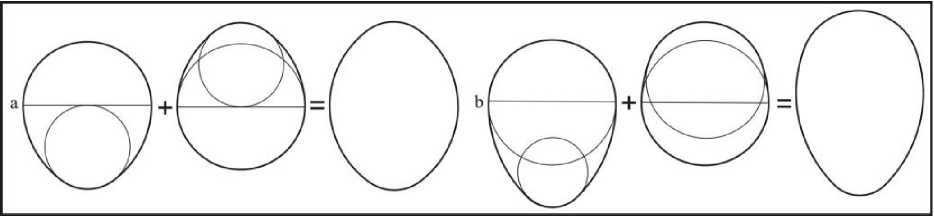
Рис. 11. Схемы составления симметрических (а) и асимметрических (Ь) псевдоовоидов

Получаемые при этом фигуры были названы нами «псевдоовоидами»; их инфундибулярный радиус меньше половины диаметра в отличие от такового у базовых овоидов. При совмещении между собой разных базовых овоидов получаются эталоны асимметрических псевдоовоидов. Комбинации одинаковых овоидов дают совокупность симметрических псевдоовоидов (рис. 12).

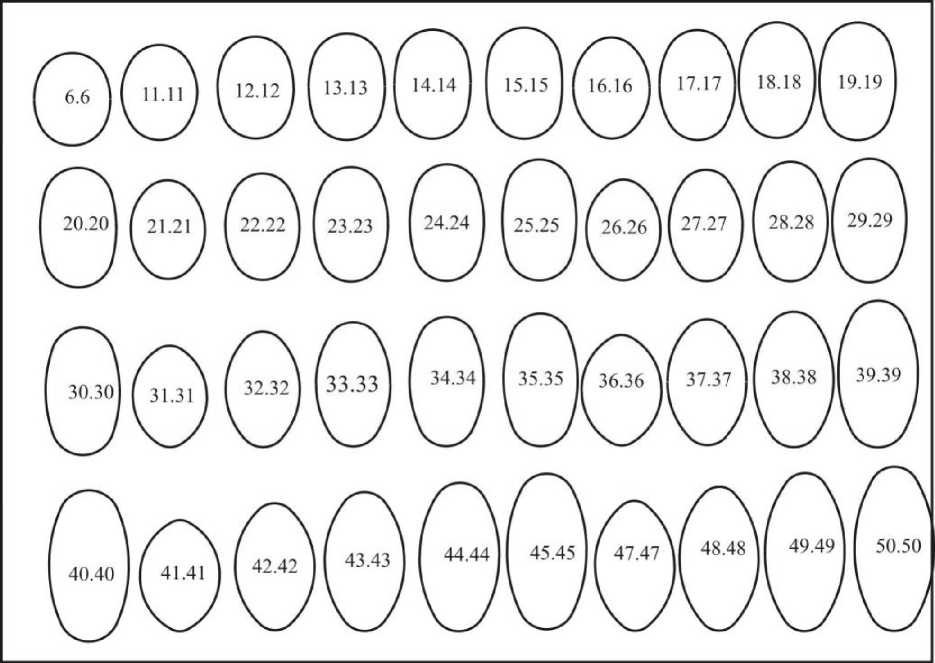
Рис. 1 2. Геометрические эталоны симметрических псевдоовоидов

При этом необходимо также учитывать то, что в природе яйца с абсолютно равными радиусами полярных зон практически отсутствуют. Поэтому к этой категории яиц мы предлагаем относить формы с индексом асимметрии не более 0,05. У птиц симметрические яйца встречаются гораздо реже (в пределах 5%, п=16490), чем у других животных, например, у рептилий. Это связано с множеством причин, среди которых наиболее существенными, на наш взгляд, являются три: а) некомпактность кладки; б) увеличенное раскатывание яиц; в) невозможность фиксированного направления зародышевого диска в сторону обогрева. Симметрические псевдоовоиды в незначительных количествах встречаются у представителей разных отрядов; они отсутствуют у Gaviiformes и Charadriiformes.

Совмещение 80 одинаковых эталонов базовых овоидов дает 80 теоретически возможных симметрических псевдоовоидов. У птиц таких форм меньше. У них отсутствуют крайние, т.е. приближающиеся к сфере и очень длинные и заостренные формы, хотя у других животных такие яйца являются нормой. Анализ нашей базы (п=16490) показал, что реальным формам яиц соответствуют 44 предлагаемых нами эталона.

Названия в данном случае даются, как и для базовых овоидов, с добавлением слов симметрический псевдоовоид. Цифровой код представляет собой двойной порядковый номер базового овоида, например, «тупой крупнорадиусный укороченный симметрический псевдоовоид (22.22)». Максимальное количество яиц относится к

Вестник ТвГУ. Серия "Биология и экология". 2014. № 1 асимметрическим псевдоовоидам (73,4%)- Их геометрические эталоны получаются путем совмещения разных базовых овоидов. Названия при таком подходе получаются очень длинными, т.к. включают в себя названия двух разных базовых овоидов. Поэтому для классификации яиц этого типа мы выбрали более простой способ.

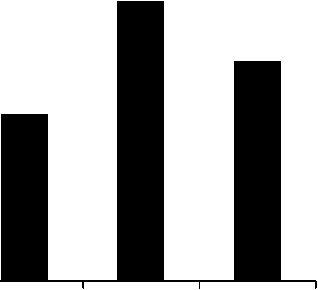
Как отмечалось выше, у асимметрических псевдоовоидов радиусы дуг инфундибулярной зоны меньше 0,5D, но всегда больше, чем радиусы клоакальных дуг. Поэтому, сопрягая инфундибулярные дуги разного радиуса с 80 базовыми овоидами, мы получим совокупность эталонов асимметрических псевдоовоидов. Анализ нашей оологической базы данных показал, что радиусы инфундибулярных дуг рассматриваемого типа яиц колеблются в пределах от 0,285D до 0,491D. Всю эту совокупность мы условно разделили на шесть групп (рис. 13).

4500 -

3000 .....

2500 -

2000 -

1000 -

500 -

0,400     0,418      0,437     0,455     0,473     0,491

Рис. 13. Распределение асимметрических псевдоовоидов по радиусам инфундибулярных дуг

Учитывая то, что формы, входящие в состав каждой из групп, отличаются только радиусами инфундибулярной дуги, их названия складываются из названия базового овоида и номера группы. Шифр состоит из комбинация цифр, отражающих номер базового овоида и номер группы, например: тупой крупнорадиусный укороченный псевдоовоид второй группы (22.2). Количество эталонов в каждой группе разное и уменьшается по мере совпадения радиусов инфундибулярной и клоакальной дуг.

Первая группа включает 75 эталонов, у которых инфундибулярный радиус находится пределах 0,491D>ri>0,474D. По форме эта группа наиболее близка к базовым овоидам (рис. 14). Среди асимметричных псевдоовоидов таких яиц 46,24% (п=12104). Чаще всего они встречаются в отрядах Charadriifomies и Passerifonnes. Их можно встретить также в отрядах Falconiformes, Gallifonnes, Gruifonnes и Piciformes. Индекс удлиненности таких яиц находится в пределах: 1,125<1е1<1,798.

Рис. 14. Асимметрические псевдоовоиды первой группы

Вторая группа (рис. 15) включает 68 эталонов с инфундибулярными радиусами 0,474D>ri>0,456D. Индекс удлиненности этих яиц находится в пределах 1,129<1е1< 1,803.

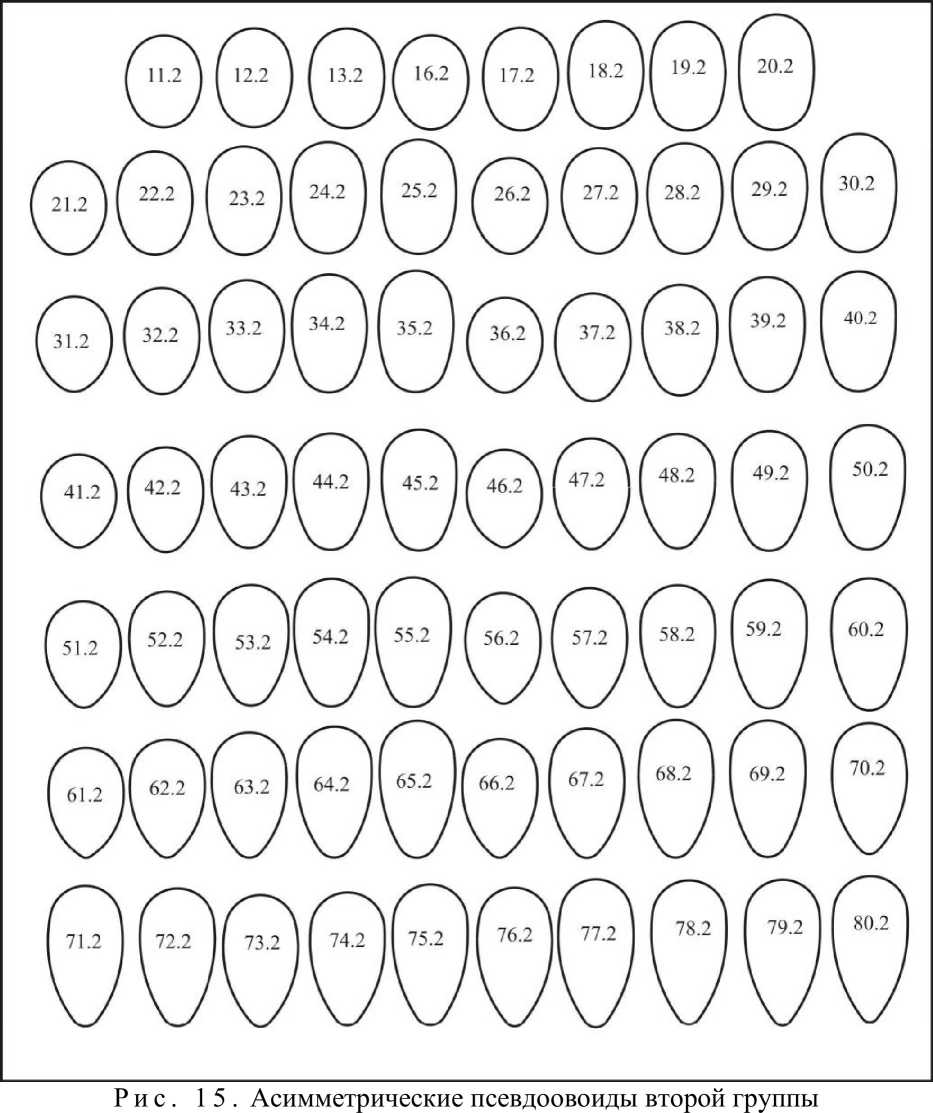
Среди асимметрических псевдоовоидов таких яиц 28,43%. Их больше всего в указанных выше отрядах. Появляются они у Anseriformes, Ciconiiformes, Strigiformes, Apodiformes, Cuculiformes, Coraciiformes и Upupiformes.

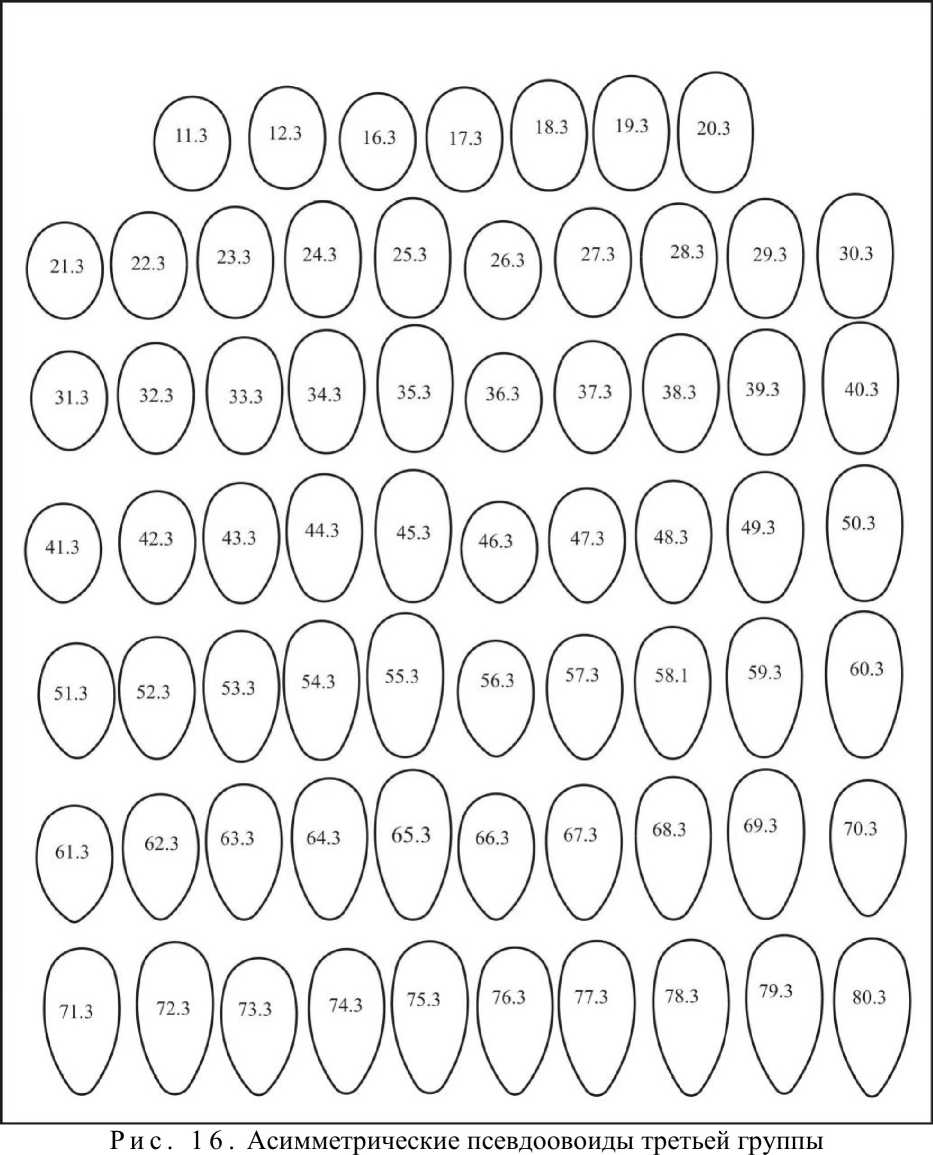
В третью группу (рис. 16) входят 67 эталонов, инфундибулярные радиусы которых находятся в пределах 0,456D>ri>0,437D. Индекс удлиненности этих яиц - 1,134<1е1<1,786.

Четвертая группа (рис. 17) представлена 60 эталонами, у которых инфундибулярный радиус находится в пределах 0,437D>ri>0,419D. Индекс удлиненности 1,150<1е1<1,806.

Указанные формы встречаются в 12,34% случаев. Максимальное их количество отмечается в отрядах Anseriformes, Falconiformes, Galliformes, Gruiformes, Strigiformes, Upupiformes, Piciformes и Passeriformes. Они встречаются также у Gaviiformes, Podicipediformes, Ciconiiformes, Coraciiformes, Columbiformes, Pelecaniformes, Procellariiformes, Caprimulgiformes, Cuculiformes, Apodiformes; их число уменьшается у Charadriiformes.

Рис. 17. Асимметрические псевдоовоиды четвертой группы

Таких форм насчитывается 7,54%. По отрядам наблюдается примерно такое же распределение, что и третьей группе.

В пятой группе насчитывается 55 эталонов с инфундибулярным радиусом в пределах 0,419D>ri>0,401D (рис. 18). Индекс удлиненности этих яиц находится в пределах 1,153<1е1<1,672. Таких форм насчитывается 3,44%. Максимальное их количество наблюдается в отрядах Anseriformes, Ciconiiformes Pelecaniformes, Podicipediformes и Gruiformes. В других отрядах (Struthionifomies, Falconiformes, Galliformes, Columbifonnes Strigiformes, Upupiformes, Picifonnes, Passeriformes) их количество сходно небольшое (рис. 18).

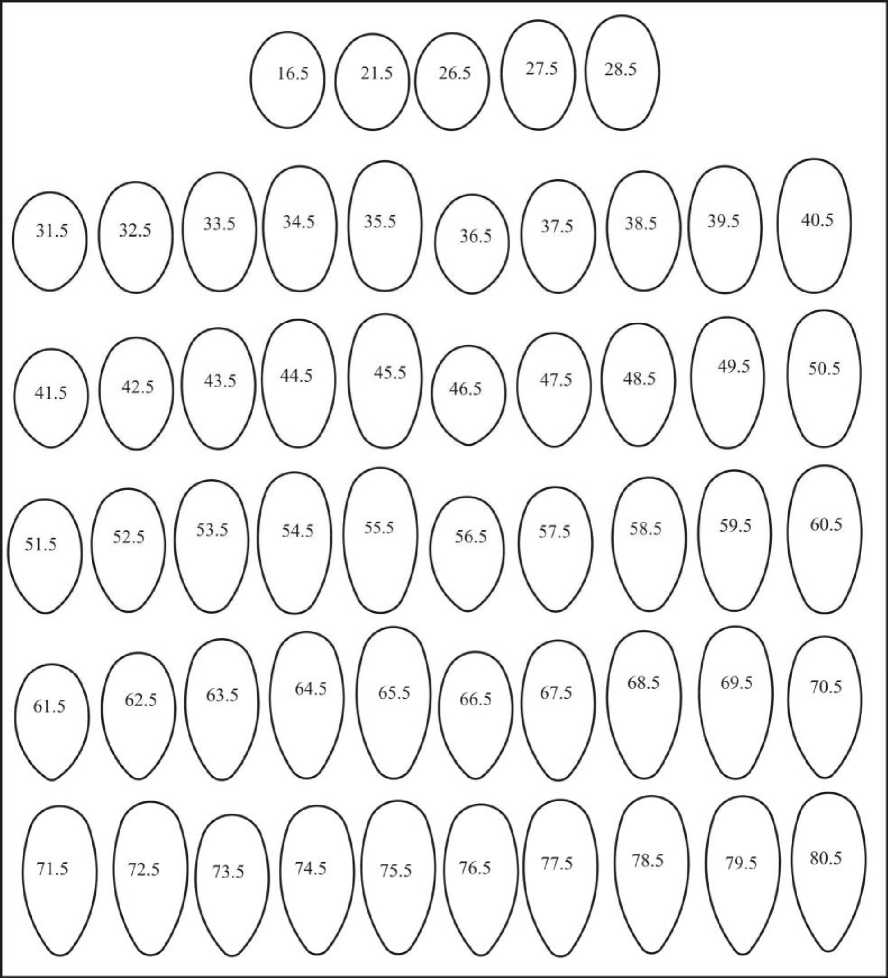
Рис. 18. Асимметрические псевдоовоиды пятой группы

Шестая группа (рис. 19) представлена 50 эталонами с инфундибулярным радиусом 0,409D>ri>0,285D. Индекс удлиненности 1,161<1е1< 2,0. Доля этих форм составляет 2,0%.

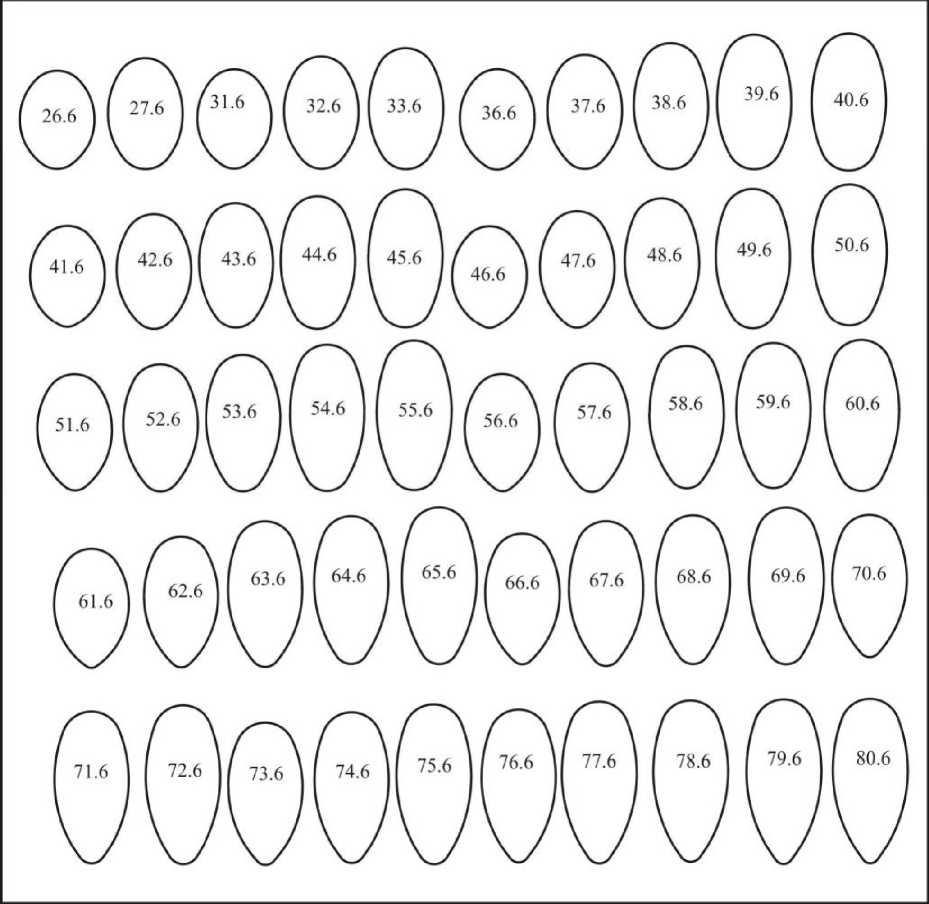
Рис. 19. Асимметрические псевдоовоиды шестой группы

Группа представлена, главным образом, в отрядах Anseriformes, Ciconnformes, Podicipediformes и Pelecaniformes. Такие отряды, как Gaviifonnes, Falconiformes, Caprimulgiformes, Gruiformes и Passeriformes представлены одинаково незначительно; остальные (Caprimulgiformes, Charadriiformes, Galliformes, Upupiformes, Strigifonnes, Piciformes) -единичными экземплярами.

Приведенное выше количество эталонов (п=375) выведено только по средним значениям инфундибулярного радиуса шести групп асимметрических псевдоовоидов. Если по той же схеме вовлечь минимумы и максимумы, то мы получим еще 750 эталонов.

Заключение. Предлагаемая система эталонов форм птичьих яиц дает несколько важных перспектив в оологических исследованиях. Присвоение фиксированного названия и количественного выражения формам яиц путем сопоставления их фотографий с геометрическими эталонами позволяет осуществлять привязку важной биологической информации к любому птичьему яйцу. Простота методики дает

Вестник ТвГУ. Серия "Биология и экология". 2014. № 1 возможность широкого ее применения на различных уровнях: визуальном и компьютерном. В последнем случае возможно использование как существующие, так и специально написанные программы. Унификация и скоординированность оологических работ орнитологов открывает большие перспективы для широкомасштабных обобщений и создания глобальных баз данных.

Митяй И.С. Описание форм птичьих яиц с помощью геометрических эталонов / И.С.

Митяй // Вести. ТвГУ. Сер. Биология и экология. 2014. № 1. С. 125-147.