Описание переходных поверхностей зубьев косозубых колес векторными функциями

Задачи геометрии зубчатых колес и моделирования процесса формообразования зубьев при зубофрезеровании в объемном представлении требуют рассмотрения боковой поверхности зуба. Боковая поверхность зубьев зубчатых колес, как известно, состоит из двух частей: эвольвентной LA и переходной М 1 L (рис. 1). Сопряжение профилей происходит в точке L . В статье рассматривается переходная часть боковой поверхности зуба на основе ее описания векторными параметрическими функциями. Отметим, что анализируется частный случай, когда переходная поверхность зуба имеет в торцевом сечении профиль в виде дуги окружности. Такая переходная поверхность формируется при нарезании зубчатых колес с положительным смещением исходного контура зуборезного инструмента [1]. Переходная кривая M 1 L в виде дуги окружности в торцевом сечении зубчатого колеса в локальной системе координат X 1 O 1 Y 1 Z 1 описывается векторной функцией следующего вида:

г ок

Р а 0 sin Y

Р а 0 cos Y

где γ – угол поворота радиус-вектора r ок , модуль которого равен значению радиуса ρ a0 .

В системе координат XOYZ вектор переходной кривой, восстановленный в точку M, определяется выражением r п.п.к

Ра 0 sin Y f + Ра0 cos Y

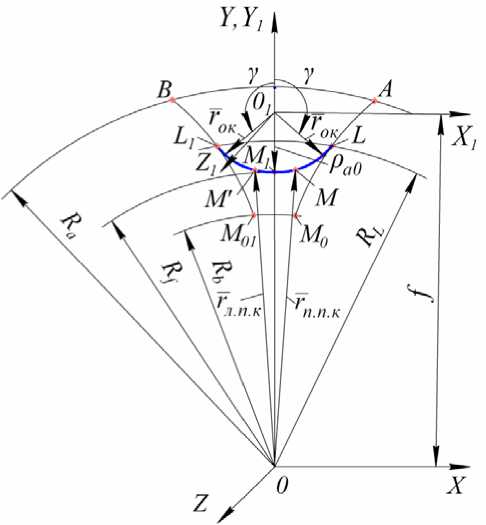
Рис. 1. Образование переходной кривой:

R b – радиус основной окружности; R f – радиус окружности впадин; R L – радиус окружности сопряжения частей профиля; R_a – радиус окружности вершин; ρ _a0 – радиус скругления переходной кривой; О₁ – центр скругления; f – координата центра скругления О 1 в системе координат XOYZ ; М 0 А и М 01 В – эвольвенты.

Формула (2) описывает переходную кривую М 1 L , соответствующую профилю зуба только с одной стороны. Второй переходный профиль М 1 L 1 образуется таким же образом, как и профиль М 1 L , только в данном случае угол γ имеет отрицательное значение. С учетом этого векторная функция левой, относительно оси OY , переходной кривой запишется:

r л..п.к

- Р а 0 sin Y ^f + Р а 0 cos Y 0

Положение произвольной точки М правой винтовой переходной поверхности М1М1'L'L (рис. 2) косого зуба определяется векторной функцией г......

ï . ï .. ï

f sin Ф 1 + p . O sin ( Y + Ф 1 ) f cos Ф 1 + p . о c^{os (} Y + Ф 1 )

- а ф 1

где φ 1 – угол поворота проекции вектора r п . п . п на плоскость XOY ; а – параметр, характеризующий движение по винтовой линии вдоль оси колеса OZ . Текущий параметрический угол φ 1 изменяется в пределах от своего нулевого значения, до значения φ 1max , которое он принимает на тыльном торцевом сечении зубчатого колеса. Величина φ 1max определяется по формуле

b

Ф 1тах = — tg P b R_b

,

где βb – угол наклона линии зуба на основном цилиндре; b – ширина зубчатого венца колеса. Соответственно положение произвольной точки М' левой переходной поверхности М1М1'L1L1 описывается векторной функцией f sin Ф1 - Ра о sin (Y - Ф1 )

Г л.п.п

f cos Ф 1 + Р а о co^{s (} Y ^- Ф 1 )

- ^{а Ф} 1          J (6)

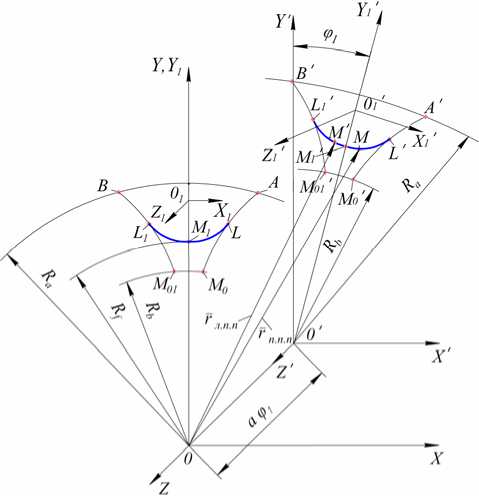
Рис. 2. Переходные поверхности

Формулы (4) и (6) описывают переходные поверхности, у которых во фронтальном торцевом сечении зубчатого колеса начальная точка М 1 профиля расположена на оси OY системы координат. При образовании формы зуба колеса боковые поверхности располагаются таким образом, что они охватывают его тело симметрично оси OY . С этой целью векторные функции (4) и (6) поворачиваются на угол ψ 2 (рис. 3). Причем векторная функция (4), описывающая правую переходную поверхность, поворачивается против часовой стрелки, а функция (6) – по часовой стрелке. Угол поворота ψ 2 определяется из схемы фронтального торцевого сечения зубчатого колеса, показанного на рис. 3. При его нахождении учитывается, что толщина зуба S t =M'M'' по делительной окружности радиуса R имеет заданное значение. При повороте профиля зуба из положения М 1 LMA в положение М 11 L 11 М''А 1 угол ψ 2 равняется сумме углов

¥ 2 = V + ¥1

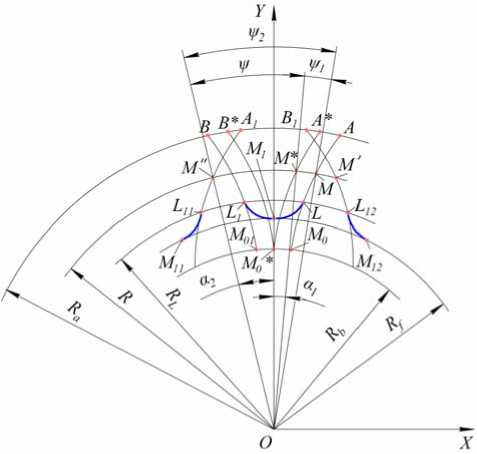
Рис. 3. Фронтальное торцевое сечение

В формуле (7) угол ψ находится как сумма углов

¥ = a 1 + a ₂

где α1 – эвольвентный угол эвольвенты М0*А* в точке М*. Значение угла α2 вычисляется по формуле a 2

P t = m_n n 4 R 4 R cos в

где P _t - окружной шаг зубьев; m _n - нормальный модуль зубьев; β – угол наклона зубьев по делительному цилиндру. Угол ψ 1 определяется из схемы формирования переходной кривой (рис. 4). Значение угла ψ 1 равняется разнице углов

Векторная функция ^г л . п . п . з левой боковой переходной поверхности зуба косозубого ко-леса M ii M ii' Ln'Ln (рис. 5) запишется:

г...... = 1/1 г......

е . i . i . q                           i . i . i

V 1 = ^a w ^- V _l

где [M] – матрица поворота на угол ψ 2 против часовой стрелки:

где α w – угол зацепления; φ L* – угол развернутости эвольвенты М ₀ А в точке L . Угол ф_L * определяется зависимостью [2]:

V l

^^^^™

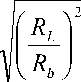
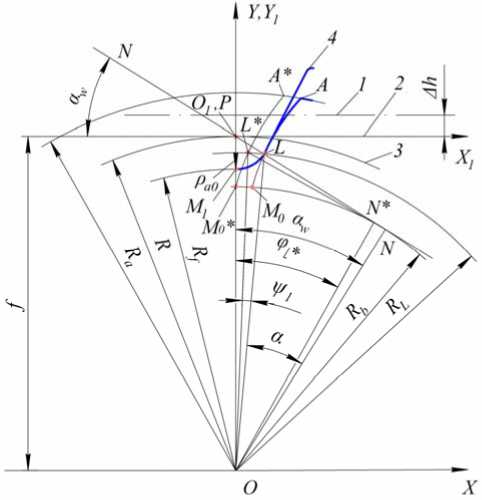
Рис. 4. Формирование переходной кривой:

1 – средняя линия исходного контура рейки 4; 2 – начальная прямая; 3 – начальная (делительная) окружность; NN - линия зацепления; Р - полюс зацепления; ^h - смещение исходного контура

Радиус R _l цилиндра сопряжения переходной и эвольвентной поверхностей зуба колеса вычисляется по формуле

R

L

cos а

	COS V 2	- sin v 2	0 "
[ M ] =	sin V 2	COS V 2	0
	_      0	0	1 .	.     (15)

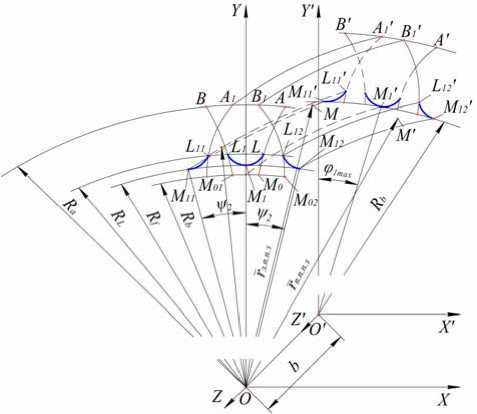
Рис. 5. Переходные поверхности зуба

После перемножения матрицы [M] и функции ^Г п . п . п векторная функция r , . п . п . з принимает вид:

r л.п.п.з

^f Sin ( ф 1 - V 2 ⁾⁺ Р а 0 Sin ⁽ r ⁺ Ф 1 -Ф 2 ) f cos ⁽ V 1 ^-V 2 ⁾⁺ Р а 0 ^{cos (}Y ⁺ Ф 1 ^- Ф 2 )

^{- а} Ф 1

Соответственно векторная функция правой боковой переходной поверхности зуба косозубого колеса M ₁₂ M ₁2' L ₁₂' L ₁2 запишется:

r.Hq = [ ^ 1 ] ^Г»Л

где а - угол профиля эвольвенты М ₀ Л в точке сопряжения L :

LN а = arctg

R^b .               (13)

Длина отрезка LN имеет значение LN = R _b tga _w - p aO .

где [M 1 ] – матрица поворота на угол ψ 2 по часовой стрелке:

[ M , ] =

cos v 2	sin v 2	0 "
- sin v 2	cos v 2	0
0	0	1 .

После преобразований векторная функ- ция rп.п.п.з принимает вид:

п . п . п . з

f sin (ф, + V 2 )- Ра о sin (J - фх - V2 ) f cos(^i + V 2 )+ Ра о cos(Y - Ф1 - V 2 )

- ^а ф 1

Формулы (16) и (19) описывают боковые винтовые переходные поверхности первого зуба колеса. Переходные поверхности второго и последующих зубьев колеса описываются векторными функциями, которые получаются путем умножения функций (16) и (19) на матрицу

[ M . ] =

cos V 3 sin v 3 0

- sinV3 cosV3 о

0  01

( i - 1 ) 2 n где ^V з =--------- .

z

В формуле (20) номер зуба i принимает значение от 1 до числа зубьев z.

Выводы: определены зависимости для описания боковых винтовых переходных поверхностей зубьев цилиндрического косозубого колеса, выраженные параметрическими векторными функциями, использование которых необходимо при моделировании формообразования в процессе зубообработки.