Описание срединной поверхности стенки круговой арки с непрерывными поперечными треугольными гофрами

Состояние вопроса . Попытки применения арок из сварного двутавра с тонкой волнистой стенкой (без описания ее геометрии и напряженног состояния) в качестве несущих конструкций покрытий сельскохозяйственных зданий приведены в [1, 2, 3 и др.]. Первое описание геометрии гофрированной стенки арки было предложено в 1999 г. [4], но при этом для упрощения треугольный, трапецеидальный и другие профили представлены синусоидальным, что приводит к некоторому искажению напряженного состояния поперечных сечений даже в прямолинейных стержнях.

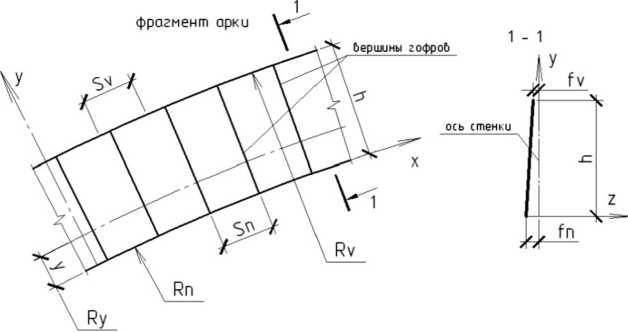
Рис. 1. Фрагмент стенки арки и ее сечение по вершине гофра

Из известных и используемых в гофрированных балках и арках профилей гофров в их стенках наиболее рациональным по картине напряженного состояния поперечных сечений и наиболее простым в изготовлении является треугольный гофр [5, 6]. Он непрерывно описывается по длине изогнутой по дуге окружности оси арки, а сама арка с гофрированной стенкой представляется тонкостенным стержнем с периодически изменяемой геометрией поперечного сечения.

Геометрия гофров. Для непрерывного описания срединной поверхности стенки круговой арки, изогнутой в плоскости стенки с радиусом кривизны нижнего пояса Rn (его ось принимается за ось арки), выполненной из двутавра высотой сечения h с непрерывным треугольным профилем поперечных гофров в стенке (рис. 1), можно воспользоваться периодической функцией в виде ряда

2 ( x , y ) = f ( y ) • -8 2 • z ( - 1) ^k • ⁿ k = 0

sin ( 2 • k + 1 ) - ^ x

L ⁽          ) s ( У ) J ,

( 2 • k + 1 ) ²

где f ( y ) – максимальное отклонение вершин гофров от оси стенки на высоте y от ее низа. По высоте стенки оно переменное, причем с удалением от нижнего пояса арки оно уменьшается.

При формовании стенки из прямоугольной полосы без учета возможных незначительных удлинений ее в продольном направлении можно допустить, что длина волокон полуволны гофра по высоте стенки остается постоянной, т.е.

V(2 f n )² + S n²    ^( = f v )² + S v²      (2= f y )² + S y ² ,

Принятые параметры

Rn     радиус кривизны нижнего пояса арки (см)

h      высота гофрированной стенки (см)

fh      высота полуволны гофра у нижнего пояса (см)

L      пролет нижнего пояса

(см)                 ж                     /                             х m число полуволн гофров в стенке арки (задается четным числом)

Дополнительные параметры определяющие график поверхности

SL :- a Rn

_ . ( L а := 2 asm -----

длина арки у нижнего пояса (см)

центральный угол охвата арки (рад)

длина полуволны гофра у нижнего пояса арки (см)

высота полуволны гофра у верхнего пояса (см)

Фб = -m

центральный угол охвата 1-ой полуволны

x(R,i|>) := R ■ соз(-ф)

y(R ,ф) := R ■ sin(ip)

функции описание поверхности стенки

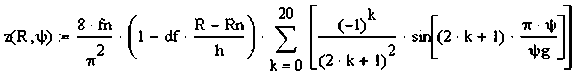
Rlow := Rn           Rhigh := Rn + h „ ,   ,

Rnl := 5

границы переменных и сетка их разбивки

(it                  fa  it A

V 2   2 J             V 2   2 ) Фп := 300

оператор поверхности

Рис. 2. Алгоритм построения графика поверхности стенки по средствам программного комплекса Mathcad откуда при 0 <  y <  h получим величину высоты

2 n____ I fn J и длины полуволны гофра на уровне у высоты стенки

^s( y) = s n • I ^{1 +} 1^1 .

V R n )

f ( y ) = fn • 1

s

2 •

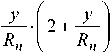
Изменение высоты гофра f(y) по высоте стенки h приближается к линейному при h / R n ≤0,03 и S n / f n ≤10 , поэтому при соблюдении последних отношений формование гофров в стенке не должно вызвать ее повреждений и позволяет принять в расчетах:

f ( y ) = f_n - f-^f • y •

h

Для исключения выпрямления стенки у верхнего пояса и возможного при этом уменьшения высоты гофров у нижнего пояса высота последних должна быть не менее

•

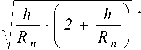
min fn sn

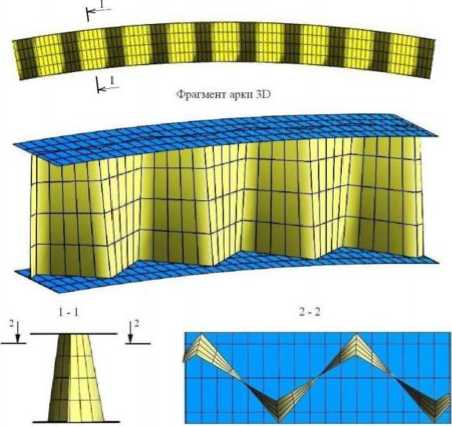
Рис. 3. График поверхности профилированной стенки гофрированной арки, а также верхнего и нижнего поясов (для наглядности)

Определить параметры гофров и точек произвольного сечения стенки арки удобно с использованием средств программного комплекса Mathcad, например путем построения графика поверхности, алгоритм которого представлен на рисунке 2.

График поверхности профилированной стенки гофрированной арки, а также верхнего и нижнего поясов, построенного посредством программного комплекса Mathcad, представлен на рисунке 3 (3D вид спереди, разрез 1-1, разрез 2-2), где отчетливо видно периодическое изменение геометрии поперечного сечения арки.

Заключение. Представленная периодическая функция (1) позволяет непрерывно описать профилированную стенку гофрированной арки и определить необходимые для расчетов геометрические и секторальные характеристики произвольного поперечного сечения арки.