Описание течения жидкости с учетом дефектов структуры
Автор: Михайлов Е.В., Наймарк О.Б.
Статья в выпуске: 7, 1999 года.
Бесплатный доступ
Разработан подход к описанию течения жидкости, учитывающий наличие в ее структуре дефектов. На основе статистической модели среды c дефектами (микросдвигами) получена система уравнений, описывающая течение жидкости с учетом кинетики накопления микродефектов. Проведены численные исследования, показывающие, что модель описывает режимы течения жидкости, наблюдаемые при экспериментальных исследованиях турбулентных пятен.
Короткий адрес: https://sciup.org/146211216
IDR: 146211216 | УДК: 532.529
Текст научной статьи Описание течения жидкости с учетом дефектов структуры
Известно, что жидкости по своей структуре занимают промежуточное положение между твердыми телами и газами. При этом, обычно, для расчета течений жидкостей используются уравнения, отражающие более явную аналогию в поведении газов и жидкостей. Однако еще Я. Френкель указывал на близость механизмов течения жидкостей и твердых тел как конденсированных сред, отмечая, что “... рентгенограммы жидкостей сходны с рентгенограммами микрокристаллических тел и их можно было бы интерпретировать в общих чертах, исходя из представления, что жидкость состоит из большого числа беспорядочно ориентированных кристалликов субмикроскопических размеров” и “... широко распространенное представление о том, что текучесть жидкостей обусловлена отсутствием упругости на сдвиг, т.е. равенством нулю модуля сдвига ... ошибочно (за исключением, может быть гелия II)” [1].
Подтверждением справедливости последнего утверждения являются данные по измерению комплексного модуля сдвига некоторых жидкостей [2], которые указывают на существование в спектре исследованных жидкостей характерных времен релаксации τ ~10 - 5c, отличающихся на семь порядков от дебаевских времен. Данный факт говорит о существовании в структуре жидкости элементов, для релаксации которых требуется значительно большее время, чем для процессов, определяющих диффузию импульса.
Другим подтверждением определенного структурного подобия жидкостей и твердых тел являются эксперименты по определению эффективной вязкости конденсированных сред (сталь, алюминий, свинец, медь, оргстекло, ртуть, вода) при ударном нагружении [3,4]. Как твердые тела, так и жидкости при скорости деформации ε & ~ 105c - 1 обнаруживали близкие значения эффективной вязкости η ~103 Па ⋅ с , что можно объяснить наличием схожих механизмов диссипации энергии в твердых телах и жидкостях, которые начинают играть доминирующую роль при больших скоростях деформации. В качестве такого механизма диссипации в работе [4] предполагается образование дефектов за фронтом ударной волны.
Однако остаются открытыми вопросы как о выборе и построении модели поведения жидкостей с “дефектной структурой”, так и о модельных экспериментах, которые могли бы использоваться для подтверждения высказанной гипотезы.
В [5] было сделано предположение о возможности смены механизма переноса импульса от диффузионного, описываемого ньютоновским законом связи напряжения и скорости деформации, к механизму, типичному для пластического течения твердых тел, связанному с появлением специфических носителей - дислокаций. Отметим, что появление этого механизма в интенсивных силовых полях вызвано, в соответствии с моделью Френкеля-Конторовой, образованием связанных молекулярных конфигураций, перемещающихся как единое целое с некоторой групповой скоростью.
Физически, введение этого механизма в рассмотрение означает, что при воздействии на конденсированную среду (в данном случае - жидкость) не исключается сценарий, когда механизм переноса импульса, обусловленный движением связанной конфигурации молекул (молекулярного роя, по терминологии Френкеля [1]), может рассматриваться как конкурентоспособный с обычным молекулярным механизмом.
Возможность образования качественно новых носителей деформации обусловлена, естественно, появлением дополнительных переменных состояния, геометрические, кинетические и термодинамические свойства которых могут быть определены с учетом реальных механизмов зарождения дефектов и их динамики.
Учитывая тот факт, что дислокации отражают деформационную несовместность, обусловленную неустойчивостью деформации, параметры, определяющие вклад в кинетику новых носителей могут быть введены как на основе континуальной теории дислокаций, так и на использовании теории калибровочных полей, где кинематические переменные, характеризующие дефекты, определены на основе локализации так называемой группы симметрии компонент тензора дисторсии, ответственных за “несовместности” трансляционного (дислокационного) и ротационного (дисклинации) типов [6].
Следуя [5], ограничимся рассмотрением дефектов трансляционного типа, каждый из которых представим в виде “микроскопического” сдвига интенсивности s в направлении l на некоторой площадке с нормалью V :
s ik = 2 s ( V iik + i k v i ) . (1)
В качестве кинетического уравнения, описывающего эволюцию во времени параметра s ik , используются уравнения Ланжевена для случайной величины:
S ik = K ik ( S im ) - F ik , (2)
где K ik ( s lm ) и F ik соответственно детерминированная и случайная части силового поля, удовлетворяющие условиям ( F ik . ( t )} = 0, ( Fik ( t ') Fik ( t )} = Q 5 ( t - t '), где Q - коррелятор флуктуирующих сил (неравновесный потенциал, определяющий энергетический потенциал системы). Функция распределения дефектов по размерам и ориентациям W ( s, V , l ) в фазовом пространстве состояний дается уравнением Фоккера-Планка:
5 д \1 5^5)
W = -^ ( Kik(sim ) w ) + /2,- I ^W | . (3)
5 1 5 s ik x x ’ ' 2 5 s ik <5 s ik 7
Решение уравнения Фоккера-Планка (3), основанное на предположении о статистической автомодельности в распределении дефектов, позволяет представить функцию распределения W ( s , V , l ) в виде
W = Z 1 exp ( EQ ) , (4)
где Z рассматривается как обобщение статистического интеграла.
Энергию микродефекта в приближении самосогласованного поля с точностью до постоянного слагаемого можно записать в виде
E = E 0 - Hiksik + a sik , где Eо =- ;1 X (sik )2, Hik
- эффективное силовое поле, a и X — константы материала.
Эффективное поле Hik предполагается пропорциональным макронапряжению стik и макроскопическому тензору плотности дефектов, определяемому усреднением тензора sik по элементарному объему pik = nsik :
Hik = γσ ik + λ pik , (6)
где n — концентрация микродефектов. Второе слагаемое в (6) определяет силовое воздействие на микродефект, создаваемое полями окружающих ее дефектов.
Осредняя sik с функцией распределения (4), можно получить макроскопическую деформацию, обусловленную дефектами, pk = n J sikW(s, V, Г) dsd3 v d3 Г. (7)
Решение уравнения (7) для случая простого сдвига бесконечного слоя представлено на рис. 1 в виде зависимостей p = pxz от σ = σ xz для различных значений параметра δ= 2 αλ n. Переходы к эквивалентным классам кривых реализуются при достижении параметром δ критических значений δ 1 и δ 2 , являющихся точками бифуркаций.
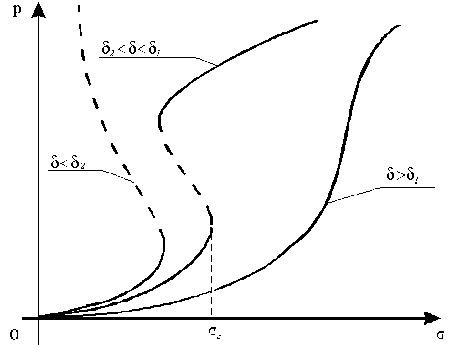
Рис. 1. Реакции среды с микродефектами при различных значениях δ
Более полный анализ зависимости σ ( p ) для различных δ можно осуществить, вычисляя потенциал - аналог свободной энергии среды, обусловленный микродефектами F ∗ =- nQ ln Z . Как показано в [7], условие равновесия ∂ F ∗ ∂ p = 0
совпадает с (7), что дает возможность, в частности, выбрать термодинамически устойчивые реакции среды. Равновесные значения параметра p , соответствующие минимуму потенциала, показаны на рис. 1 сплошной линией, неустойчивые - пунктирной.
Из условия знакоопределенности диссипативной функции, которая по сути является выражением второго закона термодинамики
TP s
qk ∂ T ν - δ F ∂ pik +σ ik e ik -
T ∂ x k δ pik ∂ t
≥ 0,
можно получить определяющие уравнения среды
^ ik = 2 n e v k + X P ik ,
δ F δ pik
ν
=- χ ei ν k + ς pik ,
где n , Z и X — кинетические коэффициенты, имеющие размерность вязкости, о k - девиатор напряжений, е^ - “вязкая” составляющая полной скорости деформации e ik = e ik + p ik .
Поведение моделируемой “среды с дефектами” удобно исследовать, обращаясь к кривым, представленным на рис. 1. В зависимости от значения параметра 5 можно представить три различных типа поведения. Область 5 > 5 1 соответствуют флуктуациям поля смещений и скоростей деформаций, обусловленных дефектами, которые имеют вид слабых периодических пульсаций скорости, не меняющих характер ламинарного течения. Переход через точку бифуркации 5 1 (область 5 2 < 5 < 5 1) приводит к зарождению в потоке волн типа автосолитонов, порождаемых в результате ориентационной неустойчивости в ансамбле микроскопических сдвигов. В области 5 < 5 2 формируются условия для возникновения пространственно-локализованных диссипативных структур с взрывной кинетикой роста интенсивности микросдвигов.
Сопоставим качественный сценарий развития неустойчивости, определяемый динамикой p ik , с реально наблюдаемым развитием возмущений в турбулентном потоке. Экспериментальные данные по визуализации турбулентного потока в плоском течении Пуазейля [8] показали, что области неустойчивости в виде турбулентных пятен наблюдаются при Re = 840-1500 и имеют форму треугольного крыла с углом раскрытия 15-20 ° (рис.2). Турбулентное вихревое движение возникает внутри пятен, на границе которых генерируются конечноамплитудные возмущения в виде “наклонных” волн (oblique waves [8]), затухающих при движении в ламинарную зону. При движении указанных волн в направлении пятна наблюдается вторичная неустойчивость, приводящая к росту возмущений и увеличению размеров пятна.

Рис. 2. Визуализация турбулентного пятна в плоском течении Пуазейля: Re = 10 3
Этот экспериментально наблюдаемый сценарий качественно согласуется с предсказанием представленной модели, где развитие возмущений связывается с эволюцией микродефектов.
Статистическое описание ансамбля микродефектов позволило предложить макроскопическую модель, основанную на феноменологическом представлении свободной энергии в виде разложения Ландау по тензору плотности микродефектов pik и на зависимости коэффициентов разложения от параметра 5, что обеспечило смену ассимптотик при увеличении интенсивности течения:
F * = D
1 A о 5 Р 2 - ^ BP 4 + 6 C о ( 5-5 2 ) Р 6 - Р о
где A o , B, C o , D — константы аппроксимации, причем B =
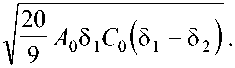
Учет эффектов, обусловленных пространственной неоднородностью распределения p ik , обеспечивается введением квадратичного по градиенту p ik члена в выражение свободной энергии (разложение Гинзбурга-Ландау) [9]:
F = D
2 A 0 6 p 2 - 4 Bp 4 + 6 C 0 ( 8-8 2 ) p6
- p О
- 1 MV p ) 2.
Используя определяющие соотношения (9), потенциал свободной энергии (11) и уравнения движения, получаем систему уравнений, описывающую несжимаемой жидкости с учетом кинетики накопления микросдвигов:
( 8v ,_ . ।pHr + (v "V)v l=V-o,V дt )


