Описание технической архитектуры системы управления предприятием связи с использованием тензорной методологии анализа систем

Работу современного крупного предприятия всегда сопровождает набор необходимых для осуществления бизнес-деятельности информационных систем: система управления предприятием, система биллинга (для предприятий связи), система электронного документооборота и т. д.

Современные информационные системы в своей работе опираются не только на безупречно спроектированную техническую архитектуру или правильно выбранную систему баз данных, а зачастую обеспечивают стабильную работу за счет сочетания многих параметров. Принято говорить об «интегральном» подходе к обеспечению необходимых характеристик быстродействия и надежности систем.

С 2009 г. на предприятии связи макрорегиональ-ного филиала «Сибирь» ОАО «Ростелеком» эксплуатируется система управления предприятием на базе Oracle E-Business Suite.

В данной работе рассмотрен подход к оценке и повышению быстродействия системы управления предприятием. Для описания технической архитектуры системы управления предприятием предлагается ис- пользовать тензорную методологию, которая позволяет представить систему в виде удобного для дальнейшего анализа набора величин.

При проектировании системы управления предприятием параметры производительности системы были рассчитаны исходя из определенного объема данных и количества работающих пользователей. В ходе эксплуатации эти параметры были превышены. Кроме того, исходя из изменения законодательства и требований бизнеса, был изменен код системы, что также ухудшило быстродействие.

В результате в определенный момент времени пользователи начали ощущать заметное замедление работы системы управления предприятием. Данное замедление является критичным для деятельности компании, поскольку не позволяет своевременно выполнить бизнес-процессы и получить необходимую отчетность.

Специалистами ИТ-блока компании был проведен анализ ситуации и намечен план решения проблемы, в который вошли следующие мероприятия.

• 1.    Оптимизация производительности работы расширений.

• 2.    Разработка и внедрение процедур планирования запуска задач.

• 3.    Модернизация вычислительного комплекса.

В рамках данных работ были выявлены программы, которые выполнялись наиболее долго либо создавали наибольшую нагрузку на систему. Была произведена доработка расширений и на промышленный экземпляр установлены оптимизированные версии.

Для обеспечения повышения производительности системы была реализована схема установки приоритетов выполнения пользовательских запросов. В условиях пиковой загрузки системы данный подход дал возможность пользователям обеспечить бесперебойное выполнение важных и срочных бизнес-процессов. Также были подготовлены технические решения, позволяющие регламентировать работу пользователей.

Производительность любой информационной системы, обрабатывающей данные, имеет нелинейную зависимость от количества данных (т. е. при увеличении объема данных в два раза время их обработки увеличивается более чем в два раза). Поэтому параллельно с работами по снижению ресурсоемкости были проведены работы по увеличению мощности вычислительного комплекса: увеличение количества процессоров, увеличение объема оперативной памяти серверов, перераспределение мощности.

Для поиска оптимального решения задачи модернизации вычислительного комплекса была применена тензорная методология анализа систем.

Понятие тензорной методологии анализа систем. Процесс описания разнородных систем с помощью универсальных понятий элемента и структуры приводит к следующему обобщению: множество систем является множеством различных проявлений некоторой обобщенной абстрактной системы, а следовательно, элементы и структуры рассматриваемых систем определенным образом взаимосвязаны. В таком случае, имея результаты анализа одной системы, можно прикладывать их к другим системам с помощью некоторого количества стандартных преобразований. Абстрактная сложная система может быть рассмотрена как геометрический объект, помещенный в некоторое многомерное пространство, а все многообразие существующих систем - как проекции данного объекта в частные системы координат.

Теория преобразований систем координат рассматривается в рамках векторного исчисления. Математическим аппаратом, позволяющим оперировать обобщенными n -мерными пространствами и объектами в них, является тензорный анализ.

Автор тензорной методологии анализа систем -американский ученый и инженер Г. Крон [1; 2]. Крон сделал вывод, что инвариантом преобразований структуры является линейная форма, связанная с каждым элементом сети.

В приложении к теории связи дальнейшее развитие тензорная методология Г. Крона получила в работах [3; 4], в которых впервые использована тензорная методология для анализа вероятностно-временных характеристик в сетях связи.

Узловой метод анализа сети. В узловых сетях воздействующей величиной является интенсивность потока входящих в сеть сообщений X , а величиной отклика - значение длины очереди, возникающей в системе массового обслуживания под действием X при заданных интенсивностях обслуживания.

На первом этапе анализа узловых сетей тензорным методом необходимо установить вспомогательную сеть. К вспомогательной сети предъявляется следующее требование: получение уравнения состояния и компонент участвующих в нем геометрических объектов не должно представлять особой сложности. Простейшим частным случаем вспомогательной сети является примитивная сеть. Примитивная узловая сеть из n ветвей состоит из n не замкнутых обособленных ветвей.

Примитивная узловая сеть содержит n независимых подсетей и 2 n узлов, и, следовательно, имеет 2 n - n = n узловых пар. Два конца каждой ветви образуют узловую пару, через которую поступает и уходит поток сообщений интенсивностью X . Ветвь представляет, таким образом, одно- или многоканальную двухполюсную однофазную сеть передачи дискретных сообщений.

Простейшим элементом примитивной узловой сети является ветвь, представляющая собой обособленный открытый путь. Для ее описания необходимы следующие геометрические объекты: X - интенсивность потока сообщений, воздействующего на систему массового обслуживания, расположенную в ветви; N - длина очереди, возникающей в буфере системы массового обслуживания под действием входящего потока сообщений; f - интенсивность выхода обслуженных сообщений из системы массового обслуживания; является величиной, обратной времени задержки.

Согласно формуле Литтла, уравнение состояния простейшего элемента – двухполюсной однофазной сети передачи дискретных сообщений с системой массового обслуживания для узлового возбуждения – запишется как

X = f ■ N .

Геометрические объекты, необходимые для описания примитивной сети, представленные в матричной форме, имеют тот же вид, что и для элемента примитивной сети:

N = гN11 N2 ; X = X1 X2 ;f= ■ f1,1 f2,1 ... f1,2    . f2,2    . ...       . . f.,n . f2, n .. ... ... _ Nn _ ... _Xn _ _ fn ,1 fn,2 . . fn, n _ где X - интенсивности потоков сообщений, воздействующих на соответствующие ветви; N – значения длин очередей, которые возникают в буферах систем массового обслуживания, соответствующих ветвям, под действием поступающего потока сообщений; f – квадратная матрица значений интенсивности выхода обслуженных сообщений, размерностью n-строк на n-столбцов. Элементы главной диагонали представляют собой интенсивности выхода обслуженных сообщений из систем массового обслуживания в соответствующих ветвях. Остальные элементы матрицы отражают взаимное влияние систем массового обслуживания друг на друга.

Итак, матричное уравнение состояния примитивной сети:

X = f ■ N .

Эквивалентная система уравнений состояния примитивной сети:

X = f ,1 ■ N 1 + f ,2 ■ N 2 + ... + f „ ■ N_n ,

/2 = f 2,1 ■ N 1 + f 2,2 ■ N 2 + ... + f 2, n ■ N n ,

X„ = f 1- N + f 2 - N2 + ... + fn n ‘ Nn . nn , n , n , nn

Геометрические объекты, необходимые для описания исходной сети и уравнения состояния исходной сети, выраженные в матричной форме, имеют тот же вид, что и для примитивной сети, отличаясь лишь значениями компонент. Однако при соединении n отдельных ветвей в узловых сетях число независимых узловых пар уменьшается с n до ( n – k ). Независимыми называются узловые пары, которые не могут быть выражены друг через друга, в то же время любая другая величина в сети может быть получена линейной комбинацией этих независимых узловых пар. Остальные k путей учитываются при помощи уравнений связи. Геометрический объект, связывающий переменные обеих систем, называется тензором преобразования. Уравнения преобразования переменных в узловой сети имеют вид

' N 1 = A 11 ■ N ‘ + A 1,2 ■ N 2 + ... + 4, n - k ■ N ' - k ,

, N 2 = A 2,1 ■ N ‘ + A 2,2 ■ N 2 + ... + A 2, n - k ■ N n - k , (1)

, N n = A n ,1 ■ N i + A n ,2 ■ N 2 + ... + A n , n - k ■ N n — k .

Коэффициенты при величинах N исходной сети представляют собой тензор преобразования А узловой сети:

	" A 1,1	A 1,2    .	.    A 1, n - k
-A =	A 2,1 ...	A 2,2    . ...       .	.    A 2, n - k ..         ...
	_ A n ,1	A n ,2    .	. A n , n - k _

Система уравнений (1) в матричной форме запишется следующим образом:

N = А ■ N', где N – длина очередей в ветвях примитивной (вспомогательной) сети; N' - вектор длин совокупных очередей в открытых путях исходной сети; А – матрица преобразования переменных (значений длин очередей) между примитивной и вспомогательной сетями.

Выразим закон преобразования вектора интенсивностей потоков сообщений X , воздействующих на ветви примитивной сети, в вектор интенсивности потоков сообщений X' , воздействующих на узловые пары (открытые пути) исходной сети:

Х = А ■X' .                       (2)

Матрица значений интенсивности выхода обслуженных сообщений из систем массового обслуживания в исходной сети:

f ' = A T ■ f ■ A ,                    (3)

где Т означает, что матрица А транспонирована.

Следовательно, компоненты f ' исходной сети находятся по компонентам матрицы f примитивной сети с помощью формулы преобразования (3), причем размерность матрицы f ' отличается от размерности f и равна ( n - k ) строк на ( n - k ) столбцов.

Запишем уравнение состояния исходной сети в матричной форме:

X' = f '■ N '.                      (4)

Результатом решения данной системы уравнений является определение длин очередей в открытых путях (между узловыми парами) исходной сети. Обычно это лишь промежуточный результат. В том случае, если вспомогательная сеть является примитивной, длины очередей в системах массового обслуживания, расположенных в отдельных ветвях исходной сети ( N _b ) и интенсивности потоков сообщений, проходящих в отдельных ветвях ( Х' _в) находятся по формулам

N В = A ■ N ', X B = f ■ A ■ N’            (5)

соответственно.

Использование тензорной методологии для описания системы. Рассматриваемый подход дает значительное упрощение задачи описания и анализа не только сетей массового обслуживания при моделировании информационных систем, но и других задач из многих областей [5–7].

Рассмотрим схему работы систем и оборудования, являющихся составными частями системы управления предприятием макрорегионального филиала «Сибирь» ОАО «Ростелеком» (рис. 1).

Функционально данная система работает по принципу запуска и обработки запросов, с последующим предоставлением результатов. Запросами могут являться запуски выполняемых процедур обработки данных, запросы пользователей в виде получения отчетов и др. Система может не иметь возможности обработать сразу все запросы, поступившие в определенный момент времени. В этом случае образуется очередь запросов. Таким образом, система функционирует как система массового обслуживания (рис. 2).

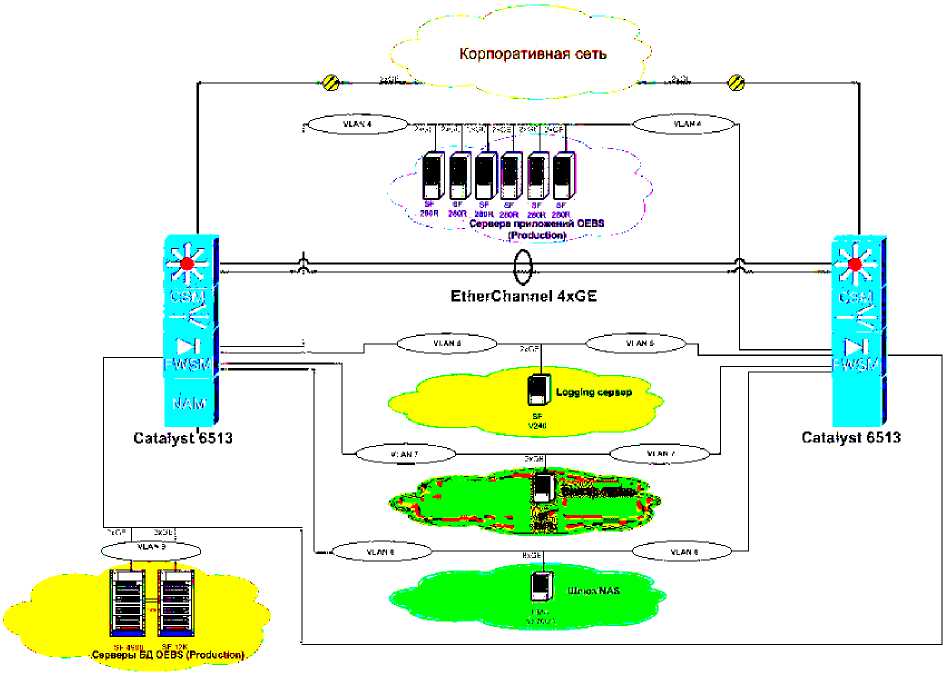
Рис. 1. Схема организации технической архитектуры системы управления предприятием

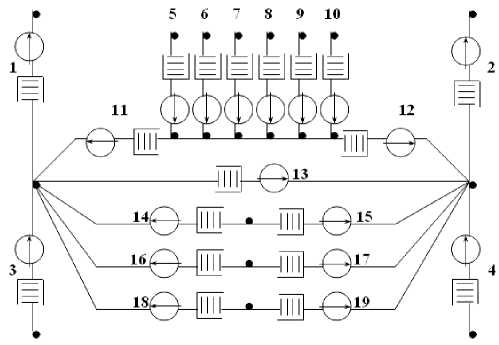
Рис. 2. Схема, представленная в виде системы массового обслуживания

С использованием тензорной методологии система описывается следующим образом:

С учетом формул (2)–(4):

N =

^X 1 ^X 2

...

^X 19

N 1

N 2

;

f1,1      0     ...0

0     f2,2   ...0

...        ...       ......

0      0     ...    f 19,19

Для анализа были выбраны следующие ветви системы:

• a :    3 13 2     c : 5 11 14     e : 7 11 18         g : 9 12 17

• b :    4 13 1     d : 6 11 16     f : 8 12 15          h : 10 12 19

Матрица тензора преобразования:

A =

A ^T

0 0 0 0 0

0 0 0 0 1 _

X 3 + X 13 + X 2 = ( ^f 3,3 + ^f 13,13 + ^f2,2 ) ■ N a + ^f 13,13 ■ N b , X 4 - X 13 + X 1 = ( ^f 4,4 - ^f 13,13 + ^f 1,1 ) ■ N b - ^f 13,13 ■ N b ,

X 5 + X 11 - X 14 = ( ^f 5,5 + ^f 11,11 - ^f 14,14 ) ■ N c +

+ ^f 11,11 ■ N d + ^f 11,11 ■ N e ,

X 6 + X 11 -X 16 = ^f 11,11 ■ N c + ( ^f 6,6 + ^f 11,11 - ^f 16,16 ) ^x

^X N d + ^f 11,11 ■ N e

X 7 + X 11 -X 18 = ^f 11,11 ■ Nc + ^f 11,11 ■ N d +

+ ( ^f 7,7 + ^f 11,11 f 18,18 ) ■ N e ,

X 8 + X 12 -X 15 = ( f 8,8 + f 12,12 - f 15,15 ) ' N f +

+ f 11,11 ■ N g + f 11,11 ■ N h,

^X 9 ^{+ X} 12 -^X 17 = f 11,11 ■ N f ⁺ ( ^f 9,9 ^{+ f} 12,12 - ^f 17,17 ) ^x

^X N g ^{+ f} 11,11 ■ N h’

• ^X 10 ^{+ X} 12 - ^X 19 = ^f 11,11 ■ N f ^{+ f} 11,11 ■ N g ⁺

• ^{+ ( f} 10,10 ^{+ f} 12,12 - ^f 19,19 ) ■ ^Nh ^.

Таким образом, мы получили систему уравнений, соответствующую формуле (4). Так же могут быть получены формулы (5) для данной системы.

Использование средств автоматизации расчета параметров. Для наглядного отображения систем и расчета характеристик часто используют специализированные программные средства. Авторами статьи разработана программа автоматизации описания систем с применением тензорной методологии (рис. 3).

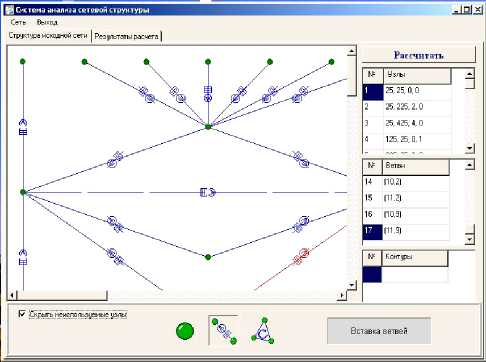
Рис. 3. Интерфейс программы анализа сетевой структуры

Программа имеет пользовательский интерфейс для составления схемы исследуемой системы. Пользователю необходимо определить узлы сети, ветви и указать последовательность обхода узлов. После окончания составления схемы необходимо нажать кнопку «Рассчитать», и программа сформирует все параметры описания системы.

Изложим результаты работ по оптимизации производительности. После проведения мероприятий 1–3, описанных выше, в том числе работ по модернизации вычислительного комплекса, необходимый результат по оптимизации производительности системы управления предприятием был достигнут (рис. 4).

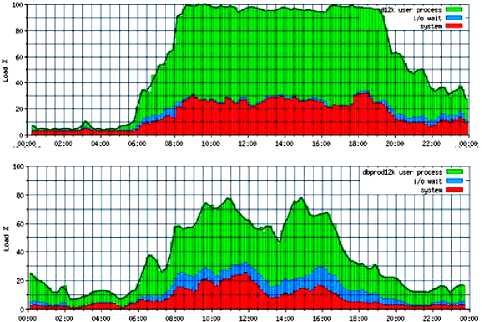
Рис. 4. Показатели загруженности системы управления предприятием до и после проведения процедур оптимизации производительности

Полученная в результате аналитического анализа и расчетов система уравнений позволила получить информацию о том, какие именно параметры системы необходимо улучшить, т. е. увеличить и перераспределить ресурсы определенных серверов, чтобы возросла производительность всей системы.

Тензорная методология является мощным инструментом для исследования характеристик сложных систем. Универсальность и общность описаний и рассуждений создает предпосылки для широкого применения методологии в современных условиях.

Представленный подход использования тензорной методологии для описания системы управления предприятием позволяет в полной мере описать систему и происходящие в ней процессы.

Использование средств автоматизации дает возможность значительно упростить рутинные операции вычисления параметров, учитывая тот факт, что система имеет сложную структуру с большим количеством элементов.