Описание упрочнения систем дислокационного скольжения за счет границ кристаллитов в поликристаллическом агрегате

Описание упрочнения материала за счет границ кристаллитов в физических многоуровневых моделях неупругого деформирования, основанных на явном введении внутренних переменных [4, 17, 18], является основной задачей данной работы. В кристаллах неупругое деформирование в основном осуществляется скольжением краевых дислокаций [3, 15], что подтверждено многочисленными экспериментальными данными. Под законами упрочнения понимаются эволюционные уравнения для критических сдвиговых напряжений на системах скольжения (СС), определяющих их изменение в зависимости от некоторого набора параметров (в этом качестве могут выступать сдвиги, скорости сдвигов, температура, энергия дефекта упаковки и т.д.) [1, 6, 10, 5]. Следует отметить многообразие физических механизмов, обусловливающих упрочнение [11-14]. В данной работе будут учтены только механизмы, связанные с взаимодействием дислокаций друг с другом и с границей кристаллита. Описание упрочнения, связанного с взаимодействием дислокаций с лесом дислокаций и образованием барьеров дислокационного происхождения, целью данной работы не является, ознакомиться с описанием упрочнения по указанным механизмам можно в работах [6-9].

Граница представляет собой двумерную специфическую область, отделяющую различные однородные части кристалла (зерна, фазы, двойники). Отметим, что межкристаллитная граница является эффективным препятствием для скользящих дислокаций. Барьерное действие границы обусловлено резким изменением ориентаций СС при переходе через нее [3]. В общем случае если дислокация текущего кристаллита перешла в соседний кристаллит со своим вектором Бюргерса, то этот вектор был бы произвольно ориентирован относительно решетки соседнего кристаллита и движение такой дислокации вызывало бы силь- ное нарушение упаковки атомов. Вследствие этого примем следующий механизм движения дислокации через границу: решеточная дислокация (РД) рассматриваемого кристаллита переходит в энергетически более выгодную СС соседнего [2], оставляя в границе дислокацию ориентационного несоответствия (ДОН). Следующая решеточная дислокация, скользящая по той же СС кристаллита, будет испытывать дополнительное сопротивление за счет поля упругих напряжений ранее образовавшейся ДОН.

Поставим задачу построения соотношения для описания упрочнения за счет границ кристаллитов, выделив несколько вспомогательных этапов: первый - определение СС в соседнем кристаллите, по которой продолжится скольжение; при этом необходимо предложить некоторый критерий, согласно которому будет определяться указанная СС в соседнем кристаллите; решение указанной подзадачи представлено в работе [2]. Второй этап носит физический характер и заключается в определении ДОН, остающейся в границе при акте прохождения дислокации через границу, и оценке напряжений, действующих на РД со стороны ДОН. Скорость возрастания этих напряжений и будет характеризовать скорость изменения критического напряжения сдвига за счет границ кристаллитов.

Таким образом, целью настоящей работы является построение и анализ закона упрочнения за счет границ кристаллитов (фаз, двойников) с использованием внутренних переменных модели (второй этап поставленной задачи). Предлагаемое соотношение должно быть приемлемо для многофазных материалов, а в его окончательное соотношение должны войти параметры мезо- и макромасштаба, имеющие ясный физический и/или геометрический смысл (для упрощения последующей процедуры идентификации модели).

1. Взаимодействие решеточных дислокаций с дислокациями ориентационного несоответствия

На основании физических соображений получим оценки барьерных напряжений, создаваемых ДОН, и сравним их с напряжениями страгивания решеточных дислокаций (напряжениями Пайерлса-Набарро), затем на основе этих оценок запишем соотношения, описывающие вклад в упрочнение, вносимый границами кристаллитов (фаз, двойников).

Отметим, что на данном этапе построения модели наибольший интерес представляют качественные зависимости скорости изменения критических напряжений по СС, обусловленных упрочнением за счет границ кристаллитов. Согласно принятому механизму прохождения решеточной дислокации (РД) на границе кристаллита появляется скопление ДОН, которое своими упругими полями препятствует движению РД рассматриваемого кристаллита. Для начала рассмотрим одну ДОН, образовавшуюся на фасетке границы кристаллитов площадью S k . Отнесем ДОН к рассматриваемому кристаллиту и положим, что среда является однородной, изотропной и упругой. Далее определим поле напряжений, действующих на РД со стороны ДОН рассматриваемой СС, затем осредним полученные напряжения по текущей плоскости скольжения. При операции осреднения необходимо задаться геометрией кристаллита (плоскости скольжения).

Заметим, что искомые барьерные напряжения т b - это касательные напряжения, действующие на краевую решеточную дислокацию в плоскости скольжения. Для их определения необходимо найти поле напряжения от ДОН о d . Будем рассматривать ДОН подобно решеточным дислокациям и относить ее к рассматриваемому (текущему) кристаллиту. Заметим, что сопротивление движению, возникающее в результате образования ДОН, вызывает лишняя экстраплоскость. Для ДОН последнюю в общем случае ввести трудно, она будет «составной». Вектор Бюргерса ДОН вполне определен разностью векторов Бюргерса решеточных дислокаций, однако вклад в сопротивление вносит составляющая, лежащая в плоскости границы , вектор Бюргерса которой коллинеарен нормали к границе. Введем ортогональный базис, связанный с ДОН. Первый базисный вектор определяется внешней нормалью фасетки границы, b d = N _k , второй l d направим вдоль линии пересечения плоскости фасетки границы N k и рассматриваемой плоскости скольжения дислокации текущего кристаллита n j 1 _d = N k x n ⁽ j ) . Третий вектор n d расположен вдоль линии пересечения плоскости границы и плоскости, построенной на векторах N _k и n :

ⁿ d = ¹ d ^{x b} d = ^N k ^{x n (} j ) ^{x N} k . ⁽¹⁾

Для оценки барьерных напряжений по отношению к движению решеточной дислокации тb, которые возникают вследствие образования ДОН на границе двух кристаллитов, будем использовать две орто- тональные декартовы системы координат (СК). Первую СК свяжем с решеточной дислокацией Ox1 x2x3 (ось Ox3 направлена вдоль оси дислокации решеточной дислокации, ось Ox1 - вдоль вектора Бюргерса, Ox2 -вдоль нормали к плоскости скольжения) (с базисом ki). Введем вторую, связанную с ДОН, СК Ox'1 x'2x'3 с базисом k 'i (ось Ox'3 направлена вдоль оси дислокации ДОН ld , ось Ox'1 - вдоль вектора Бюргерса ДОН bd, Ox'2 - вдоль нормали к плоскости скольжения nd ДОН). Зная вектор Бюргерса ДОН ЛЬ = b(,')-b(l), определим его краевую составляющую, направленную по нормали к фасетке границы:

Ь ed = ( N к •Л Ь ) N к . (2)

Отметим, что каждая дислокация обладает собственным полем напряжений, которое в силу быстрого затухания искажений кристаллической решетки при удалении от ядра дислокации можно определить, используя линейную теорию упругости. Следует учитывать, что вблизи ядра дислокации предпосылки линейной теории упругости малоприемлемы, поэтому полученными решениями можно пользоваться на определенном удалении от ядра дислокации (порядка нескольких межатомных расстояний).

Задача теории упругости о нахождении поля напряжений о d прямолинейной краевой дислокации в неограниченной среде является плоской и сводится к решению уравнения равновесия V • о _d = 0 , откуда можно определить выражения для смещений u дислокации. Для краевой составляющей ДОН в декартовой системе координат Ox' ¹ x' ² x' ³ перемещения определяются соотношениями [15]

u ₁

- b

ed

8л ( 1 - v )

x 12

⁺ x 22 ) +

x 1 - x ₂

x 12 + x 22

u 2

2л

x '

arctg — 2 +

1__x1 x2

2 ( 1 - v ) x 1 ² + x 2 ²

u 3 = 0, где v - коэффициент Пуассона. Смещение, параллельное оси дислокации, равно нулю, деформация является плоской; ненулевые компоненты тензора напряжения в рассматриваемой СК будут иметь вид [15]

[ ° d ] ' 11

^[ ° d Г 22

^Gb ed    x ^{2 ( 3} x ^{1 +} x ^{2 )}

2я ( 1 - v ) ( x 12 + x 22 )² ’

^Gb ed x^{2 (} x ¹    x ^{2 )}

2л ⁽ 1 ^{- V )} ( x 12 ₊ x *22 )

- 1 ' _    Gb ed    x ^{1 (} x ¹ x ^{2 )}

d ^{J 12} "  2л ( 1 - V ) ( x 1² + x 2² ) 2 , ^[ ° d К 33 ^ ^V (fc d 1 ' 11 ^+[ ° d 1 ' 22 )

Заметим, что для определения искомых барьерных касательных (в плоскости скольжения РД) напряжений т b необходимо перейти от компонент тензора напряжений краевой составляющей ДОН о _d в базисе k V к компонентам в базисе k i . Запишем тензор о _d в базисе k i :

о,, [о J k' k'. ,                              (5)

d d ij i j затем найдем компоненты этого тензора в базисе ki. Для этого скаляр-но умножим (5) слева и справа на векторы ki и kj:

^[ ° d ¹ j = ^k i -^[ ° d ¹ ' 1m ^k ' 1 ^k ' m ' ^k j                            ⁽⁶⁾

Компонента ' о _d ( x '1 , x ' ₂, x 3 ) ] 21 в этом базисе будет характеризовать торможение краевых решеточных дислокаций рассматриваемой СС. Разложим векторы базиса k i по направляющим косинусам базиса k V :

k 1 = cos a 1k'1 + cos p 1k'2 + cos у 1k'3, k 2 = cos a 2k'1 + cos p 2k'2 + cos у 2k'3,                  (7)

k 3 = cos a 3k'1 + cos p 3k '2 + cos у 3k'3, где на направляющие косинусы в силу единичности базисных векторов накладывается связь cos2 a 1 + cos2 p 1 + cos2 у 1 = 1, cos2 a 2 + cos2 p 2 + cos2 у 2 = 1,                     (8)

cos ² a ₃ + cos ² p ₃ + cos ² у ₃ = 1.

Здесь через a i , обозначены углы между векторами k 1 и k i ; р i - углы между векторами k ' ₂ и k i ; у i - углы между векторами k ' ₃ и k i .

Используя соотношение (6), разложение (7) и связь компонент напряжения (4), запишем искомую компоненту [ о _d ] 21 .

[ ° d 1 21 = ^k 2 ’[ ° d ] ' Im ^k ' l ^k ' m "  ^k 1 = ( cos ^a 2 cos ^a 1 ^{+ V} cos у 2 cos у 1 )^X

^X[ ° d 1 ' 11 ⁺ ( cos^P 2 cos ^a 1 ⁺ cos^a 2 cos^P 1 )[ ° d 1 ' 21 ^{+              (9)}

+ ( cos р ₂cos р 1 + V cos у ₂cos у 1 )[ о _d 1 ' ₂₂, где использовано соотношение (4)₄.

Подчеркнем, что компонента поля напряжений ДОН [ о _d ( x 1 , x '₂, x 3 ) ] 21 зависит от координат, определенных в базисе ДОН k ' i и является неоднородной: при приближении к ядру дислокации напряжения возрастают, при удалении - падают. Оценим усредненные касательные напряжения [ о _d ] , действующие на рассматриваемую плоскость скольжения решеточной дислокации. Для этого проинтегрируем напряжения [ о _d ] 21 по плоскости скольжения и отнесем их к рассматриваемой площадке. Заметим, что интегрирование удобно проводить в СК, связанной с решеточной дислокацией. Найдем связь координат радиус-вектора в СК Ox ¹ x ² x ³ и Ox' ¹ x' ² x' ³ :

r = x 1 k 1 + x ₂ k ₂ + x ₃ k 3 = x 1 k 1 + x '₂ k ' ₂ + x '₃ k ' 3 .            (10)

Отсюда, используя разложение (7), можно показать справедливость соотношения x1 = cos a 1 x 1 + cos a 2x 2 + cos a 3x 3, x2 = cos р 1 x 1 + cos р 2 x 2 + cos р 3 x 3,                 (11)

x '₃ = cos у 1 x 1 + cos у ₂ x ₂ + cos у 3 x 3 .

Примем, что кристаллит имеет форму, примерно одинаково развитую во всех направлениях (куб, шар), с характерным размером R. Положим, что плоскость скольжения решеточных дислокаций имеет форму квадрата, сторона которого пропорциональна характерному размеру кристаллита Rsl = aR. Далее будем полагать, что а порядка единицы Rsl * R .

Подставим полученные координаты (11) в соотношение для поля касательных напряжений ДОН (9) и усредним их по площади скольжения рассматриваемой СС (х2 = 0):

J E " d ( x 1 , x 3 ) ] _2id ⁵

^Т b ^_

S fd 5

S

RR j j[® d (xi,xз)]21dxidx3

_ 2 a 0

RR j JE" d (x 1, x3)] 21dxidx3

_ 2 а 0

RR

Jj d x ₁d x 3

2 a 0

R ²

.

При записи (12) учтено, что соотношения для поля напряжений от ДОН (4) приемлемо использовать на некотором удалении от ядра дислокации - порядка нескольких межатомных расстояний, параметр решетки а много меньше размера кристаллита R .

Осредненную касательную компоненту тензора напряжений ДОН (12) можно получить в аналитическом виде (например, используя пакет Mathematica). Отметим, что рассматриваемая ДОН действует своими упругими полями не только на ту СС, в результате скольжения по которой РД образовалась ДОН, но и на остальные СС решеточных дислокаций рассматриваемого кристаллита. В соотношениях при этом будут меняться направляющие косинусы базисов.

Далее оценим отношение напряжений сопротивлению сдвига решеточной дислокации, вызванной упругими полями ДОН тb, к напряжениям Пайерлса-Набарро тП-Н [15]. Напомним, что Пайерлс и Набар-ро первыми предложили расчет напряжения сдвига, необходимого для движения дислокации. Они определили изменение энергетического профиля поверхности скольжения при возникновении возмущений от движения дислокации из одного равновесного положения до другого, предполагая, что напряжение сдвига, действующее по плоскости скольжения, является периодической функцией относительно смещения соседних плоскостей. Используя синусоидальное приближение, оказалось возможным показать, что напряжение страгивания краевой дислокации определяется выражением тп-н =

2 G

1 - v

Г exp

V

2л r

( 1 - v ) b у

где G - модуль упругости, v - коэффициент Пуассона; b - модуль вектора Бюргерса; r - расстояние между атомными плоскостями в нормальном по отношению к плоскости скольжения направлении, которое может быть определено через параметр решетки а и компоненты нормали плоскости скольжения n ={ n 1 , n ₂, n ₃}:

a

r= /    —2 .      2 .      2

n 1 + n 2 + n 3

Для численной оценки отношения к т_ь /т_П-Н используем следующие параметры кристаллита (все компоненты векторов в базисе k i ):

• -    параметр решетки а = 10 ^-10 м;

• -    характерный размер кристаллита R = 10 5 м;

• -    коэффициент Пуассона v = 0,3;

• -    компоненты вектора ДОН A b = a- 3V3

  ;

  
  

• -    нормаль фасетки границы N _k = [ 123 ] .

Для примера рассмотрим кристаллиты с ГЦК-решеткой, для которых вектор Бюргерса b = a <  110 > , его модуль b = ^2- а ; плоскость скольжения определяется нормалью n ={111}.

Используя (12) и (13), определим отношение барьерных напряжений ДОН, полученной в результате взаимодействия дислокации текущей СС с границей соседних кристаллитов, к напряжению Пайерлса-Набарро данной системы скольжения. Также оценим напряжения от образовавшейся ДОН на других СС текущего кристаллита, результаты сведем в таблицу.

Анализируя таблицу, можно сделать следующие выводы:

• а)    необходимо учитывать влияние барьерных напряжений ДОН не только на текущую (рассматриваемую) СС, но и на остальные СС данного кристаллита;

• б)    барьерные напряжения ДОН значительно меньше напряжений, необходимых для страгивания краевой дислокации, но увеличение числа ДОН на границе способно сделать эти напряжения сопоставимыми;

• в)    значения напряжений ДОН на плоскости скольжения могут быть как отрицательными, т.е. способствующими сдвигу дислокаций, так и положительными - препятствующими сдвигу. При построении соотношения для упрочнения за счет границ соседних кристаллитов будем учитывать только положительные напряжения ДОН на данной плоскости скольжения дислокаций.

Отношение барьерных напряжений ДОН к напряжениям Пайерлса-Набарро

Номер СС	СС	k= т ь /т п-н '105	Номер СС	СС	k= т ь /т п-н ^10 5
1	[ 110 ] ( 111 )	15,7	13	[ 110 ] ( 111 )	–30,0
2	[ 011 ] ( 111 )	-3,14	14	[ 011 ] ( 111 )	25,0
3	[ 101 ] ( 111 )	–63,7	15	[ 101 ] ( 111 )	26,0
4	[ 011 ] ( 111 )	21,5	16	[ 011 ] ( 111 )	–7,0
5	[ 101 ] ( 111 )	–23,2	17	[ 101 ] ( 1 11 )	30,4
6	[ 110 ] ( 111 )	–6,20	18	[ 110 ] ( 111 )	11,9
7	[ 101 ] ( 111 )	–13,9	19	[ 101 ] ( 111 )	25,4
8	[ 110 ] ( 111 )	3,9	20	[ 110 ] ( 111 )	27,6
9	[ 011 ] ( 111 )	71,0	21	[ 011 ] ( 111 )	–15,9
10	[^К111 )	71,1	22	ИК111 )	10,4
11	[ 101 ] ( 111 )	–9,54	23	[ 101 ] ( 111 )	23,2
12	WO11 )	–9,96	24	WO11 )	3,63

Отметим, что в дальнейшем понадобятся коэффициенты величин упрочнения, обусловленных ДОН за счет скольжения РД по разным СС при различной взаимоориентации СС и границ. Это соотношение для модельных представлений супердислокаций, о которых речь идет ниже, получено в аналитическом виде.

На рисунке изображена характерная зависимость барьерных напряжений ДОН, действующих на СС, в результате скольжения по ко- торой РД образовалась ДОН, от размера кристаллита R, которая, как видно из рисунка, является обратно пропорциональной размеру кристаллита.

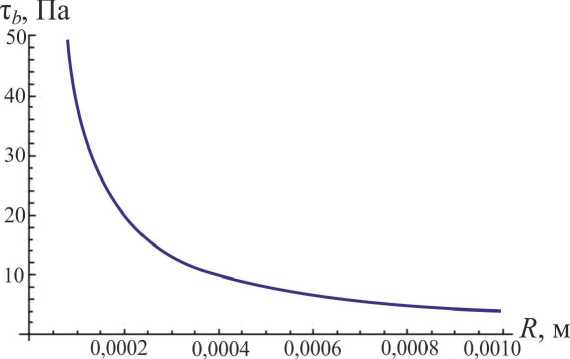
Рис. Зависимость барьерных напряжений ДОН, действующих на текущую СС, от размера кристаллита

Напомним, что согласно принятой модели прохождения краевой дислокации j -го кристаллита в l -й кристаллит образуется ДОН c разностным вектором Бюргерса A b=b ^{( ,} '⁾ - b ⁽ l) . При прохождении по той же плоскости скольжения второй дислокации образуется вторая ДОН. Другими словами, A b увеличивается до 2A b . Поэтому силы отталкивания постепенно увеличиваются, запирая данную плоскость скольжения. Заметим, что при количестве дислокаций около 10 4 -10 5 напряжения т_п-н и x b будут одного порядка.

Рассмотрим ситуацию, когда на границе данного кристаллита образуется Nd ДОН с вектором Бюргерса Ab в результате скольжения краевых дислокаций по текущей СС. Тогда ДОН Ab представим как объединенную (супер) ДОН с вектором Бюргерса AB=NdAb и, проделав аналогичные выкладки, получим барьерные напряжения т ь = (2 d) 2, = Nd ^ Д „. (15)

Заметим, что при увеличении числа ДОН на границе кристаллитов напряжения нарастают линейно.

Следует отметить, что вычисление осредненных барьерных напряжений (12) значительно усложняет дальнейшую реализацию и использование соотношения упрочнения за счет границ кристаллитов. В связи с этим будем использовать модельные представления дислока- ций, основанные на понятии супердислокации, т.е. дислокации с вектором Бюргерса, равным сумме векторов Бюргерса всех дислокаций, расположенных на каждой из рассматриваемых СС. Примем, что на границе двух кристаллитов образуется супердислокация ориентационного несоответствия (СДОН), которая своими упругими полями препятствует движению решеточных дислокаций, расположенных на рассматриваемых СС. В свою очередь, для решеточных дислокаций будем использовать представление супердислокации. В предположении, что РД распределены равномерно по плоскости скольжения, условимся, что линия решеточной супердислокации (РСД) расположена в центре плоскости скольжения. В общем случае линии РСД и СДОН не являются параллельными, а вычисление сил взаимодействия между ними также весьма трудоемко [15]. В связи с этим рассмотрим барьерные касательные напряжения Tbs, вызванные СДОН и действующие на се-

RR редину РСД r = у k 1 + у k 3:

^т bs = N d ^т d , ⁽¹⁶⁾

где т _d = [ о _d ( x 1 , x ₂, x ₃ ) ] - напряжения СДОН, действующие на середину РСД x 1 = R /2, x ₂=0, x ₃= R /2.

Закономерно возникает вопрос о сопоставлении касательных барьерных напряжений т b , полученных интегрированием (12) с напряжениями т _bs , определяемых с помощью представления супердислокаций (16). Отметим, что отношение напряжений т b /т bs для большинства СС - порядка единицы, однако для ряда СС достигает нескольких десятков. Такое несоответствие в первую очередь объясняется достаточно сложным характером интегрируемой функции касательных напряжений [ о _d ( x 1 , x ₃ ) ] 21 , для которой по теореме о среднем значении функции строится аппроксимация в центре плоскости скольжения. Вероятно, аппроксимацию надо сделать по косинусам углов, получающихся при двойном скалярном произведении направляющих диад дислокаций (нормаль и вектор Бюргерса), и размеру кристаллита.

Подчеркнем физическую прозрачность представления, основанного на использовании понятия супердислокаций, поэтому далее для упрощения процедуры нахождения барьерных напряжений, вызванных ДОН, будем использовать напряжения тbs. Напомним, что речь идет о поиске качественной зависимости барьерных напряжений. В дальнейшем (для количественных расчетов) в соотношениях для критических напряжений вводятся параметры, определяемые в ходе процедуры идентификации.

Перейдем к завершающему этапу поставленной задачи - формулировке соотношения для составляющей скорости изменения критического напряжения скольжения за счет зернограничного упрочнения, используя внутренние переменные модели.

Условимся, что каждая решеточная краевая дислокация, достигающая границы кристаллита, образует ДОН, если только кристаллиты идеально не сопряжены. Поэтому примем следующую гипотезу: количество ДОН N d пропорционально количеству мобильных дислокаций, прореагировавших с границей . Последнее, в свою очередь, согласно соотношению Орована пропорционально величине сдвига у ⁽ j ⁾ по рассматриваемой СС с учетом геометрии фасеток кристаллита. В первом приближении примем, что данная геометрическая зависимость характеризуется отношением площади части границы S k (фасетки границы), пересекаемой рассматриваемой СС, ко всей площади границы S текущего кристаллита и мерой разориентации СС текущего и соседнего кристаллита £ ( jm ) . Напомним, что мера разориентации ^ ( j m ) определяется из условия минимизации скорости приращения внутренней энергии соседних кристаллитов в текущий момент деформирования [2]. Тогда скорость добавочного критического напряжения сдвига т ( j^ ) , обусловленная ДОН, для данной j -й СС рассматриваемого i -го кристаллита, взаимодействующей с m -м кристаллитом через к -ю фасетку границы, запишется в виде

у (j ’к )_ n S к ^( j,к )•(j) (j, j)

^т ( i , m ) ^— 'I s Ч ( i , m ) I ^т bs ’ ^(1/) где т bs ’ j ) - положительная компонента касательных барьерных напряжений, действующих на РД j -й СС со стороны ДОН, образованных в результате скольжения дислокаций по j -й СС (определяется соотношением (16)); у ⁽ j ⁾ - скорость сдвига по j -й CC; । - безразмерный параметр, определяемый в ходе процедуры идентификации модели.

Напряжения, препятствующие движению решеточных краевых дислокаций, вызваны касательными напряжениями от ДОН. Отметим, что напряжения ДОН, образовавшейся в результате скольжения по текущей СС, могут оказывать достаточно сильное сопротивление сдвигу по другим СС (см. таблицу). В связи с этим будем учитывать касательные барьерные напряжения от всех ДОН, образовавшихся к данному моменту и препятствующих сдвигу по рассматриваемой СС. С учетом последнего замечания скорость барьерных напряжений ДОН т ( vm ) для данной j -й СС рассматриваемого i -го кристаллита, взаимодействующей с m -м кристаллитом через k -ю фасетку границы, запишется в виде

K

^{( j} , k )    ^rk y <' s , ^k )у ( s )_т^{( j} , s )

^Т ( i , m ) ⁴ q / S ( i , m ) Г ^T bs ,                             ^(1O)

^ s-I где т js) - положительная компонента касательных барьерных напряжений, действующих на РД j-й СС со стороны ДОН, образованных в результате скольжения дислокаций по s-й СС.

Соотношение (18) описывает скорость изменения критического напряжения за счет взаимодействия решёточных дислокаций с k -й фасеткой границы. Суммируя скорость барьерных напряжений ДОН по всем фасеткам границы k - 1, K f (одновременно по соседним кристаллитам m ) и опуская в левой части индекс текущего кристаллита i , из (18) получим

Kf            Kf

+ (j) _у(j•k)-nV^kV?(s•k)y(s)T(j.s)(IO)

ТЗГУ / , T (i,m) 'I/      / S (i,m) I т bs '

k - 1                k - 1 ^ s - 1

Размер кристаллитов (зерен) оказывает заметное влияние на неупругое поведение поликристаллических материалов. Количество дислокаций в скоплении у границ кристаллитов непосредственно зависит от длины свободного пробега дислокации, которая определяется размером зерна. В связи с этим при уменьшении зерна кривая диаграммы нагружения заметно смещается в область более высоких напряжений [16]. Из экспериментальных результатов известно, что плотность дислокаций растет с ростом деформации; тогда, если предположить, что для обычных поликристаллов (с размером зерна от 10 до сотен мкм) плотность дислокаций растет примерно одинаково в процессе деформирования, ясно, что образование зернограничных барьеров будет ид- ти быстрее в материалах с меньшим размером зерна. Проанализировав получившуюся формулу (19), увидим, что скорость напряжений т 3(у обратно пропорциональна характерному размеру кристаллита, поскольку такую зависимость имеет множитель т (sjs). Аналитическая зависимость барьерных напряжений т js), получаемая при рассмотрении СДОН и РСД, имеет вид

т

(j, s) bs

b'd ⁾ G

(л R ( - 1 + v)((cosa ⁽ j ^{, s} ) + cos у ⁽ j ^{, s} ) ) ² + (cos a 2 j ^{, s} ) + cos у 2 j ^{, s} ) ) ² ) ²

x

x { - cos a ⁽ j ^{, s} ) ⁴ cosp 2 j ^, s ) + cos a ⁽ j ^{, s} ) ⁴ cosp 2 j s ) + cos a ^j s ) ³ (2v cos a 3 j ^{, s} ) x x cosp 3 j , ^s ) + cosp ⁽ j ^{, s} ) cosу ⁽ j ^{, s} ) + 3cosp 2 j^s ) cos у 2 j ^, s ) ) + 2 v cos a 3 j ^{, s} ) x x cosp 3 j , s ) cos у 2 j ^, s ) (cos у ⁽ j ^{, s} ) ² + cos у 2 j ^, s ) ² ) + cos a ⁽ j ^{, s} ) ³ ( - 3cosp 2 j ^, s ) x x cos у ⁽ j ^{, s} ) + cosp ⁽ j ^{, s} ) (2cos a ^js ) + 3cos у 2 j^s ) )) + cos a 2 j^{s )2} (2(3v cos a 3 j ^{, s} ) x x cosp 3 j ^, s ) + cosp ⁽ j ^{, s} ) cos у ⁽ j ^{, s} ) )cos у 2 j , s ) - cosp 2 j , ^s ) (cos у ⁽ j ^{, s} ) ² - 3cos у 2 j ^{, s} ) ² )) + + cos a ⁽ j ^{, s} ) ² (2( v cos a 3 j ^{, s} ) cosp 3 j ^{, s} ) + 3cosp ⁽ j ^{, s} ) cos у ⁽ j ^{, s} ) )cos у 2 j^s ) + + cos a 2 j^s ) (2v cos a 3 j , ^s ) cosp 3 j ^{, s} ) + 3cosp ⁽ j ’ ^s ) cos у ⁽ j ’ ^s ) + cosp 2 j , ^s ) cos у 2 j ’ ^s ) ) + + cosp ⁽ ₂ j ’ ^s ) ( - 3cos у ⁽ j ’ ^s ) ² + cos у 2 j , ^s ) ² )) + cos a 2 j ’ ^s ) ( - (cosp ⁽ j ’ ^s ) cos у ⁽ j ’ ^s ) + + cosp ⁽ ₂ j ’ ^s ) cos у 2 j , ^s ) )(cos у ⁽ j ’ ^s ) ² - cos у 2 j ’ ^s ) ² ) + 2v cos a 3 j , ^s ) cosp 3 j ’ ^s ) x x (cos у ⁽ j ’ ^s ) ² + 3cos у 2 j , s ) ² )) + cos a ⁽ j ’ ^s ) (2cos a 2 j , ^s ) ³ cosp ⁽ j ’ ^s ) + cos у ⁽ j ’ ^s ) x x (4 vcos a 3 j , s ) cosp 3 j ’ s ) + 3cosp ⁽ j ’ ^s ) x cos у ⁽ j ’ ^s ) )cos у 2 j ’ s ) + cosp ⁽ j ’ ^s ) x x cos у 2 j , s ) ³ + cos a ⁽ ₂ j ’ ^s ) ² ( - cosp 2 j ’ ^s ) cos у ⁽ j ’ ^s ) + 5cosp ⁽ j ’ ^s ) cos у 2 j , ^s ) ) + + cosp 2 j , ^s ) cos у ⁽ j ’ ^s ) ( - cos у ⁽ j ’ ^s ) ² + cos у 2 j ’ ^s ) ² ) + 4cos a 2 j ’ ^s ) x x ( v cos a 3 j ’ ^s ) cosp 3 j , ^s ) cos у ⁽ j ’ ^s ) + cosp ⁽ j ’ ^s ) cos у 2 j , ^s ) ² ))))}.

Заключение

Рассмотрена задача описания упрочнения систем скольжения дислокаций за счет границ кристаллитов, определена составляющая скорости критических напряжений, обусловленных влиянием границ соседних кристаллитов. В результате несовместности СС соседних кристаллитов на границе появляются ДОН, которые своими упругими полями напряжений препятствуют движению решеточных дислокаций в зерне. Путем отнесения ДОН к рассматриваемому кристаллиту были получены качественные оценки этих напряжений, действующих на РД в упругой изотропной среде, основываясь на которой, были записаны соотношения для определения указанной составляющей скорости изменения критических напряжений с использованием внутренних переменных модели.

Работа выполнена при поддержке РФФИ (гранты №10-08-00156-а, №10-08-96010-р_урал_а, №12-08-01052-а, 12-01-31094 мол_а), ФЦП «Научные и научно-педагогические кадры инновационной России на 2009-2013 годы» (мероприятие 1.2.2, Соглашение 14.B37.21.0382).