Описание вязкоупругости полимерных материалов статистическим методом
Автор: Рымкевич Ольга Васильевна, Рымкевич Павел Павлович, Романова Алла Александровна
Журнал: Технико-технологические проблемы сервиса @ttps
Рубрика: Методические основы совершенствования проектирования и производства технических систем
Статья в выпуске: 1 (23), 2013 года.
Бесплатный доступ
Предложено описание вязкоупругости полимерных материалов, используемых для защиты автомобильных деталей, статистическим методом. Получено уравнение, позволяющее описать режимы деформации в различных температурных полях.
Термоусаживающаяся трубка, эффект памяти формы, вязкоупругость, коэффициент продольной и поперечной усадки
Короткий адрес: https://sciup.org/148186053
IDR: 148186053 | УДК: 677.017.56
Текст научной статьи Описание вязкоупругости полимерных материалов статистическим методом
Автомобильные детали со сложным профилем в режиме эксплуатации подвергаются негативным воздействия окружающей среды. Поэтому очень важно для повышения их износостойкости, а также для улучшения изоляционных свойств защищать их специальными термоусаживающимися трубками. Эти трубки изготавливаются из, так называемых, ”умных материалов” – материалов с эффектом памяти формы [1 – 2]. Такие материалы под действием температурного поля усаживаются, возвращаясь к своим первоначальным размерам, обеспечивая деталям со сложным профилем герметичную защиту. Выбор оптимального температурного воздействия для обеспечения термоусадки изделий является актуальной задачей.
Целью данной работы является разработка метода, позволяющего вывести уравнение для расчета коэффициент усадки термо-усаживающейся трубки в различных температурных режимах.
Разобьем всю структуру полимерной нити на множество сегментов макромолекул [3
– 7] Будем называть такие сегменты кластерами, которые могут находиться в двух основных энергетических состояниях. Состояние 1 соответствует нити перед ее вытяжкой при температуре, близкой к температуре плавления, и является наиболее энергетически выгодным, состояние 2 – состояние, которое занимает структура после охлаждения. На рисунке 1 изображена зависимость внутренней энергии U кластера от его линейных размеров
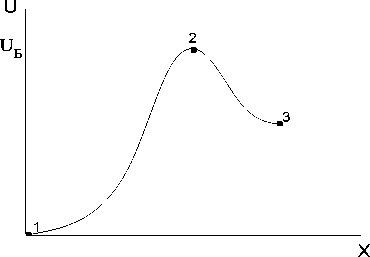
Рисунок 1. Зависимость внутренней энергии U кластера от его линейных размеров
Проведем исследование в обратимой области деформации. Найдем вероятность перехода кластера W13 в единицу времени в результате тепловых флуктуаций из состояния 1 в состояние 3. Вероятность данного перехода - Ul пропорциональна e kT . Обозначим коэффициент пропорциональности за v0 и примем, что
UБ = U12 и UБ - U3 = U32 . С Учетом этого вероят- ность W13 paʙʜa:
- U n
W, = V e kT .
Аналогично , вероятность обратного перехода W 31 можно представить как:
_ U» W, = VekT .
Перейдем к приведенным значениям энергий, т.е. к энергиям, отнесенным к абсолютной температуре. Приведенные величины будем обозначать надстрочным символом – звездочка. Тогда :
*
W 13 = v о e - U ”; (3)
*
W 31 = v 0 e ’2 . (4)
В условиях, когда система находится в деформированном состоянии, кластеры обладают еще и упругой энергией. Так как упругая энергия пропорциональна а ,то механическое напряжение играет активирующую роль. Оно понижает барьер, т.е. способствует переходу 1 – 3 и повышает наоборот барьер в направлении 3 – 2 на величину упругой энергии. Все переходы в напряженном состоянии будем обозначать символом ”~”. С учетом вышесказанного:
*
и 12 = U 12 - Y X 2 ; (5)
*
U 32 = U 32 + Y X , (6)
* 1
где y--и является структурночувствитель-T ным коэффициентом, зависящим от рода нити.
В напряженно-деформированном состоянии вероятности переходов 1 – 3 и 3 – 1:
*
W 13 = V о e - U ”; (7)
W 31 = V 0 e - U ”. (8)
Составим уравнение, отражающее закон сохранения общего числа кластеров с учетом двух возможных устойчивых состояний;
z^z z^z z^z Z^Z z^z dN3 = W13 dtNi - W31 dtN3;
z^z z*e»Z z^z z*e»Zz^z dNi = W31 dtN3 - W13dtN 1;
z^Zz^Z d (N 3 + N,) = dN0 = 0,(11)
где: dN3 - изменение числа кластеров в состоянии 3 за единицу времени; dN1 – изменение числа кластеров в состоянии 1 за единицу вре- мени; N0 – начальное число кластеров.
Рассмотрим образец синтетической нити с первоначальной длиной L 0 . В состоянии 1 находится число кластеров равной N 1 с длиной a , в состоянии 3 – N 3 с длиной b .
Назовем b - a = 5 - квантом деформации.
-
Введем число кластеров n 4 с длиной c . N 4 – число кластеров, которые дают остаточную деформацию.
Так как время жизни макромолекул на вершине барьера в состоянии 2 мало, их числом можно пренебречь. Тогда первоначальная длина образца равна:
L 0 = N 1 a + N 3 b + N 4 c . (12)
При деформировании (растяжении) образца число кластеров в состоянии один – N 1 , а в состоянии 3 – N 3 . Число кластеров в состоянии N 4 остается неизменным. Длина образца L при приложении нагрузки:
L = T V 1 a + T V 3 b + N 4 c + L 0 x , (13)
где L 0 x – упругая часть.
Найдем абсолютное удлинение
A L = ( T N 1 - N 1 ) a + ( T N 3 - N 3) b + L 0 x (14)
Вычислим относительную деформацию, поделив уравнение (14) на L 0 :
ab
£ = X + — ( N 1 - N ) + — ( N 3 - N ) (15) L 0 L 0
ab
Часть —( N 1 - N ) + — ( N 3 - N ) пред- 13
L 0 L 0
ставляет собой конформационную часть деформации £ К о Нф .
Продифференцируем уравнение (15) по времени, воспользуемся формулами (9) и (10) и учтем, что (W31 TN3 — W13 TN 1) и отличаются только знаком. В
*^v ^v ( W 13 N 1
—
*^v ^v
W 31 N 3 )
Z^Z
5 N i
следующее выражение:
d
— (s — x ) = dt
b — a
L 0
...
итоге получим
1“ z^z ^w ^^ rw ^^
|_ W 13 N 1 — W 31 N 3 ] = ...
^ W 13 N 1 — W 31 N 3 ] .
Так как
Z^Z Z^Z
N 1 + N 3 = N 0 ;
z^z
z^z
N 3 = N 0 — N1, то уравнение (16) преобразуется к следующему виду:
d 5 г ~ ~ ~ ~ ~ 1
— ( s — x ) = — I w 13 N 1 — W 31 N + W 31 N 1 1 = ...
dtL 0 0
...
= —I ( W 13 + W 31 ) N 1 L о L
—
W 31 N 0 ] .
В стационарном состоянии левая часть уравнении (18) обращается в ноль. Состояния можно считать стационарными, так как вследствие малой скорости деформации переходы в кластерах успевают отрелаксировать быстрее, чем происходит растяжение. Тогда:
(W 13 + W 31 ) N 1 — W 31 N 0 = 0;
( W 13 + W 31 ) T N 1 = W 31 N 0 .
Отсюда находим число находящихся в состоянии 1, для
кластеров,
образца
в
напряженно-деформированном состоянии.
^*v
N 1 = N 0
W 31
z^z z^z
V W 13 + W 31 J
.
Аналогично, число кластеров, находя-
щихся в состоянии ного образца равно
1 и 3, для недеформирован-
|
N 1 |
= N 0 |
V W 13 + W 31 J |
; (21) |
|
N 3 |
= N 0 |
( w Л |
. (22) |
13 31
Перепишем уравнение (15) , учитывая уравнение (17):
^w
5 N i
L 0
bN 0 L 0
—
( s — x )--( aN , + bN ) .
L 013
Подставим в уравнение (23) выражения (21) и (22):
L 0
— ( s — x ) +
N о 5 W 31
L 0 ( W 13 + W 31 )
.
N
Обозначим — = m , где m
L 0
–
число
кластеров на единицу длины, т.е. линейная плотность кластеров. С учетом m 0 уравнение (24) привет вид:
для W 13
U 3*2
—
для
AZ
5 N i
L 0
...
m 5 W
— ( s — x ) + 0 WX3 + W 31
mn 5
— ( s — x ) + —0—
W
- +1
TV
.
...
.
Подставим в уравнение (25) выражения и W 31 из уравнений (3) и (4) и учтем, что
U 21 =— U 3 :
Z^Z
5 N 1
*
*
L 0
— ( s — x ) +—
e
m 0 5
— I
*.
U 3 + 1
Подставим в уравнение (18) выражение из уравнения (25):
L 0
d
— ( s — x ) = dt
m 0 5
— ( s — x ) + •
— U, e ’ +
( W 13 + W 31 )
—
5 W 31 N
.
L 0 (27)
N
Учитывая, что — = m
L 0 преобразований уравнение ином виде:
0 и после ряда
(27) перепишем в
d ( s — x ) ~
—----- + ( W 13
dt
ZV
+ W 31 )( s — x ) = m 0 5
>—■/ >—■/
W 13 + W 31
*
e — U 3
ZV
— W 31
...
m о 5
*
.— U 3
...* 13 31
e — U 3 + 1 L
Обозначим I = ^ W 13 —
W 31 e — U ’ ] и рассмотрим
отдельно, учитывая уравнения (5) – (8), а также равенство U3*2 + U3* = U* :
Z^Z
W 13
—
*
W 31 e U -
* *2
: 12 + Y x — e
—(
*7
-U 32 — Yx
—
*
■ U 3 ) = ...
* *2 *2
... = v 0 e — U 2 (e Y x — e — Y x ).
Def e z
Учитывая, что по определению shZ = —
гиперболический синус, то
— z
— e
-
в виде:
* 2 Def Y x
* 2 e sh Y x = ---
- e
* 2
Тогда уравнение (29) можно переписать
*
I = 2 v 0 e 12 sh ( y x )
Учитывая выше сказанное:
d ( е - x )
dt
+ v 0 е
-(
,, * * 2
- U y x *
12 (e + e
1 • 2
, U 3 - Y x
)( е - x ) = ...
...
2 m 0 8
- U * 1
e 3 + 1
V 0 е
-
*
12 sh ( y x ).
Пусть 0 =— - время релаксации, т.е. W 2
ет описать различные режимы деформирования, в частности, процесс термической усадки. Условия термической усадки:
ст = const = 0; T = f ( t ) .
При условии x = 0 уравнение (35) переписывается в виде:
d E
— + (1 + A ) е = 0 , (36)
dT где eU3 = A .
Уравнение (36) - это дифференциальное уравнение с разделяющимися переменными. t
Здесь т = —, где t - время выдерживания об-0
среднее время прохождения системы через потенциальный барьер в состоянии при отсутствии нагрузки. С учетом того, что W2 = v0 e-U12 , получаем выражение для времени релаксации:
-
1 *
0 - e U 12 .
p
V 0
Введем новое безразмерное время прохождения через барьер, которое будет выра- жаться в долях от времени релаксации 0р, и зависящее от температуры т = —. (34)
0 p
-
2 тп8
Пусть выражение —-— = х f ( T ) , где e - U 3 + 1
X f ( T ) - безразмерный параметр, являющийся функцией температуры.
Произведение т 0 8 показывает максимальную деформацию, вызванную конформационными переходами.
Параметр x f ( T , - это максимальная деформация, вызванная конформационными переходами при определенной температуре. С учетом x f ( T ) уравнение (32) можно переписать в виде:
— ( е - x ) + ( е - x )(e Y x + e U 3 - Y x ) = x sh ( Y x 2). (35) d T
Уравнение (35) работает при гипотезе о независимости кластеров друг от друга, т.е. при отсутствии корреляции. Таким образом, в рамках предложенной модели было получено определяющее уравнение (35).
Обыкновенное нелинейное дифференциальное уравнение 1- го порядка (35) позволя- разца в печи. При этом выполняется условие: при т ^», е ^ е нас
Приведем решение уравнения (36):
е = е _ [ 1 - e - ] (37)
Уравнение (37) с достаточной точностью соответствует экспериментальным данным по усадке мононити из модифицированного полиолефина, комплексной полиэтилентерефталатной нити и текстильного полотна, состоящего из слабоусаживающейся основы в продольном направлении и указанных мононити и комплексной нити в поперечном направлении в диапазоне температур 115 - 200 0 С [8]. Продольная усадка мононити и комплексной нити приводит к усадке полотна в поперечном направлении. В частности, можно привести зависимость деформации от времени для указанных систем при 150 0 С. На рисунках 2 - 4 приведены экспериментальные и теоретические зависимости коэффициента продольной деформации е прод,% от времени выдерживания в печи для мононити, комплексной нити и текстильного полотна соответственно, а также указаны соответствующие дифференциальные уравнения с их решениями.
Предложенная статистическая модель в достаточной степени точности описывает процесс усадки различных полимерных систем при воздействии температуры. Данная модель применима не только к “простым” моделям - мононити, комплексной нити, но и к более сложным конструкциям, в частности, к текстильному полотну. Возможность применения статистической теории обусловлена хорошей согласованностью с экспериментом в широком диапазоне температур 115 - 200 0 С.
епрод ,% 100
епрод, %
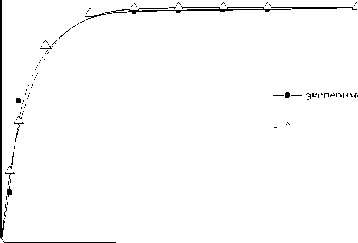
эксперимент теория

t, мин
t, миʜ
Рисунок 2. Зависимость коэффициента продольной деформации мононити от времени выдерживания в печи при температуре 150 0С: 1 – эксперимент; 2 – теория
Рисунок 4. Зависимость коэффициента поперечной деформации полотна от времени выдерживания в печи при температуре 150 0С: 1 – эксперимент; 2 – теория
— + 0,76 s = 0; s = 50(1 - e 0,76 t ) dt
— + 0,73 s = 0; s = 87,5(1 - e 0,73 t ) dt
е прод, %
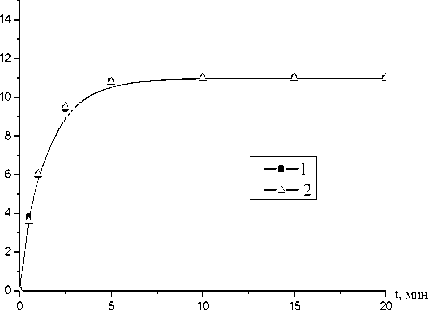
Рисунок 3. Зависимость коэффициента продольной деформации комплексной нити от времени выдерживания в печи при температуре 150 0С: 1 – эксперимент; 2 – теория
de
— + 0,8 s = 0; e = 11(1 - e dt ,
0,80 t )


