ОПИСАНИЕ ЗЕРНА МОДЕЛЬЮ СЛУЧАЙНО-НЕОДНОРОДНОЙ ОПТИЧЕСКОЙ СРЕДЫ С ЦЕЛЬЮ МЕЖЛАБОРАТОРНОГО СОГЛАСОВАНИЯ ИЗМЕРЕНИЙ ПОКАЗАТЕЛЯ СТЕКЛОВИДНОСТИ

Вопросам автоматизации органолептических измерений сейчас уделяется большое внимание. В частности, публикуются исследования о возможностях различных методов оценки стекловид-ности зерна. Авторы работ получают результаты, показывающие техническую возможность определять стекловидность методами ИК спектроскопии [1], техническим зрением [2], рентгенографией [3], спектроскопии в видимой области [4]. Компанией "Экан", в свою очередь, предлагается метод оптико-компьютерной диагностики, реализованный на базе диафаноскопа "Янтарь". Метод доказал свою состоятельность в задаче рутинного анализа стек-ловидности в лабораториях [5]. Т.е. задачу автоматизации процедуры анализа на данный момент можно считать решенной. Следующая актуальная проблема, которая возникает при использовании инструментальной объективной оценки стекло-видности, заключается в обеспечении единства измерений в разных лабораториях.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Для решения практической задачи целесообразно дать определение стекловидности в технических терминах, т.к. существующее определение дано для зрительного восприятия человека [6]. Когда говорят о стекловидности, имеют в виду соотношение мучнистого и стекловидного эндосперма зерна. Именно количество мучнистых вкраплений в значительной степени определяет технологические свойства зерна. С точки зрения оптики стекловидный эндосперм можно описать как однородную прозрачную среду с постоянным коэффициентом преломления. Эндосперм мучнистого зерна можно смоделировать порошком с частицами случайной формы. Т.е. в стекловидном зерне ослабление потока падающего света происходит только за счет процесса поглощения, а в мучнистом — за счет процессов рассеяния и поглощения. Таким образом, стекловидность зерна предполагается оценивать с помощью характеристики рассеяния (больше рассеяние — меньше стекловидность, см. рис.).

Для оценки характеристики рассеяния нужно отметить, что в данном случае речь идет об объемной доле рассеивающих частиц от 0% (абсолютно стекловидное зерно) до 100% (абсолютно мучнистое зерно); освещение образца зерна применяется диффузное. В таких условиях для численной оценки коэффициента рассеяния рационально применить теорию Кубелки и Мунка [7]; [8]. В данной теории поток проходящего излучения для конечной среды описывается уравнением:

F ( т ) = C 1 e a + C 2 e - ^{a T} ,              (1)

где F — поток излучения, τ — оптическая длина, C 1 , C 2 — постоянные коэффициенты.

a = jK ( K + 2 S ) ,                (2)

где K — коэффициент поглощения, S — коэффициент рассеяния.

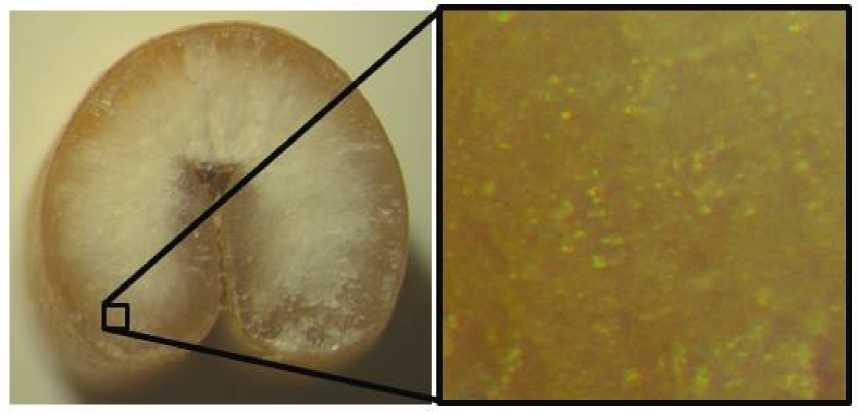
Рассеивающие мучнистые частицы в зерне пшеницы

Коэффициенты C 1 , C 2 вычисляются экспериментально один раз. При определении стекловид-ности пробы фактически необходимо вычислить K и S . Для оценки степени стекловидности каждого зерна при анализе на нескольких длинах волн ( λ 1 , λ 2 , …, λ N ) можно записать систему уравнений

F ( * ) = C e 'jK i ⁽ K i ^{+ 2 S} i ) + C e ~^Ti ^K i ⁽ K i ^{+ 2 S} i )

, ^T i V K N ⁽ K N ^{+ 2 S} i )              ^T i V K N ⁽ K N ^{+ 2 S} i )

F i N ^{( T} i ) = C i N e            ⁺ C 2 N e             ,

* m ^K i ⁽ K i ^{+ 2 s}m )           ^{- t} m Ki ⁽ K i ⁺ 2 ^sm )

F M i ^{( T} M ) = C ii e            ⁺ C 2i e            ,

[ F ( t ) = C i N e

, T^ K n ( K n + 2 S )           -T^ K n ( K n + 2 S )

•             ⁺ C 2 N e             ,

p /    \ _ v^ ^TT M 7 K N ⁽ K N ^{+2 S}M ) | Г2 ^-T M K N ( ⁽ K N ^{+2 S}M )

_ F MN ^{( T} M ) = C i N e            ⁺ C 2 N e

.

где K 1 , K 2 , …, K N — коэффициенты поглощения на длинах волн λ 1 , λ 2 , …, λ N .

При этом если длины волн падающего излучения близки и много меньше размера рассеивающих частиц, то можно сделать допущение, что коэффициент рассеяния S одинаков для всех длин волн.

Предполагается, что стекловидность зерна пропорциональна S .

Второе допущение состоит в том, что все зерна одной пробы имеют одинаковый коэффициент поглощения на N- й длине волны (одинаковый "цвет").

Пользуясь вторым допущением, можно записать общую систему уравнений для всей пробы из M зерен:

При решении системы уравнений (4) вычисляются коэффициенты S 1 , S 2 , …, S M , характеризующие стекловидность зерен 1, 2, …, M .

Для того чтобы согласовать измерения на нескольких приборах, необходимо измерить начальный световой поток F (0) = F 0 (разный для каждого прибора). Прямое измерение не всегда возможно, т.к. величина F 0 превышает световой поток после прохождения зерна более чем на порядок. Поэтому для измерения F 0 предлагается предварительно ослабить световой поток с помощью эталонных образцов с нулевым рассеянием. При наличии двух таких эталонов разной толщины t 1 и t 2 с одинаковым коэффициентом поглощения K , пользуясь законом поглощения Бугера— Ламберта—Бера, можно записать систему уравнений

F =Fe ^{- Kt} i

R i       0 e      ,

Тогда

K =-in (FR 2/ FR,) ,(6)

t 2 t 1

F = -F1- = F-,(7)

0   e~ Kti    e~ Kt 2'

где F R 1 — световой поток после прохождения первого эталона, F R 2 — световой поток после прохождения второго эталона, K — коэффициент поглощения эталонов.

Для учета разного начального светового потока приборов предполагается найти связь между F 0 и коэффициентами C 1 , C 2 таким образом, чтобы вычисленные на разных приборах значения S 1 , S 2 , …, S M из системы (4) были одинаковы.

ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ

Практическая реализация проводилась на базе диафаноскопа "Янтарь" производства фирмы "Экан". Принцип работы диафаноскопа заключается в просвечивании пробы зерна равномерным диффузным световым потоком в видимой области спектра с дальнейшим получением цифрового изображения, его программной обработкой и выдачей результата определения стекловидности. Суть предварительной программной обработки, связанная с сегментированием и коррекцией яркости изображения, изложена в [5].

В качестве меры светового потока F, прошедшего через зерно, используется его средняя скорректированная яркость [5]. В качестве оценки оптической длины τ принимается ширина проекции изображения зерна, т.к. существует связь между линейными размерами зерна. Для оценки коэффициентов C1, C2 был поставлен эксперимент. Были взяты 20 образцов зерна с разной стекловидно-стью, разных сортов, регионов произрастания. Для каждой пробы было записано и численно решено уравнение (4). Анализ результатов вычисления т. K (K +25)

показал, что слагаемое C ₁ e вносит несущественный вклад в оцениваемый световой поток F . Поэтому для практического применения рационально упростить модель и считать C 1 = 0. Тогда

F ( 0 ) = C 2 = F o , (8)

F ( т ) = F _o e "^т K ⁽ K +2 ⁵ ) . (9)

Также расчет показал, что для оценки коэффициента рассеяния целесообразно использовать яркость красного и зеленого каналов RGB-камеры. Коэффициент поглощения зерна для синего цвета значительно больше коэффициента рассеяния, по- этому включение дополнительных уравнений для синего цвета не улучшает результат вычислений.

Таким образом, система уравнений (4) принимает вид

R 1 ( w ) = R ₀ e ~ w^K R ^{( Kr} + 2 ^{5 1} ) ,

G 1 ( w 1 ) = G ₀ e ~ w^K G ⁽ K ^G + 2 ^{5 1} ) ,

•   :

D        A — D - - w M K R ⁽ K R ^{+ 2 5} M )

RM ( wM ) = R0e,

\        - w M K G G ^{( K} G + 2 ⁵ M )

I GM ( wM ) = G0e, где Ri, Gi, i = 1, 2, …, M — оцененный световой поток, прошедший через i-e зерно для красного и зеленого каналов соответственно; wi, i = 1, 2, …, M — ширина проекции i-го зерна; R0, G0 — оцененный начальный световой поток для красного и зеленого каналов соответственно.

Оценка коэффициентов рассеяния зерна на конкретном приборе сводится к измерению начальных световых потоков R 0 , G 0 и численному решению системы уравнений (10). Физический смысл использования уравнений для двух длин волн заключается в компенсации разного цвета зерна. Например, одинаковую математическую модель можно использовать для оценки стекловидности как краснозерной, так и белозерной пшеницы.

Для измерения F 0 на разных приборах используются эталоны на основе двух нейтральных светофильтров. Все светофильтры изготовлены из одной пластины, поэтому имеют одинаковый коэффициент поглощения. Периодически эталон устанавливается в прибор, и программа оценки сохраняет значение F 0 для красного и зеленого каналов. Далее в ходе работы для пробы зерна строится система уравнений (10). В ходе решения вычисляются S 1 , S 2 , …, S M , характеризующие стек-ловидность зерен 1, 2, …, M .

АПРОБАЦИЯ

Впервые такой подход был апробирован на базе ФГБГУ "Россельхозцентр". В составе организации находятся 14 филиалов, оснащенных диафаноскопами "Янтарь". Филиалы расположены на большом удалении друг от друга, поэтому идея согласования измерений стекловидности без транспортировки калибровочных образцов зерна актуальна. Диафаноскопы были оснащены идентичными эталонами и программным обеспечением, реализующим оценку стекловидности описанным способом. Далее были проведены межлабораторные сличительные испытания (МСИ). В качестве критерия

Результаты МСИ

Номер участника	Z (стекловидность) для твердой пшеницы	Z (стекловидность) для мягкой пшеницы	Оценка результатов измерений
1	1.0	–0.5	Удовл.
2	–1.5	0.9	Удовл.
3	–0.8	0.7	Удовл.
4	–1.2	0.4	Удовл.
5	–1.3	1.0	Удовл.
6	1.2	1.1	Удовл.
7	0.4	0.8	Удовл.
8	0.9	–0.4	Удовл.
9	0.2	–1.3	Удовл.
10	0.4	–1.7	Удовл.
11	0.9	–0.1	Удовл.
12	–1.3	–0.9	Удовл.
13	0.4	0.1	Удовл.
14	0.8	1.5	Удовл.

для оценивания результатов МСИ был выбран z-индекс z = ( X- xpt) / ^pt, (11)

где: x i — результат измерений лаборатории, %; x pt — приписанное значение, %; σ pt — стандартное отклонение для оценки квалификации, рассчитанное в соответствии с ГОСТ Р 50779.60-2017 [9].

Качество результатов измерений показателей оценивалось в соответствии с ИСО/МЭК 17043:2010 [10] и ГОСТ Р 50779.60-2017 [9] путем сравнения значения z -индекса с установленным нормативом контроля:

• 1)    при | z | ≤ 2.0 — результаты измерений признают удовлетворительными и не требующими выполнения действий;

• 2)    при 2.0 < | z | < 3.0 — результаты измерений признают сомнительными и требующими выполнения предупреждающих действий (сигнал предупреждения);

• 3)    при | z | ≥ 3.0 — результат измерений признают неудовлетворительным (неприемлемым)

и требующим выполнения корректирующих действий (сигнал к действиям).

Таким образом, все участвующие лаборатории показали удовлетворительный результат как для твердой, так и для мягкой пшеницы.

ВЫВОДЫ

В ходе работы были получены следующие результаты.

• 1.    Подобрана математическая модель, описывающая прохождение света в зерне.

• 2.    Дано определение показателя стекловидно-сти как характеристики рассеяния света в зерне и приведен способ определения коэффициента рассеяния.

• 3.    Подобран спектральный состав излучения, наиболее подходящий для определения стекло-видности.

• 4.    На основе математического описания стек-ловидности был предложен и реализован способ согласования измерений стекловидности в разных

• 5.    Проведена апробация способа согласования измерений, который показал удовлетворительный результат, позволяющий рекомендовать его к использованию.

лабораториях с использованием оптического эталонного образца.