Определение аффинной структуры объекта по движению

В контексте задачи стереозрения технических систем камеры, используемые для получения входных изображений, обычно калибруются так, что их внутренние пара

уравнения проекции

метры известны, а внешние параметры определены относительно некоторой глобальной системы отсчета. Такое

' м ¹

V 7

= — к z_r

' 0

V

z

' r 7

(Q 1 1( ^р 1 Г T 1 I 1 I ,

V А 7

допущение значительно упрощает процесс восстановления трехмерной формы объекта. Однако с точки зрения практической значимости более интересным случаем является ситуация, когда положения видеокамер и, возможно, их внутренние параметры не известны априори и могут меняться со временем. Такое положение является обычным для приложений визуализации на основе анализа изображений, когда видеоклип, записанный посредством ручной камеры с изменением масштаба в процессе съемки, используется для фиксации формы объекта и его визуализации при новых условиях наблюдения. Аналогичная задача возникает и в системах активного зрения, калибровочные параметры которых динамически варьируются (например, при навигации адаптивных мобильных роботов, изменении параметров вследствие большого ускорения при взлете и посадке автоматических планетарных зондов).

Рассмотрим геометрическую задачу оценки трехмерных положений соответствующих точек объекта в некоторой глобальной системе отсчета на основе использования согласованных элементов изображений, т. е. вос

где Р - неоднородный координатный вектор точки Р во внешней системе отсчета; О - вектор системы координат Отметим, что величина z , постоянна и поэтому можно записать

к =

^Ь 2 ^р 0 |           def

„ т 1 , ^{где к} 2 =

V 7

' а

V

^^^^^^

^а ctg е 1

sin е

def ( u 0 и р 0 = I

I ^v 0

.

Это позволяет переписать уравнение в виде ( Р 1

р = м I 1 ,

становления структуры сцены, и проекционных матриц, соотнесенных с камерами наблюдения (что эквивалентно движению точек относительно камер). Допустим, что рассматриваются сцены, рельеф которых изменяется незначительно по сравнению с их общей глубиной относительно камер, наблюдающих эти сцены, так что перспективу можно аппроксимировать простыми аффинными моделями процесса формирования изображения.

Выведем уравнение слабоперспективной проекции. Если через z обозначить глубину контрольной точки R , то два этапа проектирования Р ^Р'^р можно записать

где М - проекционная матрица размером 2x4, М = (A b); р = (и, v)Т - неоднородный координатный вектор точки г. В этом выражении матрица А размера 2 x 3 и двухзначный вектор b задаются соответственно формулами А = — К2Q2 и Ь = — К212 + р0, где Q -матрица zr zr размером 2x3, образованная двумя первыми строками матрицы Q; t2 - двухзначный вектор, образованный двумя первыми координатами вектора t. Отметим, что значения z,, а и в в выражении для М объединены и значение z , как правило, заранее не известно, поэтому можно записать:

м =±⁽ k* К ₁ 2 ) , (2) z r V 0 1 7

где k и s - соответственно формат изображения и наклон камеры. В частности, матрица слабоперспективной проекции задается двумя внутренними параметрами ( к и s ), пятью внешними параметрами (три угла, определяющие Q ₂ , и две координаты 1 ₂ ) и одним структурным парамет

в нормированной системе координат, привязанной к камере, следующим образом

ром, зависящим от сцены, а именно: z , .

Можно показать, что уравнение параперспективной проекции записывается в общей аффинной форме (уравнение (1)) с параметром М , равным

(X 1

( X 1

^{м 1 (} x/z,

y ^ y ^ v = y/z,

■ r ¹

Г r ,

М = — zr

ks

( 1 ⁰

I

0 1

Vv

- x_r / z r - y r / z r

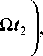
z

V 7

V zr7

или в матричной форме

V

V 1 7

/ — \

u

—

1 V7

zr

0 V

( X 1

z r 7

^y z 1

где переменные x ,y и z - это координаты контрольной точки R в нормированной системе координат камеры. Заметим, что выражение (3) сводится к уравнению слабоперспективной проекции (2) при условии х , = у , = 0. Согласно уравнению (3), матрица параперспективной

Если ввести калибровочную матрицу камеры К и ее внешние параметры Q и t , то можно получить общий вид

проекции задается двумя внутренними параметрами ( k , s ), пятью внешними параметрами (три угла, определяющие Q, и две координаты 1 ₂ ) и тремя структурными параметрами х , , у , и z , .

На практике в качестве контрольной точки часто берется характерная точка объекта, проекцию которой легко наблюдать на изображении. При этом координаты х_г , у_г и z этой точки измерить на изображении нельзя, но можно определить координаты ее проекции м и г . Перепишем уравнение (3) в следующем виде:

М = — zr

( k s u _n - u_r i (k

I 0 r ° I

V 0 1 v 0 - v r J     ( 0

5 I

1 1 *²

.

При такой формулировке матрица параперспектив-ной проекции задается четырьмя параметрами ( k , s , м ₀ и v ₀ ), пятью внешними параметрами (три угла, определяющие Q, и две координаты t ₂ ) и единственным структур

ным параметром z_r .

Уравнения ортогональной и параперспективной про

екций получаются по уравнениям слабоперспективной и параперспективной проекций, если положить значение

переменной z равным некоторой фиксированной величине (на практике часто берут z_r = 1) и подставить результат в выражения (2), (3) или (4). Если одна сцена наблюда

ется с помощью нескольких ортогональных камер (что соответствует последовательности изображений, снима

емых с помощью одной камеры с переменным фокусным расстоянием), то становятся важными реальные ко

эффициенты увеличения изображения, а упрощенные

калибровочные матрицы, которые фигурируют в уравнениях (2), (3) или (4), следует заменить матрицей ° ₂ .

Таким образом, при и фиксированных точках Р (j=1, ..., и ), которые наблюдаются т аффинными камерами, и соответствующих ти векторах (в неоднородных коорди

натах) р „ этих изображений аффинные проекции из формулы (1) можно переписать таким образом:

Р у = ^М,

( P V

= Ар j + b i для i = 1

., т и / =1, ..., и . (5)

Следовательно, определение аффинной группы по

движению - это задача оценки т матриц М . = ( А . b . ) размера 2 х 4 и и положений R точек Р в некоторой глобальной системе координат ти соответствиям элементов изоб

ражения р

Если проекционные матрицы М . могут иметь любой вид, когда (неизвестны внутренние и внешние параметры камер), по формуле (5) получаем 2 ти условий на 8 т + 3 и неизвестных коэффициентов, по которым определяются матрицы М . и положения точек Р . . Поскольку для достаточно больших значений т и и число 2 ти значительно больше суммы 8 т + 3 и , то очевидно, что большое число точек наблюдения и достаточно большое число точек объекта позволяют восстановить соответствующую струк

туру и параметры движения, например посредством схем наименьших квадратов. Здесь важным моментом являет

ся то, что если матрицы М. и Р . - это решения уравнения (5), то решениями также являются такие матрицы М . и

Р', что М ’ = М. Т и j ^{,                     1              1}

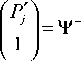
( Р , )

, где Т - матрица

V ¹ J

произвольного аффинного преобразования. Иными сло

вами, матрицу Т можно записать следующим образом:

Т =

( с

O T

d

и Т ^{- 1}

V

( C ^{- 1}

O

T

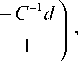
где С - несингулярная матрица 3 х 3; d - вектор в пространстве R ³ . Таким образом, любое решение задачи нахождения аффинной структуры по движению можно определить только с точностью до аффинного преобразования. Учитывая, что общее аффинное преобразование задается 12 параметрами, следует ожидать, что число возможных решений будет конечным, так как 2 ти >8 т + +3 и - 12. При т = 2 для определения (с точностью до аффинного преобразования) двух проекционных матриц и положения в трехмерном пространстве любой точки должно быть достаточно четырех точечных соответствий.

Если внутренние параметры камер известны (в этом случае калибровочные матрицы можно считать единичными), то на параметры проекционных матриц М = ( А. b) нужно наложить дополнительные условия. Например, матрица А . , соотнесенная с откалиброванной слабоперспективной камерой, формируется из первых двух строк матрицы поворота, умноженных на обратную глубину соответствующей наблюдаемой точки. Подобные ограничения могут использоваться для устранения аффинной неоднозначности при наличии достаточного числа изображений. Таким образом, решение поставленной задачи разбивается на два этапа [1]:

• -    использование по крайней мере двух изображений сцены для создания однозначного (с точностью до произвольного аффинного преобразования) трехмерного представления сцены, называемого ее аффинной формой. При этом аффинная форма наблюдаемой сцены восстанавливается по характерным точкам, согласованным для последовательности изображений;

• -    применение дополнительных точек наблюдения сцены и условий, связанных с известными калибровочными параметрами камер и конкретными аффинными моделями, для однозначного определения жесткой евклидовой структуры сцены.

На первом этапе получается необходимая часть решения, поскольку аффинная форма - это завершенное трехмерное представление сцены, которое можно использовать для синтеза новых проекций сцены. На втором этапе определяется Евклидово уточнение сцены, т. е. определяется аффинное преобразование, отвечающее жесткой структуре сцены и отображающее ее аффинную форму в Евклидову форму представления. При этом если использовать три и большее число изображений, то задача определения структуры по движению получается переопределенной (по схеме наименьших квадратов можно получить более устойчивое решение).

Рассмотрим определение аффинной структуры и движения по двум изображениям одной сцены. Известны две взаимодополняющие технологии определения структуры по движению: геометрическое восстановление сцены с целью выявления ее аффинной формы, по которой можно определить проекционные матрицы, и нахождение проекционных матриц с помощью геометрических манипуляций, что позволяет вычислить положение точек наблюдаемого объекта.

При геометрическом восстановлении сцены считается, что двух аффинных проекций четырех точек А , В , С , D должно быть достаточно для вычисления аффинных координат любой другой точки Р в базисе ( А , В , С , D ). При

этом предполагается, что аффинная проекция плоскости на другую плоскость представляет собой аффинное преобразование. В частности, если точка Р принадлежит плоскости П, которая содержит треугольник АВС , то ее аффинные координаты в базисе П, сформированном тремя

этими точками, можно непосредственно измерить на любом из двух изображения. В работе [2] сформулирована и доказана теорема об определении аффинной структуры по движению: для двух заданных аффинных проекций четырех некомпланарных точек аффинная форма сцены определяется однозначно.

При алгебраической оценке движения пренебрегают геометрической природой объекта и производят простые алгебраические действия по упрощению вида проекционных матриц [1], в результате чего получают простой метод восстановления таких матриц и соответствующей аффинной формы объекта. Введем аффинный эквивалент эпиполярного условия. Рассмотрим два аффинных изображения и перепишем соответствующие проекци

Отметим, что первых трех уравнений системы (6), в принципе, достаточно для нахождения P как ( и , v , и’ ^Т , без определения коэффициентов а, Ъ , с и d и наличия минимального числа соответствий. Но использование всех четырех уравнений может дать более точные результаты.

Теперь рассмотрим задачу восстановления структуры аффинной сцены и соответствующих проекционных матриц при наличии потенциально большого набора изображений. Будем считать, что статичная сцена наблюдается с помощью фиксированного набора т аффинных камер. Через р_р ...,р _т будем обозначать т проекций точки сцены Р . Уравнение (5) в этом случае можно переписать следующим образом:

q = r + АР ,

онные уравнения:

Гр = АР + b , 1             ^п р ^и

[р = АР + b

( А р - b '( Р

А р - b - 1

V р А

= 0 .

Необходимым и достаточным условием наличия не

тривиального решения данных уравнений будет равен

ство детерминанта нулю

Det

, Р,   .1= 0 , или а и + В v + а' и + В' v' + 5 = 0 ,

А р - b

V р /

где а, в, а ', [' и 8 - константы, зависящие от А , b ,А и b '; uOv и и 'O'v'- системы координат первого и второго изоб-

ражений соответственно. Такое условие называется аффинным эпиполярным условием.

Вообще говоря, аффинную эпиполярную геометрию можно рассматривать как предельный случай перспек

тивной геометрии. Действительно, можно показать, что аффинное изображение является пределом последовательности изображений, полученных перспективной камерой, увеличивающей масштаб изображения сцены при одновременном удалении от нее. Данное эпиполярное условие можно записать следующим образом:

( 10 0 и A

Det

v

и

= - au - bu - cu + v' - d = 0 .

a b c v - d

^V                /

Здесь коэффициенты а,Ъ , с и d связаны с параметра

ми а, [, а', [' и 8 соотношениями а :а = Ъ :[ = с :а' = =-1: [' = d : 8. При наличии достаточного числа точечных

соответствий коэффициенты а ,Ъ ,сиd можно оценить по схеме наименьших квадратов. В данном случае две про

екционные матрицы становятся известными и положение любой точки можно оценить по координатам ее изображений. При этом решается соответствующая система

из четырех уравнений с тремя неизвестными координатами р :

( 10 0 и A

a

V

0 b

c

v u '1

v ' - d

/

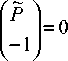
def где q =

⁽ P i '

;

V pm7

def f ^ ' r = ...

;

def

А =

^A i

.

b

^V m 7

A

^VA m J

Если через I обозначить множество всех изображе-

ний т камер, то получим

I = { r + АР | Р е R 3 } = r + V A , где V - диапазон возможных значений матрицы А размера 2 т х 3. Другими словами, множество I - это трехмерное подпространство аффинного пространства R ^{2 т} .

Предположим, что началом системы координат объекта является одна из наблюдаемых точек или центр масс, например Р ₀ , куда можно перенести начало системы координат изображения р ₀ . Преобразование р ^ р - р ₀ фиксирует начало координат набора изображений I , которое теперь становится трехмерным векторным пространством Б Д . Иными словами, для любой точки Р и для 1 = 1,..., т можно записать, чтор= АР . Эквивалентно, q =АРи

I = { АР | Р е R 3 } = V A .

В общем случае ранг произведения матрицы D размером 2 т х 3 и матрицы размером 3 х п равен 3. Если принять, что UWV ^T - это разложение по сингулярным значениям (так называемое SVD -представление) этой матрицы, то тогда только три сингулярных значения являются ненулевыми. Следовательно, D = U _; W _; V _; ^Т , где U _; и V _; - матрицы 2 т х 3 и 3 х п , сформированные тремя левыми крайними столбцами матриц U и V ; W _; -диагональная матрица 3 х 3, сформированная соответствующими ненулевыми сингулярными значениями.

В качестве представления истинного (аффинного) движения камеры и формы сцены можно взять матрицы А ₀ = U _; и Р ₀ = W _; V _; ^Т . Действительно, столбцы матрицы А , по определению, формируют базис диапазона значений VA матрицы D , тогда как столбцы матрицы А ₀ , по построению, формируют другой базис этого векторного пространства. Отсюда следует существование такой матрицы Т размером 3 х 3, что А = А ₀ Т и, следовательно, Р = Т ¹ Р ₀ . И наоборот, D = ( А ₀ Т)(Т ¹ Р ₀ ) для любой обратимой матрицы Т размером 3 х 3. Если же помимо этой линейной неоднозначности учесть степени свободы, соответствующие возможности выбора положения начала

координат глобальной системы отсчета, то получим еще одно подтверждение аффинной неоднозначности задачи определения структуры по движению. При этом разложение по сингулярным значениям позволяет получить репрезентативные оценки аффинного движения и структуры сцены.

Отметим, что приведенные выше рассуждения справедливы только для идеализированной ситуации отсутствия помех. На практике обычно присутствует так называемый шум изображения, который приводит к ошибкам при локализации характерных элементов изображения. Наличие такого шума объясняется тем, что реальные камеры не являются аффинными, уравнение D =АР не выполняется строго, а матрица D имеет (в общем случае) полный ранг

Рассмотрим процесс преобразования аффинных изображений в Евклидовы. Предположим, что жесткий объект наблюдается двумя ортографическими откалиброванными камерами, а точки изображения представляются их нормированными координатными векторами. В этом случае преобразование между координатными системами можно записать как суперпозицию вращения и трансляции (под трансляцией будем понимать такое положение двух систем координат, когда их базисные векторы параллельны, но начала координат находятся на некотором расстоянии друг от друга).

При ортографической проекции трансляция по глубине не имеет видимого результата, а трансляция в плоскости изображения (фронтально-параллельное трансляция) легко устраняется выравниванием двух проекций некоторой точки объекта А . Любое вращение вокруг направления наблюдения также легко определяется и устраняется: две точки наблюдения связаны вращением вокруг оси во фронтально-параллельной плоскости, которая проходит через проекцию точки А . В работе [2] показано, что существует однопараметрическое семейство таких вращений, которое определяет форму с точностью до изменения масштаба по глубине и сдвига, и что добавление третьей точки наблюдения окончательно ограничивает решение одной или двумя парами точек, связанными через отражение во фронтально-параллельной плоскости.

Существует простой метод перехода от аффинной структуры к Евклидовой при условии, что аффинные проекционные матрицы камер приблизительно известны. Рассмотрим ортографическую, слабоперспективную и параперспективную модели процесса формирования изображения в предположении, что камеры откалиброваны. При этом можно воспользоваться аффинными проекциями уравнения (5) с учетом определенных условий, наложенных на компоненты проекционной матри цы М = (A b). Напомним, что слабоперспективная проекционная матрица описывается уравнением (2). Если камера откалибрована, то можно использовать нормированные координаты изображения и допустить, что к=1 и s = 0. При этом проекционная матрица принимает вид

М = ( A b ) = -1 ( я ₂ t 2 ) .            (7)

zr

Ортографическая камера - это слабоперспективная камера с параметром zr = 1. По уравнению (7) следует, что матрица A является частью матрицы вращения, а еди-—    — ничные векторы-строки аг и a2 ортогональны между собой. Иными словами, ортографическая камера - это аффинная камера с дополнительными условиями — —         — 2    — 2

a i ■ a 2 = 0 и a i = a 2 1 = 1 .

Общий случай слабоперспективной камеры подобен рассмотренному, но при этом строки матрицы A уже не являются единичными векторами. Следовательно, слабоперспективную камеру можно рассматривать как аффин- — —         ^{— 2     — 2}

ную камеру с двумя условиями: a ■ a 2 = 0 и | a 1 = | a 2I .

Наконец, используя параметризацию параперспектив-ных камер, представленную в виде уравнения (4), легко показать, что параперспективная камера - это аффинная камера, удовлетворяющая следующим условиям:

— — u,v, a ■ a =---- r r,

^{1 2} 2(1 + u 2 )

I — |2        urvr a +

^{1 1} 2(1 + v 2 )

I a2\ ,

(1 + u 2 )

a'

(1 + v 2 ) ^,

где параметры u_r и v_r - координаты перспективной проекции опорной точки R , определенной в параперспек-тивной проекционной модели.

Таким образом, разделение задачи определения структуры по движению на аффинный и Евклидов этапы позволяет использовать простые и устойчивые методы восстановления формы объекта по последовательности его изображений. Аффинный этап описывает трехмерную сцену линейными уравнениями и представляет основу для определения сегментации сцены при анализе движения объекта. При этом траектории точек объекта на образах описываются линейными комбинациями траекторий его трех опорных точек. На втором этапе вводятся Евклидовы ограничения и уточнения структуры сцены на основе нескольких изображений.