Определение базисных контуров с помощью графа в электрических системах
Автор: Тиллабоев .к, Холмирзаев И.А.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Основной раздел
Статья в выпуске: 7 (13), 2016 года.
Бесплатный доступ
Определено базисных контуров с помощью элементов теории графов и алгебри матриц.
Электрические схемы, граф, дерево, хорды, матрица
Короткий адрес: https://sciup.org/140269572
IDR: 140269572
Текст научной статьи Определение базисных контуров с помощью графа в электрических системах
Известно, что, схемы замещения в современных сложных электрических систем содержат десятки и даже сотни узлов и ветвей. Естественно, что для таких систем количество уравнений состояния соответственно настолько велико, что для их решения необходимо использовать современные электронные вычислительные машины. Более того, составление уравнений состояния для сложных схем является весьма трудоемкой процедурой, и решение данной задачи также целесообразно возложитъ на компьютер. Для этого требуется иметъ формализованный подход к составлению уравнений, который был бы одинаков для схем любой сложности и конфигурации. Такой подход можетъ бытъ разработан на основе аналитического представления конфигурации схемы замещения с помощью элементов теории графов и алгебры матриц [1].
Для иллюстрации вышесказанного рассмотрим следующую электрическую схему:
D
рис.1
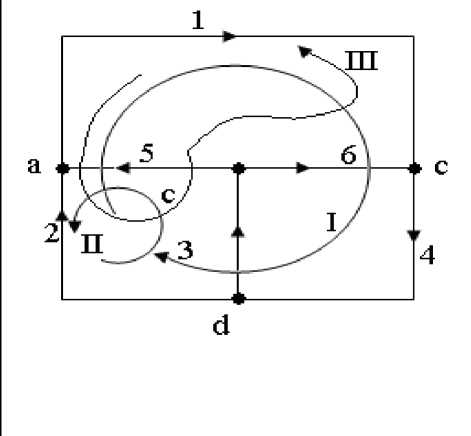
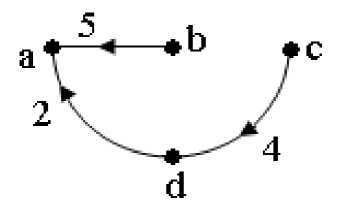
На рис 2. данная схема показана в виде связанного направленного графа на которой выбраны направления ветвей, а также указаны номера ветвей и узлов.
Рис.2
Для
направленного
графа, Выбрав узел d в качестве
показанного рис. 2, матрица M балансирующего, получим матрицу имет вид:
M из M путем исключения
Mz
последней строки:
|
"+1 |
- 1 |
0 |
|
|
M = |
0 |
0 |
- 1 |
|
-1 |
0 |
0 |
0 - 10
0 + 1 + 1
+ 1
- 1
По известной матрице M непосредственно определить матрицу N невозможно. Это связано с тем, что одной и той же электрической цепи в общем случае соответствует несколько различных систем независимых контуров, или, иными словами, одной и той же матрице M можно поставить в соответствие несколько матриц N.
Однозначность в выделении системы независимых контуров, позволяющая получить матрицу N по матрице M, может быть достигнута при использовании таких понятий теории графов, как дерево и хорды. Одна и та же схема может быть разделена на дерево и хорды по-разному.
Для простых схем, аналогичных рассмотренной, выделение ветвей дерева и хорд и даже всех возможных вариантов разделения графа на соответствующие подграфы не представляет труда. В результате матрице M, записанная первоначального при произвольной нумерации ветвей, путем перестановки столбцов преобразуется к виду
M = [ M j M e ]
где M - подматрица (блок), относящаяся к дереву схемы, M - подматрица, характеризующая подграф, состоящий из хорд.
Аналогично можно разделить на блоки и матрицу N
N = [ N a N , ], где N a =- M J ' ( M j ) - ' ; N , = 1
Матрицу Np можно задать равной единичной матрице ( Np = 1 ). Это соответствует выбору системы таких контуров, которые характеризуется следующими свойствами:
-
• каждый из контуров замыкается одной хордой т.е. каждая хорда входит только в один контур;
-
• последовательности нумерации хорд и контуров одинаковы;
-
• направления обхода контуров и замыкающых их хорд совпадают. Рассмотренные контуры называются базисными.
Для определение базисных контуров рассмотрим слудующие два варианта дерево и хорды. (Вообщем их число много). Вариант 1.
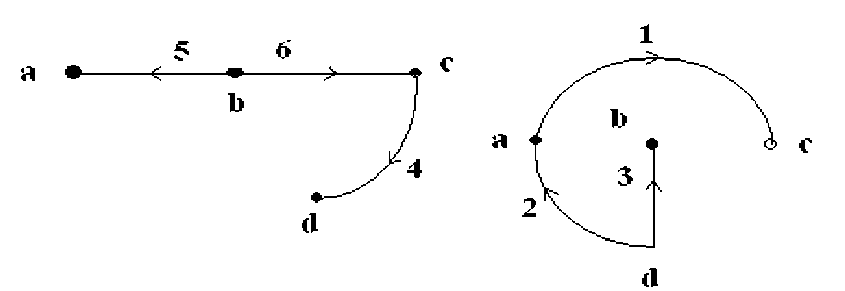
хорды дерево
Операции над матрицами возложили на МathCAD.
( 1 10 10 0 A
|
N = |
0 |
- 1 |
1 |
0 |
10 |
|
I- 1 |
- 1 |
1 |
0 |
0 1 ) |
Матрице N – соответствует три
контура:
-
1) 1, 2, 4
-
2) 2, 3, 5
-
3) 1, 2, 3, 6
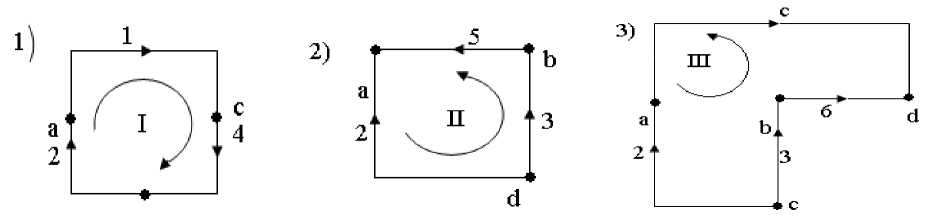
Видно, что в этом случае свойства базисных контуров выполняется.
-каждый из контуров замыкается одной хордой т.е. каждая хорда входит только в один контур (При этом хорда 4 входит только в первый контур, хорда 5 входит только в второй контур, хорда 6 входит только в третий контур);
-
-последовательности нумерации хорд и контуров одинаковы;
-
-направления обхода контуров и замыкающых их хорд совпадают.
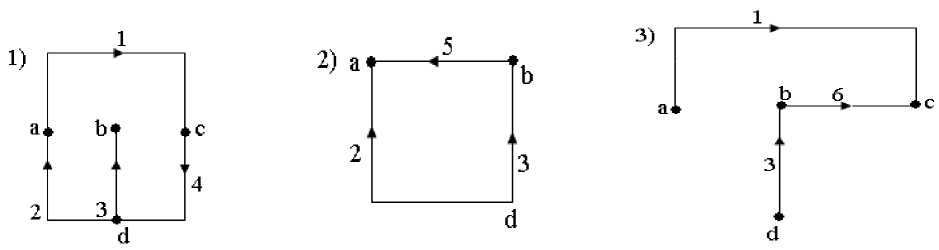
Вариант 2.
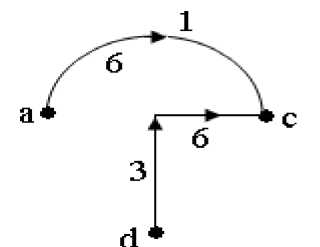
хорды
дерево
- 1
- 1
1 0 0 A
Матрице N – соответствует три контура:
1) 1, 2, 3, 4 2) 2, 3, 5 3) 1, 3, 6
N = 01 1010
v 1 0 - 10 0 1 v
Видно, что в этом случае свойства базисных контуров невыполняется.
В заключение можно сказать, что выбрав любой вариант дерево и хорды мы не получим правильный ответь. При выборе базисных контуров проверили многие варианти, а здесь для простати провели два примера.
Список литературы Определение базисных контуров с помощью графа в электрических системах
- В.А.Веников и др. Математические задачи электроэнергетики. М., В.школа, 1987г


