Определение целевой конфигурации мобильного манипулятора в задачах схвата объектов

Мобильный манипулятор (ММ) - это робототехническая система, представляющая собой колесную или иную подвижную платформу, с закрепленным на ней робототехническим манипулятором. Платформа обеспечивает перемещение системы в среде, а манипулятор -ее взаимодействие с окружением, что расширяет область применимости таких систем [1-4]. ММ могут применяться для решения различных робототехнических задач, в том числе в человекоориентированных средах, т.е. таких, которые изначально предназначены для работы людей, а не роботов. Примерами таких сред являются жилые, офисные, медицинские, торговые и другие подобные помещения. В качестве подвижной платформы ММ могут использовать различные мобильные устройства, такие как БПЛА [2,3] или шагоходы [1], однако в данной работе мы рассматриваем распространенный вариант, когда в качестве мобильной базы используется колесная платформа. ММ с такой платформой обычно имеет девять степеней свободы и выше (мобильная платформа - три степени, манипулятор -от шести) и является кинематически избыточной робототехнической системой. Для такой системы требуется совместное целеполагание с учетом ограничений базы и манипулятора. Неполная наблюдаемость среды создает трудности для выполнения задач ММ, а ограниченная маневренность колесных платформ замедляет выполнение задач. Если роботу требуется захватить объект, то для оценки позы схвата требуется уже подъехать к цели и, вероятно, может потребоваться перепарковка. Поэтому важно по неполным данным определить некоторую цель для планирования, из которой робот сможет захватить объект с высоким шансом на успех.

В данной работе предлагается подход к определению целевой конфигурации мобильного манипулятора для заданного положения захвата. Предлагаемый подход основан на свертках карты занятости, получаемой с LiDAR набором ядер. В качестве ядер свертки используются проекции формы робота (т.н. футпринт) на плоскость карты под различными углами, что позволяет определить конечное множество безопасных положений платформы. Область достижимости манипулятора аналогичным образом проецируется на карту занятости и используется в качестве ядра свертки, что позволяет оценить конечное множество положений платформы, из которых манипулятор может захватить объект.

Разработанный метод был протестирован в симуляторе Nvidia Isaac Sim1 на специально разработанных средах (см. раздел 4) и показал эффективность в сравнении с подходами, используемыми в литературе.

1.1.    Обзор литературы

Обычно задача определения конфигурации для захвата объектов рассматривается для статичных манипуляторов. Примером такого подхода является работа [5]. CAD-модель объекта, который необходимо захватить, оптимизируется относительно облака точек, отображающего объект. Затем компонент планирования вычисляет траекторию для манипулятора, позволяющую захватить объект. Этот подход исходит из предположения о закрытом мире: для каждого объекта, который необходимо захватить, существует точная CAD-модель. В литературе известны подходы, напрямую использующие облака точек без их классификации, что позволяет обходиться без SD-моделей объектов [6, 7]. Обе указанные работы базируются на фильтрации сгенерированных кандидатов точек схвата с помощью CNN. Для автономного робота, чьи вычислительные ресурсы ограничены, такая фильтрация может оказаться вычислительно трудной. Помимо детекции захвата на роботе в реальном времени должны работать подсистемы локализации, сегментации и трекинга объектов. Авторы [7] учли времязатратность выполняемых по отдельности операций сегментации, а затем детекции захвата, и объединили их в одной нейросетевой архитектуре.

Вышеуказанные работы реализуют планирование схвата объекта стационарным манипулятором без мобильной платформы. Для ММ требуется дополнительно генерацию це- лей для платформы поставить в зависимость от возможностей манипулятора. Наиболее близка к такому коллаборативному выполнению задач манипулятора и платформы работа [8]. Данная статья представляет реализацию замкнутого цикла динамического отслеживания и захвата объекта с предварительным знанием целевой позы. В реальных случаях целевая поза заранее неизвестна, а оценить позу робот сможет только доехав до объекта. Перепарковка робота после оценки позы займет некоторое время, что неэффективно. В статье [9] ставится оптимизационная задача совместного движения рабочего органа ММ по ключевым точкам. Приоритет отдается минимизации перемещений платформы, но разница между конфигурациями манипулятора для передвижения между точками также включена в функцию стоимости. Авторы демонстрируют этот подход на искусственном примере, без практического приложения. Решение может быть полезным, когда ММ требуется произвести серию действий в близко расположенных точках пространства. Проблема поставлена так, что конфигурации рабочего органа заранее известны и точны, т.е. отсутствует элемент неопределенности среды. В реальных условиях ММ нужно решать задачи, когда финальная целевая конфигурация не известна до выполнения части плана: ММ может находиться в одной комнате, а целевой объект в другой.

1.2.    Вклад

В этой работе предложен и реализован подход к осуществлению схвата объектов мобильным манипулятором. Подход учитывает препятствия вокруг целевого объекта путем выполнения сверток футпринта с картой занятости и учетом области достижимости манипулятора. Это позволяет сгенерировать задание на планирование траектории мобильной платформы в условиях неопределенности целевой конфигурации рабочего органа манипулятора. Разработанный метод может быть адаптирован для другой конфигурации манипулятора и платформы.

2.    Постановка задачи

Эта работа сосредоточена на выделении целей для планировщиков платформы и манипулятора при решении задач схвата объектов в помещениях. Объекты находятся на открытых поверхностях (пол, стул, стол и т.д.). ММ должен подъехать к целевому объекту и захватить его рабочим органом.

В качестве модельной робототехнической системы рассматривается мобильный манипулятор, который состоит из 4-ко.лесной платформы Clearpath Husky2 с дифференциальным приводом и шестистепенного манипулятора UR53, как на рис. 1. На рабочем органе манипулятора установлен двупалый захват Robotiq4. На манипуляторе закреплено несколько камер глубины (Intel Realsense5 и Zed Camera6) и Velodyne LiDAR7. Intel Realsense установлен на рабочем органе манипулятора, именно эта камера используется для точного позиционирования объектов.

До того как платформа приблизится к целевому объекту, поза для захвата не известна. Ограничением является область достижимости точек манипулятором, которая меняется в зависимости от ориентации. Самым худшим случаем является ориентация захвата, перпендикулярная к поверхности, на которой лежит объект. Такая поза сильно уменьшает область достижимости манипулятора. Для платформы требуется определить точку с данными свойствами:

• •    В нее существует путь.

• •    Из нее возможно построить траекторию для манипулятора в координаты объекта с худшей ориентацией.

Рис. 1. Мобильный манипулятор husky

Для манипулятора требуется по облаку точек целевого объекта определить конфигурацию манипулятора, позволяющую захватить объект.

Конфигурация мобильного манипулятора S включает в себя положение мобильной базы Х ъ (декартовы координаты и ориентация) и конфигурацию звеньев манипулятора 0 (углы поворота каждого звена). Известна функция прямой кинематики мобильного манипулятора, позволяющая рассчитать положение и ориентацию гриппера Х _д = Х ъ + FK ( 0 ). Отметим, что нам также известен алгоритм расчета обратной кинематики, позволяющий рассчитать конфигурацию звеньев для заданной пары положения платформы и положения гриппера 0 = IK( Х _д - Х _ь ).

Входными данными для задачи являются: начальная конфигурация ММ S (0), множество точек целевого объекта Т, множество препятствий О. С учетом того, что движение мобильной базы и манипулятора планируется и выполняется по отдельности, задача планирования захвата разбивается на ряд подзадач:

• 1)    Определить целевое положение гриппера Х_д(Т) для захвата объекта;

• 2)    Определить целевое положение платформы ХДТ), которое не будет содержать коллизий с препятствиями и из которого будет достижимо Хд(Т);

• 3)    Определить план движения платформы из Хь(0) в ХДТ);

• 4)    Определить план движения манипулятора из конфигурации 0(0) в конфигурацию 0(Т).такунэ.чтоХд (Т )= Х_Ь(Т)+ FK (0(Т)).

3.    Метод

Подзадача 1 решается разработанным подходом на основе анализа облаков точек. Для решения подзадачи 4 применяется набор простых эвристик - эксперименты показали, что они являются достаточными для успешного планирования движения манипулятора. Для решения подзадачи 3 применяется классический алгоритм планирования А* [10], показавший свою эффективность при планировании на Occupancy Grid. Интерес представляют прежде всего новые подходы к подзадачам 2 и 3.

Определим конечную цель как д = [g_sp д_др], где g_sp = (х,у,0) - поза платформы, а 9 др = (^х, 9, z, а, /В, у ) - поза схвата. Таким образом задача поиска д разбивается на 2 подзадачи. Конечная поза схвата заранее неизвестна, поэтому для определения g_sp положим, что д др = (x,y,z, 0,^, 0).

occupancy grid

О 25      50      75     100     125     150     175

Рис. 2. Двухмерная карта занятости. Каждая клетка матрицы заполнена значениями: 0 - свободное место, 1 - препятствие

0.0    2.5    5.0    7.5    10.0 12.5   15.0   17.5

0.0    2.5    5.0    7.5    10.0 12.5   15.0   17.5

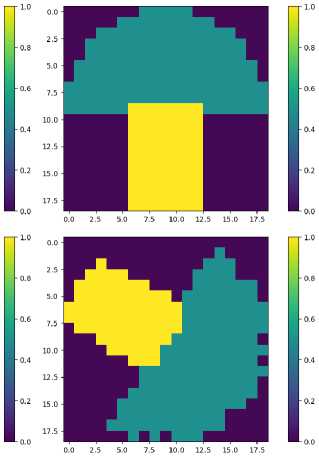
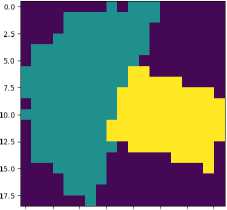
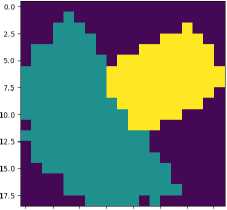
Рис. 3. Футприпт робота с различными углами поворота и разрешением, равным разрешению карты занятости. Прямоугольная область соответствует футпринту мобильной платформы, полукруглая - зоне достижимости манипулятора

3.1.    Выбор целевой позиции мобильной платформы

Введем следующие обозначения:

0 обозначает 2В-свертку с ЗО-ядром. Пусть A — т х п 2П-матрица, a B a х b х к ЗП-яяро. C = A 0 B • что (т — a) х (п — b) х к ЗП-тешор. Каждый (т — a) х (п — b) слой C является результатом свертки A с соответствующим слоем B

Пусть M og ~ двумерная сетка занятости (рис. 2), a Gf_p — трёхмерное ядро свертки, представляющее изображения клеток, занимаемых роботом (футпринт) для различных ориентаций (центр G f _p соответствует центру системы координат основания робота, рис. 3). Здесь и п — количество ячеек занятости, которое должно содержать максимальный размер футпринта робота; т — разрешение для дискретизации возможных ориентаций робота. Определим тензор безопасных поз T_sp как результат с вертки (рис. 4) M og ^и G fp-

T sp = M OG ⁰ G fp .

Пусть M^ — матрица положения цели (она имеет те же размеры, что и сетка занятости, ячейка, соответствующая целевому положению захвата, имеет значение 1, остальные ячейки имеют нулевое значение) и Gws — трёхмерное ядро свертки, представляющее рабочее пространство манипулятора для различных ориентаций (центр Gws соответствует центру системы координат следа основания робота). Рабочее пространство манипулятора зависит от высоты, на которой находится целевой объект, выбирается необходимый срез области достижимости манипулятора. Определим тензор достижимости цели Tgr как резулвтат свертки M^ 11 GwS:

T _9r = M _d 0 G _ws.

Зададим a_sp и a g _r как пороги для элементов из T _sp и Т ^у соответственно. Случайно семплируя точки в радиусе R от целевого объекта, найдем такие, что T _sp(0, х, у) <  a_sp и T gr ⁽^^,Х,у) ^ ^ gr-

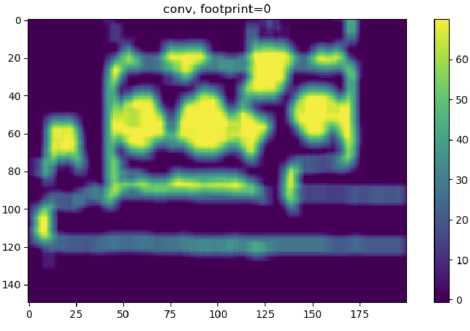
Рис. 4. Визуализация одного капала результата свертки футприита и карты занятости. Каждая клетка содержит значение, равное количеству пикселей с препятствиями, которые задевает робот в данных координатах

3.2.    Определение позы схвата

Поза схвата задается относительно системы координат объекта. Из облака точек нужно получить некоторую относительно предсказуемую систему координат. Наш метод основывается на поиске главной диагонали, это относится к анализу главных компонент (РСА) и часто связано с понятием последней главной компоненты. В контексте РСА главные компоненты вычисляются таким образом, что первая главная компонента объясняет наибольшую часть дисперсии данных, вторая главная компонента объясняет наибольшую возможную дисперсию среди оставшихся и так далее. Последняя главная компонента будет направлением, вдоль которого дисперсия минимальна.

Пусть имеется облако точек объекта O_t, которое представляет собой N точек в трехмерном пространстве. Для поиска главной диагонали используется линейная регрессия с L2 регуляризацией:

min(||Xw - У||2 + а||ш||2) W

В качестве матрицы наблюдений X возьмем x компоненты из O_t, обозначим ОД а целевая переменная у = О^. Полученная функция у*(х) = хш будет задавать главную диагональ, а коэффициенты х задают нормаль к разделяющей плоскости. Оставшийся вектор базиса целевого объекта можно найти векторным умножением (рис. 5).

Относительно полученного базиса задана матрица, которая совмещает главную диагональ объекта ( у ось) с у осью манипулятора и z ось объекта с z осью захвата. Точка схвата определяется как центр облака точек. Пример работы такого подхода показан на рис. 7.

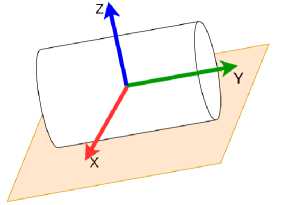
Рис. 5. Схематичное представление базиса объекта, полученного из облака точек с помощью ли нейной регрессии

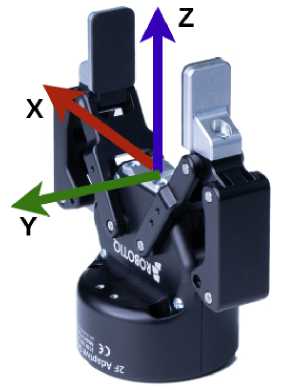
Рис. 6. Визуализация базиса захвата

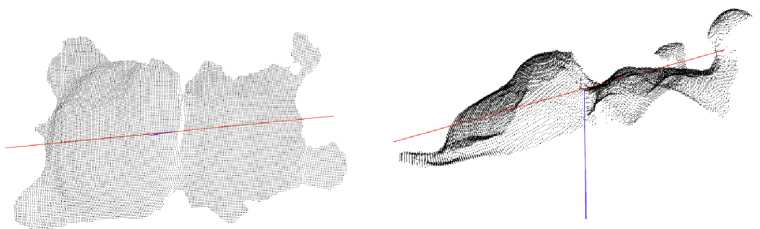
Рис. 7. Визуализация результата работы алгоритма построения базиса объекта. Наклонная линия - главная диагональ, вертикальная - нормаль разделяющей плоскости

4.    Эксперименты

Эксперименты проводятся в симуляторе Nvidia Isaac-Sim. Для оценки качества была создана среда, состоящая из двух столов, стен и целевого объекта (рис. 8). На каждом эксперименте начальная позиция робота задается случайным образом в пределах одной комнаты. После прогона алгоритма робот перемещается в полученную точку и запускается алгоритм захвата объекта. Для планирования трактории манипулятора используются встроенные методы API манипулятора. Управление происходит по точкам в декартовой системе координат. Успешным считается эксперимент, в котором произошла коллизия захвата манипулятора с целевым объектом.

Мы использовали в экспериментах три сценария:

• 1)    Два стола стоят перпендикулярно, объект создается рядом с пересечением (рис. 9).

• 2)    Два стола стоят параллельно, объект создается на столе (рис. 9).

• 3)    Аналогичен предыдущему, но между столами стоит стул, объект создается на стуле.

Рис. 8. Экспериментальная среда

Рис. 9. Сценарий №1 - слева, сценарий №2 - справа

Для демонстрации эффективности нашего подхода мы использовали три бейзлайна:

• 1)    Simple: Проводит вектор из текущей позиции робота до целевого объекта и отступает некоторый радиус от цели, эту точку и возвращает.

• 2)    А*: Карта занятости маскируется вокруг целевого объекта и планировщик строит до него путь с помощью классического алгоритма А* [10]. Далее узлы из конца пути отбрасываются так, чтобы конечная точка была на некотором радиусе от объекта.

• 3)    А*ф: Аналогичен предыдущему, но учитывает занятость соседних узлов при выборе нового.

Гиперпараметры алгоритмов с описанием и используемыми в экспериментах значениями представлены в табл. 1, а результаты приведены в табл. 2.

Ошибки обусловлены невозможностью найти точку за отведенное число итераций, подходящую по параметрам. Это происходит из-за низкого разрешения карты занятости и необходимостью использовать аналогичное разрешения футпринта и области достижимости. Разрешение было взято с реального робота, на практике у нас используется разрешение в 10 см на пиксель.

С учетом этих нюансов эксперименты показывают превосходство разработанного алгоритма над альтернативными простыми вариантами реализации, получая высокий процент успеха в различных конфигурациях среды.

Таблица 1

Гиперпараметры алгоритмов

Алгоритм	Гиперпараметр	Значение	Описание
Simple	R	0.8	Радиус отступа от целевого объекта
А*	R	0.7	От построенного пути узлы отбрасываются до тех пор, пока расстояние до объекта не будет больше или равно R.
	R t	2	Препятствия вокруг цели в пределах этого радиуса помечаются как свободные клетки для существования пути в точку.
А*+ FpConv	R	0.7	От построенного пути узлы отбрасываются до тех пор, пока расстояние до объекта не будет больше или равно R.
	R t	2	Препятствия вокруг цели в пределах этого радиуса помечаются как свободные клетки для существования пути в точку.
	R aware	2	Область проверки соседей па наличие препятствий
	R	1.3	Радиус поиска оптимальной точки
	I	2000	Количество итераций семплировапия
	R t	1	Радиус раздутия объекта
	& sp	0	Количество допустимых коллизий футпринта робота с препятствиями
	^ gr	0.55	Порог для достижимости в относительных величинах

Таблица 2

Успешность алгоритмов на 100 экспериментах

	Сценарий №1	Сценарий №2	Сценарий №3
Alg	SR, %	SR, %	SR, %
Simple	8	36	10
А*	55	47	76
А*+	58	55	71
FpConv	84	68	96

5.    Заключение

В данном исследовании рассмотрена задача схвата объектов с помощью мобильного манипулятора. Основной целью было определение целевой конфигурации мобильного манипулятора для захвата целевого объекта, учитывая положение объекта и наличие препятствий. Важной подзадачей явилось определение положения мобильной платформы и конфигурации звеньев манипулятора. Для ее решения был предложен и реализован алгоритм, рассчитанный на работу в тесных средах с высокой плотностью препятствий. Алгоритм включает серию сверток карты препятствий с использованием ядер, учитывающих геометрическую форму колесной базы и рабочее пространство манипулятора. Это позволяет определить множество допустимых положений платформы, из которых манипулятор может успешно захватить объект. Результаты экспериментов в симуляционной среде Isaac Sim показали эффективность предложенного подхода для работы в условиях тесных сред. Разработанный алгоритм улучшает способность мобильных манипуляторов выполнять задачи по сбору и перемещению объектов в сложных и ограниченных пространствах.