Определение давления изделий из упругих трикотажных полотен на тело человека

Значительный удельный вес в объеме продукции швейной промышленности занимают плотно облегающие трикотажные изделия с эластомерными нитями в структуре. Особенностью таких нитей является наличие упругих деформаций, не пропорциональных силам, возникающим в процессе эксплуатации изделий, т.е. не подчиняющихся законам Гука.

Формообразование плотно облегающих трикотажных изделий производится способом поперечного заужения деталей относительно размеров тела человека в сочетании с направлением перекоса петельных рядов полотен. Известно, что зауженные изделия оказывают определенное давление на различные участки тела человека. Давление, оказываемое трикотажными изделиями как бытового, так и медицинского назначения на различные участки тела человека, нормировано за исключением области груди [1]. Однако для сохранения здоровья женщины, давление, оказываемое на эту область должно быть минимальным.

Логично предположить, что максимальная величина давления изделия приходится на область выступающих точек и будет зависеть от их формы, и как следствие, радиуса кривизны поверхности.

Для определения давления изделия на выступающую точку предположим, что на участке изделия АВ шириной L деформации растяжения вызваны силой F, которая создает давление на малую площадку шириной dS на поверхности тела в выступающей точке D. Т.к. величина dS мала, можно считать, что она расположена на аппроксимирующей параболе и на окружности, вписанной в эту параболу, с одним и тем же радиусом кривизны R.

Рисунок! - Способ определения кривизны поверхности

Давление на площадку dS можно определить по формуле [2]:

2 dF p =--- z , dS

где dFz - сила, действующая на края площадки параллельно оси симметрии рассматриваемого участка, вычисляется по формуле:

dF^ = F sin d а = F d а , (2) где d а - малый угол между осью симметрии и отрезком ОС , равным радиусу кривизны параболы аппроксимирующей форму поверхности тела.

dS = 2 LRda, (3), где L - ширина участка, равная ширине пробы полотна по методике, установ- ленной ГОСТ 8847-85[3]. Подставив выражения (2) и (3) в формулу(1), получим зависимость величины давления от радиуса кривизны поверхности:

F

p — —. RL

Из формулы (4) видно, что давление р прямо пропорционально приложенной силе и обратно пропорционально радиусу кривизны и ширине испытуемого участка трикотажного полотна.

Сила F может изменяться в пределах до 6Н согласно ГОСТ 8847-85 в зависимости от назначения изделия. Зная растяжимость ткани в поперечном направлении 5пп и ее относительную деформацию на выступающих частях тела ei можем получить формулу для определения давления в виде[4]:

p —--

RL при L и R – в метрах.

•

e i , Па, пп

Проблема вычисления давления связана с определением радиуса кривизны в верхней точке исследуемого объекта, где радиус будет наименьшим, давление примет наибольшее значение. Экспериментально проведены измерения груди в плоской ортогональной системе координат, в которой ось Ох направлена по линии груди, ось Oz - перпендикулярно поверхности тела. Такое расположение осей позволяет полученные измерения аппроксимировать параболой в канонической форме:

Z — — + Zo , 2 p

где 2 р - расстояние от вершины параболы до точки ее фокуса по оси симметрии.

Определение параметров аппроксимирующей параболы можно осуществить методом наименьших квадратов, т.е. оптимизации целевой функции, равной сумме квадратов невязок.

Обозначим P=2p , тогда уравнение параболы примет вид:

Z — — + Zo .            (7)

P

Составим целевую функцию, равную сумме квадратов разностей (квадратов невязок - см. рис.2) теорети- ческих и измеренных значений зависимых переменных Zi, соответствующих высоте точек на поверхности груди. На рис.2 график параболы показывает аппроксимирующие значения, т.е. функцию Z(x), а ломаная линия – реальные измерениям фигуры в области груди. Невязками называется расстояние между точками на двух графиках, соответствующих одному значению независимой переменной “x”.

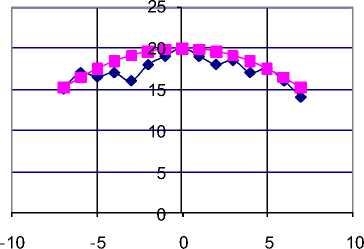
Рисунок 1 – Измеренные значения и аппроксимирующая функция Z(x)

Целевая функция зависит от параметров аппроксимирующей параболы ( P,Zo ) и имеет вид:

n 2

Q (P, Zo) — £ (z-x - Zo )2 =... i=1

n 4

... = E( z 2 + xr+Z i2

i =1

2- o

x ²

2 z ^ - . i_P

..

x_i ² Zo

... — 2 z-Zo + 2      ) — ...

iP

n

... — Ez 2 + i2

i — 1        P

n

... - 2-Y z ^²

P ii

—

n

E x 4 + nz o - ...

— 1

2n                 n x^- - 2 ZoYz, + 2 Zo Yx 2.

p         z—i ¹ p Z—i ¹

P           i — 1           ^P i — 1

Для определения минимального значения целевой функции применяем классический метод частных производных по параметрам от целевой функции:

d Q d P

^™

n

2$ E x 4

^P —1

n

+ ^- У zx ²

2 ii

n

... - 2 Z ^Y x 2 ;

2 i

P— dQ з 7

— 2 nZ_o dZo      ^o

nn

- 2 E z , + 21 E x , i — 1            P i — 1

А.В. Васильева, Е.В.Коваленко, О.А.Кучеренко

Приравнивая производные нулю, получаем систему уравнений:

^d Q = 0;

dP

Q = 0.

5 Z o

Решением системы (10) относительно параметров параболы являются конечные формулы для вычисления со-

ответствующих параметров:

Zo =

n

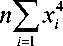
n

- ( Z xf

ди. Т.к. вычисление радиуса кривизны методом наименьших квадратов является достаточно трудоемкой работой даже с использованием вычислительной техники, для расчетов использовался инструмент MS Office «поиск решения», в котором реализованы численные методы оптимизации.

Серия измерений с последующими вычислениями позволила сделать вывод о зависимости радиуса кривизны исследуемой только от формы поверхности, вне зависимости от ее размера.

nn  nn

Z xt Z z-Z x Z z-x-2

i = 1         i = 1            i = 1         i = 1

n

Z x-²

P =     i = 1 _______

n

Z zi- nZo i=1

Радиус кривизны R произвольной линии y=f(x) вычисляется по формуле:

К =

I y "I (1 + y ^,2)^3/2

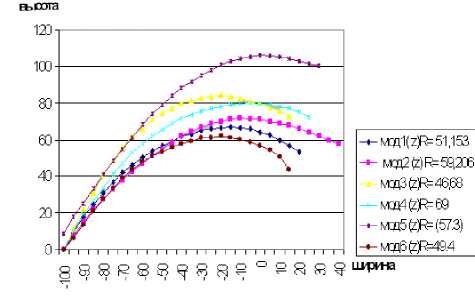
Рисунок 4 - Зависимость величины радиуса кривизны от формы

Радиус кривизны параболы в верхней точке равен: R = P/ 2 т.е R = p. Окружность, соответствующая кривизне поверхности груди, изображена на рис.3. Точка F - фокус параболы, точка С - центр окружности, удаленный от вершины параболы на расстоянии p .

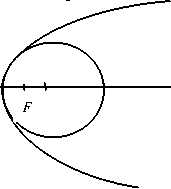
Рисунок 3 - Окружность, соответствующая кривизне поверхности

Радиус кривизны поверхности определялся для различных размеров гру-