Определение диаграмм деформационного упрочнения поверхностных слоев металлических материалов с использованием инструментария наномеханических испытательных комплексов

В связи с миниатюризацией объектов техники, созданием новых микрокомпозиционных, градиентных материалов и покрытий в последние десятилетия отмечается значительный интерес к исследованию механических свойств на субмикро- и наномасштабных уровнях. Одним из фундаментальных механических свойств металлических материалов является их способность упрочняться под действием пластической деформации. Сопротивление пластической деформации обычно характеризуют диаграммами деформационного упрочнения, которые в соответствии с определением должны быть получены в условиях одноосного нагружения. Однако малый размер исследуемых объектов не позволяет применять традиционные методы определения механических свойств, и более перспективными являются методы, основанные на регистрации сопротивления материала локальному воздействию инденторов, используемых при исследовании твердости. При испытаниях на твердость реализуется схема объемного напряженно-деформированного состояния, поэтому диаграмму деформационного упрочнения нельзя непосредственно определить из их результатов. В связи с этим в разное время были предложены соотношения, устанавливающие связь между характеристиками твердости и прочности (А. Бриннель, Р. Бек-лен, С.С. Васаускас, Н.Н. Давиденков, М.С. Дрозд, А.Ю. Ишлинский, A. Крич, М.П. Марковец, В.М. Матюнин, A. Розе, Д. Тейбор, и др.). В дальнейшем, в связи с созданием приборов, позволяющих осуществлять вдавливание индентора с одновременной регистрацией величины нагрузки и глубины вдавливания (метод кинетической твердости), был опубликован ряд работ, связывающих аппроксимацию диаграмм вдавливания с аппроксимацией диаграмм деформационного упрочнения (М.Б. Бакиров, Ж. Букали, М. Дао, А.Е. Джианокополос, Д.А. Коновалов, С.В. Смирнов, А.Н. Солошенко, С. Суреш, Я. Ченг, Н. Чоллокуп, В.П. Швейкин и др.)

В настоящее время созданы наномеханические испытательные системы, основанные на использовании принципа зондовой сканирующей микроскопии, которые позволяют осуществлять программируемое силовое воздействие на поверхность исследуемого материала с нанометровым разрешением. В качестве зонда обычно используются острые трехгранные пирамидальные алмазные инденторы Берковича. Следует отметить, что развитие приборной базы опережает научнометодические разработки, что не позволяет в должной мере использовать возможности зондовых наномеханических систем для определения механических свойств на субмикро- и наномасштабных уровнях.

Необходимость в этих данных связана также и с наблюдаемой тенденцией применения компьютерного проектирования материалов с использованием концептуальных принципов микро(мезо-)механики, в соответствии с которыми возможно осуществлять прогнозный расчет свойств материала, если эти свойства известны на более низких масштабных уровнях.

Целью исследований являлась разработка методики определения диаграмм деформационного упрочнения металлических материалов, которая может быть реализована с использованием технических возможностей зондовых наномеханических испытательных систем по результатам испытаний на вдавливание и царапание индентором Берковича.

Исследуемый материал рассматривается как изотропная упругопластическая и пластически несжимаемая среда с изотропным деформационным упрочнением, для которого справедлив ассоциированный закон пластического течения с функцией текучести Мизеса:

^o i ^{- о} , = о,

где о =лRs S S - интенсивность девиатора напряжений; Si. - компо-i 2 ij ij ненты девиатора напряжений; оs - сопротивление деформации, равное напряжению растяжения (сжатия) при одноосном напряженном состоянии.

Предполагается, что при упругой деформации материал подчиняется закону линейной упругости (2), а на стадии пластической деформации - степенному закону (3), записанным в инвариантной форме:

оi = 2G8, (8 < 8о), (2)

Оi = Оs = a8 , (8 ^ 80), (3)

где 8( t ) = J^ 3 d 8 j d 8 j — степень деформации; d 8 i. = d 8 J + d 8 p , 0

d 8, d 8 T , d 8 p - приращение компонент тензоров полной, упругой и пластической деформаций соответственно; 8 ₀ - степень деформации, при которой материал переходит в состояние пластичности, значение 8 ₀ определяется как ненулевое решение системы уравнений (2) и (3); G - модуль сдвига, связанный с модулем Юнга Е и коэффициентом Пуассона v соотношением G = E2 _{(1 + v}) ; а и b - эмпирические коэффициенты.

Определению подлежат эмпирические коэффициенты а и b . Для их нахождения необходимо иметь как минимум два независимых эксперимента. В качестве таковых были выбраны вдавливание и царапание индентором Берковича по схеме «ребром вперед» при одинаковой нагрузке на индентор. В качестве дополнительного испытания, позволяющего переопределить разрешающую систему уравнений и тем самым повысить точность решения за счет статистического усреднения, использовали испытания на царапание индентором Берковича по схеме «гранью вперед». Значение нормального модуля упругости можно определить экспериментально по методикам [1, 2] или выбрать по литературным данным.

Для разработки методики было выполнено SD-моделирование испытаний на вдавливание и царапание упруго-пластического материала индентором Берковича. Из-за большой размерности задача ре- шалась на кластере ИММ УрО РАН с использованием программы МКЭ ANSYS v.12. Алмазный индентор рассматривали как линейноупругий изотропный материал с модулем Юнга Е = 1140 ГПа и коэффициентом Пуассона v = 0,07. Исходя из типового диапазона дости гаемых нагрузок на современных наномеханических комплексах задавали нагрузку на индентор 5 мН.

С целью рационального расходования машинного времени и целесообразного снижения трудоемкости задачи рассматривали % симметричной композиции (рис. 1).

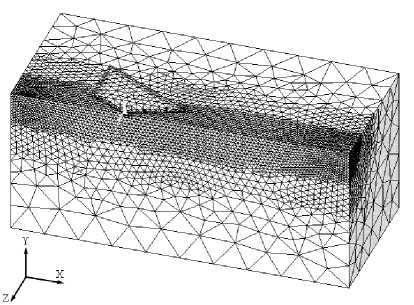
Рис. 1. Конечно-элементная модель

Геометрические размеры моделируемого образца выбирались такими, чтобы пластическая деформация не достигала боковых границ образца. Граничные условия задавали в перемещениях, закрепив от перемещения по всем направлениям нижнюю грань, а одну из торцевых граней образца - от горизонтальных перемещений по оси X . Исходя из условия симметрии плоскость симметрии индентора и образца закрепляли от перемещений по оси Z . Воздействие индентора на материал задавалось равномерным давлением на верхнюю грань индентора.

Для проверки адекватности конечно-элементной модели провели эксперименты по вдавливанию и царапанию индентором Берковича образцов из меди М0. При выборе тестовых экспериментов для проверки адекватности моделирования исходили из того, что при проведении испытаний на микроуровне и ниже возникают принципиальные сложности, связанные с невозможностью изготовления образцов для проведения стандартных механических испытаний на растяжение и сжатие, необходимых для корректного определения функции сопро- тивления деформации, от точности которой зависят результаты моделирования. Кроме того, при микроиспытаниях имеют место неконтролируемые отклонения результатов из-за локальной неоднородности состава и структуры материала, остаточных искажений приповерхностных и поверхностных слоев, возникших при механической обработке и не полностью удаленных при травлении, и др. Поэтому в качестве тестовых экспериментов были использованы макроскопические испытания [3].

Эксперименты на вдавливание проводили на сервогидравличе-ской испытательной машине Instron 8801. Всего было произведено по 10 вдавливаний при максимальной нагрузке на индентор Р = 1 кН. Эксперименты по царапанию были проведены на твердомере Akashi AVK-HF, оснащенном специальным приспособлением для горизонтального перемещения образца. Было произведено 10 экспериментов царапания ребром при нагрузке 10 кг. По усредненным результатам экспериментов были построены диаграмма вдавливания и диаграмма царапания для меди М0. Условия проведения экспериментов были воспроизведены и при моделировании. Кривая упрочнения, которая необходима для конечно-элементной модели, была получена экспериментально из опытов на сжатие этих же образцов. Критерием для проверки адекватности моделирования являлась степень совпадения экспериментальных и расчетных диаграмм вдавливания и царапания. Диаграммы царапания конечно-элементного моделирования и полученные экспериментально хорошо соответствуют друг другу как количественно, так и качественно (рис. 2). Средние относительные отклонения экспериментальных и расчетных диаграмм вдавливания и царапания не превысили 5 %. Экспериментальные данные свидетельствуют о наличии характерных участков изменения глубины проникновения индентора в материал (нырок, всплытие, установившаяся стадия), которые наблюдались при моделировании. Полученные результаты свидетельствует об адекватности моделирования процесса вдавливания и царапания индентором Берковича.

На основании результатов моделирования получили необходимый объем расчетных данных для выбранной совокупности значений коэффициентов а и b. Зависимости глубины проникновения индентора в материал при вдавливании hв и текущей глубины на установившейся стадии царапания Ич от коэффициента а при значениях b = const описали степенной функцией вида h=cad,                               (4)

где коэффициенты аппроксимации c и d приведены в таблице.

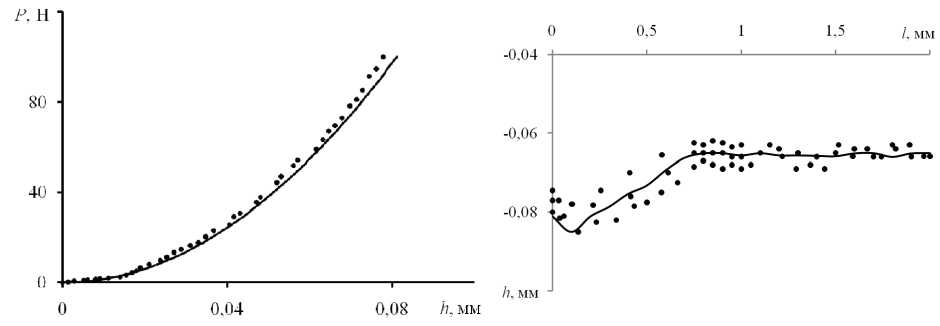
а                                    б

Рис. 2. Сопоставление результатов экспериментов (точки) и моделирования (линии) по вдавливанию ( а ) и царапанию ( б) образцов из меди М0

Последовательность определения сопротивления деформации, описываемой степенной зависимостью (3), заключается в следующем. Для исследуемого материала проводятся эксперименты по вдавливанию и царапанию алмазными инденторами Берковича с фиксированной нагрузкой 5 мН. Затем, при известном из эксперимента значении h в , коэффициентах с и d при разных значениях b из таблицы, по формуле a=(h/c)^d определяются значения коэффициента а .

Коэффициенты аппроксимации зависимости (4)

Коэффициент	Вдавливание		Царапание
b	с , МПа	d	с , МПа	d
0,2	8,4998	–0,474	9,8364	–0,512
0,3	13,441	–0,52	15,562	–0,563
0,4	15,606	–0,511	31,767	–0,657
0,5	19,344	–0,515	46,631	–0,687
0,6	23,582	–0,517	82,403	–0,749

Полученные пары значений a(b) представляют собой возможные сочетания коэффициентов в степенной зависимости (3), которые удов- летворяют условиям данного эксперимента. Зависимость a(b) описывается аналитически или графически. По аналогичному алгоритму определяется зависимость a(b), удовлетворяющая результатам экспериментов по определению величины hц. Общая точка этих зависимостей дает пару искомых значений коэффициентов а и b, определяющих функцию сопротивления деформации для исследуемого материала в виде степенной зависимости (3).

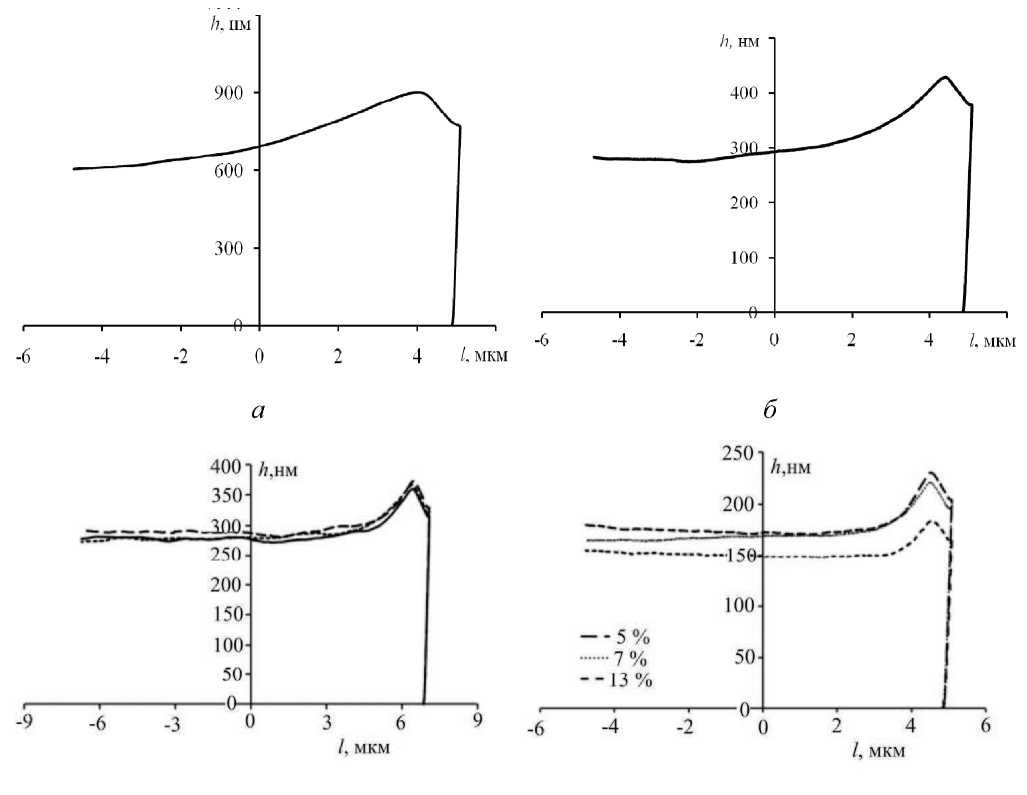
в

г

Рис. 3. Экспериментальные диаграммы царапания при нагрузке 5 мН, полученные при испытаниях на наномеханическом испытательном комплексе Hysitron TI 900 для поверхностных слоев следующих материалов: а - алюминий А0; б - медь М0; в - алюминиевый сплав 01420Т; г - сплав Fe-Cr-Al (Cr - 15 %, содержание Al указано на рисунке, Fe - остальное)

C использованием разработанной методики были выполнены исследования на наномеханическом испытательном комплексе TI 900 и определены диаграммы деформационного упрочнения для поверхностных слоев для ряда металлических материалов; результаты некото- рых из них приведены на рис. 3. Коэффициенты аппроксимации диаграммы деформационного упрочнения в виде степенной зависимости (4) определены по разработанной методике, значения модуля Юнга определены по методике Оливера-Фарра.

Работа выполнена в соответствии с планом исследований интеграционного проекта № 09-С-1-1003 Института теоретической и прикладной механики СО РАН и при финансовой поддержке гранта РФФИ 10-08-96050.