Определение динамических характеристик датчиков быстропеременного давления полулогарифмическим методом

В данной статье предлагается методика определения передаточной функции, временных и частотных характеристик датчиков быстропеременного давления по отклику на ударное воздействие.

Передаточная функция, датчики быстропеременного давления, измерительный эксперимент, аппроксимация.

E. A. Aksenova Akhmetov, I.A. Kruchinin

Senior teacher of the Department "automation and management", student of the Department " automation and management, student of the Department "automation and management».

Penza state technological University Russia, Penza

DETERMINATION OF DYNAMIC CHARACTERISTICS OF SENSORS OF QUICK VARIABLE PRESSURE BY SEMILOGARITHMIC METHOD

The article proposes a method for determining the transfer function, time and frequency characteristics of sensors of fast variable pressure by response to shock

Transfer function, quick-change pressure sensor, measurement experiment, approximation

Существующие на данный , момент методики определения динамических характеристик и измерительных преобразователей основаны на использовании методов непараметрической и параметрической идентификации [1] и требуют проведения сложных измерительных экспериментов.

Представленная методика основана на проведении простейшего измерительного эксперимента и заключается в воздействии на мембрану датчика свободно падающим металлическим шариком с последующей регистрацией выходного сигнала датчика на проведенный механический удар.

На рис. 1 показана осциллограмма выходного сигнала датчика типа ДД1, полученная на запоминающем осциллографе TDS 2012 в результате свободного падения на мембрану датчика металлического шарика диаметром 5 мм, изготовленного из подшипниковой стали, с высоты 155 мм.

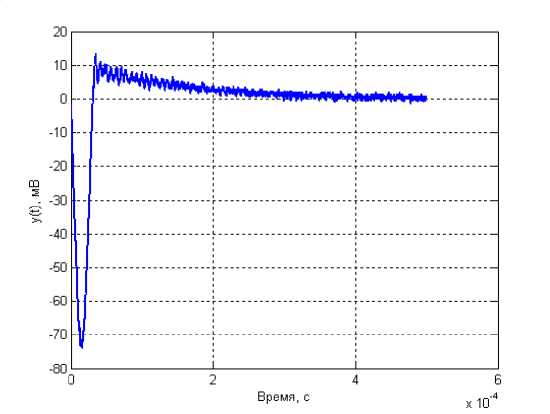
Рис. 1. Осциллограмма выходного сигнал датчика

На рис. 2 представлены оцифрованные через 0,2 мкс значения этой осциллограммы без учета ее начального участка, имеющей большой выброс.

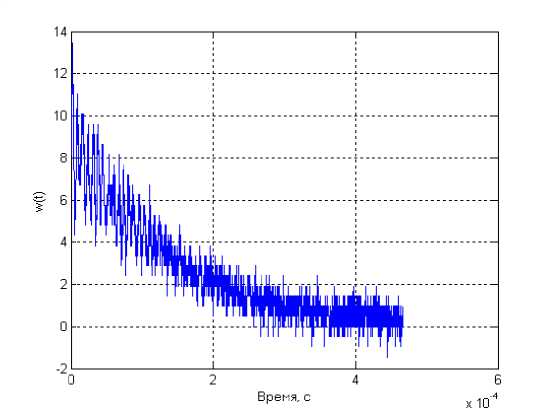
Рис. 2. Экспериментальная импульсная переходная характеристика датчика

В первом приближении такой выходной сигнал будет представлять собой импульсную переходную характеристику и может быть аппроксимирован аналитическим выражением вида n

_Ю (t ) = £ ce p ,                            (1)

г = 1

где C i - постоянные интегрирования, p i - корни характеристического уравнения передаточной функции датчика.

Будем считать, что, выражение (1) имеет три корня характеристического уравнения: один действительный и два комплексно сопряженных. В таком случае (1) запишется так to(t) = Cep1 + C2eа sin(tot + 0)                          (2)

Для нахождения неизвестных параметров в (2) по экспериментальной импульсной характеристике воспользуемся логарифмическим методом [2] в соответствии с которым

z ( 1 ) = ln [ to ( t ) ] = In Ce p ^{1 1} + C₂e " t sin( to t + 0 ) ] .                        (3)

Так как p_x <  a , то выражение z 1( t) = In Ce p ¹ t ] = In C + p_xt                               (4)

будет являться асимптотой (3) при t >^ .

На рис. 3 представлена логарифмическая импульсная характеристика датчика, полученная логарифмированием кривой (рис. 2).

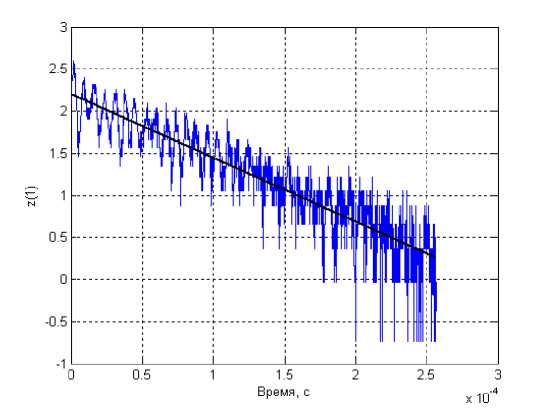
Рис. 3. Логарифмическая импульсная характеристика датчика

Поскольку эта характеристика сильно зашумлена, была проведена ее аппроксимация уравнением прямой (4), по которой были найдены искомые коэффициенты C 1 = 9,0436, мВ ; p 1 = -7.5721 10^-3 с ;

Вычитая из импульсной переходной характеристики (рис. 2) ее первое слагаемое из выражения (2) с найденными коэффициентами C₁ и p₁ получим экспериментальную характеристику (рис. 4), содержащую второе слагаемое выражения (2).

z 2( t) = C^e~^a sin( a t + ф ) . (5)

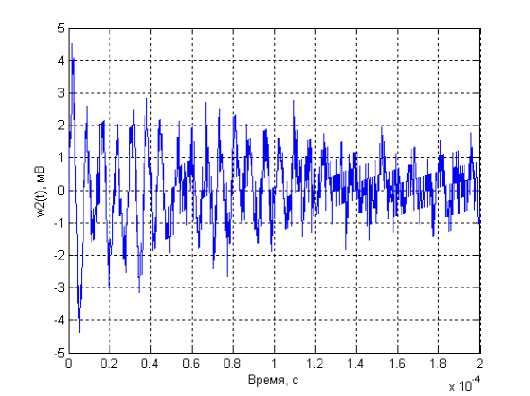
Рис. 4. Экспериментальная временная характеристика z2(t)

Неизвестные коэффициенты   С 2 , α, ω и φ в (5) находятся по методу

наименьших квадратов мимнимизирующем невязку

N ²

5 = ^ [ z 2( t, ) - C^e - ^at i sin( to t_i + ф\ .

i = 1

В результате были найдены следующие значения коэффициентов С₂ = 2,6162 мВ; α = -1,1606 10^-3с; ω = 873011 рад/с; φ = 0,1065 рад.

На рис. 5 показана экспериментальная и рассчитанная по (2) импульсные переходные характеристики датчика. Среднеквадратичное значение ошибки идентификации не превышает 0,6973 мВ.

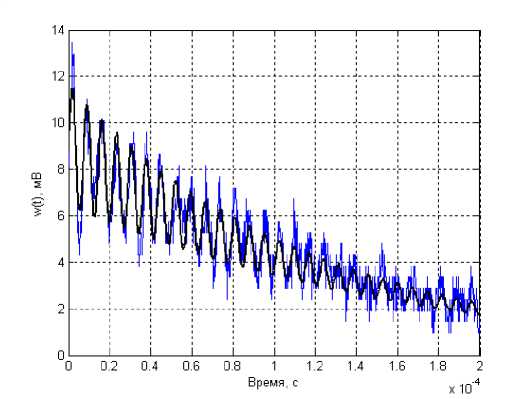
Рис. 5. Экспериментальная и расчетная импульсная переходная характеристика датчика

По расчетной импульсной переходной характеристике датчика была определена его нормированная к единичному коэффициенту передачи передаточная функция

W ( p ) =

( p + 7572)( p ² + 23210 p + 7623 x 10 8 )

По частотной передаточной функции были рассчитаны ЛАЧХ и ФЧХ датчика, приведенные на рис. 6.

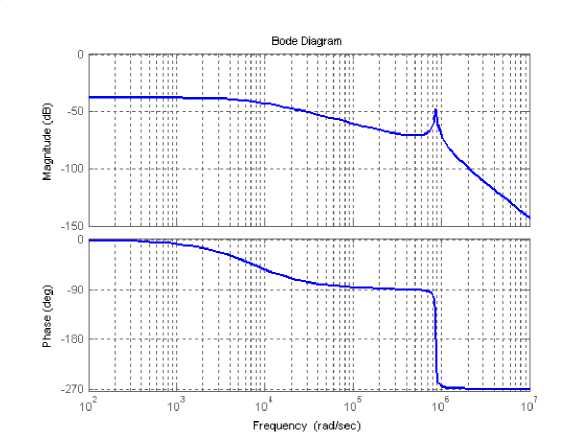
Рис. 6. Расчетные ЛАЧХ и ФЧХ характеристики датчика