Определение динамических характеристик шестерённого насоса по методу вариации нагрузок с использованием специальных стендовых систем
Автор: Санчугов В. И., Рекадзе П. Д.
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 2 т.22, 2022 года.
Бесплатный доступ
Введение. Пульсации рабочей среды в гидросистемах станков, системах топливоподачи авиационных двигателей и подачи жидкостного ракетного двигателя являются одним из главных факторов возникновения вибрации агрегатов, приводящей к усталостному разрушению корпусов элементов, трубопроводов и выходу из строя элементов насосов. Целью работы являлись реализация метода определения динамических характеристик объёмного насоса с использованием специальных стендовых систем и сравнение результатов расчёта с экспериментальными данными. Описаны этапы расчёта динамических характеристик объёмного насоса с учётом разработанных ранее специальных стендовых систем на примере шестерённого насоса внешнего зацепления производительностью 14 см3 /об. Показана реализация метода вариации нагрузок В. П. Шорина с использованием разработанных авторами специальных стендовых систем с заранее определёнными динамическими характеристиками. Излагаются основные этапы методики определения динамических характеристик шестеренного насоса.Материалы и методы. В работе применены методы спектрального анализа пульсирующего давления. Пульсации расхода жидкости на выходе из насоса определялись с помощью импедансного метода, метода вариации нагрузок и специальных стендовых систем.Результаты исследования. В работе реализована методика определения динамических характеристик шестеренного насоса в диапазоне оборотов приводного вала 500-2500 об/мин для четырёх гармонических составляющих спектра колебаний в широком диапазоне динамических нагрузок (от инерционного до емкостного характера). Представлен анализ стендовых систем, приводящих к расчёту динамических характеристик насоса с минимальной погрешностью на основании условия согласования динамической нагрузки и источника колебаний. Проведена проверка разработанного подхода к оценке динамических характеристик насоса посредством сравнения расчётных и экспериментальных данных пульсаций давления в стендовых системах с дросселем, полостью и протяжённым трубопроводом на выходе насоса.Обсуждение и заключения. Реализован метод определения динамических характеристик объёмного насоса с использованием разработанных авторами специальных стендовых систем. Результаты исследований показывают, что исследуемый шестерённый насос может рассматриваться как независимый источник колебаний расхода, для которого отклонение собственных динамических характеристик от средних значений не превышает 10 % по первой гармонической составляющей.
Объёмный насос, метод вариации нагрузок, стендовые системы, источник колебаний расхода, динамические характеристики насоса, независимый источник колебаний, пульсации расхода, импеданс
Короткий адрес: https://sciup.org/142235252
IDR: 142235252 | УДК: 62-19 | DOI: 10.23947/2687-1653-2022-22-2-130-141
Текст научной статьи Определение динамических характеристик шестерённого насоса по методу вариации нагрузок с использованием специальных стендовых систем
Original article
Determination of the dynamic characteristics of a gear pump by the load variation method using special bench systems
Valeriy I. Sanchugov ® , Pavel D. Rekadze В
Introduction. Some of the major factors in the occurrence of vibration of units, causing fatigue failure of the housings of elements, pipelines, and failure of pump elements, are pulsations of the working medium in the hydraulic systems of machine tools, fuel feed systems of aircraft engines and liquid-propellant engine supply. This study aimed at the implementation of a method for determining the dynamic characteristics of a volumetric pump using special bench systems, and the comparison of the calculation results to the experimental data. The stages of calculating the dynamic characteristics of a volumetric pump were described, taking into account the pre-developed special bench systems on the example of an external gear pump with a capacity of 14 cm3/rev. The implementation of V. P. Shorin's load variation method using special bench systems developed by the authors with predetermined dynamic characteristics was shown. The main stages of the methodology for determining the dynamic characteristics of a gear pump were described. Materials and Methods. Methods of spectral analysis of pulsating pressure were applied in the work. Pulsations of fluid flow at the pump outlet were determined using the impedance method, the method of load variation, and special bench systems.
Results. The paper implemented a technique for determining the dynamic characteristics of a gear pump in the drive shaft speed range of 500-2500 rpm for four harmonic components of the vibration spectrum in a wide range of dynamic loads (from inertial to capacitive nature). The bench systems yielding the calculation of the dynamic characteristics of the pump with a minimum error based on the condition of matching the dynamic load and the source of vibrations were analyzed. The developed approach to the evaluation of the dynamic characteristics of the pump was verified through comparing the calculated and experimental data of pressure pulsations in the bench systems with choke, cavity and an extended pipeline at the pump outlet.
Discussion and Conclusions. The method for determining the dynamic characteristics of a volumetric pump was implemented using special bench systems developed by the authors. The research results show that the gear pump under study can be considered as an independent source of flow fluctuations, for which the deviation of its own dynamic characteristics from the average values does not exceed 10% for the first harmonic component.
Машиностроение и машиноведение
Введение. Основные недостатки насосов заключаются в сопровождаемом их работу акустическом шуме, вибрации корпуса, присоединенных трубопроводов и возникающих вследствие этого разрушениях конструкции.
Традиционный путь совершенствования конструкций насосов, используемый в машиностроении и заключающийся в сглаживании неравномерности течения жидкости, затруднен отсутствием средств прямого измерения расхода жидкости на выходе насоса. Это ограничивает любую экспериментальную оценку эффективности конструктивно-доводочных работ по насосам. Кроме того, это ограничивает аналитическое описание насоса как источника колебаний, необходимое разработчикам гидросистем для обеспечения требуемого динамического качества самих систем.
По этой причине исследования, связанные с моделированием динамических процессов в гидромеханических системах [1, 2] и применением новых подходов к решению задач динамики гидравлических систем [3, 4] на основе физических принципов, имеют актуальность.
Материалы и методы. Представлена реализация метода вариации нагрузок В. П. Шорина [4] , заключающаяся в том, что определяются пульсации давления за насосом, взаимодействующим с несколькими стендовыми системами, динамические характеристики которых рассчитаны заранее. Далее обработанные амплитудно-частотные характеристики давления с использованием импеданса стендовых систем пересчитываются в собственные динамические характеристики насоса — пульсационную производительность и импеданс. Развитие подхода состоит в том, что предложены специальные стендовые системы, учитывающие соединительные штуцеры, переходники и внутренние каналы насоса, что позволяет точнее определять динамические характеристики насосов, а также осуществлять проверку применимости используемой модели насоса в виде эквивалентного источника колебаний.
Результаты исследования
Методика определения динамических характеристик шестеренного насоса
В Самарском университете разработана расчетно-экспериментальная методика определения динамических характеристик шестеренного насоса (пульсационной производительности и импеданса), которая базируется на исследованиях Л. Тевенена, Э. Нортона и В. П. Шорина [5, 6]. Разработанная методика включает в себя следующие основные этапы: создание моделей и расчет динамических характеристик специальных стендовых систем; экспериментальное определение пульсаций давления на выходе насоса; расчет спектра возбуждаемых колебаний в различных стендовых системах; определение аппроксимирующих зависимостей для отдельных гармонических составляющих; расчёт собственных динамических характеристик насоса (пульсационной производительности и импеданса); оценка независимости (стабильности) динамических характеристик насоса от характеристик стендовых систем; проверка применимости используемой модели насоса в виде эквивалентного источника колебаний расхода (или давления). Далее приведен пример реализации предложенной методики с использованием шестерённого насоса внешнего зацепления удельной производительностью 14 см3/об.
Модели и расчет динамических характеристик специальных стендовых систем
Рассмотрены базовые варианты стендовых систем на выходе жидкости при испытаниях насосов. В сосредоточенных параметрах стендовая система может реализовывать активную расходно-зависимую, инерционную и упругую нагрузки. В распределённых параметрах стендовая система может быть реализована в виде протяжённого цилиндрического трубопровода, реализующего активную частотно-независимую неотражающую нагрузку.
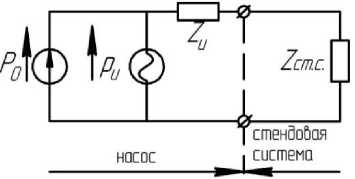
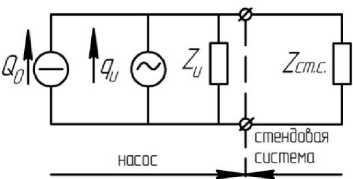
Модели насоса в виде эквивалентных источников колебаний расхода (ЭИКР) или давления (ЭИКД) определяются с использованием источника постоянного расхода Q , идеального источника колебаний давления p (или расхода q ) и внутреннего импеданса Z [4] . На рис. 1 представлены модели насоса в виде эквивалентного источника колебаний давления (и расхода) с присоединенной системой.
а )
Рис. 1. Модели насоса в виде эквивалентного источника колебаний: а — давления; б — расхода с присоединенной системой: Q , P — средний расход и давление; p , q — собственная пульсационная производительность насоса по
б )
давлению и расходу, Z , Z — импеданс насоса и стендовой системы (адаптировано из [4] )
При этом задачей выбора стендовой системы является обеспечение таких параметров системы, при которых реализуются наилучшие условия высокой точности измерений. Задачу выбора параметров присоединенной системы необходимо проводить при изменении импеданса в диапазоне от -∞ до +∞.
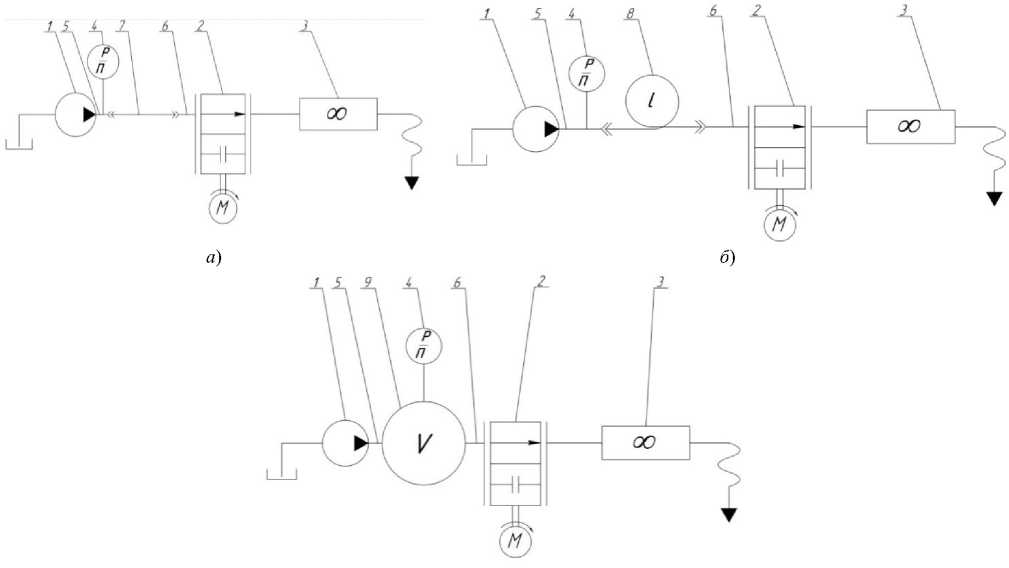
Принципиальные схемы стендовых систем представлены на рис. 2.
в )
Рис. 2. Принципиальные схемы стендовых систем для определения собственных динамических характеристик насосов: а — с активной дроссельной нагрузкой; б — с активной неотражающей нагрузкой; в — емкостной нагрузкой:
1 — испытуемый насос; 2 — нагрузочный дроссель; 3 — расходомер; 4 — датчик давления; 5, 6 — соединительные штуцеры; 7 — магистраль; 8 — протяжённый трубопровод; 9 — полость
Расчётные модели импедансов специальных стендовых систем: – с активной дроссельной нагрузкой (дроссель):
Z ст . с . к
Г
( Q o , f К, ( Z gp ( Q o ) + ReZ тр ( Q o ) )2 + 2 n fk \ ^ S тр J
- 2 nfk ^^
Sтр jarctg , e Zgp (Qo)+ReZmp (Qo)
– с активной распределенной нагрузкой (протяжённый трубопровод):
p a
Zcm. c. ’ тр
– с емкостной нагрузкой (полость):
Z cmc . k ( Q o , f k ) = . ( ReZ лам ( Q o ) + ReZ myp6 ( Q o ) + ReZ мс. ( Q o ) + Z gp ( Q o ) ) 2
jarctg I
*e '
( 2 - ft ) 2 LC - 1
2 - f k C ( ReZ лам + ReZ myp6 ( f k ) + ReZ м.с. ( f„ ) + Z gp ( Q „
( 2 n f k ) 2 LC - 1 2 n f k C
*
В формулах обозначены: Zdp ( Q o) — импеданс дросселя; ReZm ( Q o) — действительная часть импеданса трубопровода, включающего соединительную магистраль, штуцеры, внутренние каналы в насосе и дросселе; ReZp ^ ( Q o) , ReZmyр6 ( Q o) , ReZ„ с ( Q o) — действительная часть импеданса штуцеров и внутреннего канала в насосе и полости при ламинарном, турбулентном течении жидкости за насосом и местных сопротивлениях
соответственно; f — частота k - й гармонической составляющей спектра колебаний за насосом; р
—
плотность рабочей среды; l — длина трубопровода, включающая длину магистрали 6, соединительных штуцеров 5 и 7 и внутренних каналов насоса и дросселя (не показаны на рис. 7); S — площадь поперечного сечения трубопровода; L — «инерционность» соединительных штуцеров и внутреннего канала в насосе и полости; С — упругость полости; k — номер гармонической составляющей спектра колебаний; j — мнимая единица ( j = V-1).
Машиностроение и машиноведение
С использованием стендовой системы с дросселем на выходе насоса реализованы три инерционно-активные динамические нагрузки, в которых изменялось активное сопротивление изменением площади перекрытия дросселя F0:
– для стендовой системы №1 площадь перекрытия F01=9,290×10-6 м2,
– для стендовой системы №2 площадь перекрытия F02=7,299×10-6 м2,
– для стендовой системы №3 площадь перекрытия F03=2,247×10-5 м2.
С использованием стендовой системы с полостью на выходе насоса объёмом 2 л реализована инерционноупругая динамическая нагрузка.
С использованием стендовой системы с протяжённым трубопроводом длиной 106 м реализована активная частотно-независимая нагрузка.
По моделям стендовых систем по формулам (1)–(3) рассчитаны зависимости импеданса (модуля и фазы) от частоты. В таблице 1 для 1-й гармоники приведены функции регрессии модуля импеданса стендовой системы Zi(f) и фаз βi(f) для анализируемых стендовых систем.
Таблица 1
Функции регрессии динамических характеристик стендовых систем по 1-й гармонике
|
№ стендовой системы по рисунку 2 |
Тип стендовой системы |
Модуль импеданса стендовой системы кг Z i (f), 42 мс |
Фаза импеданса стендовой системы β i (f), рад |
|
а – №1 |
С дросселем на выходе насоса |
1,412·107f + 2,201·109 |
7,066·10-4f + 0,199 |
|
а – №2 |
1,610·107f + 4,258·109 |
6,906·10-4f +0,09039 |
|
|
а – №3 |
4,980·107f + 1,503·109 |
2,723·10-3f + 0,251 |
|
|
б – №4 |
С полостью на выходе насоса |
3,308·104f2 – 1,416·107f + 1,873·109 |
, 4,234 - 10 6 f + 1,495 - 10 9 х arctg () 1,43 0 - 10 5 f + 2,930 - 10 6 |
|
в – №5 |
С протяжённым трубопроводом на выходе насоса |
1,897·1010 |
0 |
Экспериментальное определение пульсации давления на выходе насоса
Исходной информацией для определения динамических характеристик насоса являлось измерение давления на выходе насоса. Пример осциллограммы и спектра пульсаций давления на выходе из насоса в стендовой системе с активной распределенной нагрузкой представлены на рис. 3. Режим работы насоса при этом: среднее давление Po = 23,8 МПа , частота вращения приводного вала n = 1000 об / мин .
0,42
0,35
0,28
0,21
0,14 б
0,07
с
0,00
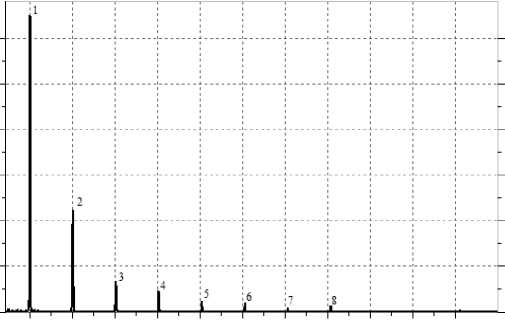
167 334 501 668 835 1002 1169 1336 1503 1670 1837
Частота составляющих спектра колебаний, Гц
б )
Рис. 3. Давление на выходе насоса: а — осциллограмма; б — спектрограмма
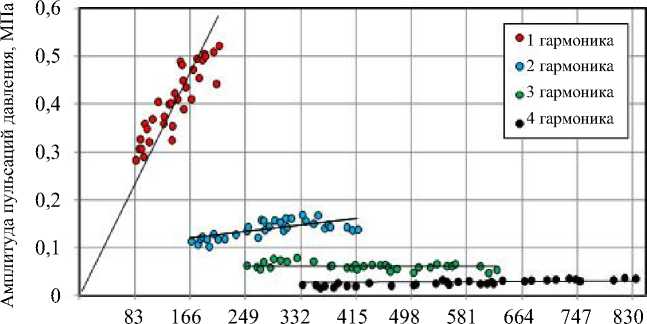
Амплитудно-частотная характеристика пульсаций давления на выходе насоса в диапазоне оборотов приводного вала насоса n=500–1250 об/мин представлена на рис. 4. Сплошной линией нанесены функции регрессии, построенные в среде Microsoft Excel при помощи инструмента «Линия тренда».
Частота составляющих спектра колебаний f3, Гц I---------------------1--------------------1----------------------1
0 500 1000 1500
Частота вращения приводного вала n, об/мин
I— г1 т - 1 0 7,3 14,6 21,6
Средний расход жидкости насоса Q, л/мин
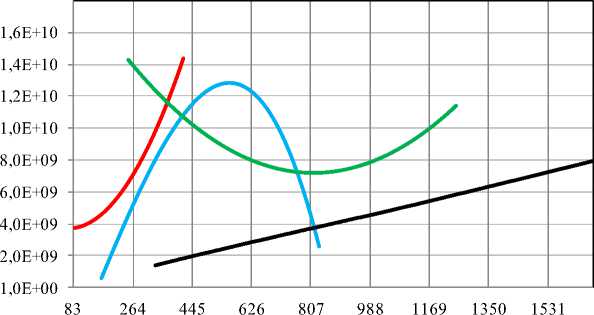
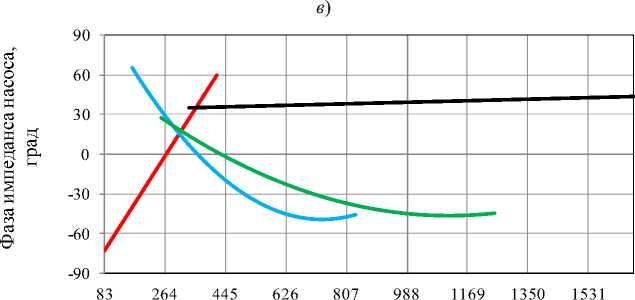
Рис. 4. Амплитудно-частотная характеристика пульсаций давления на выходе насоса по отдельным гармоническим составляющим (точками обозначены данные на: — первой, — второй, — третьей, — четвёртой гармониках, линиями обозначены функции регрессии)
Анализ осциллограммы, спектрограммы и амплитудно-частотной характеристики пульсаций давления показал следующее: тип процесса полигармонический установившийся; число регистрируемых гармоник — 8, анализируемых1 — 4; диапазон амплитуд колебаний давления 0,28–0,52 МПа; частотный диапазон приводного вала 500–1250 об/мин, анализируемых гармонических составляющих спектра 83–833 Гц.
Для гармонического анализа периодических сигналов использовалось разложение в ряд Фурье [7]. Для разложения в ряд Фурье использованы участки осциллограммы давления, измеряемые относительно опорного сигнала на роторной частоте, т.е. за полный оборот ротора извлекался один участок осциллограммы. Опорный сигнал регистрировался при фиксированном положении шестерни, выставляемом при начале записи осциллограммы давления для пяти стендовых систем. Таким образом определялись амплитудно-частотные (АЧХ) Ak ( ю ) и фазо-частотные (ФЧХ) фк ( ю ) характеристики.
Машиностроение и машиноведение
Расчет спектра возбуждаемых колебаний в различных стендовых системах и определение аппроксимирующих зависимостей для отдельных гармонических составляющих колебаний давления
На основе экспериментального определения давления в пяти стендовых системах: с дросселем (№1–3), с полостью (№4) и протяжённым трубопроводом (№5) на выходе насоса рассчитаны спектры возбуждаемых колебаний. В таблице 2 приведены функции регрессии амплитуд Ap(f) и начальных фаз пульсаций давления для 1-й гармоники.
Таблица 2
Функции регрессии амплитуд и начальных фаз пульсаций давления
|
№ стендовой системы по рисунку 2 |
Тип стендовой системы |
Амплитуда пульсаций давления кг A pi (f), мс |
Начальная фаза пульсаций давления φ i (f), рад |
Частотный диапазон |
|
а – №1 |
С дросселем на выходе насоса |
1,003·10-3f |
–0,543 |
83–417 |
|
а – №2 |
1,243·10-3f |
–0,280 |
||
|
а – №3 |
6,129·10-4f |
–5,941 |
||
|
б – №4 |
С полостью на выходе насоса |
1,343·10-6f2 – 4,298·10-4f + 3,913·10-2 |
–5,373 |
|
|
в – №5 |
С протяжённым трубопроводом на выходе насоса |
2,694·10-3f |
–0,658 |
Расчёт динамических характеристик насоса
Для расчета динамических характеристик насоса (импеданса и пульсационной производительности источника) необходимо провести эксперимент как минимум с двумя динамическими нагрузками2. При этом импеданс насоса по уточнённой авторами модели эквивалентного источника колебаний расхода с использованием аналитических зависимостей p, ( f ) и Z ( f ) из таблиц 1 и 2 рассчитывается по формуле:
1 - p-
Z u = Z i ^ p/ , (4)
p 1 Z 1
p 2 Z 2
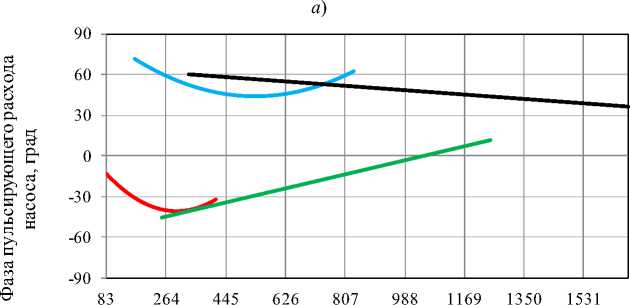
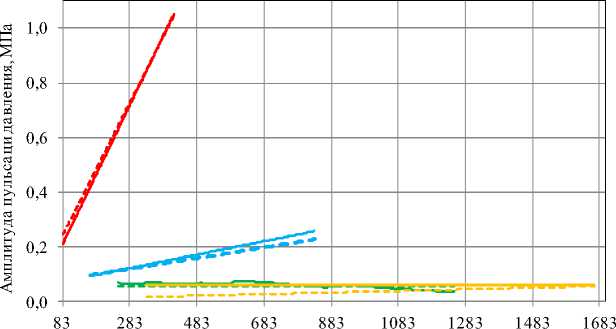
где Zu — импеданс насоса (Zu = |Zu|eM) — модуль импеданс насоса (|Zu| = JReZИ2 + ImZИ1 ), ReZu,ImZu — действительная и мнимая часть импеданс насоса, фи — аргумент импеданса насоса, Zx, Z2 — входной импеданс динамических нагрузок № 1-2 (Zx = iZjej'^, Z2 = |Z2|eje2), в,в — аргументы импедансов динамических нагрузок № 1–2, p, p — пульсации давления за насосом в стендовой системе № 1–2 ( px = ApXeM, p2 = Aplej Затем с использованием аналитических зависимостей из таблиц 1, 2 определяется пульсационная производительность насоса по уточнённой авторами модели эквивалентного источника колебаний (переменная составляющая объёмного расхода q и давления p ): 1 - p2 Z D = Z ! P2 Pu Pi Z1 p1 p2 где qu,pu — переменная составляющая объёмного расхода (q„ = A^ej") и давления (pu = Apuejp ) насоса, Aqu, Apu — амплитуда пульсаций расхода и давления насоса, фч, фp — аргумент переменной составляющей объёмного расхода и давления насоса. Из рассчитанных характеристик по модели ЭИКР (qu (f)) и ЭИКД (pu (f)) по формуле (5) только одна будет отличаться стабильностью, т.к. эквивалентный источник колебаний имеет независимую динамическую характеристику только по одному из параметров (пульсирующий расход или давление). Расчет импеданса Z и переменной составляющей объёмного расхода q насоса по формулам (4)–(5) проведён для пяти динамических нагрузок, т.е. с использованием десяти различных комбинаций этих нагрузок: «1_2», «1_3», «2_3», «1_4», «2_4», «3_4», «1_5», «2_5», «3_5», «4_5» (см. таблицу 1). Для дальнейшего расчёта и анализа из десяти кривых амплитуд пульсаций расхода получена характеристика амплитуд пульсаций расхода насоса A . Значения амплитуд A (на каждой частоте) рассчитывались по формуле из источника [8]: Aqu = Aqu A Aqu , где Aqu — средняя амплитуда пульсирующего расхода, AA— доверительный интервал амплитуды пульсаций t^ расхода насоса (AA= —=), ст — среднеквадратическое отклонение амплитуды пульсирующего расхода от m среднего значения, m — число комбинаций динамических нагрузок (m = 10), t — коэффициент Стъюдента ( t = 2,262, рассчитан для доверительной вероятности 0,95). Доверительный интервал амплитуд AAформируется из погрешностей (инструментальной и методической) и степени зависимости динамической характеристики насоса Aq (f) от стендовой системы. Инструментальная погрешность состоит из погрешности определения давления и фаз, методическая погрешность состоит из погрешности неучтённого влияния динамических свойств приводной механической системы. Фазы пульсаций расхода ^ и их отклонения рассчитывались аналогичным образом. При расчёте фаз комбинации «1_2» и «1_5» исключены по причине вырождения переменной составляющей объёмного расхода насоса qu при использовании близких значений характеристик на одной частоте: ^ ~ ^и Д ~ в ■ Результаты р ё б й й е пульсационной производительнос радусах. Частота гармонических составляющих спектра колебаний, Гц Частота гармонических составляющих спектра колебаний, Гц б) Машиностроение и машиноведение Частота гармонических составляющих спектра колебаний, Гц Частота гармонических составляющих спектра колебаний, Гц г) Рис. 5. Динамические характеристики насоса: а — амплитуда пульсаций расхода; б — фаза пульсаций расхода; в — модуль импеданса; г — фаза импеданса (сплошными линиями обозначены данные по: — первой; ^^^^^n — второй; ^^^^^^» — третьей; — четвёртой гармониках) Амплитуда пульсаций расхода на 1-й гармонике имеет монотонно возрастающий характер. С увеличением номера гармоники наклон кривой амплитуд пульсаций расхода снижается до практически постоянного значения к 4-й гармонике. Значения амплитуд A на высших гармониках на порядок меньше, чем на 1-й гармонике. Модуль импеданса насоса на 1-й гармонике имеет монотонно возрастающий характер. Для оценки реализованных динамических нагрузок использован критерий согласования модуля импеданса Z источника колебаний и входного модуля импеданса динамической нагрузки Zст.с [99, 10]. Модули импедансов должны быть сравнимы ( Z≅Z ), чтобы количественные значения динамической характеристики насоса определялись с минимальной погрешностью. Для сравнения использовано отношение Zи Zст.с. . При Zи Zст.с. ≅ 1 динамическая нагрузка считается согласованной с источником. Ввиду различия форм кривых модулей импеданса насоса и динамических нагрузок в диапазоне частот 83– 417 Гц рационально использовать среднее отношение части частотного диапазона. Т.е. отношение Zи Z ст.с. Zи Zст.с. min…fmax max , которое позволит учитывать вклад большей по 1-й гармонике составит: – для активной дроссельной нагрузки №1 —1,16; – для активной дроссельной нагрузки №2 —0,8; – для активной дроссельной нагрузки №3 —2,65; – для емкостной нагрузки №4 — 4,64; – для активной распределенной нагрузки №5 — 0,35. Т. е. динамические нагрузки стендовых систем №1, 2 являются наиболее согласованными с источником колебаний. Таким образом, динамическая характеристика насоса, рассчитанная с использованием динамических нагрузок стендовых систем №1, 2 («1_3», «2_3», «1_4», «2_4», «1_5», «2_5») определена с минимальной погрешностью. Оценка стабильности динамических характеристик насоса от характеристик стендовых систем Стабильность динамических характеристик A и ϕ ( Z и ϕ ) насоса оценивалась с использованием инструментов математической статистики [8]. Так стабильность характеристики A оценена через расчёт отношения доверительного интервала ΔAqи на частоте f к среднему значению характеристики AqиМе на этой частоте3. Полученное относительное отклонение Δ не должно превышать заданное отклонение Δ : Δq ΔA qи < Adonq , A qиМе где AqиМе — среднее медианное значение амплитуды пульсаций расхода насоса; Δ — задаваемое относительное отклонение амплитуды пульсаций расхода насоса от среднего значения. При относительном отклонении A, ^ 0 (когда AAqu ^ 0) стабильность характеристики Aqu максимальна. Исходя из опыта других исследователей, предпочтительно выбирать величину Δ в пределах 5–30 % [11–17]. Для одночисловой оценки динамических характеристик насоса рационально использовать величину относительного отклонения. Расчёт такой величины возможен по оценке среднего медианного значения относительных отклонений в диапазоне частот каждой гармоники ( f…f): Δ ΔA qи Aqи Величину max ΔqМe ΔAqи рационально использовать, если Aqи < 0,3 , т.е. когда доверительный интервал AAди не превышает max 30 % от средней амплитуды пульсирующего A . Результаты оценки стабильности динамических характеристик насоса от характеристик стендовых систем4 составляют: по 1-й гармонике — 2 %, по 2-й — 8 %, по 3-й — 15 %, по 4-й — 48 %. Результаты расчёта динамических характеристик насоса показали, что по четырём гармоникам в диапазоне частот 500–2500 об/мин исследуемый шестерённый насос целесообразно рассматривать по модели эквивалентного источника колебаний расхода. Проверка применимости используемой модели насоса в виде эквивалентного источника колебаний расхода Для проверки разработанного подхода оценки динамических характеристик насоса было выполнено расчётное определение пульсаций давления в стендовых системах с дросселем, полостью и протяжённым трубопроводом на выходе насоса. С использованием найденных динамических характеристик насоса рассчитаны амплитуды пульсаций давления в анализируемых стендовых системах, которые сравнивались с экспериментальными. Ниже представлены результаты расчёта амплитуд A( f) в стендовой системе с протяжённым трубопроводом. Амплитуды пульсаций давления p рассчитаны в соответствии с моделью ЭИКР по формуле: qи⋅Zи⋅Zi (6) p Zu + Z ’ Результаты расчёта амплитуд пульсаций давления за насосом приведены на рис. 6. Пунктирной линией обозначены амплитуды, полученные экспериментально, а сплошной линией — рассчитанные по формуле (6). Машиностроение и машиноведение Частота гармонических составляющих спектра колебаний, Гц Рис. 6. Амплитудно-частотная характеристика давления для стендовой системы с протяжённым трубопроводом длиной l=106 м (сплошными линиями обозначены расчётные данные по: — первой; — второй; — третьей; — четвёртой гармониках; пунктирными линиями обозначены экспериментальные данные) Оценка сходимости результатов проверочного расчёта проведена по формуле отклонения разницы экспериментальных и расчётных значений от экспериментальных данных. Результаты проверочного расчёта для стендовых систем с дросселем, полостью и протяжённым трубопроводом на выходе насоса показали, что по 1-й гармонике относительное отклонение от экспериментальных данных для рассмотренных стендовых систем не превышает 10 %, минимальное относительное отклонение характерно стендовой системе с протяжённым трубопроводом на выходе насоса — 2%. Амплитуды пульсаций давления 2-й–4-й гармоник находятся в пределах коридора, рассчитанного по формуле Л = Л ± Л (где Лр — средняя амплитуда пульсирующего давления). Обсуждение и заключения. Реализована методика расчёта динамических характеристик насоса в виде эквивалентного источника колебаний расхода жидкости на примере шестерённого насоса производительностью 14 см3/об с использованием разработанных авторами специальных стендовых систем и уточнённой модели импеданса и пульсационной производительности по расходу. Показано, что исследуемый шестерённый насос внешнего зацепления рационально рассматривать по модели эквивалентного источника колебаний расхода. Проведена проверка предлагаемого подхода в виде расчёта амплитуд пульсаций давления в стендовых системах и сравнения с экспериментальными значениями. Отклонение расчётных амплитуд пульсаций давления от экспериментальных значений не превысило 10 %. Стоит отметить, что за рамками обзора осталось влияние на динамические характеристики шестерённого насоса приводной механической системы и износа деталей шестерённого насоса. На основе проведённой работы можно сформулировать направления развития предлагаемого подхода: – оценка динамических характеристик шестерённого насоса в течение всего срока службы; – разработка четырёхполюсной модели шестерённого насоса как эквивалентного источника колебаний, учитывающей приводную механическую и выходную гидравлическую системы; – разработка модели шестерённого насоса как эквивалентного источника колебаний, учитывающей его конструктивные особенности, процесс вытеснения, обратный гидроудар в межзубовую камеру, работу запертого объёма и перетечки из области нагнетания в область всасывания. При этом для подтверждения работоспособности предлагаемого подхода на весь класс машин объёмного вытеснения необходимо расширение номенклатуры испытуемых объёмных насосов.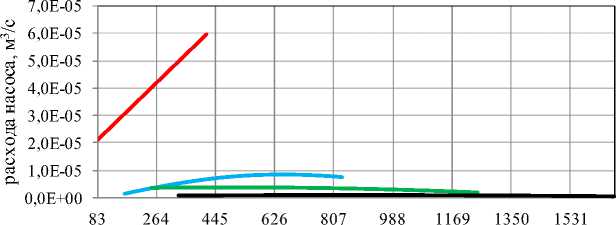
Список литературы Определение динамических характеристик шестерённого насоса по методу вариации нагрузок с использованием специальных стендовых систем
- Рыбак, А. Т. Моделирование и экспериментальные исследования гидромеханической системы со знакопеременной нагрузкой / А. Т. Рыбак, В. П. Жаров, Р. А. Фридрих // Вестник Донского государственного технического университета. — 2006. — Т. 6, № 1. — С. 17-25.
- Рыбак, А. Т. Объемная жесткость и ее влияние на динамику гидромеханической системы / А. Т. Рыбак // Вестник Донского государственного технического университета. — 2006. — Т. 6, № 3. — С. 200-207.
- Озерский, А. И. Применение подхода Лагранжа к решению задач динамики гидравлических систем гидроприводных и теплоэнергетических установок / А. И. Озерский // Вестник Донского государственного технического университета. — 2010. — Т. 10, № 6. — С. 914-925.
- Формирование динамических свойств трубопроводных цепей / Н. Д. Быстров, А. Г. Гимадиев, А. Н. Головин [и др.]; под ред. В. П. Шорина. — Самара : Изд-во Самар. ун-та, 2020. — 328 с.
- The equivalent circuits Thévenin and Norton / M. Staniloiu, H. Popescu, G. Rezmeri^a, M. Iordache // The Scientific Bulletin of Electrical Engineering Faculty. — 2021. — Vol. 21. — P. 40-48.
- Thévenin, L. Sur un nouveaux théorème d'électricité dynamique / L. Thévenin // Comp. Rendus hebdomadaires des Séances de l'Académie des Sci. — 1883. — Vol. 97. — P. 159-161.
- Generalized Functions and Fourier Analysis / M. Oberguggenberger, J. Toft, J. Vindas, P. Wahlberg (ed.) — Springer International Publishing AG, 2017. — 276 p.
- Handbook of Mathematics, 5th ed. / I.N. Bronshtein, K.A. Semendyayev, G. Musiol, H. Muhlig. — Berlin: Springer, 2015. — 1207 p.
- Артюхов, А. В. Особенности частотных испытаний гидравлических насосов / А. В. Артюхов, Л. И. Брудков // Вибрационная прочность и надежность двигателей и систем летательных аппаратов: межвуз. сб. науч. тр. — Куйбышев : КуАИ, 1982. — Вып. 9. — С. 12-17.
- Sundararajan, D. Introductory circuit theory / D. Sundararajan. — Switzerland : Springer, 2020. — 297 p. https://doi.org/10.1007/978-3-030-31985-4
- Ichiyanagi, T. The temperature characteristics of flow ripple and source impedance in an external gear pump / T. Ichiyanagi, T. Nishiumi, Sh. Nakagawa // In: Proc. 10th JFPS Int. Symposium on Fluid Power, 2017. — 5 p.
- Артюхов, А. В. Методика определения динамических характеристик гидравлических насосов / А. В. Артюхов, В. П. Шорин // Динамические процессы в силовых и энергетических установках летательных аппаратов аппаратов: межвуз. сб. науч. тр. — Куйбышев : КуАИ, 1988. — С. 70-77.
- Jinghao Liu. Source flow ripple and source impedance measurement for different hydraulic pumps / Jinghao Liu // In: Proc. 47th Int. Congress and Exposition on Noise Control Engineering (InterNoise 2018). — Chicago, Illinois, 2018. — 7 p.
- Liselott Ericson. On Fluid Power Pump and Motor Design - Tools for Noise Reduction. PhD Thesis / Liselott Ericson. — Linkoping University, Sweden, 2011. — 130 p.
- Bramley, C. Comparison of methods for measuring pump flow ripple and impedance / C. Bramley, D. N. Johnston // In: Proc. ASME/BATH 2017 Symposium on Fluid Power and Motion Control. — 2017. — 11 p. http://dx.doi.org/10.1115/FPMC2017-4223
- Jinghao Liu. Hydraulic Fluid-Borne Noise Measurement and Simulation for Off-Highway Equipment / Jinghao Liu, Sanghoon Suh, Yuzhen Yang // In: Proc. 2017 SAE/NOISE-CON Joint Conf. (NoiseCon 2017), Grand Rapids, MI. —2017. — Vol. 9. — P. 435-443.
- Theoretical and experimental studies of a switched inertance hydraulic system including switching transition dynamics, non-linearity and leakage / Min Pan, Nigel Johnston, Andrew Plummer [et al.] // Proc. Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering. — 2014. — Vol. 228. — P. 802-815. https://doi.org/10.1177/0959651814548299


