Определение динамической прочности трубы, нагруженной быстроперемещающейся радиальной нагрузкой

Поверхности внутренних каналов газодинамических устройств, особенно работающих в условиях импульсного нагружения, могут подвергаться быстроизменяющимся или кратковременным импульсам давления. Импульс формируется, например, при сгорании твердого или жидкого топлива в газодинамических импульсных устройствах, при детонации топливно-воздушной смеси в ДВС и в других случаях. Образующийся фронт импульса может распространяться с переменной скоростью вдоль поверхности канала, достигая значений, превышающих тысячу метров за секунду, а давление во фронте иногда достигает значений, сравнимых с пределом выносливости материала. Наличие импульса давления приводит к появлению в каналах динамических эффектов, снижающих запасы прочности, которые необходимо учитывать на этапе проектирования подобных устройств.

Впервые оценка динамического коэффициента при подвижной нагрузке была проведена Ильюшиным А.А., Огибаловым П.М. [1], на основании решения уравнения вынужденных радиальных колебаний полого цилиндра, под действием внутреннего давления p и кольцевого давления Q = qc , движущихся с постоянной скоростью v вдоль цилиндра вправо, при условии, что давление справа от Q равно нулю (рисунок 1):

8 2 w     д4 w   ( 2 цD     Р ^ д 2 w р h        + D        + I          —         I        + ...

8t²       8%⁴     у R²      2 n R J дx²

12(1 — ц 2 ) D           ц Р

... + -----~----w = P — ----Г’ h 2 R 2               2 n R 2

где w - радиальный прогиб; h = b — a - толщина стенки, R = 0 , 5 ■ (a + b) - радиус срединной

pR ²

где p =-----;

Eh

3          _____ q = — = 44У3(1 D

—

₂ qcR

Ц ) -----

Eh

^Rh  ^;

22 ph ц l

X = -------

4 D

намичности;

^— ц

c      р

Eh поверхности, d = ---------, р

12 ( 1 — ц ² )

постоянная

2 . ^R ( v )      _       _  _

) — |   |  - параметр ди- h У c J

– скорость звука в стенке

трубы, c – скорость распространения звука в

металле; e - модуль упругости; i =

⁴ 3 ( 1

ц ² )

– характерный размер области изменения де-

формаций; — <  a = arctg

—

^{1 +} X

<

у

^{1 —} X J

3 п

--= A

осевая растягивающая сила, p – внутреннее давление; ц - коэффициент Пуассона; р -плотность материала цилиндра.

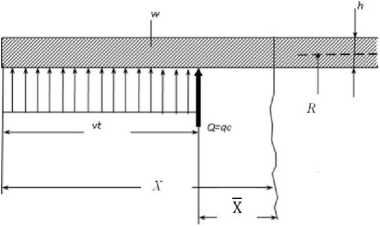
Рисунок 1 – Труба под действием постоянного давления p и кольцевого давления Q = qc , движущихся со скоростью v = const вдоль трубы вправо

Рассматривая стационарное решение, неизменное в осях, движущихся вместе с нагрузкой, Ильюшиным А.А. получены выражения для определения прогиба ( w ) и динамического коэффициента ( k ) при действии толь- ко внутреннего давления p и отсутствии кольцевого давления Q и осевой силы P:

p     Г —a⁽            X г    ^1

w max = —i=\²^^{2 +} e I V ^{1 —} X ⁺----- V^{1 +} X I I ,

2-42 [             у            1 — X          J J k - =

дp

²^ + e ~⁴⁽7 1 ^— x ⁺   x— ¹ + x )

^{1 —} X

2jl + e ~4

и при действии только кольцевого давления Q :

При x < 1 за счет динамичности нагрузки прогиб w будет больше, чем при статическом ее приложении (х = о), и потому коэффи- циент динамичности определяется как отношение максимального прогиба wm„ при x > о к максимальному прогибу при х = о:

⁽ w max ) х > 0

k_B =--------- , где статический прогиб обо-

⁽ w max ) % = 0

лочки     по     безмоментной     теории

• 1    l 4          Ц Р

w ст =-- ⁽ p --Г ) .

• 4    D      2 п R ²

Значение параметра х = 1 определяет критическую скорость движения нагрузки v , при которой возможно сильное влияние ее динамичности.           Так           при

E = 2 , 1 ■ 10 6 кгс / см ² , ц = 0 , 33 , р g = 7 , 8 ^

chh v кр = I            1 — = 4 ■ 10 3, —, м/.

• 4 ^э (1 — ц2) U         RR/с

На рисунке 2 приведены зависимости для коэффициента динамичности от скорости движения нагрузки для трубы с внутренним диаметром d = 125 мм и различной толстостен-ностью lam=d/D. Из графиков следует, что коэффициент динамичности в значительной степени растет с увеличением lam, т.е. с уменьшением толщины стенки.

Коэффициент динамичности кольцевого давления оказывается значительно больше коэффициента динамичности внутреннего давления.    Например,    при    lam=0,75    и v = 1700 м/с имеем х = 0,61 имеем: kдр = 1,61 ;

w max

k дq

^q 8^1 —7

F—x

k_д p = 1 , 09 . Полученное Ильюшиным А.А., Огибаловым П.М. решение в виде выражений (1) для коэффициентов динамичности имеет общее важное значение, доказывающее наличие динамических эффектов в случае быстро-перемещающегося фронта нагрузки, а также частное практическое значение для тех импуль-

сных систем, к которым соответствует приня- тая система допущений.

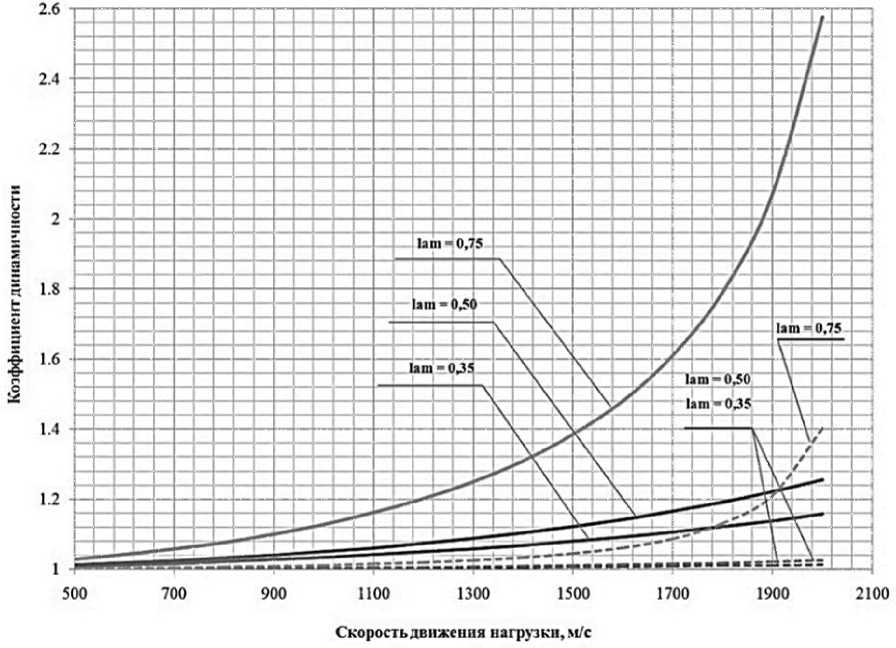
Рисунок 2 - Зависимость коэффициента динамичности от скорости движения нагрузки: сплошная линия – для кольцевого давления; штриховая линия – для внутреннего давления

Однако в большинстве практических задач проектирования необходимо учитывать как сложную геометрию устройства, т.е. переменное сечение стенок трубы, так и переменный характер нагрузки, а также изменение скорости ее переднего фронта [2].

Подобные задачи [3] можно решать на основании общих численных методов механики сплошной среды, реализованных в САЕ системах, например ANSYS/LS DYNA, с использованием решателя явного типа, дающего возможность проводить динамический анализ при нелинейности механической системы.

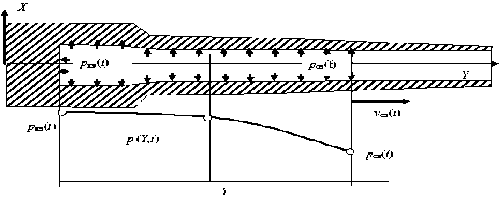
Рисунок 3 – Расчётная схема

В качестве примера рассмотрим осесимметричную конструкцию (рисунок 3) – трубу переменного сечения, закрытую с одного конца дном, в области которого формируется импульс нагружения, например, при сгорании топлива. Далее фронт импульса распространяется к открытому срезу трубы, а его скорость движения и величина нагрузки изменяются во времени. Причем нагрузка переменна по всей поверхности трубы и зависит от координаты в каждый момент времени нагружения.

Изменения нагрузки во времени и пространстве характеризуется трехмерной диаграммой в координатах ( Y, t, p ) , (рисунок 4). При построении указанной зависимости принималось, что давление на поверхность канала было переменным по его координате и в каждый момент времени определялось зависимостью:

f Y )

Р ( ^Y ,t ) = p кн ( t ) - [ p кн ( t ) - p c н ( t ^)] -| ---- Tri , ⁽²⁾

I 1сн (t )J где pKh(t) и pcH(t) - переменные во времени значения давлений у закрытого торца трубы и во фронте перемещающейся нагрузки, соответственно; 1 сн (t) - путь, пройденный фронтом импульса давления к моменту времени t от начальной точки y0 = Yfl - 1д ; 1д - полный путь, пройденный фронтом импульса давления; Yfl -координата открытого среза трубы.

Зависимость 1С„ (t) имеет нелинейный характер. В момент прохождения фронтом импульса соответствующего сечения канала, дав- ление на его поверхности будет возрастать практически скачком от атмосферного до значения давления топливных газов у фронта им- пульса в текущий момент.

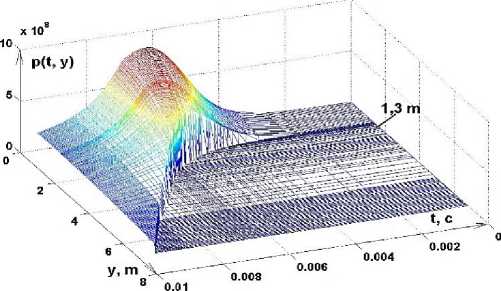
Рисунок 4 – Закон изменения давления, действующего на поверхность канала трубы

Как допущение принято, что возможные поперечные колебания трубы не оказывают существенного влияния на ее НДС и прочность. Принятая система допущений позволяет в целом привести задачу к осесимметричной.

Механические характеристики материала трубы принимались следующими: модуль упругости E = 2,1 ■ 1011 Па , коэффициент Пуас сона v = 0,333 , плотность р = 7950 кг/м3 .

При дискретизации расчетной области на элементы прочностного динамического анализа, необходимо определить наибольший размер элемента, который должен обеспечить динамическое решение задачи. В большинстве случаев принято [6] определять максимальный размер элемента как половину расстояния, ко- торое проходят упругие волны в материале за минимальный временной промежуток между дискретными значениями прикладываемой нагрузки.

Скорость распространения упругих волн в материале определяется формулой

E

с

^- ц ² ) ■ Р

где: E, ц и р - упругие константы и плотность материала. Тогда максимальный размер элемента l max

A t

5 тft

E

^- ц ² ) ■ Р

Установим наибольшую разность между дис- кретными значениями времени в расчетных вариантах A t = 2,3 ■ 10 5 с . Откуда максимальный размер элемента по формуле (4) равен lmax 5 0 ,0627 М .

Для реализации расчета необходимо ввести силовые и кинематические граничные условия задачи. Кинематически конечноэлементная модель не ограничивается. В качестве силовых граничных условий необходимо ввести давление на поверхности канала трубы. В препроцессоре такой ввод предусмотрен для групп узлов или конечных элементов. Однако ввести кривую нагружения для каждого элемента во времени не представляется возможным вследствие большого объема вводимых данных.

Закон изменения давления, действующего на поверхность канала устройства в пространстве координат ( Y, t, p ), представлен в виде трехмерной поверхности (рисунок 4). Соответственно, для каждой точки на внутренней поверхности с фиксированной координатой Y может быть получена кривая зависимости давления p только от времени p ( t )| y=const .

Для осесимметрической конечноэлементной модели конструкции нагрузочными элементами будут являться линии, определённые по двум соседним узлам, принадлежащим поверхности канала и одному и тому же элементу одновременно. Следует отметить, что для варианта с исходным разбиением геометрии на внутренней поверхности может находиться около тысячи элементов. Следовательно, необходимо подготовить столько же нагрузочных кривых и столько же нагрузочных записей.

Для сокращения требуемого времени на подготовку разработана программа в среде Delphi , вычисляющая для каждого элемента, принадлежащего поверхности канала устройства, нагрузочную кривую и формирующая нагрузочную запись. Нагрузочные кривые и записи формируются в виде двух файлов пригодных для передачи в решатель. Исходными данными для программы являются номера узлов, определенные из дискретизации расчетной области, данные о нагрузке и результаты работы препроцессора, содержащие координаты и номера узлов конечно-элементной сетки, а также номера элементов и принадлежащие им узлы.

Порядок действий по формированию нагрузочных кривых и записей следующий:

• 1    Вводятся номера узлов, находящихся на внутренней поверхности трубы.

• 2    Определяются номера элементов, которым принадлежат введенные узлы по данным содержащимся в файле filename.к , сформированном препроцессором.

• 3    Вычисляются координаты центра тяжести меридионального сечения элемента.

• 4    По осевой координате центра тяжести Y элемента формируется зависимость давления от времени с учетом расстояния, пройденного на текущий момент фронтом импульса.

• 5    Соответствующей нагрузочной кривой присваивается номер соответствующей нагрузочной записи.

• 6    Производится формирование файлов нагрузочных кривых и записей.

• 7    Сформированные файлы прикрепляются к файлу filename.к для дальнейшего расчёта.

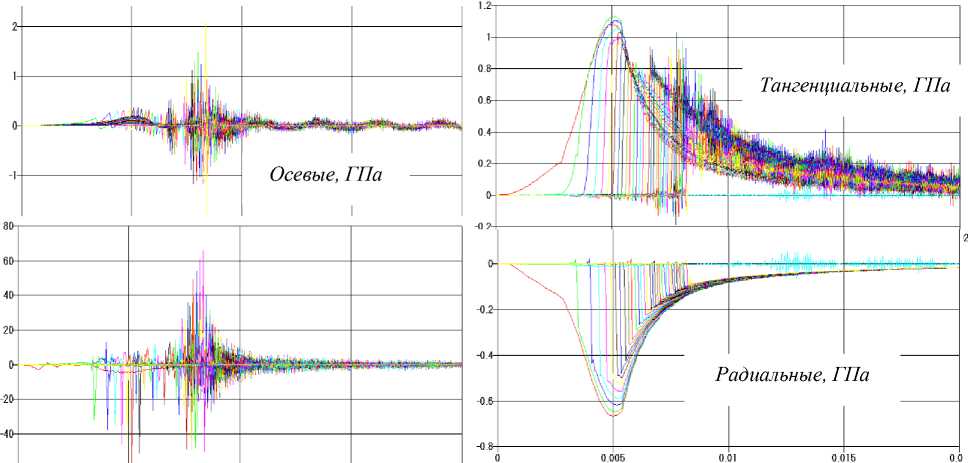
На рисунке 5 представлены графики зависимостей компонент тензора напряжений от времени для различных точек вблизи поверхности канала устройства, диаметром канала 125 мм и длиной 7,0 м. Из графиков следует, что после момента, соответствующего наибольше- му давлению, наибольшие напряжения сначала падают, а затем возрастают в точках, близких к открытому срезу трубы. На графиках наблюдаются выраженные пики напряжений в поперечных сечениях, близких к открытому срезу. Эти пики совпадают по времени с моментом прохождения фронтом данного сечения. Величина интенсивности напряжений определяется в основном колебаниями тангенциальных и осевых напряжений. В рассчитанном варианте пики интенсивностей напряжений превышают наибольшие значения напряжений, соответствующие моменту максимального давления.

О                     0.005                    0.01                    0 015                   0.02

tc

Рисунок 5 – Компоненты напряжений для внутренних точек трубы от времени в с

Расчеты НДС показывают наличие высокочастотного процесса деформирования стенок трубы. Эффекты динамичности воздействия нагрузки в полной мере реализуются в средней части и у открытого среза трубы.

Наличие запредельных напряжений а, обусловлено динамическим характером нагружения от быстро перемещающегося с переменным ускорением фронта нагрузки. Максимальные значения коэффициента динамичности k для таких случаев можно определить как отношение интенсивности напряжений при динамическом расчете а, к интенсивности напряже ний при статическом расчете а Ст :

2 r ₂

p • r i

2 r ₁

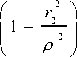
о

t

p • r i

2 r ₁

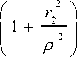
• r 2

а.      = p •.

t max            22

r 2

где r ,r2 и p - соответственно внутренний, наружный и текущий радиусы трубы в рассматриваемом сечении. При этом радиальное напряжение также наибольшее и, как следует из (5), равно а гтах = — p . Так как расчет стати- ческой прочности следует выполнять для наиболее нагруженных точек, то условие прочности по теории Треска записывается в виде:

k a

а .

i

.

ст а i

о

пр

о, tmax

—

о rmax

r + r2

Р • —2----г — (— p) = p • —22

F — r— r r2     r1                         r2

.

В первом приближении для статической оценки можно считать статические напряжения по формулам [4], характеризующим трубу, нагруженную внутренним давлением p :

Учитывая незначимую разницу между

условиями Треска и Мизеса для рассматриваемого случая можем принять приближенное ра-

венство:

ст

σ ≈σ i           пр

2 r

= p ⋅

2 r ₂

- r ₁

На рисунке 6 сопоставлены значения статических и динамических интенсивностей напряжений в точках их локальных максиму- мов.

Из рисунка 6 следует, что коэффициент динамичности имеет значения, в несколько раз превышающие единицу и возрастает к дульному срезу, где его значения имеют наибольшее значение по двум причинам. Первая обусловлена наибольшими динамическими напряжениями, а вторая – наименьшими статическими вследствие малой величины давления и дульного утолщения.

Основной вклад в значения интенсивностей напряжений вносят окружные и осевые напряжения. Причем последние, в основном, и обуславливают динамичность процесса. Сдвиговые напряжения имеют значения на один-два порядка меньше значений интенсивностей напряжений и не оказывают на них практического влияния.

Анализ графиков зависимости компонентов и интенсивности напряжений от времени для различных областей средней и дульной частей трубы показывает следующее:

• -    возбуждение колебаний компонентов σ , σ и интенсивности σ напряжений происходит до подхода фронта нагрузки к расчетному сечению;

• -    наибольшие значения компонентов

σ , σ и интенсивности σ напряжений достигаются в момент прохождения фронтом расчетного сечения;

• -    после прохождения фронтом нагрузки расчетного сечения происходит значительное снижение амплитуды значений компонентов σ , σ и интенсивности σ напряжений в рас-

• сматриваемых сечениях;

• -    после выхода фронта нагружения за открытый срез трубы амплитуда значений интенсивности напряжений в центральной части и у открытого среза трубы изменяется периодически и постепенно снижается;

• -    несущая частота колебаний находится в пределах 8-10 кГц, которая модулируется основными колебаниями частотой 380 Гц;

• -    расчетные значения коэффициентов динамичности достигают величины k = 2 и более.

В результате расчета динамических процессов, происходящих в трубах различной геометрии и характеризующихся различной формой нагружаемого импульса [6], установлено, что динамичность процесса, оцениваемая коэффициентами динамичности k в большой степени зависит от скорости распространения импульса, от крутизны его фронта (возрастает), от толщины стенки трубы (убывает) и от ее длины (возрастает).

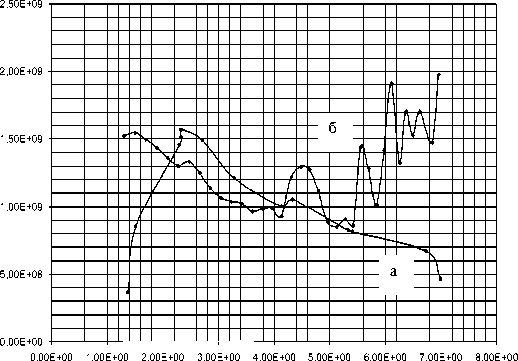
Рисунок 6 – Характер изменения огибающих напряжений по длине трубы : а) – в статических условиях, б) – в динамических условиях

Выводы:

• 1    Разработана методика расчета напряженно-деформированного состояния трубы с учетом динамичности воздействия нагрузки на базе специализированного пакета ANSYS/LS-DYNA , реализующая явный метод решения конечно-элементной модели.

• 2    Исследован характер изменения напряженного состояния труб, нагружаемых динамическим импульсом.