Определение доверительной области параметров траектории баллистического объекта по угловым измерениям

В работе рассматривается классическая задача определения параметров траектории баллистического объекта только по угловым измерениям из одного пункта наблюдения [1]. Такая задача возникает, например, при аварийном запуске искусственного спутника Земли, когда единственной информацией, по которой можно определить параметры движения ракетоносителя (или уже отделившегося от него космического аппарата), являются измерения угловых координат с помощью приёма сигналов телеметрии пассивным радиоинтерферометром или оптическим телескопом. Описывается алгоритм построения апостериорной плотности вероятности (в общем случае не гауссовской) вектора параметров траектории баллистического объекта, использующий предложенный в [2] точный метод решения кусочно-линейной задачи оценивания. Предлагается метод определения доверительной области координат точки падения объекта для случая, когда форма этой области существенно отличается от эллипсоидальной. Приводится пример условий наблюдения, при которых

действительная апостериорная плотность вероятности вектора параметров траектории движения существенно отличается от нормальной.

Далее принимаются следующие допущения.

• 2.    Модель движения баллистического объекта

Движение баллистического объекта подчиняется дифференциальному уравнению вто рого закона Ньютона:

Л =Ф(Z ),

правая часть которого определяется силами, воздействующими на объект (гравитации, аэродинамического сопротивления), а компонентами фазового вектора Z (т ) = [R, F, L,V,U, А]^т являются расстояние R = R (т ) объекта от центра Земли, его географические широта F = F (т ) и долгота L = L (т ), модуль скорости V = V (т), угол U = U (т ) наклона вектора скорости относительно текущего горизонта, азимут A = A (т) плоскости полёта (х^т~ транспонированный вектор х). При экстраполяции в точку падения в вектор состояния добавляется седьмая компонента: баллистический коэффициент для учёта торможения в атмосфере. При этом на диагональ ковариационной матрицы ошибок оценивания добавляется дисперсия ошибки, рассчитываемая на основе априорного интервала возможных значений баллистического коэффициента.

Фазовый вектор Z (т ), соответствующий некоторому произвольному моменту времени т, связан с начальным фазовым вектором Z (т о ) известным преобразованием «прогноза»:

Z, = Z (т t ) = Ф [Z (то) , т , - то] ,

которое основано на численном интегрировании уравнения (1).

На относительно коротком интервале наблюдения (т т — т1) можно пренебречь влиянием торможения в атмосфере и отличием от центральной модели гравитационного поля Земли на точность оценивания параметров движения. При этих допущениях по двум заданным в ЗН)-пространстве точкам (a i ,P i , d i ) и (а т , Р т ,d T ) можно построить единственную баллистическую траекторию, проходящую через эти точки в соответствующие моменты времени т 1 ,тт- Следовательно, фазовый вектор этой траектории например Z t = Z (т т )■ является функцией вектора X = [d i ,d T .a i ,P i ,a T , Р т ]^Т'-

Zt = Ф (Х).(3)

• 3.    Модель измерения

Для t = 1, ...,Т тонущий фазовый вектор Z t связан с текущими азимутом a t = а (т t ) н углом места fi t = P (т_t) объекта известными преобразованиями:

at = а (Zt), pt = Р (Zt).(4)

С учётом функции прогноза (2) в (4) угловые координаты можно представить как функцию конечного фазового вектора Zt'

at = а (ф[Zт,тt - тт]) = at (zt), pt = p (ф[Zт-Ft - тт]) = pt (zt) .(Д

Подстановка (3) в (5) даёт для t = 1,...,Т связь текущих угловых координат (a_t,p_t) объекта с параметром X:

at = at (Ф(Х)), Pt = Pt (Ф(Х)).(6)

Пусть a_t, p_t - измерения соответственно азимута a_t = а (т_t) и угла места p_t = P (т_t), t = 1, ...,Т. Обозначим:

N ,,m_H  Ta, (Ф(Х))1

- - ы    ' ^(Х)= ы = Ip, (Ф(Х))] ■

Принимается модель, в соответствии с которой измерение у , угловых координат a t ,/3 t является реализацией случайной величины

Y t = h t (X ) + e t ,

где, E i ,...,Ep - последовательность некоррелированных нормальных ошибок измерения с нулевыми средними и известными ковариационными матрицами Wt = Ме^,

Обозначения

Y = ' Y." • • • , у = у. ■ ■ ■ , h (X) = ' hi (X) • • • , e = ei ■ ■ ■ , W = diag {W1,...,Wт} . YT. . ут. .hт (X)_ .£т_ позволяют представить уравнение для объединённого вектора измерений Y в виде

Y = h (X ) + e.

(Ю)

Процедуры, реализующие функции (2), (3), (7), не являются предметом данной работы и используются как готовые инструменты.

4.    Оценка вектора состояния

Рассмотрим задачу построения оптимальной по некоторому критерию оценки ж параметра X на основе измерения у случайного вектора Y, а также определения ковариационной матрицы ошибок оценивания Г = Г (ж) = ( [ж (у) — ж] [ж (у) — х]Тру (у |ж )dy. В соответствии с (10) и принятыми допущениями функция правдоподобия ру (у |ж) = Ny {h (ж), W} является гауссовской со средним h (ж) и ковариационной матрицей W. Следовательно, максимально правдоподобная оценка ж находится из критерия J (ж) = minJ (ж), в котором X целевая функция имеет вид

т

J (ж) = [у - h (ж)]^тW^-1 [у — h (ж)] = ^ [y t — h t (ж)] ^т W -¹ [y t — h t (ж)],        (11)

t=i а ковариационная матрица ошибок оценивания приближённо считается совпадающей с обратной матрицей Фишера и вычисляется по формуле

Г=

( ^{dh (ж)} Д ^Т _W - I ^{dh (ж)}

у дж          дж

- i

( ^dh t ^(ж) )

М )

. t=i

т

Wt

i

dh t (ж) дж

i

Критерий максимального правдоподобия с целевой функцией (11) совпадает с обобщённым критерием наименьших квадратов, и, следовательно, в рассматриваемом случае оценка максимального правдоподобия совпадает с МНК оценкой.

4.1.    Итеративный метод наименьших квадратов

Для вычисления оценки ж вектора X из условия минимума критерия (11), а также соответствующей ковариационной матрицы ошибок оценивания Г используется итерационный метод наименьших квадратов [1,3,4], который, с учётом структуры (9) векторов у, h и матрицы W, можно представить в виде

^+1 =ж , + Г £ (^ : W ^-1 [у ,

— h t (X i)] ,

Г. . -У ( ^д5^ Щ( ^)] ¹

Итерации прекращаются, например, при выполнении условия \J (^+1) — J (Xi)\ < А, где А — желаемая точноств вычисления критерия (И). В качестве оценки ж и ковариа ционной матрицы ошибок оценивания Г принимаются величины Xi+i, ri+i, полученные на последней итерации. Итерационный процесс (13), (14) требует задания некоторого началь- ного приближения Хо, обеспечивающего сходимоств к точке минимума функции (И). В качестве началвного приближения для компоненты X2 = [ai,0i,aT,0т]Т вектора X в работе

= [а1,Л,атЛ] , а начальное приближение Xi = (d^ T ) d_T ]^Т задаётся в цикле перебора (с некоторым шагом) допу

исполвзуется измерение X2 для компоненты Xi = [di, стимых значений дальностей di,dT Для каждой фиксированной пары di,dT запускается итерационная процедура (13), (14). В качестве оптимальной выбирается оценка X, которая соответствует минимальному значению критерия (11).

4.2.    Итеративный метод наименьших квадратов с фиксированными дальностями di; dT

Для построения доверительной области точки падения объекта потребуется следующий алгоритм оценивания вектора X при фиксированном значении компоненты xi = ж* = [di,dT]T.

Обозначим

^X = [^X2] ■ ^X i = И ■ ^X

a₁ 0 1 a T _ ⁰t_

Г х0      Ы         Ь 1

^х = Ц , ^X1 = Ц , ^х 2 = а т

и представим целевую функцию (11) при фиксированном значении компоненты Xi = х* = [d 1 ,d T ] ^Т в виде функции компоненты X2 = [а 1 ,Ь 1 ,а т ,Ь т ]^Т:

J (х) = J (X 2 \х* ) = [у — h (x i , X 2 )] ^T W ⁱ [у — h (х*, X 2 )] .

Оценка д вектора X2 по измерениям y i , ...,у т при условии Xi = х* вместе с соответствующей ковариационной матрицей ошибок оценивания у могут быть вычислены с помощью итеративного метода наименьших квадратов:

Дi +i = Д i + У ^( ^dht fa^ ) ^Wt ^{i [}У* ^{— ht} (^ д^{0 0}            (¹⁷)

• - = g (^)Vⁱ (№4)] \      ₍₁₈₎

4.3.    Редуцированная целевая функция 4.4.    Пример моделирования итерационного МНК

стартующего с начальным условием до = [ai, 0i , а т ,0 т ] • После остановки процесса итераций в качестве оценки д и ковариационной матрицы ошибок оценивания у принимаются величины M i+i и yi+i, полученные на последней итерации. Поскольку для начального приближения используется непосредственное измерение a_i,0_i,a_T ,0_Т угловых координат а±,0±,а т ,0т, итерационный процесс (17), (18) сходится, как правило, за одну итерацию.

Пусть для любого фиксированного значения Xi с помощью алгоритма (17), (18) определена оценка д = д ( x i ) компоненты X2, а также соответствующая ковариационная матрица ошибок оценивания у = у (xi). Критерий оптимальности (16) можно представить как функцию компоненты Xi:

J d (x i ) = J (х-тд (x i )) = [у — h (х-тд (x i ))]^TW^-i [у — h (х^д (x i ))] .         (19)

Таким образом, решение задачи определения оптимальной в смысле критерия (11) оценки сводится к задаче поиска минимума редуцированной целевой функции (19) по ж1 в двумерном пространстве.

Все приведённые в работе примеры получены для траектории баллистического объекта, падающего на поверхность Земли под финальным углом к горизонту 30° со скоростью 7 км/с. Измерения азимута и угла места проводятся с периодом 5 с со среднеквадратической ошибкой 1.0 угловая минута, начиная с дальности от измерителя до объекта 3000 км.

На рисунке 1 показан результат моделирования работы алгоритма (13), (14). Ось абсцисс соответствует координате Д, ось ординат - координате dp. Показаны действительная пара дальностей d i ,dp', начальные значения, из которых итерационный МНК успешно сошёлся; точка (в данном примере единственная), куда сошёлся МНК. Эллипс ограничивает классический доверительный эллипсоид, содержащий истинные значения d i ,d p с вероятностью 0.9. Рельеф целевой функции (19) в зависимости от значений дальностей d i ,d p представлен в виде изображения карты высот в оттенках серого. Каждый пиксель изображения представляет значение целевой функции, цвет «0» (чёрный) соответствует самой низкой точке, а цвет «255» (белый) — самой высокой. Область рисунка, где рельеф целевой функции не отображён, соответствует физически недопустимым дальностям. Из рисунка видно, что имеется обширная область значений дальностей d i ,dp, из которых МНК не сходится к минимуму целевой функции.

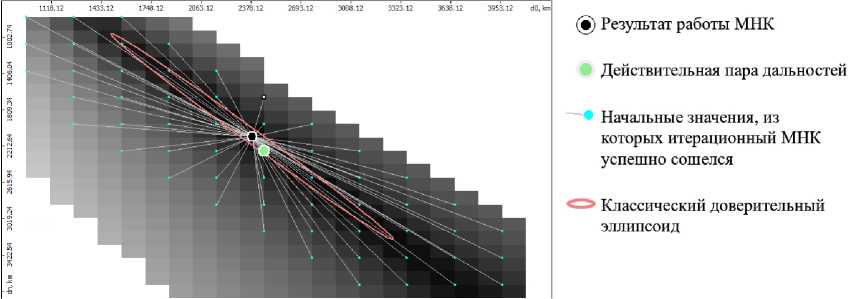
Рис. 1. Сходимость итерационного МНК из разных начальных точек (наблюдение в течение 100 с)

4.5.    О точности оценивания

Для произвольной нелинейной функции h (ж) в (10) оценка максимального правдоподобия не является эффективной, её ковариационная матрица ошибок оценивания не совпадает с обратной матрицей Фишера и, вообще говоря, получить для неё точную формулу не удаётся. Если параметр X интерпретировать как случайный, то при использовании равномерной на области П С E k априорной плотности вероятности р х (ж) = 7q (ж)/V в пределе при П ^ Ek с помощью байесовского соотношения можно получить следующую формулу для апостериорной плотности вероятности:

Р х |Y ^(ж [У ) = P Y |х ⁽У ^|ж )/1 P Y |х ⁽У ^{|ж )dж} .                         (20)

Е _к

Таким образом, при равномерной на Ek априорной плотности вероятности случайного параметра X его апостериорная плотность вероятности с точностью до нормирующего коэффициента совпадает с функцией правдоподобия, следовательно, arg maxpy|х (у |ж) = arg maxpx|Y (ж |у),                       (21)

Ж                        X т.е. оценка максимального правдоподобия совпадает с байесовской оценкой при простой функции потерь (т.е. с точкой максимума апостериорной плотности вероятности).

В этом смысле модель равномерного на всем E k априорного распределения параметра может быть использована в ситуации отсутствия априорных данных о параметре. Далее будем считать, что параметр X носит случайный характер и имеет равномерное на E k априорное распределение. Если для апостериорной плотности вероятности приемлема гауссовская аппроксимация

P x i y (ж \у ) ~ Х_х {х, ^г} ,                                  (22)

параметры х, Г которой определяются с помощью алгоритма (13), (14), то точность оценивания полностью характеризуется ковариационной матрицей ошибок оценивания Г. При этом доверительная область D, содержащая параметр X с требуемой вероятностью Р и = Р {X G D \Y = у } и удовлетворяющая соотношению

У Р х | y ^(х \у ) dx = ^р с ,                               (23)

D является эллипсоидом

D = |х G E_k |(х - х)^тГ^-1 (х - х) < с² } ,                      (24)

для которого величина константы с выбирается в зависимости от требуемой величины доверительной вероятности Рс- Аппроксимация (22) корректна, когда якобиан ^дул) ^ПР^И вариации х в пределах основной «массы» апостериорной плотности N_x {х, Г} изменяется незначительно. В общем случае следует проверять допустимость использования матрицы Г и доверительного эллипсоида (24) для характеризации точности оценки х. В предлагаемой работе допустимость приближения (22) для рассматриваемой прикладной задачи проверяется с помощью построения асимптотически точной аппроксимации действительной р х | y (х |у) кусочно-гауссовской плотностью вероятности, параметры которой определяются с помощью метода, предложенного в [2] и основанного на точном решении задачи оценивания параметра X для случая, когда функция h (х) в уравнении наблюдения (10) кусочно-линейная.

• 5.    Кусочно-линейная аппроксимация нелинейности

  [X2]

  
  

Пусть a priori компоненты Xi = [di,dT ]Т и X2 = [_aij3i, ат ,^т]Т пара метра X = статистически независимы и имеют равномерные на ограниченных областях Q1 С E2 и

^2 С E4 априорные плотности вероятности:

Р Х 1 (х 1 ) =        , V 1 = / dX 1 , Р Х 2 (х 2 ) = ¹^ 2 1 , V 2 = / dX 2 .

у1

Ω1

Таким образом, априорная плотность вероятности параметра X имеет вид

Рх (х) = -V^)!, у = У1 XV2, Q = {х1 G E2^2 G E4 \х1 G П1,х2 G Q2 } .(26)

Далее будет рассмотрен асимптотический случай Q2 ^ E4.

Компонента X2 измеряется непосредственно. Будем считать, что точность её измерений достаточно высокая для того, чтобы считать функцию h (х) = h (х1, х2) практически линейной по х2 па апостериорной доверительной области 'значений параметра X2. С другой стороны, компонента X1 непосредственно не измеряется и при вариации х1 в пределах области Q1 якобиан ^(д^ = ^(д¹,^²) может, в принципе, существенно изменяться.

Разобьём Q i на совокупность непересекающихся областей Q i = O 1U ... U И” таких, что при изменении xi в пределах каждой из них нелинейностью функции h (x i ,x 2 ) п⁰ xi,x2 можно пренебречь. Воспользуемся кусочно-линейной аппроксимацией

п h (x) = 52^ (x)(bi + B-x)                          (27)

i=1

в которой

Q i = {x i G E 2 ,X 2 G E 4 \ x i G Q 1 ,X 2 G Q2 } , B -

dh (x)

где х - = (хфц (xi)), xi — геометрический центр области Qi, а ц (xi) - оценка компоненты X 2 с помотцью алгоритма. (17). (18) с фиксированными дальностями x i = x i-

Применяя аппроксимацию (27), представим уравнение наблюдений (10) в виде

п

Y = ^ I q , (X) (b i + B i X )+ е. i =i

• 6.    Кусочно-гауссовская апостериорная плотность вероятности

Покажем, что в принятых допущениях апостериорная плотность вероятности параметра X имеет кусочно-гауссовский вид

PXIY (x \У) = ^ Iq, (x) ViNx {xi, Г-}/^ r-P- ,(30)

i=i где

Pi = J N {x-, r{}dx,(31)

Q i

Ri = [y — bi + Bix]TW-i [y — bi + Bix] ,(32)

xi = x+ BTW-iB-)-iBTW-i [y — bi + Bix] ,(33)

г- = (bTw-iBi)-\(34)

ri = exp {a — Cmax} , c- = 2 (ln |Г-| — R), Cmax = max {a} .(35)

Действительно, пусть Q - ограниченная область с конечным объёмом V и равномерная на. Q априорная плотность вероятности параметра X имеет вил

Px (x) = Iq (x)/V .(36)

В соответствии с уравнением (29) функция правдоподобия p y | x ( у |x) вычисляется по формуле

PY|X (у |x) = ^ iQi (x)Ny {bi + Bix, W} .(37)

i =i

Подстановка (36), (37) в формулу Байеса

Px|Y (x |У) = Py|x (У |x) Px (x)/ / Py|x (У |x) Px (x)dx даёт п                                  П „

P X I Y (ж [у ) = ^ I ^ i (ж) N y {b i + B i x,W}/^J ^N y {b i + B i X,W } dx .       (38)

Заметим, что фигурирующий в (36) объём V области И сократился в числителе и знаменателе формулы (38), и поэтому формула (38) остаётся в силе в асимптотическом случае при И ^ Е2.

Восполвзуемся тождеством

N y {b i + B i X, W } = (/^T Nn N y {b i + B i X i , W } N x {X i , Ti} ,          (39)

в котором параметры     X i , Ti    определены формулами

(33),      (34)

ПЛОТНОСТИ при подста-

и которое следует из формулы для нормальной

N y {b i + B i X,W } = -^Х^ • exp |-2 (у - b i - B i x)^T W ^-1 (у - b i - B i x)} новке в неё тождества

(у - b i - B i x')^TW ^-1 (у - b i - B i x) =

= (у - b i - B i X i ) ^T W ¹ (у - b i - B i X i ) + (X i - x)^T r_i¹ (Xi - x) .

Подстановка (39) в (38) даёт f 1ъ(x) , I N {bi + BiXi, W} Nx {Xi, Ti}

PXIY (x |у ) = ^=П-------------------------------------------------.( f ^FjNy {bi + Bi Xi, W} / Nx {Xi, Ti} dx i=1Q

Применяя обозначение (32), можно воспользоваться представлением

N y {b i + B i X i , W } =       ¹     _: exp j -¹ B i I .

VЫ |W|

Подстановка (41) в (40) приводит к формуле п          ___

P x |Y ^(x |у) =

f hi (x)У)г)[exp {-2 R i} N x {X i , Pi} i=1

12 VlTT exp {-2 R i } J N x {X i , Ti} dx i=1                       Q _i

Разделим числитель и знаменатель (42) на dk = у/ |Гк| exp {-| Rk}, где номер k выбирается из соотношения C k = max {ci, ...,с_п }, в котором C i = ln d i = 2 (|ri| - Ri), и представим

△ xi =

d=exp{ln t}

= exp {ln d_i - In d k } = exp {c_i - C k } .

В результате с учётом обозначений (31) - (35) из (42) следует (30).

7.    Апостериорная плотность вероятности оцениваемых дальностей

Рассмотрим случайный вектор X с нормальной плотностью вероятности

P x (x)

X i , ri:

Nx {Xi, ri}. Аналогично (15) представим в блочном виде параметры X, х=й ■=Й] ■r=

Г'и  Щ

(ПУ Г2,2

.

В соответствии с теоремой о нормальной корреляции [5]

Р%2|Х1 ^(х2 ^IX 1 ) = N_X 2 {p i (жД ,^^} ,                              (45)

	P i (хД = х2 + r2,i (г1,1) 1 (х1 - х1) ,                            (46) 7i =Г2,2 - П,»->2,1 ) Т .                      (47)
С учётом (45):	Nx {X i , ri} = Nx 2 {p i (х1), 7i} Nx1 {х1, >} .                      (48)

Подстановка (48) в (30) даёт в асимптотическом случае Q2 ^ Е 2 совместную апостериорную плотность вероятности компонентов Х 1 ,Х 2 пара метра X:

пп

РХ1,Х2Х (х1,х2 \у) = ^Tqi (х1) Xi nX2 {Hi (X1) ,yj NX1 {x{, г\1}/^г{1>{ .(49)

i=1

В частности, из (49) следует формула для апостериорной плотности вероятности компоненты Xi: пп

РХ1|У (х1 \у) = ^ %1 (xi) XiNxi {X1, г1,1}/^ XiPi .(50)

i=1i=1

Действительно,

,. пп

РХ1|У ^(х1 \у )=            ^(х1) ^X i ^N X 2 {P i ^(х 1 ) ,7i^{} N} X 1 {^х1, ^Г1,1 }^dx2^/£^Xi^Pi ,

Е4 i=1

откуда следует (50).

8.    Доверительная область оцениваемых дальностей

Проведём дополнительное разбиение каждой области Q} на непересекающиеся подобласти Q1,^fc, к = 1,...,К. Воспользуемся формулой (50) для определения апостериорной вероятности принадлежности параметра области Q1,^k:

^X i,k — ^X i

o i ^k

Nx1 {х1, Г1,1} <'х  >  X i P i .

i=1

Упорядочим величины n^ k ,i = 1,...,п, к = 1,...,К в порядке убывания и в этом же порядке упорядочим области Q}^k. Составим область D из областей Q}^k, включая их в D последовательно (в упорядоченном порядке) до тех пор, пока сумма соответствующих этим областям величин X i^ не превысит желаемую доверительную вероятность Pc- В силу способа построения область D является областью минимального объёма (в классе областей, составленных из Q}^k), которая содержит X с требуемой доверительной вероятностью.

На рисунке 2 представлен пример доверительной области дальностей (d i ,d T ), рассчитанной по формуле (50) для кусочно-гауссовской апостериорной плотности вероятности (50), и классического доверительного эллипсоида.

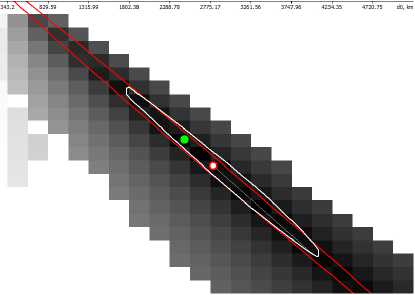
Рисунок 3 получен при большом времени наблюдения, при котором апостериорная плотность вероятности действительно близка к нормальной, и поэтому классический доверительный эллипсоид с большой точностью совпадает с доверительной областью. Рисунок 3 получен для непродолжительного времени наблюдения, при котором классический доверительный эллипсоид имеет заметно больший продольный размер, чем доверительная область, рассчитанная для кусочно-гауссовской плотности вероятности (30) и захватывает область физически нереализуемых пар дальностей (северо-западный участок рисунка). Для определения эмпирической вероятности попадания истинной пары оцениваемых дальностей в доверительные области было проведено 105 модельных экспериментов. При этом в белую областв истинная пара (di,dT) действителвно попала в 99% опытов. На обоих рисунках, как это и должно быть, максимум кусочно-гауссовской апостериорной плотности вероятности дал ту же оценку далвностей (di,dT), что и метод максималвного правдоподобия.

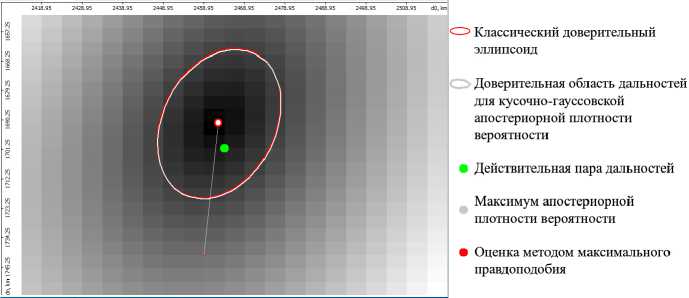
Рис. 2. Доверительные области дальностей (d 1 , df ) при времени наблюдеиия 350 с и Рс = 0.9

о Классический доверительный эллипсоид

С Доверительная область дальностей для кусочно-гауссовской апостериорной плотности вероятности

• •    Действительная пара дальностей

Максимум апостериорной плотности вероятности

• •    Оценка методом максимального правдоподобия

9.    Определение доверительной области координат точки падения 9.1.    Метод линеаризации функции прогноза

Рис. 3. Доверительные области дальностей (d 1 ,df ) при времени наблюдения 80 с

Рассмотрим вектор 0 = \F g , L g ]^Т, компонентами которого являются неизвестные географические широта F g, дол гота L g падения объекта на поверхноств Земли. Вектор 0 связан с X определённым преобразованием:

0 = ^ (X ).

Зная апостериорную плотность вероятности р х у (^х \У ) вектора X, требуется определить доверительную область Q С Е2, которой принадлежит вектор 0 с требуемой вероятностью Рс-

Классический метод [4] предполагает, что приемлемой является гауссовская аппроксимация рх\у (х \у ) ~ Ех {X, Г} апостериорной плотности вероятности вектора состояния с параметрами X, Г, вычисляемыми с помощью алгоритма (13), (14), а также допустимость линеаризации относительно оценки X нелинейного преобразования (52) прогноза вектора X в точку падения. В этом случае плотность распределения вектора в также можно считать нормальной ро (Р) ^ N^ {ц, у} с параметрами

Р = р (ж), Г о =

( ^дР (ж) Л _rf др (ж) V дж       дж

При этом в силу квазилинейности задачи оценка Р является квазиоптимальной (в смысле критерия наименьших квадратов) оценкой вектора координат точки падения в, а Го -апостериорной ковариационной матрицей ошибок оценивания. В таком приближении доверительная область вектора в является эллипсоидом и удовлетворяет неравенству

D o = У е E k

( р - р) Г о ¹ ( р - Р) < _су ,

для которого величина константы с^ выбирается в зависимости от требуемой величины доверительной вероятности Р и = Р {в е D o \Y = у }.

9.2.    Декомпозиция отображения доверительной области вектора состояния в доверительную область координат точки падения

Пусть определена апостериорная плотность вероятности р х |у (ж |у) вектора состояния X, а также доверительная область Di для компоненты Ji вектора состояния X = ^1 , соответствующая условию

^X 2

I РХ1|У (ж1 |у) Аж1 = Рс)(55)

D 1

Определим при любом фиксированном значении X1 = ж1 область D2 (ж1) условием у PX2IX1 ,у (ж2 |ж1,у)Аж2 = Рс2(55)

^ 2 ( Ж 1 )

Тогда вероятность Р попадания вектора X в область

D = {ж tEk|ж1 еD1,Ж2 eD2 (ж1)}(57)

определяется по формуле

Р = I Рх1У (ж |у) Аж = У I У Рх1,х2|у (ж1,ж2 |у )dж2 I dж1 =(58)

D              D1 ^(ц))

= У I У Р Х 2 | Х 1 ,У ^(ж 2 ^|ж 1 ,у ^)Аж 2 I Р Х 1 | У ^(ж 1 |у ^)Аж 1 .

p1 \Р2(Ж1)/

Подстановка (56), а затем (55) в (58) даёт Р = Р^^Р^) При выборе Р = Рс, Р^ = Рс2 (1)        (2).

получаем РС = РС = Р^с- Р = Рс Таким ооразом. из (об) следует \ Рх|у (ж |у) Аж = Рс-p что говорит о том, что определённая условием (57) область D содержит вектор X с вероятностью Рс и в этом смысле может рассматриваться как доверительная область, соответствующая доверительной вероятности Рс- Следует, однако, отметить, что построенная таким образом область D не является областью минимального объёма в классе областей, содержащих X с вероятностью Рс-

Поскольку имеется непосредственное измерение x2 = ^ai,Pi,aT, Рт] компоненты X2 = [a i , Р 1 ,а т , Р т ] ^Т, ^то её апостериорная плотность вероятности P x₂ i x 1 ,Y (x 2 \x i ,y ) при фиксированном значении компоненты Xi = xi может быть аппроксимирована нормальной плотностью вероятности px₂|x1 ,Y (x₂ \^Х 1 ,У ) = N_x 2 {р (xp ,7}, ^в которой параметры р (xi) ,7 вычисляются в соответствии с алгоритмом (17), (18).

Таким образом, экстраполяция доверительной области вектора состояния X в доверительную область точки падения может быть проведена следующим образом.

• 1)    Определяется доверительная область Di компоненты Xi по уровню доверительной вероятности рф. Это может быть либо эллипсоид, построенный в случае нормальной апостериорной плотности вероятности, либо доверительная область, построенная для кусочно-гауссовской апостериорной плотности вероятности описанным выше методом аппроксимации нелинейной функции h (x) в (10) кусочно-линейной поверхностью.

  
  
  
  

При обходе с некоторым шагом точек xi = хД, г = 1, ...,N границы области Di для каждого х^ в соответствии с (17), (18) определяются параметры p i = р (x^)) ,7^ плотности вероятности p_x2|_x1 ,_Y ^2 ^^, у^ = N_x 2 {p i ,7 i }.

В пренебрежении изменением якобиана J g (х 2 \xi) = ^щЦщ²) преобразования (52) при фиксированном значении x_i = x^ и вариации x₂ в пределах области, в которой сосредоточена основная «масса» плотности N_x 2 {p_i,7_i}, случайнь 1й вектор 0 = р (X_i,X₂) при фиксированном значении Xi = xiⁱ⁾ имеет плотность вероятности:

P e i X i (^P |^x i ^i}) = ^N a pi, 7,?} ,

где

P i = P

( _P (x ( i ) ) ) ’ 7 , ⁱ⁾ = ^J (p i |^x i ⁱ⁾) 7 i [^J , (p i |^x i ⁱ⁾)] .

. ( i )

Плотность вероятности (59) позволяет построить область D^, содержащую коорди- ( i ) паты 0 точки падения с вероятностью рРс при фиксированных дальностях Xi = xi^;.

( i )

Эллипсоиды Dg , г = 1,...,N ограничивают область Dg, которая содержит вектор 0 координат точки падения с вероятностью Р с (см. рис. 4). Аналогично можно определить доверительный интервал момента Т д времени падения.

9.3.    Метод виртуальных частиц

Метод виртуальных частиц [6,7] состоит в генерации облака виртуальных векторов состояния (частиц) x i Е D, г = 1,..., N в соответствии с плотностью вероятности P x i y (x \у ) и их преобразовании по формуле P i = р (x i ) в облако точек Pi, г = 1,..., N, которое образует «точечный портрет» доверительной области D g с весом каждой точки, соответствующим плотности p x | y (x \у )• Достоинством данного метода является его применимость в общем случае, когда плотность px|Y (x \у ) существенно отличается от нормальной и функция прогноза р (x) в (52) существенно нелинейная, а также отсутствие необходимости вычислительно ёмкого определения якобиана преобразования (52). Недостатком метода является необходимость использования большого числа виртуальных частиц для того, чтобы получить представительный (особенно на краях области при высоком уровне доверительной вероятности) «точечный портрет» доверительной области Dg. В предлагаемой работе метод виртуальных частиц применяется для тестирования и валидации предлагаемых алгоритмов построения области Dg.

9.4.    Пример расчёта доверительной области точки падения

На рисунке 4 показан пример доверительной области (по уровню Р с = 0.9) географических координат точки падения, рассчитанной следующими четырьмя способами:

• 1)    Построение классического эллипсоида рассеяния методом линеаризации функции прогноза.

• 2)    Декомпозиция отображения доверительной области нормальной апостериорной плотности вероятности N_x {х, Г} вектора X в доверительную область точки падения (эта (i)

область ограничена множеством эллипсоидов D ^ г = 1, ...,N).

• 3)    Декомпозиция отображения доверительной области кусочно-гауссовской апостериорной плотности вероятности вектора X в доверительную область точки падения (эта (i)

область ограничена множеством эллипсоидов D ^ г = 1, ...,N).

• 4)    Метод виртуальных частиц, заполняющих классический 6D доверительный эллипсоид, построенный для нормальной апостериорной плотности вероятности N_x {х, Г} вектора X.

10.    Заключение

Из рисунка 4 видно, что для приведённого примера классический эллипсоид рассеяния точки падения, полученный методом 1, не совпадает с точечным портретом, полученным методом 4. Следовательно, применение классического метода линеаризации функции прогноза для расчёта доверительной области точки падения, вообще говоря, является некорректным. В то же время можно видеть совпадение указанного точечного портрета с доверительной областью точки падения, полученной с помощью метода 2. Однако, в силу того, что для данного примера действительная апостериорная плотность вероятности вектора X отличается от нормальной, действительная доверительная область, рассчитанная методом 3, отличается от областей, полученных методами 1,2,4.

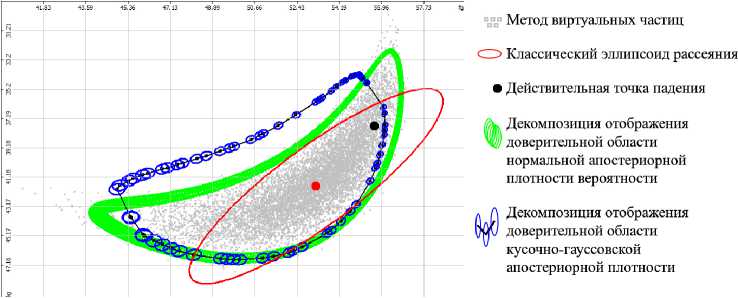
Рис. 4. Доверительная область координат точки падения, СКО ошибок измерения 10 [угл.мип.]

Итак, в работе получены следующие результаты.

Рассмотрена задача определения параметров траектории баллистического объекта только по угловым измерениям из одного пункта наблюдения для условий, когда линеаризация нелинейной функции, связывающей оцениваемый вектор параметров с измерениями, приводит к неприемлемым результатам.

Предложен алгоритм построения действительной апостериорной плотности вероятности вектора параметров траектории баллистического объекта, использующий кусочнолинейную аппроксимацию нелинейного уравнения канала измерений и построения кусочногауссовской апостериорной плотности вероятности. Предложен алгоритм построения дове- рительной области координат точки падения для случая, когда форма этой области существенно отличается от эллипсоидальной. Для условий наблюдения, при которых отчётливо проявляются нелинейные свойства рассматриваемой задачи оценивания, приводятся результаты моделирования предложенных алгоритмов и проводится их сравнение с результатами моделирования соответствующих классических алгоритмов.