Определение физико-механических характеристик материалов при исследовании концентрации напряжений в образцах с отверстиями

Определение физико-механических характеристик материалов до сих пор остается актуальной задачей проблем прочности конструкций. Иногда, экспериментальные данные можно использовать в качестве законов физико-механического поведения материала, вместо обычно используемого закона Гука.

Существуют стандартизированные методики измерения этих характеристик, однако вопросы измерений, универсальности, простоты и доступности, а. также неразрушающих методов контроля заставляют совершенствовать эти методики.

Наибольшими преимуществами обладают бесконтактные оптические методы. Известен интерферометрический метод определения коэффициента. Пуассона, материала, по нормальным изгибным компонентам перемещений при чистом изгибе образца. [1-3]. Методы голографической интерферометрии позволяют определить физико-механические характеристики при простейших испытаниях материала. [1, 2, 3, 5, 7].

Голографическая спекл-интерферометрия позволяет использовать образцы с диффузно отражающими поверхностями, существенно расширяя тем самым область исследуемых материалов. Предложена новая методика определения физико-механических характеристик материалов с использованием спекл-голографической интерферометрии натурных авиаконструкций. Метод спекл-голографии позволяет исследовать напряженно-деформированное состояние элементов авиационных конструкций из различных материалов [5-8]. Это позволяет определять физико-механические характеристики материалов при

«Московский физико-технический институт (государственный университет)», 2018

натурных испытаниях авиаконструкций. Технические константы материалов можно получить по интерференционным полосам, представляющим собой геометрическое место точек равного уровня перемещений при деформировании.

В голографической интерферометрии деформированных объектов чувствительность интерференционных полос существенно отличается по разным компонентам тензора деформаций. Поэтому при ограниченной корреляции оптических полей регистрации деформаций обычно наблюдаются главные компоненты тензора деформаций. Так, при растяжении достаточно толстых образцов наблюдаются плоские компоненты на интерферограммах, а при растяжении тонких образцов наблюдаются изгибные из плоскости деформации.

• 2.    Регистрация спекл-интерферограмм обрацов на промышленных испытательных машинах

Голографическая интерферометрия позволяет регистрировать напряженно-деформированное состояние на этапах нагружения вплоть до разрушения. В данной работе были проведены исследования по применению голографических методов для регистрации напряженно-деформированного состояния образцов на испытательной машине INSTRON Е 10 000 (рис. 1) при двух состояниях нагружения.

Рис. 1. Фотография экспериментальной установки:

1 - спекл-голограмма, 2 - образец, 3 - захваты испытательной машины

Методика внестендовой регистрации голограмм при испытании натурных образцов и элементов конструкций [5] позволила применить спекл-интерферометрию на испытательных машинах. При регистрации спекл-интерферограмм высокоразрешающие для голографии фотографические пластинки (ПФГ-ОЗм) жестко крепятся на образце на испытательной мащине. Полупроводниковый лазерный модуль также жестко располагался на жесткой раме. Расстояние от лазера до образца зависит от расширительной системы лазера. Падающая волна от лазера интерферирует с диффузно-отраженной волной от объекта в поле регистрирующей фотопластинки. Таким образом, фотопластинка регистрирует мик-роинтерференционную картину во встречных пучках - спекл-голограмму.

Метод двойной экспозиции состоит в записи на одну голограмму двух волновых полей, рассеянных объектом в двух последовательных состояниях, и наблюдении интерференционной картины этих полей при расшифровке. При получении картины полос - интерферограмм расстояние между интерференционными полосами, как правило, связано с длиной волны используемого излучения и деформациями объекта.

Регистрируя на одну и ту же фотопластинку два состояния объекта без изменения и смещения оптической схемы во встречных пучках, одно - на промежуточной нагрузке, другое - после приращения ХР на нагрузке при соответствующем дифференциальном нагружении, получаются спекл-голограммы двойной экспозиции сравниваемых двух состояний образца при растяжении [4, 5, 8].

Расчетное напряжение определяется по формуле:

д, =

где Д, - напряжение, ДР - дифференциальная нагрузка, S - площадь поперечного сечения образца.

Расшифровка спекл-голограмм двойной экспозиции производилась на оптической установке методом пространственной фильтрации.

• 3.    Метод пространственной фильтрации спекл-голограмм

Метод пространственной фильтрации спекл-голограмм является удобным и точным методом анализа и определения деформаций [6]. На тонких образцах присутствуют изгибные компоненты из плоскости, наблюдаемые вблизи нормального освещения, спекл-голограммы двойной экспозиции. На толстых образцах выделяются плоские компоненты деформации методом оптической фильтрации (рис. 2). С помощью этой методики получаем изображение интерферограмм с ценой полосы на интерферограмме, указанной ниже.

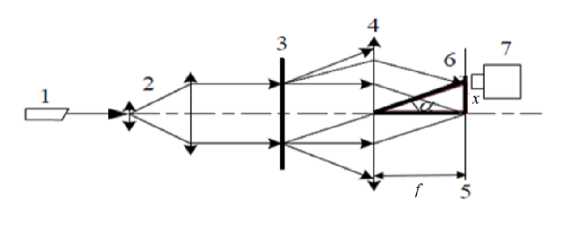
Рис. 2. Оптическая схема, фильтрации спекл-голограмм:

1 - лазер, 2 - коллиматор, 3 - спекл-голограмма, 4 - линза, преобразования Фурье, 5 - частотная плоскость, 6 - диафрагма, фильтрации пространственной частоты, 7 - видеорегистратор

sin a = tga =

ж

7’

U_x =

А

’ sin a

где U \ ^ цена полосы на интерферограмме, А - длина волны, 7 ^- фокусное расстояние объектива, sin a = tga на малых углах фтльтрации пространственных частот.

• 4.    Результаты испытаний для толстого образца

  На толстом образце из материала. Д-16 с размерами: толщина. 5 мм, ширина. 24 мм, с площадью поперечного сечения F = 120 мм², дифференциальная нагрузка составляла ДР = 100 — 400 кг, размер фотопластинок ПФГ 03м 50 х 50 мм², регистрировали спекл-голограммы. На рис. 3 представлена, оптическая схема, расшифровки спекл-голограмм по полосам Юнга. В результате расшифровки мы получили дифференциальную деформацию е = 0.37 • 10^-3 , что соответствует модулю Е = 6.8000 • 104 МПа Юнга. Оценка погрешности измерений составляет 5-10%.

На рис. 4 представлена, отфильтрованная спекл-интерферограмма, с ценой полос U \ = 2.4 мкм.

По нашим измерениям: результаты для толстого образца - деформация е = 0.35 • 10-3, модуль упругости Е = 7.1400 • 104 МПа. Полученные результаты измерения модуля упругости отличаются от табличных данных для алюминиевых сплавов Е = (7 — 7.2) • 104 МПа.

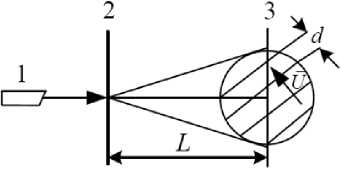
Рис. 3. Расшифровка, спекл-голограмм по полосам Юнга:

1 - лазер, 2 - спекл-голограмма, 3 - экран с полосами Юнга

Рис. 4. Отфильтрованная спекл-интерферограмма, а - шаг полос

• 5.    Результаты испытания тонкого образца. Интерферометрический метод определения коэффициента Пуассона материала по нормальным изгибным компонентам перемещений при растяжении тонкого образца

На тонком образце из материала. Д-16 с размерами: толщина. 2 мм, ширина. 60 мм, с площадью поперечного сечения Ғ = 120 мм², дифференциальная нагрузка составляла △ Р = 100 — 500 кг, размер спекл-голограмм 50 х 50 мм², регистрировали зону деформаций вблизи специального отверстия. При этом наблюдался изгиб поверхности тонкого образца, на. интерферограммах.

При изгибе поверхности конструкции эти полосы представляют геометрическое место точек равного прогиба, образующих семейство гипербол, угол между асимптотами к которым определяется величиной коэффициента. Пуассона, материала. Модуль упругости Юнга, можно определить как отношение напряжения к продольной деформации, линейно связанной с кривизной функции прогибов [1]. Модуль сдвига, определяется через модуль Юнга, и коэффициент Пуассона.

На тонких образцах присутствуют изгибные компоненты из плоскости. Главные компоненты деформаций при растяжении в плоскости выделяются методом оптической фильтрации [5]. Изгибная компонента ш регистрируется при наблюдении вблизи нормали к поверхности.

В прикладной теории упругости изгиба, пластин есть уравнение :

"< д2ш— ^^ш )= М:

0X2    оу2

где D - изгибная жесткость пластины, М - изгибающий момент.

При изгибе пластинки ее поверхность приобретает трехмерную форму двоякой кривизны, а. линии постоянных прогибов образуют семейство гипербол, описываемых уравнением:

- Ц^Т = const. дх²    ду²

Уравнение асимптот к этим гиперболам имеет вид д 2ш д 2 ш дх2 Ц ду2

где ц - коэффициент Пуассона.

Так как полосы на интерферограмме отражают место равных уровней перемещений, а К_х = д^т является кривизной прогибов по оси х и дут по оси У, то уравнение (5) можно представить

Кх + цКу = const.(7)

Из выражения (8) можно определить коэффициент Пуассона:

К + цКу = 0.(8)

Кх ц = — К"у.

Таким образом, соотношение углов между асимптотами характеризует эффект Пуассона, определяемый через соотношение кривизн (9), которые определяют углы между асимптотами по интерферограмме (рис. 5).

Изгибная компонента деформаций поверхности образца представлена на рис. 5.

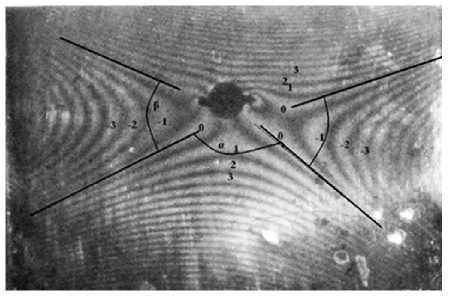
Рис. 5. Интерферограмма, растягиваемого образца, отражающая изгиб, измерение углов между асимптотами

По половине угла между асимптотами коэффициент Пуассона определяется:

^Е у

Е х

* = 0.32. tga

(Ю)

Для алюминиевых сплавов ц = 0.33, таким образом, измеренное значение отличается на 3%. Влияние нестандартного тонкого образца, с концентратором напряжений и системы нагружения его вызывает подобную картину полос, по которой мы определяли коэффициент Пуассона, однако в первом приближении мы можем воспользоваться данной методикой.

Обычно принято считать коэффициент Пуассона.

ЕУ

(И)

,

Ех где Ех, Еу - относительные деформации по осям X, У соответственно. Модули упругости Е л G обычно определяются в линейной постановке через деформации е ii напряжения ст по формулам упругости сопротивления материалов:

- = Ее; Е = ^- ;А- = ^ ;Ае = ^U ; Е =    ; G = ^Е

е       F        a      FU \     2(1 + ц)

где АР - дифференциальная нагрузка,

.    U_A    M_aU_x

Ае = — =----, a      ap

Ае - соответствующая дифференциальная относительная деформация, U \ - цена полосы на интерферограмме, a - шаг полос. М_ув = аф/а, аф - размер на фото-интерферограмме, Мув - масштаб увеличения.

По нашим измерениям: результаты для тонкого образца - модуль упругости Е = 76000 МПа. G = 28700 МПа. в справочных данных Е = (7 — 7.2)000 Мпа. По нашим измерениям: результаты для толстого образца - деформация е = 0.32 • 10^-3, модуль упругости Е = 7.8125 • 104 МПа.

Следует заметить, что экспериментальные данные могут отличаться от табличных справочных данных, основанных на стандартных измерениях типовых материалов. Использование экспериментальных измерений всегда предпочтительнее, так как они отражают особенности работы материалов в каждом эксперименте.

• 6.    Пример определения физико-механических характеристик толстого образца

• 7.    Выводы

Приведем пример определения физико-механических характеристик толстого образца из материала Д-16Т с геометрическими размерами: толщина б мм, ширина 36 мм, диаметр отверстия б мм. Ниже на рис. б приведены полученные спекл-интерферограммы, отфильто-рованные со спекл-голограммы на этапе нагружения дифференциальной нагрузкой 1,7 тс, образца из материала Д-16Т толщиной бмм, шириной 36 мм с отверстием диаметром 6 мм.

Рис. 6. Интерферограммы отфильтрованных компонент пространственных перемещений

В результате обработки и расшифровки данной спекл-голограммы двойной экспозиции получили: модуль упругости Е = 66 460 МПа, коэффициент Пуассона ц = — ел = 0.3, еж модуль сдвига, G = 25 560 МПа.

Предложенная методика, измерения модулей упругости и коэффициента. Пуассона, обладает простотой и приемлемой для практики информативностью. Она. позволяет определять физико-механические характеристики материалов при сложном нагружении и испытании натурных материалов и конструкций. Полученная на интерферограммах разница результатов для тонких и толстых образов является новшеством в экспериментальной механике испытания материалов.