Определение геометрических параметров ранее необработанных зон

В существующих САМ системах (включая высшего уровня UNIGRAPHICS, CATIA, PRO/ENGINEER) ядро построения объектов основано на твердотельном моделировании (parasolid- формат X_T) и, чтобы осущест-вить управление режимами резания, необходимо производить пошаговое вычитание модели обрабатываемой детали от модели заготовки. Но модель заготовки САМ системами строится фасетами (формат STL), и по этой при-чине современные САМ системы не в состоянии производить булевские опе-рации. Даже если допустить, что форматы детали и заготовки (от предыду-щей операции) будут совпадать, системе придется выполнять пошаговое определение срезаемого объема, что значительно увеличит время расчета управляющей программы.

При разработке управляющей программы САМ системы рассчитывают только траекторию движения инструмента. Технологом-программистом за-даются следующие параметры:

• □    рабочая подача;

• □    подача первого реза;

• □    подачи врезания и отвода инструмента;

• □    ускоренные подачи;

• □    частота вращения шпинделя.

Следует заметить, что значения этих параметров, не меняется в процессе отработки управляющей программы.

В этой связи возникает необходимость разработки нового способа, по-зволяющего воздействовать на процесс формообразования покадровым управлением режимами резания на любом участке обрабатываемой поверх-ности.

Для этого необходимо, чтобы система ЧПУ решала следующие задачи:

• □    определяла изменение геометрических параметров зоны обработки;

иводя их значение к оптималь-ным, на произвольном участке обрабатываемой поверхности.

Решение данных задач позволит обеспечить стабилизацию силовых пара-метров, влияющих на точность и качество обрабатываемых вогнутых фасон-ных поверхностей при чистовом объемном фрезеровании.

При объемном фрезеровании вогнутых фасонных поверхностей сферическими фрезами, движение инструмента обычно назначается по нормали к обрабатываемой поверхности. Данный способ позволяет уменьшить число рабочих и холостых движений, а также повышает точность и качество механической обработки. Траектория движения инструмента при объемной обработке представляет собой сплайн.

Для того, чтобы определить величину максимально возможного при-пуска, который формируется около впадины обрабатываемой поверхности, необходимо знать, по какой траектории движется инструмент. Однако со-временные системы САМ такой анализ автоматически не производят, для этого необходимо дополнительно строить сечения поверхности, что требует дополнительных затрат. Из работы Исходя из этого, будем считать, что параметр максимально возможного припуска одинаков для любого типа конического сечения, а так как математические преобразования с параболой проще воспринимаются системами ЧПУ и пара-метр максимального припуска формируется именно для сечений типа пара-болы, то расчет максимально возможного припуска произведем для парабо-лического участка.

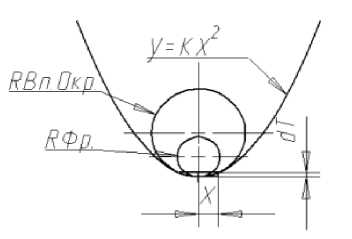
Рис.1. Схема расчета параметров параболы

Уравнение параболы:

y=kx2.

На участке параболы, который зависит от точности обработки ΔT мож-но построить окружность радиусом RВп*Окр. Из производственного опыта из-вестно, что максимальный радиус инструмента для обеспечения процесса ре-зания без дробления, должен быть меньше радиуса вписанной окружности в 1,1 раза. Следовательно, по построению Рис.1, коэффициент параболы k –зависит от радиуса сферы применяемого инструмента.

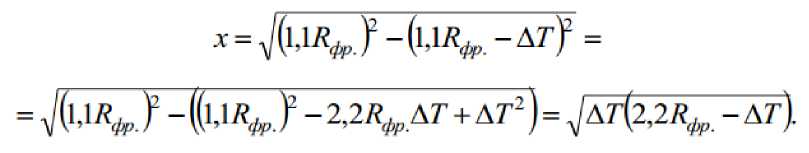
Из уравнения параболы:

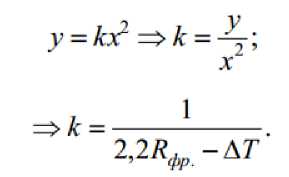
Окончательный получистовой переход выполняется цилиндрической фрезой, диаметр которой равен диаметру сферической чистовой фрезы. Следовательно, максимальное значение нарастающего припуска при обработке симметричной параболы определяется по выражению:

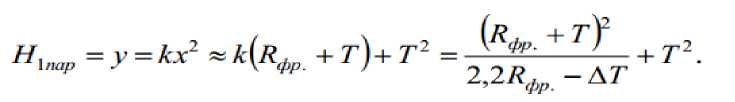
Выражение (2.5) рассчитывает параметр максимально возможного припуска, который может сформироваться при черновой обработке цилиндрической фрезой, при условии, что диаметр цилиндрической фрезы равен диаметру сферической.