Определение геометрических параметров совмещённых конических опор качения водила планетарно-цевочной передачи типа 2K-V

Введение. Планетарно-цевочные передачи, известные в отечественной технической литературе под условным обозначением 2K-V [1], благодаря компактности и возможности обеспечивать значительные передаточные отношения при сохранении высокой нагрузочной способности, кинематической точности, низкой виброактивности и высокому КПД, уже достаточно длительное время успешно применяются в качестве основных элементов силового привода звеньев промышленных роботов [2]. Данные механизмы, выполненные с тремя эксцентриковыми валами, традиционным эвольвентным зацеплением на первой быстроходной ступени и внецентроидным внутренним це- вочным зацеплением на второй тихоходной ступени, относятся к дифференциальным и могут применяться в машинах по различным вариантам сочетаний входных и выходных звеньев. При

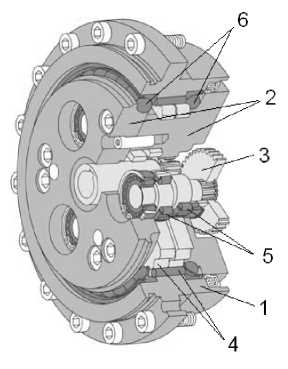
Рис. 1. Вариант трехваловой схемы планетарно-цевочного редуктора 2K-V фирмы «Nabtesco»: 1 – корпус; 2 – водило; 3 – эвольвентный сателлит быстроходной ступени; 4 – эпи-циклоидный сателлит и цевка вне-центроидного внутреннего цевочного зацепления; 5 – цилиндрические роликовые подшипники; 6 – шарики радиально-упорных совмещённых опор качения

этом передаточное отношение получаемых редукторов будет изменяться на единицу. Как правило, выходным звеном подобного типа планетарно-цевочных редукторов, является водило, закрепленное в подшипниках качения в корпусе редуктора. Необходимо отметить, что все силы, возникающие при передаче и преобразовании вращательного движения в зацеплении эвольвентной планетарной ступени и во внецентроидном внутреннем цевочном зацеплении второй ступени, за счет принятой трехваловой схемы передачи движения полностью уравновешиваются внутри корпуса и практически не оказывают силового воздействия на указанные подшипники качения. Однако силы инерции приводимых в движение водилом рабочих звеньев промышленных роботов, возникающие при их перемещении со значительными ускорениями, их вес и приложенные к ним рабочие нагрузки создают на водиле значительные опрокидывающие моменты и осевые усилия, непосредственно воздействующие на эти подшипники качения.

Геометрические параметры опор качения водила. На рис. 1 показан пример исполнения такого планетарно-цевочного редуктора, разработанный компанией «Nabtesco» (Германия), являющейся одной из ведущих в этом направлении зарубежных фирм.

Как видно из рисунка, рассматриваемые опоры качения выполнены в форме оригинальных радиально-упорных подшипников, внутренние кольца которых совмещены с корпусом водила, что представляет собой достаточно сложную в технологическом отношении конструкцию. Наружное кольцо выполнено отдельно и вставляется в корпус редуктора. В качестве тел качения в данных опорах качения используются шарики с точечным контактом (поз. 6). Применение подобной формы тел качения снижает динамическую и статическую грузоподъемность этих опор и ещё более усложняет технологию изготовления беговых дорожек, расположенных на корпусе водила. Увеличение динамической грузоподъемности в данном случае достигается за счет изъятия сепаратора и увеличения количества тел качения при более плотном их расположении в каждой опоре качения. Достаточно сложной представляется нам и регулировка рабочих зазоров, которая необходима для подобного типа узлов.

Переход в радиально-упорных подшипниковых узлах от точечного контакта тел качения к линейному дает возможность значительно увеличить их динамическую и статическую грузоподъемности. Это может быть достигнуто заменой в опорных узлах тел качения сферической формы на ролики, имеющие коническую форму [3]. Следует отметить, что применение в рассматриваемых опорных узлах стандартных радиально-упорных конических подшипников c необходимой грузоподъемностью, учитывая их значительные установочные размеры, может привести к увеличению общих габаритов редуктора и его массы, и в связи с этим является также нецелесообразным. Это особенно является актуальным при проектировании малогабаритных планетарно-цевочных редукторов с заранее заданными общими габаритными параметрами, определяемыми условиями их эксплуатации.

Проектированию и расчету опорных узлов водила должен предшествовать расчет всех элементов эвольвентной и цевочной передач и опорных узлов эксцентриковых валов. Выполняется также предварительная конструктивная проработка водила, всех входящих в него элементов и корпуса редуктора. Это все, в общем, дает возможность предварительно определить габаритные размеры опорных узлов водила и нагрузки, действующие на них с учетом внешних сил и моментов.

С учетом полученных значений радиальных и осевых нагрузок, действующих на совмещённые опоры качения водила, осуществляется подбор диаметральных и линейных параметров конических роликов с ориентацией на конические ролики, применяемые в стандартных радиально-упорных подшипниках. В зависимости от соотношения радиальных и осевых нагрузок ориентировочно выбирается угол контакта конического ролика в пределах 9–18° и угол конусности ролика, но так, чтобы вершина конуса ролика лежала на оси вращения водила. На рис. 2 показан один из вариантов компоновки таких подшипниковых опор (поз. 3) водила планетарно-цевочного редуктора типа ПЦР 3-36(6), разработанного авторами данной статьи.

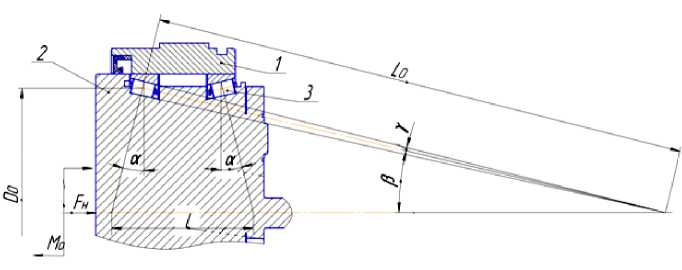
Рис. 2. Вариант компоновки совмещённых опор качения планетарно-цевочного редуктора типа ПЦР 3-36(6): 1 – корпус; 2 – водило; 3 – радиально-упорная совмещённая опора качения; α – угол контакта конического ролика; Мо – опрокидывающий момент; F H – внешняя осевая сила; L – расстояние между точками приложения опорных реакций; Lo – длина среднего конусного расстояния ролика; Do – диаметр центров комплекта роликов; β – номинальный угол контакта ролика; γ – угол конусности ролика

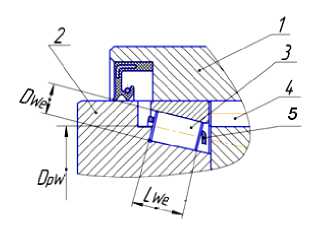
Рис. 3. Подшипниковый узел опоры водила: 1 – корпус редуктора; 2 – водило; 3 – конический ролик; 4 – цевка; 5 – сепаратор; D We – диаметр ролика; D pW – диаметр окружности центров торцов роликов; L We – длина ролика

Как видно из рисунка, совмещённые опоры качения ограничены, с одной стороны, параметрами водила 2 со всеми входящими в него элементами передач (на рисунке не показаны) и, с другой стороны, заданными габаритами корпуса редуктора 1. Внутренние кольца опор качения с беговыми дорожками выполнены заодно с корпусом водила. Наружные кольца являются вставными, что дает возможность за счет шлифовки их больших торцов регулировать рабочий зазор в подшипниках.

С целью получения необходимой динамической грузоподъемности подшипниковых опор при выборе диаметров конических роликов D We (рис. 3) необходимо ориентироваться на максимально возможные их размеры.

В соответствии с рекомендациями [4] диаметры роликов DWe можно принять из соотноше- ния

DWe = (0,5…0,53) h, где h = D – D0; D – диаметр наружной поверхности наружного кольца подшипника; D0 – диаметр окружности центров комплекта роликов (см. рис. 2).

При этом длина ролика определяется также в зависимости от величины h:

L We = (1,2…1,25)h.

Полученные значения D We и L We следует округлить до ближайших больших значений стандартных подшипников соответствующих серий. При этом следует расчётным путём проверить обеспечение достаточной прочности беговых дорожек, выполняемых на корпусе водила, и технологической жесткости наружных колец подшипников, устанавливаемых в корпусе передачи.

Угол при вершине конуса ролика α р = 2γ, как видно из рис. 2, жестко связан с углом контакта ролика α и расположением роликов относительно оси вращения водила, определяемым диаметром их центров D 0 . Значение диаметра D 0 непосредственно зависит от габаритов водила и размеров входящих в его состав деталей, которые, как правило, при предварительной конструктивной проработке принимаются минимальными. В связи с этим углы контакта ролика обычно задаются.

Применение конических роликов по размерам соответствующих роликам стандартных подшипников не всегда оказывается возможным. Это связано прежде всего с тем, что для стандартных радиально-упорных подшипников диаметр центров конических роликов обычно не совпадает с диаметром центров роликов проектируемой совмещённой опоры качения. Обеспечение совпадения вершины конуса ролика с осью вращения водила приходится осуществлять за счет изменения угла контакта. Во многих случаях это приводит к значительному увеличению угла контакта ролика, и совмещённая опора качения приобретает свойства упорно-радиального подшипника, а в некоторых случаях это оказывается вообще невозможным.

Увеличение угла контакта ролика приводит к нежелательному снижению динамической радиальной грузоподъемности подшипниковой опоры водила. Это является очевидным при рассмотрении зависимости для ее определения, имеющей вид [5]

С=bmfc(iLWecos α)7/9Z3/4 DWe29/27, где С – динамическая радиальная грузоподъемность подшипника; bm – коэффициент, характеризующий свойства стали с учетом способа ее изготовления; fc – коэффициент, зависящий от геометрии деталей подшипника, точности их изготовления и материала; i – число рядов роликов в подшипнике; LWe – длина ролика, мм; α – угол контакта ролика; Z – число роликов в однорядном подшипнике; DWe – диаметр ролика, мм.

Увеличение угла контакта ролика α уменьшает значение cos α и соответственно снижает значение динамической радиальной грузоподъемности подшипника. Кроме этого величина коэффициента f c определяется по табличным данным в зависимости от отношения (D We cos α )/D 0 , и при его уменьшении уменьшается и величина этого коэффициента, оказывая также отрицательное влияние на динамическую грузоподъемность подшипника.

Необходимо также учитывать, что в радиально-упорных подшипниках действует и гироскопический момент, связанный с изменением направления оси вращения роликов в пространстве, T г .

Т г = Iω р ω с sin α , где I – момент инерции ролика относительно своей оси вращения; ω р – угловая скорость ролика вокруг своей оси; ω с – угловая скорость вращения сепаратора; α – угол контакта ролика.

Увеличение гироскопического момента при увеличении угла контакта ролика отрицательно влияет на работоспособность подшипников, увеличивает износ как тел качения, так и беговых дорожек.

В связи с изложенным при принятых по ранее приведенным рекомендациям значениях диаметра ролика D We и его длины L We , по всей видимости, следует задаваться углом контакта ролика α в пределах 9–19° в зависимости от характера и соотношения сил, действующих на подшипниковые опоры водила, а угол конусности ролика α р = 2γ уточнять расчетным путем. При этом возможна последующая коррекция угла конусности ролика за счет незначительного изменения угла контакта ролика.

В случае незначительных отклонений по конусности стандартного конического ролика не исключается возможность его применения в подшипниковом узле водила с корректировкой угла контакта. По завершению определения всех геометрических параметров совмещённых опор качения водила уточняются точки приложения опорных реакций и расстояние между ними, окончательно определяются нагрузки, действующие на них. По приведенной выше зависимости определяется динамическая грузоподъемность проектируемых опор качения и по принятой стандартной методике рассчитывается для наиболее нагруженной из них эквивалентная рабочая нагрузка. Заключение. Полученные результаты служат для определения ресурса работы совмещённых опор качения водила, который, в конечном итоге, сравнивается с заданным. При необходимости уточняются геометрические параметры и повторяется силовой расчет рассматриваемых опор качения.