Определение границ изменения внешних параметров, усложняющих расчет подвески сельскохозяйственной техники

Современное развитие технических машин в различных сферах человеческой деятельности требует постоянного повышения требований к их характеристикам. Это приводит к появлению новых научно-технических проблем, решение которых обеспечивает рост производственных возможностей общества1. Одним из примеров повышения эффективности использования автотракторной техники в сельскохозяйственной отрасли служит вопрос повышения надежности ее элементов подвески2 [1; 2].

Проблематика надежности во многом характеризуется ее взаимосвязью со всеми этапами жизненного цикла рассчитываемого узла, начиная от проектирования и изготовления и заканчивая использованием и последующим списанием вышедшего из строя изделия3 [3]. Все этапы жизненного цикла вносят свой вклад в решение комплексной задачи создания машины требуемого уровня надежности при минимизации затрат времени и финансов. Решения, принятые на этапе проектирования, в значительной мере определяют эксплуатационные и экономические показатели рассчитываемого изделия. Указанные параметры не являются независимыми. Определение существующей взаимосвязи между ними во многом помогает решать оптимизационную задачу получения максимальных эксплуатационных показателей при заданных исходных параметрах рассчитываемого узла [4–7].

В этой связи в статье представлен пример алгоритма одного из показателей, определяющих надежность и качество проектируемого изделия – координат опасного сечения рабочего узла. Рассматривается проблема расчета прочности вала привода колес сельскохозяйственной техники на основании допущений механики сплошных сред. Учитываются условия прочности как наибольшего крутящего момента, так и величины относительных деформаций вала4 [1; 8]. Задачей исследования является разработка способа определения области фазового пространства изменения внешних воздействий на элемент конструкции, обусловленных распределенным весом автотракторной техники, при которых необходимо построение не только эпюр моментов и деформаций, но и определение экстремальных значений на каждом участке, где изменение показателя прочности конструкции нелинейно.

В наиболее общем виде расчеты нагруженного вала на прочность необходимо вести по нескольким показателям: предельная нагрузка от действия изгибающего момента, предельная нагрузка от поперечной силы и величина допустимой деформации оси вала5 [9–11]. Общее заключение о несущей способности детали можно делать на основе анализа всех вышеперечисленных факторов.

В настоящий момент в подавляющем большинстве случаев комплексные расчеты деталей машин на надежность и долговечность не производятся. Кроме того, нет единой схемы производства таких расчетов6 [6; 12; 13]. Инженеры ограничиваются отдельными показателями, не способными характеризовать работу изучаемого узла в целом в течение всего жизненного цикла.

Обзор литературы

Исследование поведения поперечно нагруженных симметричных балок, является начальным этапом изучения работы упругих твердых тел в рамках сопротивления материалов в технических вузах. Предваряют это изучение лишь симметричные растяжения и сжатия тел правильной формы7 [14; 15].

Первые систематические исследования работы балок на изгиб были проведены французским ученым Ма-риоттом8 [11]. Помимо прочности материалов, его также интересовала упругая составляющая процесса деформирования. В своих экспериментах с поперечно нагруженными симметричными балками (схема эксперимента представлена на рисунке 1) он показывает, что разрушение наступает тогда, когда удлинение конструкции превышает некоторое предельное значение (варьируемый параметр – d)9 [16].

A BC D E y A S ^d J ^x

Р и с. 1. Опыты Мариотта на изгиб

F i g. 1. Marriott's bending experiments

Далее Мариотт замечает, что волокна в нижней части поперечного сечения испытывают сжимающие усилия, в то время как волокна верхней части – растянуты. Прочность растянутых волокон в этом случае будет равна половине значения прочности всей конструкции, аналогичные рассуждения он проводит и для сжатых волокон. Однако получить правильное соотношение для прочности всей конструкции ему помешал некорректный расчет площади поперечного сечения.

Для определения уравнения изогнутой оси балки Я. Бернулли впервые использует аппарат математического анализа. Он вводит понятие кривизны кривой изгиба и определяет ее взаимосвязь с величиной изгибающего момента10 [17; 18]. Более детально этот вопрос разработал в дальнейшем Эйлер, решая задачу о цепной линии с использованием аппарата вариационного исчисления [14; 19].

Предел прочности балки в своих трудах впервые описал Кулон, анализируя уравнения статики для горизонтальных и вертикальных составляющих внутренних усилий в рассматриваемом сечении. Он аналитически установил, что центром поворота изгибающийся балки является не нижняя ее кромка, а ось симметрии11.

В 1826 г. Навье впервые описывает не определение предельных нагрузок конструкций, как делали до него, а расчет предельного значения внешних воздействий на тело, при котором оно ведет себя еще упруго12 [8]. Полагая прогибы, возникающие в балке, малыми, он определяет зависимость:

EJz • d-y = M, (1) dx где Jz – момент инерции сечения балки; M – величина изгибающего момента в рассматриваемом сечении относительно нейтральной оси, а система координат вводится так, как представлено на рисунке 1. Ею он пользуется для любого случая поперечного нагружения простой балки.

Сен-Венан, используя аппарат математической теории упругости, показал, что при расчетах балок методами сопротивления материалов можно пользоваться рядом существенных допущений [11]:

– поперечные сечения балок остаются плоскими при деформировании;

– продольные волокна балки не оказывают какого-либо воздействия друг на друга, испытывая лишь растяжение/ сжатие.

Однако, несмотря на значимость вышеперечисленных исследований, не все результаты, полученные в них, нашли отражение в существующих методах расчета элементов конструкций на прочность используемых инженернотехническим составом.

В настоящий момент расчеты на прочность проводятся с использованием ГОСТ 27609-88 «Расчеты и испытания на прочность в машиностроении» по направлениям применения рассматриваемых деталей и механизмов. Если точности моделей, предусмотренных допущениями сопротивления материалов, достаточно для расчетов элементов конструкций, то нормативных документов, определяющих алгоритм такого расчета, оказывается достаточно. Здесь возможны исключения, когда определение критических значений внутренних усилий таким способом существенно неверно. Залогом правильного определения прочностных показателей рассчитываемой детали является корректное определение опасного сечения в рассматриваемом случае. Этой цели посвящена настоящая статья.

Материалы и методы

В современной инженерной практике есть определенные трудности в использовании конечных соотношений по расчету различных элементов конструкций с использованием аппарата механики сплошных сред13 [4]. В этой связи целесообразным видится разработка рекомендаций при производстве инженерных расчетов, позволяющая, в случае необходимости, проводить корректировку определения опасных сечений либо величин внутренних усилий, возникающих от действия внешних факторов на рассматриваемую деталь.

Схема расположения вала привода колеса в системе подвески автотракторной техники представлена на рисунке 2. Сила P характеризует контакт полуоси со ступицей колеса, распределенная нагрузка q – нагрузку от частей дифференциала. Представленная модель во многих случаях адекватно описывает напряженно-деформированное состояние работы вала.

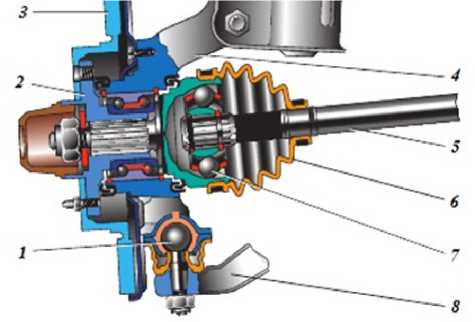
Р и с. 2. Механизм крепления вала привода колеса:

1 – шаровая опора; 2 – ступица; 3 – тормозной диск; 4 – поворотный кулак;

5 – вал привода переднего колеса; 6 – защитный чехол; 7 – наружный шарнир вала;

8 – нижний рычаг

F i g. 2. Wheel drive shaft mounting mechanism:

1 – spherical bearing; 2 – hub; 3 – brake disk; 4 – rounded fist; 5 – front wheel drive shaft; 6 – protective case; 7 – external shaft joint; 8 – lower arm

В качестве модели работы вала принимается статически определимая симметричная поперечно нагруженная стальная балка, представленная на рисунке 3.

При определении напряжений и деформаций в рассматриваемой детали приняты допущения механики сплошных сред. Вводится пространственная декар-товая прямоугольная система координат. Начало координат находится в точке А (рис. 3), о сь Аx совпадает с направлением вектора AB , ось Аy направлена вдоль линий действия сил (направлен и е совпадает с направлением вектора P ), ось Аz – перпендикулярно плоскости рисунка, причем направление выбрано так, что указанные оси образуют правую тройку векторов.

R a      P

AD

/27ШЛШ л a1

y

В качестве материала изготовления детали используется конструкционная сталь, для которой определены основные показатели, характеризующие ее механические свойства: плотность, модуль Юнга, коэффициент Пуассона.

Сечение вала плоскостью Axz – круг, радиуса d . Для него момент инерции

Л т    ^Kd⁴

относительно оси Az : J z = ^ .

Длина вала принимается: а . Расстояния AD и CB (рис. 3) полагаем: а₁ и а₂ . Усилие, передаваемое от веса заданной единицы техники на левую оконечность вала, примем P (площадь контакта много меньше длины вала), распределенная нагрузка в месте крепления вала

R b

q

C 0              B

x a2

Р и с. 3. Модель работы вала привода колеса

F i g. 3. Model of the wheel drives haft

с дифференциалом: q (значительная площадь контакта обуславливается жесткими режимами эксплуатации сельскохозяйственной техники).

Расчеты на прочность проводятся исходя из условия максимального изгибающего момента, возникающего в поперечном сечении детали14 [20; 21].

Результаты исследования

Методами статики определяем значения сил реакции, возникающих в вале на примере сеялки Väderstad RAPIDRD 300 при P = 1,5 кН, q = 12,5 кН/м, а = 0,7 м, а 1 = 0,1 м, а 2 = 0,2 м, d = 0,04 м, R_a = 1,64 кН, R_b = 2,36 кН. На основе полученных данных строим эпюру изгибающего момента для всей балки (рис. 4).

Максимальное значение изгибающего момента при данном виде нагружения реализуется в сечении, проходящем через точку N (рис. 4) нормально к оси симметрии вала (расчеты проводились с использованием пакета математических программ Maple). Расстояние AN = 0,51 м.

Для определения прогибов вала вдоль всей длины воспользуемся соотношением (1). Для уравнений ординат прогибов будем иметь:

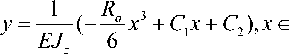
[ 0, a l )

1 P - R ₃ Pa ₂ y =---- (----- — x ³--¹ x ² +

EJ 62

+ C 3 x + C 4 ), x e [ a 1 ,a - a 2 )

1 , q ₄ P - R_a - q ( a - a ₂) ₃ y =-- (— x ⁴ +---- a——---— x ³ +

EJ 24           6

₊ q(a ^- a 2 ) 2 ^- 2 Pa i x 2 ₊

+ C 5 x + C 6 ), x e [ a - a 2 ,a ]

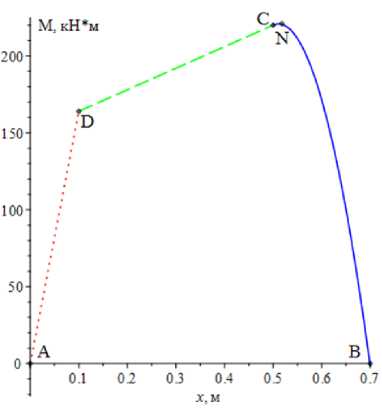
Р и с. 4. Эпюра изгибающего момента поперечно нагруженного вала

F i g. 4. Diagram of the bending moment which perceives a transversely loaded shaft

Неизвестные постоянные интегрирования определяются из начальных и граничных условий: прогибы в точках А и В равны нулю, прогибы слева и справа соответственно от точек С и D совпадают (нет разрывов вала), касательные в указанных точках также совпадают с обеих сторон (нет изломов вала). В итоге получаем следующую систему линейных уравнений:

' C 1 _ C 3 _ 10 C 4 ₌ _ 5

C i _ C з =_ 6,1

C 3 + 2 C 4 _ C 5 _ 2 C 6 = 195,3

C 3 _ C ₅ = 260,42

C 6 =_ 0,7 C ₅ _ 110

_ C2 = 0

Определитель указанной системы отличен от нуля, следовательно, существует единственное решение, представимое следующей точкой в шестимерном пространстве констант: {55,6; 0; 63,1; ‒0,25; ‒197,32; 32,3} .

Таким образом, для уравнения изогнутой оси вала15 окончательно будем иметь:

y = - 0,1 x ³ + 0,02 x , x e [ 0, a 1 ) y = - 8,84 - 10 ^{- 3} x ³ - 0,03 x ² +

< + 0,02 x - 9,48 • 10 ^{- 5}, x e [ a 1 ,a - a 2 ) . (4) y = 0,2 x ⁴ - 0,4 x ³ + 0,27 x ² -

- 0,07 x + 0,01, x e [ a - a 2 , a ]

Такое положение дел приводит нас к необходимости более детального исследования уравнения изменения момента на исследуемом участке. Указанный случай обычно не учитывается в инженерных расчетах валов на прочность. Реализация такого сценария происходит, когда абсцисса вершины параболы CNB (рис. 4) расположена правее точки С . В общем случае она определяется следующим соотношением:

x max

— a +

⁽ a - a 2^{) 2}

2 a

—

a 1

a

P

, ^q

Графически выражение (4) представлено на рисунке 5. Максимальный прогиб реализуется на участке DC.

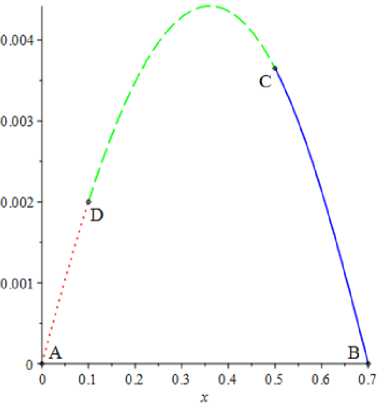
Р и с. 5. Уравнение изогнутой оси вала

F i g. 5. Curved shaft axis equation

и является функцией пяти параметров. Условно их можно разделить на две группы. К первой относятся параметры, определяющие координаты точек приложения внешних нагрузок на вал: a, а ₁ , a ₂; ко второй – интенсивность приложенных усилий: P , q .

Принимая характер распределения внешних воздействий на вал неизменным (считаем, что расчет производится по заданному проекту компоновки подвески автотракторной техники – на примере сеялки VäderstadRAPIDRD 300), координаты опасного сечения будут определяться интенсивностью внешних воздействий на вал:

Зададимся теперь целью определения всех таких вариантов нагружения вала, при которых опасное сечение расположено не на границе двух зон с заданным законом распределения момента, проходящим через точку С , а на участке СD .

15 Timoshenko S. P. Strength of materials. P. 1.

p xmax = 0,53 - 0,14 - . (6) q

Для определения зоны изменения параметров Р-q исходим из следующих предположений. Диапазон изменения величины x _max задан интервалом ( а-а ₂, а ]. Значения внешних воздействий положительны. Накладывая указанные условия на зависимость (5) получим графическое представление искомой области (рис. 6).

Численное решение указанной системы неравенств методом перебора с использованием пакета математических программ Maple позволило определить

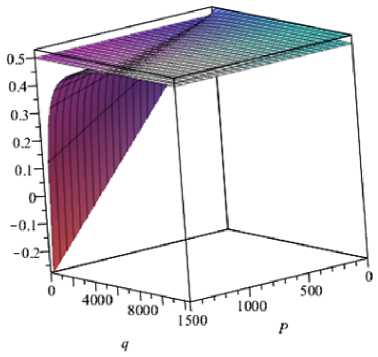
а)

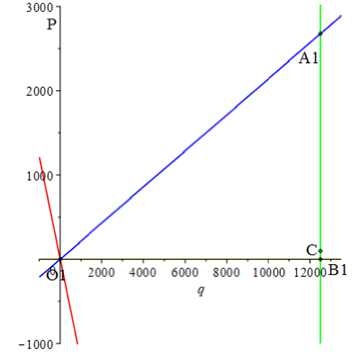
b)

Р и с. 6. Критическая область изменения внешних воздействий, приводящая к необходимости проведения дополнительных расчетов: а – абсцисса опасного сечения как функция внешних воздействий;

b – область кривой (6), находящаяся выше плоскости x = 0,5 м

F i g. 6. Critical area of change the external influences, leading to the need for additional calculation: a – abscissa of the dangerous section as a function of external influences;

b – area of the curve (b) above the plane x = 0.5 m значение параметров Р-q, при котором отклонение точки экстремума на эпюре изгибающих моментов от точки С (рис. 4) будет иметь место. Это позволит определить наиболее невыгодное положение существующей системы расчета вала на прочность, дав максимальное различие с результатами, полученными с использованием предложенной методики. Найденная область изменения параметров внешнего воздействия О1А1В1 изображена на рисунке 6 b. Красная прямая определяет здесь полуплоскость, задаваемую неравенством xmax > 0,5, синяя – полуплоскость xmax < 0,7. Точкой C обозначено напряженное состояние, рассматриваемое на рисунках 3–5. Она принадлежит треугольнику О1А1В1, что и позволяет говорить в рассматриваемом случае о необходимости проведения скорректированного расчета.

Обсуждение и заключение

В результате авторами получена область О1А1В1, представленная на рисунке 6, которая определяет границы

изменения усилий, воспринимаемых валом от внешних воздействий, при которых координаты расположения опасного сечения не являются очевидными и не всегда корректно определяются при производстве инженерных расчетов деталей подвески сельскохозяйственной техники на прочность согласно ГОСТ 27609-88. В этом случае исследования необходимо продолжить, определив координаты поперечного сечения, в котором реализуется экстремум величины изгибающего момента на интервале ( а-а ₂, а ] изменения координаты вдоль оси симметрии вала, а затем определить его значение. Разработанная в среде Maple программа позволяет для данного типа нагрузки определить область изменения внешних параметров, а в случае выхода значений нагрузки за указанные границы – провести скорректированный расчет опасного сечения в полуоси, дающего возможность более точно произвести расчет всей детали на прочность.

Q ИНЖЕНЕРНЫЕ ТЕХНОЛОГИИ И СИСТЕМЫ Том 33, № 2. 2023

Поступила 13.02.2023; одобрена после рецензирования 14.04.2023; принята к публикации 24.04.2023

Все авторы прочитали и одобрили окончательный вариант рукописи.

Available at: https://cyberleninka.ru/article/n/opredelenie-napryazheniy-v-galvanicheskom-kompozitnom- pokrytii-s-uchetom-teorii-dislokatsiy/viewer (accessed 11.02.2023). (In Russ., abstract in Eng.)

Submitted 13.02.2023; revised 14.04.2023; accepted 24.04.2023