Определение границ участков динамограммы при ее обработке

¹ Введение . Одной из ключевых задач при скважинной добыче нефти является диагностика состояния скважины и добывающего оборудования. Самым распространенным способом диагностики является анализ динамограмм, т.е. зависимостей нагрузки на полированном штоке от перемещения штока при его полном двойном ходе. Внутри динамограммы есть участки, характеризующие каждую фазу движения полированного штока. Возможные варианты динамограмм с разными дефектами оборудования приведены, например в [1].

Автоматизированная обработка динамограммы может производиться на основе двух различных подходов к решению этой задачи. При первом подходе на основе всей динамограммы целиком получаем какое-то значение критерия, по которому судим о дефектах скважины и оборудования. Такой подход применялся, например в [2]. При втором подходе вся динамограмма разбивается на отдельные участки, и дефекты определяются по поведению динамограммы на этих участках. Такой подход описан в [3]. Автору представляется более интересным второй подход, так как обработка всей динамограммы целиком может представлять большую вычислительную и алгоритмическую задачу.

При формализации этого подхода главной задачей будет являться процедура определения точек начала/конца характерных участков динамограммы. На границах участков из-за изломов (или переходов) меняется спектр сигнала. Это можно использовать для локализации участков динамограммы. Для этой цели можно применить вейвлетное преобразование сигналов, так как сама динамограмма представляет собой периодическую кривую.

Любую функцию s ( t ), принадлежащую гиль-бертовому пространству, можно разложить в ряд по базису V mk ( t ) [4,5]:

ю

• s ⁽ t ) = Е s mk V mk ⁽ t ),                      ⁽¹⁾

• m, k =-^

где s_mk – проекции сигнала на ортогональный базис функций. Они могут быть определены скалярным произведением по формуле²

^

s mk = ( s ⁽ t ), V mk ⁽ t )) = f s ⁽ t ) ■ V mk ⁽ t ) ' ^dt .       (2)

-Ю

Вейвлет-функция v ( t ) должна удовлетворять следующим требованиям [6]: ее интеграл +^

f v ( t ) ■ dt ⁼ 0; сама функция принадлежит про- -^

+^

странству Гильберта L 2 [R ] ( f V 2 ( t ) ■ dt конечен).

-^

Вейвлетный базис функционального пространства образуется путем масштабных преобразований и сдвигов порождающего вейвлета у ( t ):

у ( a , b , t ) = | a | ^1/2-y [( t-b )/ a ], a , b e R , a ^ 0,

V ( t ) e L ²( R ). (3)

Анализ согласно (3) начинаем со значения a = 1 в сторону увеличения его значения. Для нашего случая ищем проекцию только порождающего вейвлета для всех значений сдвигов b . Смотрим поведение этой функции. Вблизи точек перегиба эта функция резко меняет свое значение. Это и можно использовать в качестве индикатора смены участка динамограммы.

Варианты выбора порождающих вейвлетов и результаты моделирования

В качестве примера рассмотрим развернутую динамограмму, изображенную на рис. 1 (величины по осям условные). Ось перемещений дана в нормированном виде в диапазоне от 0 до 1 (0–0,5 – движение полированного штока вверх, 0,5–1 – вниз).

Рассмотрим варианты выбора порождающего вейвлета, так как от него зависят алгоритмы определения точек перегиба динамограммы. Автором было рассмотрено большое количество таких функций, некоторые из которых приведены в данной статье.

В качестве порождающего вейвлета примем функцию

ф( t ) = e *5 t • cos(62,8 • t ),                        (4)

где выбор коэффициентов функции обусловлен следующим: условное суммарное время всех участков принимаем равным единице; нас будут интересовать составляющие на порядок большие, чем частота движения полированного штока; затухание порождающей функции на границах ее периода задаем большим 3. График этой функции показан на рис. 2.

На рис. 3 приведены графики развернутой динамограммы и функции sb (масштабированные значения).

Видно, что график sb по форме практически повторяет график динамограммы и на нем заметны колебания, характерные для порождающей функции. Это говорит о слабой пригодности порождающего вейвлета класса (4) для определения гра- ниц участков.

Рассмотрим порождающий вейвлет:

' 0, t <  0;

• _V ( t ) = J 1,^{0 5} t ⁵ 0,02;

  - 1/3, 0,02 <  1 5 0,08;

0, t >  0,08.

График этой функции приведен на рис. 4, а на рис. 5 приведены масштабированные графики исходной динамограммы и функции s_b .

Из рис. 5 видно, что вейвлет (5) можно ис-

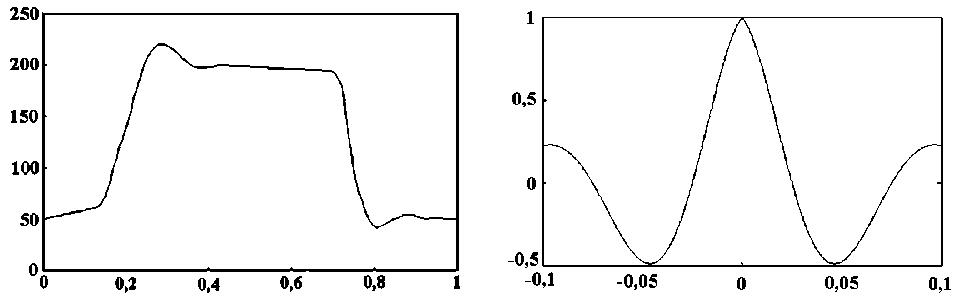
Рис. 2. График порождающей функции

Рис. 1. Динамограмма развернутая

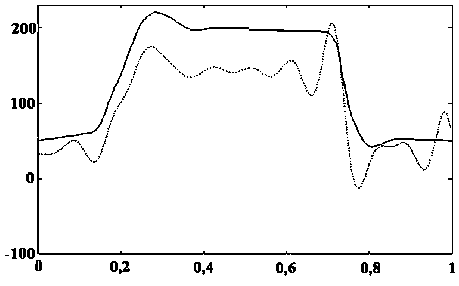
Рис. 3. Значения коэффициента разложения и исходная динамограмма

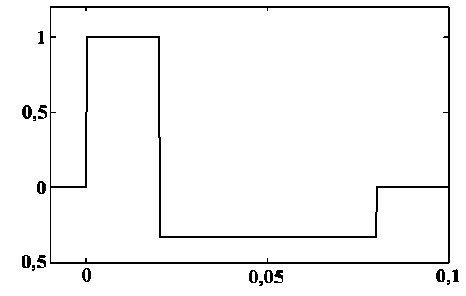
Рис. 4. График порождающей функции

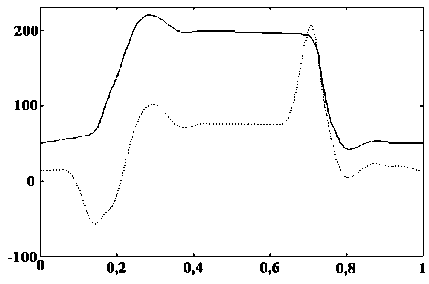
Рис. 5. Значения коэффициента разложения и исходная динамограмма

Рис. 6. График порождающей функции

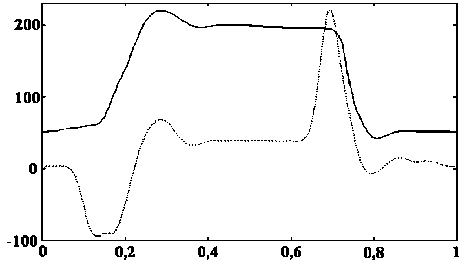
Рис. 7. Значения коэффициента разложения и исходная динамограмма

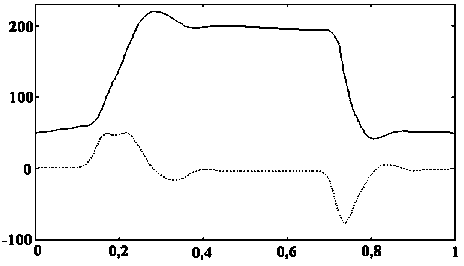
Рис. 8. Значения коэффициента а 1 разложения типа y = a q + a ^ ■ x и исходная динамограмма

пользовать для определения точек перегиба динамограммы. Подобными свойствами обладает и порождающий вейвлет:

' Q, t <  Q;

5Q ■ t , Q <  t <  Q,Q2;

V ( t ) =

• 1,    Q,Q2 <  t <  Q,Q4;

  - Q,75, Q,Q4 <  t <  Q,Q8;

Q, t >  Q,Q8.

График этой функции приведен на рис. 6, а на рис. 7 приведены масштабированные графики исходной динамограммы и функции s_b .

Для сравнения на рис. 8 приведены данные по расчету с использованием линейной модели. Коэффициенты модели получались с использованием метода наименьших квадратов. При этом для расчета коэффициентов брался интервал по оси x [ b - Q,Q25; b + Q,Q25] с шагом Q,QQ5. Далее вводился аналогично вейвлет-преобразованию сдвиг по всей оси от Q до 1.

Из всех этих зависимостей видно, что точки начала участков здесь можно определить как точки локальных максимумов/минимумов коэффициентов вейвлет-разложения или точки пересечения оси абсцисс с графиком a 1 ( b ) после прохождения локального максимума/минимума. Интересным вариантом является комбинация использования

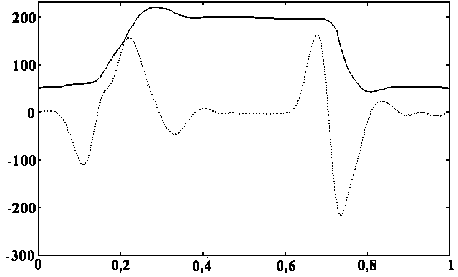
Рис. 9. Значения коэффициента a i разложения типа y = a _Q + a 1 ■ x по вейвлету (5) и исходная динамограмма

линейной модели и вейвлет-аппроксимации. На рис. 9 приведены графики исходной динамограммы и коэффициента a 1 модели y = a _Q + a 1 ■ x , полученной в результате обработки коэффициентов вейвлет-разложения типа (5).

Из графиков видно, что началом интервала здесь является точка пересечения оси абсцисс и зависимости a 1 ( b ) после локального максиму-ма/минимума.

Таким образом, задача свелась лишь к выбору зоны нечувствительности при фиксации локальных максимумов/минимумов.

Общий алгоритм получения границ участков динамограммы

Можно вывести общий алгоритм получения границ интервалов.

• 1.    Всю развернутую диаграмму заполняем по горизонтали точками b с каким-либо шагом (можно равномерной сеткой).

• 2.    Для каждой точки исходной динамограммы, используя порождающий вейвлет у ( t ) согласно (5), вычисляем значения коэффициента разложения в ряд s_b по формуле (2).

• 3.    Для каждой точки исходной динамограммы, используя модель вида y = a 0 + a 1 ■ x , вычисляем зависимость a 1 ( b ) по методу, например, наименьших квадратов.

• 4.    Для каждой точки коэффициента s_b , используя модель вида y = a 0 + a 1 ■ x , вычисляем зависимость a 1 _S ( b ) по методу, например, наименьших квадратов.

• 5.    Путем анализа поведения функций s_b , a 1 ( b ) и a 1 _S ( b ) определяем точки начала участков.

Примечание: так как вейвлет-функция достаточно быстро затухает, вместо интеграла на бесконечном отрезке из (2) можно использовать конечный отрезок.

Для анализа поведения функции s_b можно предложить следующую последовательность действий:

• 1.    Вычисляем точки максимума s max и минимума 5 min функции s b на диапазоне b е [0;1].

• 2.    Поскольку s max и s min имеют разные знаки, то в качестве зоны нечувствительности можно использовать зону [ 8 s _min; 8 s _max ], 8е (0;1). Смотрим точки пересечения кривой S b с прямыми 8 s max и 8 s min . Между ними должна находиться точка локального максимума/минимума. Она является претендентом на точку начала участка.

• 3.    По значению абсциссы и ординаты претендента и значению этих координат ближайших претендентов делается вывод о правильности определения точки начала участка. Для этого несложно сформировать какой-либо алгоритм фиксации точки начала каждого участка с учетом поведения и значений точек исходной динамограммы при этом значении абсциссы b .

• 4.    Если алгоритм фиксации точек дает неверный результат, то меняем зону нечувствительности (меняем значение 8 ) и продолжаем алгоритм с действия 2.

Для анализа поведения коэффициентов разложения функций a 1 ( b ) и a 1 _S ( b ) можно предложить следующую последовательность действий.

• 1.    Вычисляем точки максимума a max и минимума a _min функции a 1 ( b ) на диапазоне b е [0;1].

• 2.    Поскольку a max и a min имеют разные знаки, то в качестве зоны нечувствительности можно использовать зону [ 8 a min ; 8 a max ], 8 е (0;1). Смотрим точки пересечения кривой a 1 ( b ) с прямыми 8 a _max и 8 a min . Между ними должна находиться точка локального максимума/минимума. Точка пересечения с абсциссой после локального макси-мума/минимума – претендент на точку начала участка. Надо также следить, пересекают ли линии зависимости a 1 ( b ) слева и справа от точки локального максимума/минимума ось абсцисс.

• 3.    По значению абсциссы и ординаты претендента и значению этих координат ближайших претендентов делается вывод о правильности определения точки начала участка.

• 4.    Если алгоритм фиксации точек дает неверный результат, то меняем зону нечувствительности (меняем значение 8 ) и продолжаем алгоритм с действия 2.

Проверка одного алгоритма на модельных примерах

Рассмотрим работу алгоритма при использовании функции a 1 ( b ), полученной на основе обработки результатов линейной аппроксимации функции s_b , использующей порождающий вейвлет (5). Примерный вид такой обработки графически показан на рис.10.

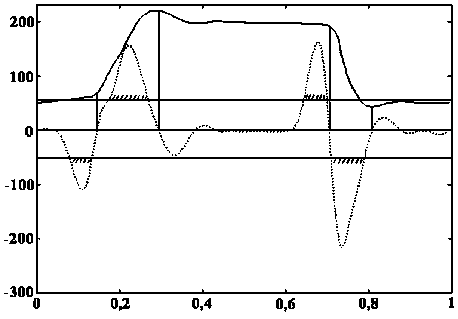
Рис. 10. Результаты обработки динамограммы (определение границ участков)

Здесь штриховкой показаны участки выхода графика a 1 ( b ) за границы зоны нечувствительности, а линиями – точки-претенденты на начало участка (потенциально существенные точки перегиба). Из графика видно, что эти точки получаются с некоторой (хотя и вполне допустимой) погрешностью. Это связано с конечностью импульса порождающей функции (рис. 10) и сглаживанию благодаря используемому методу наименьших квадратов (для вычисления коэффициента a 1 использовался участок [ b - 0,025; b + 0,025]).

Вообще говоря, точки развернутой динамограммы снимает какое-либо цифровое устройство (обычно микроконтроллер), поэтому можно использовать быстрые цифровые алгоритмы, но в данном случае это несущественно, так как динамограммы не обрабатываются на контроллере в реальном масштабе времени.

Рассмотрим развернутую динамограмму, изображенную на рис. 11 (величины по осям условные). Ось перемещений дана в нормированном виде в диапазоне от 0 до 1. Эта динамограмма не является стандартной и составлена для случая удара плунжера внизу и большого давления газа у приема насоса. Форма динамограммы была немного искажена, имитируя реальные условия съема динамограммы.

На рис. 12 приведены масштабированные графики исходной динамограммы и функции s_b , полученной с использованием вейвлета (5).

На рис. 13 приведены графики исходной динамограммы и коэффициента а 1 модели y = a ₀ + а 1 ■ x , полученной в результате обработки коэффициентов вейвлет-разложения типа (5).

Результаты обработки динамограммы по описанному ранее алгоритму приведены на рис. 14.

Из рис. 14 видно, что точка, соответствующая обратному выбегу кривой динамограммы (третья слева вертикальная линия), может быть получена как точка участка. Здесь надо учитывать:

• -    предполагаемый номер участка;

• -    значение усилия на штоке в начале и конце предполагаемого участка;

• -    общий диапазон изменения усилия на предполагаемом участке;

• -    общий диапазон усилий динамограммы.

Несложно сформировать набор таких правил, характерных для каждого участка.

Примечание: так как возможны выбросы точек динамограммы из-за сбоев аппаратуры и технических причин (легкое заедание механизмов и пр.), то для логического исследования полученных точек лучше всего использовать не исходную динамограмму, а ее усредненную кривую. Она отражает все особенности исходной динамограммы, но является немного сглаженным ее вариантом. На рис. 15 приведены графики исходной и усредненной динамограммы, каждая точка которой есть среднее арифметическое точек исходной динамограммы G ( s ) на интервале [ s - 0,025; s + 0,025]. При снятии динамограммы, например, микроконтроллером с АЦП, исходная динамограмма, в отличие от показанной на рис. 15, будет еще и зашумлена. Усреднение уменьшит величину шума.

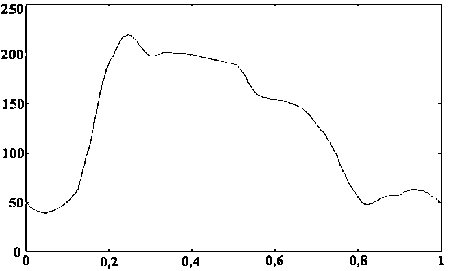
Рис. 11. Динамограмма развернутая

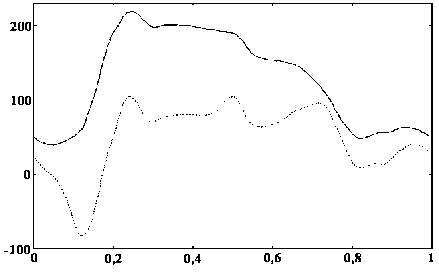
Рис. 12. Значения коэффициента разложения и исходная динамограмма

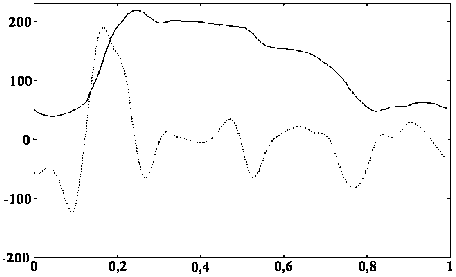
Рис. 13. Значения коэффициента а 1 разложения типа y = a 0 + а_г ■ x по вейвлету (5) и исходная динамограмма

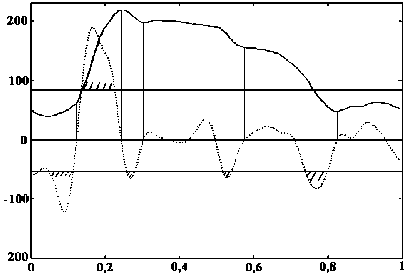
Рис. 14. Результаты обработки динамограммы (определение границ участков)

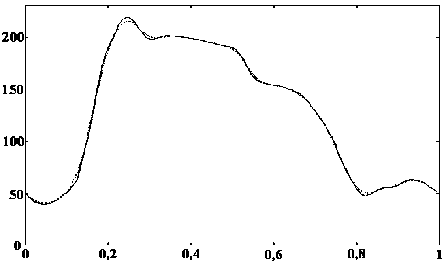
Рис. 15. Исходная и усредненная динамограммы