Определение характеристик ИНЧ-волн, наиболее сильно реагирующих на незначительные изменения электронной плотности ионосферы в области высоких широт

Одними из основных задач радиофизики в области распространения электромагнитных сигналов в атмосфере Земли являются поиск методов обеспечения стабильной связи или радиолокации на различных частотах; определение условий, когда эта связь невозможна; прогнозирование исключения таких условий и поиск мешающих связи или радиолокации факторов. Диагностика D-области ионосферы важна для многих физических приложений. В настоящее время основным отработанным средством такой диагностики являются радары частичных отражений. Ионозонды и радары некогерентного рассеяния формально захватывают D-область, но имеют там точность хуже, чем радары частичных отражений [Акимов, Калинин, 2017] . Состояние D-слоя ионосферы влияет на характеристики электромагнитных сигналов в диапазонах ИНЧ (0.3–3 кГц) и ОНЧ (3–30 кГц). Однако остается вопрос извлечения максимального количества информации о состоянии D-слоя из наземных измерений электромагнитных сигналов в указанном диапазоне.

В работе с помощью численного моделирования изучается влияние небольших (3–5 %) изменений концентрации электронов в D-слое ионосферы на характеристики электромагнитного сигнала на частоте 1500 Гц. Небольшие изменения концентрации электронов выбраны авторами с целью определения границ возможности диагностики D-слоя ионосферы сигналами ИНЧ-диапазона. Показано, что эти изменения не влияют на амплитуду отдельных компонент электромагнитного поля сигнала на уровне поверхности Земли, оказывают незначительное влияние на отношение амплитуд напряженностей электрического и магнитного полей и заметное влияние на разность фаз между напряженностями электрического и магнитного полей. Также исследовано влияние горизонтальных размеров области повышенной концентрации на перечисленные характеристики сигнала.

Для численного моделирования распространения сигналов ИНЧ-диапазона авторы использовали ранее разработанную ими модель распространения электромагнитных сигналов в системе литосфера— атмосфера—ионосфера. В модели численно интегрируется по времени система уравнений Максвелла на регулярной пространственной сетке. Для этого используется явная схема расщепления по пространственным направлениям и физическим процессам с противопотоковой аппроксимацией пространственных производных (метод Годунова с коррекцией потоков). Эта схема является консервативной, монотонной, имеет второй порядок точности по времени и третий по пространственным переменным.

В представленных численных экспериментах авторы используют прямоугольную область моделирования и декартову систему координат, пренебрегая кривизной сферических слоев литосферы, атмосферы и ионосферы по следующим причинам. Наибольший из горизонтальных размеров области моделирования примерно в шесть раз меньше радиуса Земли, а длина волны (~200 км) сравнима с размерами области моделирования. При таком соотношении масштабов сигнал распространяется горизонтально без многократных отражений от ионосферы и литосферы. Целью моделирования является исследование влияния локальных неоднородностей концентрации электронов в D-области ионосферы на характеристики электромагнитного сигнала. Плоская геометрия области моделирования для всех представленных численных экспериментов будет давать одинаковую малую ошибку, которая не окажет влияния на обсуждаемые закономерности в характеристиках сигнала.

ПОСТАНОВКА ЗАДАЧИ И ЗАДАНИЕ СРЕДЫ

В представленной работе авторы подробно рассматривают влияние незначительного повышения электронной плотности в нижней ионосфере в области высоких широт на прохождение электромагнитных волн ИНЧ-диапазона при различной конфигурации горизонтальных профилей электронной концентрации. Параметры среды задавались следующим образом: концентрация нейтральных частиц — с помощью эмпирической модели NRLMSISE-00; концентрация и температура электронов — с помощью эмпирической модели IRI 2016 с коррекцией по записям средневолнового радиолокатора вертикального излучения для исследования нижней ионосферы, расположенного на радиофизическом полигоне «Туманный» Полярного геофизического института в Мурманской области (69.0° N, 35.7° E) [Терещенко и др., 2003] , во время и после солнечной вспышки 15.03.2013, а именно 15.03.2013 в 09:00 UT (возмущенные условия, вспышка), 16.03.2013 в 09:00 UT (спокойные условия), 17.03.2013 в 06:00 UT (возмущенные условия, магнитная буря) и 16.03.2013 в 06:00 UT (спокойные условия). Вертикальные профили электронной плотности в указанных условиях показаны на рис. 1. Коррекция заключалась в перенесении тонкой структуры D- и E-областей, полученной по данным радиолокатора, на профили, полученные с помощью эмпирических моделей IRI 2016 и NRLMSISE.

Магнитная буря 17 марта 2013 г. была вызвана солнечной вспышкой М-класса 15 марта и началась с приходом к магнитосфере межпланетной ударной волны, которая проявилась на земной поверхности

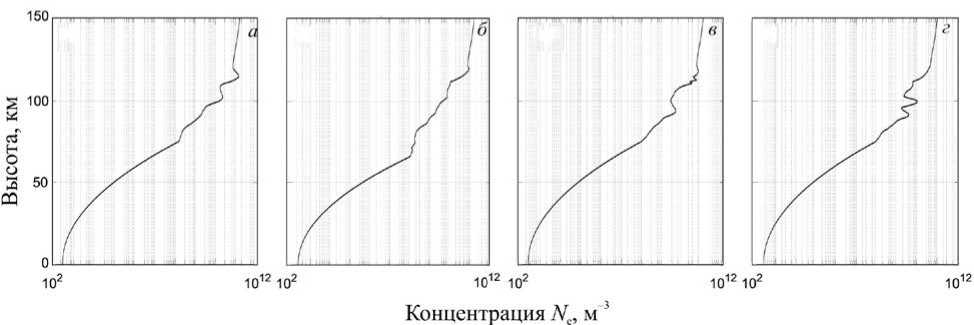
Рис. 1. Аппроксимированные высотные профили концентрации электронов 15.03.2013 в 09:00 UT ( а ); 16.03.2013 в 09:00 UT ( б ); 17.03.2013 в 06:00 UT ( в ) и 16.03.2013 в 06:00 UT ( г )

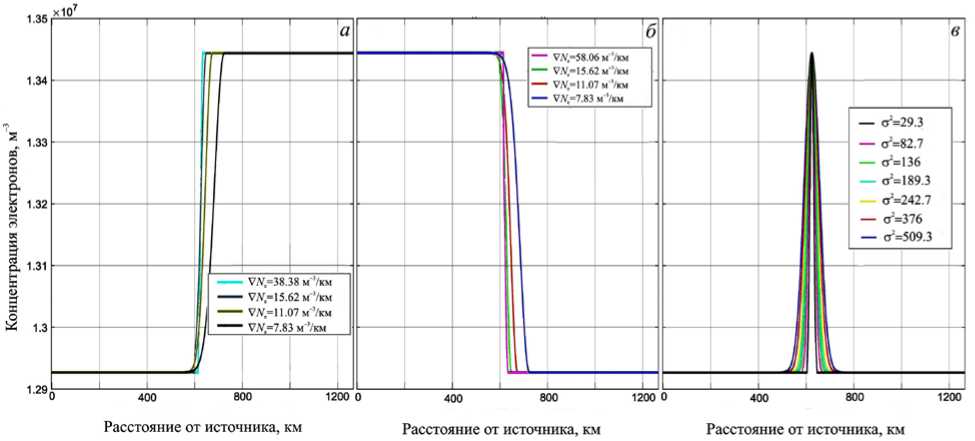
Рис. 2. Горизонтальные профили концентрации электронов для эксперимента по распространению электромагнитной волны из спокойной области в возмущенную ( а ); из возмущенной области в спокойную ( б ); сквозь полосу повышенной концентрации электронов ( в )

в виде SSC (sudden storm commencement) в 06:00 UT. В этот момент скорость солнечного ветра резко увеличилась с ~400 до ~650–700 км/с, B z -компонента ММП стала отрицательной, что обеспечило постоянное поступление энергии в магнитосферу. Индекс SYM-H , характеризующий интенсивность магнитной бури, упал до –100 нТл и оставался на этом уровне. Авроральный AE -индекс резко возрос до ~1000 нТл и оставался повышенным. АЕ -индекс показывал в 16:00 UT появление другой авроральной активизации (увеличение AE до ~2500 нТл).

Несмотря на высокий класс вспышки, радар частичных отражений на полигоне «Туманный» и модель IRI показали незначительное повышение концентрации электронов на высотах D–E-областей ионосферы во время последующей магнитной бури. Авторы полагают, что такие условия хорошо подходят для разделения технически наблюдаемых и ненаблюдаемых характеристик электромагнитных волн и выделения тех из них, которые могут быть использованы для создания методов косвенных исследований ионосферы.

Профиль проводимости литосферы был взят из работы [Korja et al., 2002] , проводимость у поверхности составляла 2∙10^–5 См.

Пространственная горизонтальная структура электронной плотности тоже может оказывать влияние на получаемые результаты. Для обнаружения этого влияния были проведены три серии экспериментов с горизонтальными профилями электронной плотности разных типов. Первая серия моделирует переход из спокойной области в область повышенной концентрации электронов. Горизонтальный профиль электронной концентрации показан на рис. 2, а. Вторая серия моделирует переход из области повышенной концентрации в спокойную область (профиль на рис. 2, б). Третья серия — прохождение полосы повышенной концентрации (рис. 2, в). Для всех серий переход осуществлялся по функции Гаусса. При этом в первых двух изменялся горизонтальный градиент для обнаружения его влияния в области перехода на распространение электромагнитных волн, в третьей изменялась ширина полосы с 0.25λ до λ, где λ — длина волны. Магнитное поле было взято вертикальным, что характерно для высоких широт, его индукция составляла 5.3^10-5 нТл.

ОБЛАСТЬ МОДЕЛИРОВАНИЯ, ПРОСТРАНСТВЕННАЯ СЕТКА И ИСТОЧНИК СИГНАЛА

Во всех поставленных в работе численных экспериментах область моделирования представляла собой параллелепипед с основанием 512x1280 км, высотой в атмосфере 150 км и глубиной в литосфере 50 км. Шаги сетки по горизонтали составляли 2 км, по вертикали в атмосфере 2 км и 0.5 км в литосфере. Шаг интегрирования по времени составлял 4^10-6 с.

На всех границах области моделирования применялись специальные условия свободного ухода волны для минимизации влияния нефизических отражений на результаты моделирования. Авторы применяли для моделирования постоянно действующий гармонический источник сигнала, а результаты анализировались при прекращении всех процессов, связанных с прохождением первичного фронта сигнала (35-й период колебаний). Поэтому, несмотря на почти 100 % отражение сигнала от высокопроводящих литосферы и ионосферы, находящихся внутри области моделирования, для исключения любой возможности накопления ошибок на вертикальных гранях расчетной области применялись такие же условия, как и на горизонтальных.

В качестве источника сигнала во всех представленных экспериментах используется поверхность одной из граней расчетной области. Такой источник сигнала позволяет задать не только амплитуду сигнала во времени, но и ее распределение в пространстве; задержками можно сформировать фронт волны необходимой формы подобно тому, как это делается в плоской эквидистантной фазированной антенной решетке [Воскресенский и др., 2012] . В экспериментах, обсуждаемых в данной работе, моделировалась плоская волна частотой 1500 Гц (длина волны ~200 км), излучаемая в область под прямым углом к плоскости источника.

ОПИСАНИЕ МОДЕЛИ

Используемая в представленной работе модель распространения электромагнитных сигналов в волноводе Земля—ионосфера с учетом инерции электронов в ионосфере построена на численном интегрировании по времени системы уравнений Максвелла на регулярной пространственной сетке с помощью явной схемы. Используется расщепление по пространственным направлениям и по физическим процессам. В схеме чередуются шаги распространения по каждому направлению и шаги затухания и вращения электрического поля сигнала. Также на шагах распространения по пространственным направлениям используется противопотоковая аппроксимация пространственных производных (метод Годунова с коррекцией потоков). Схема является консервативной, монотонной, имеет второй порядок точности по времени и третий по пространственным переменным.

Схема численного интегрирования уравнений Максвелла в литосфере

Пусть r =( x , y , z ) — декартовы координаты; t — время; E ( r , t ), D ( r , t ), H ( r , t ) и B ( r , t ) — напряженность и индукция электрического и магнитного полей; j ( r , t ) — плотность тока в момент времени t в точке с радиус-вектором г . Рассмотрим уравнение Фарадея и уравнение Максвелла в системе СИ

^ B = - rot E ( r , t ), ^ D = rot H ( r , t ) - j ( r , t ).       (1)

о t                  d t

В литосфере эти уравнения замыкаются законом Ома в форме

^{j (} r , t ) = о ( г ) Е ( г , t ),

где o( r ) — скалярная проводимость среды, и материальными уравнениями

D ( r , t ) = S o S ( r ) E ( r , t ), B ( r , t ) = P 0 P ( r ) H ( r , t ), (3)

где e(r) и p(r) — безразмерные относительные ди- электрическая и магнитная проницаемости среды в низкочастотном пределе; е0 и р0 — электрическая и магнитная проницаемости вакуума.

В представленных расчетах мы полагали, что в литосфере p( r )=1, однако мы сохраним р в дальнейших формулах, поскольку используемая методика позволяет рассматривать общий случай с переменной p( r ).

Пусть c ₀ = 1/ ^ £ ₀ p ₀ — скорость света в вакууме;

c(r) = c0 / V£(r)p(r) — скорость света в среде в точке с радиус-вектором r. Систему (1)-(3) можно записать в виде ав         dE  c2 +

= -rotE,    = -rot д t            д t    £

B

Ц

- —E.

^£ 0 ^£

Для численного интегрирования системы (4) применим метод расщепления по физическим процессам. Общий шаг интегрирования разделяется на два подшага. Один из них — это подшаг распространения, на котором интегрируется система уравнений dB д t

dE  с22

=-rotE,     = —rot II dt    £(pj

второй — подшаг затухания сигнала, на котором аналитически интегрируется система уравнений dE _

--=--E dt£ по формулам E(r, t + t) = E(r, t) exp I -       I. Пра-

( £0£(r)J вильное чередование подшагов расщепления обеспечивает второй порядок точности по времени.

Рассмотрим численное интегрирование системы

(5). Введем перенормированные поля

B(r, t) = c0B(r, t), E(r, t) = c0 / c(r)E(r, t), а также вектор M(r) = Vc в представленных расчетах, равный M(r) = Vc + cVц(r)/ ц(г) в общем случае. Умножая уравнение Фарадея на c0, получим уравнение

• 8    В

— = - rot(c E ).                               (6)

• 8    t

Подстановка введенных обозначений в уравнение Максвелла приводит это уравнение к виду dE = rot ( c — )-[m X — ].

Введем матрицы Rx, Ry, Rz и нулевую мат- рицу O:

	" 0 0	0 )		f 0 0 1 )
R + =	0 0	- 1	, R У =	0 0 0
	+ 0 1	0 у		+- 1 0 0 ,
	' 0 - 1	0'		f 0 0 0 )
R z =	1   0	0	, O =	0 0 0 .
	+ 0 0	0		+ 0 0 0 v

Оператор rot в декартовых координатах можно представить в виде

• da     da

rota = Rx — + Ry — + Rz —.

8x     dy

Введем шестимерные вектор-столбец переменных u = ( B x , B y , B z , E x , E y , E z ) T и вектор F = ( F , F ₂, F ₃, F ₄, F ₅, F ₆ ) T , компоненты которого заданы формулами

F j = F ₂ = F 3 = 0, ( F 4 , F 5 , F 6 ) T = -[ m x — ] . (10)

Используя обозначения (8), а также формулы (9) и (10), систему уравнений (6), (7) можно представить в виде векторного уравнения du     d(cu)      d(cu)     d( cu)

+ A x      + A y      + A z      = F ,     (11)

8t       8x        dy        8z где Ax, Ay, Az — симметричные матрицы размером 6X6, заданные формулами

^

A x

O R x

(- R x O )

^

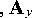
О ^R y

(- R y O J

^

A z

'•> ^,

O R z

(- R z O J

Векторное уравнение (11) задает шестимерную линейную гиперболическую систему уравнений первого порядка, записанную в консервативной форме. Ее правая часть F линейно зависит от компонент вектора u. Для численного интегрирования таких систем разработано достаточно много разностных схем, в том числе схемы повышенного порядка точности, которые применяются для уравнений газовой динамики. Наиболее полное описание этих схем содержится в монографиях [Куликовский и др., 2012; Бисикало и др., 2013].

Используя метод расщепления по пространственным направлениям, можно построить явные монотонные схемы численного интегрирования системы (11), которые сводятся к последовательному интегрированию одномерных по пространству гиперболических систем уравнений. На каждом временном шаге нужно последовательно проинтегрировать три системы уравнений, например в таком порядке:

d u '      d ( c u )

+ A x— 8 t         8 x

= F , ^ A , ^ = f , ^x 8 t           8 y       y

d u^m

---+

8 t

A z

d ( c "') = F d z       ^z

При этом правые части систем (13) выбираются так, чтобы они не изменялись на своем шаге расщепления и удовлетворяли равенству

F = F x + F y + F z .

Эти условия будут выполнены, если задать их по формулам

T

0,0,0,0, - MB. , mb \ , zx yx

T

0,0,0, - M z B y ,0, - M x B y ) ,

T

0,0,0, - M y B z , M x B z ,0 ) .

На каждом шаге расщепления для двух компонент магнитного поля и двух компонент электрического поля, ортогональных направлению шага, рассчитывается распространение сигнала конечно-разностным способом. В качестве начальных условий для каждой системы уравнений в (13) берутся значения, рассчитанные на предыдущем шаге расщепления. Сохранить второй порядок аппроксимации по времени в схеме расщепления можно, если циклически изменять порядок выполнения шагов расщепления, например, выполняя сначала шаги по пространственным направлениям в следующем порядке: xyz , yxz , zxy , xzy , yzx , zyx . Обоснование этого утверждения содержится, например, в монографиях [Бисикало и др., 2013; Ковеня и др., 1981] .

Пусть заданы равномерная сетка по времени tn=10+nт, где т — шаг по времени, и равномерная пространственная сетка в декартовых координатах, целые и полуцелые узлы которых заданы соотношениями x = x0 + hxx, y, = y 0 + jhy , zk = z 0 + khz, r, j, k =( x,, y,, zk), xi+1/2 = x0 + (i + 1Z 2) hx, y,+1/2 = y0 + (j + 1Z 2) hy , zk+1/2 = z 0 +( k + 1/2) hz , в которых hx, hy, hz — шаги сетки по осям X, Y, Z соответственно. Будем использовать для значений функции f в узлах сетки обозначения f (rj,k, tn) = f ”,,k.

Рассмотрим послойный переход для первой системы из (13), которая интегрируется на шаге расщепления по направлению х . В этом случае представим заданную первой формулой в (10) матрицу

Ax в виде Ax = QЛQ , где Л — диагональная матрица, на диагонали которой стоят собственные числа матрицы Ax; Q — матрица, столбцы которой есть правые собственные векторы матрицы Ax, опре

- 1

деленные с точностью до множителя; Q — матрица, обратная Q. Строки матрицы Q 1 — левые соб ственные векторы матрицы Ax. Эти матрицы постоянны. Их можно взять в виде

( 0 0 0 0 0 0 )

0 1 0 0 0 0

Л =

0 - 1 0 0

0 0 0 0

0 0 0 0 1 0

( 0 0

0 0

⁰ - 1 )

(1    0   0 0   00

0 1/2 0   00 1/2

0   0  1/2  0  1/20

0   0   0  1   00

0   0 -1/2  0  1/20

( 0 - 1/2

0 0

0 1/2 )

0 0 0

0 0 ^

0 1 0 0

0 - 1

-•---1

Q

0 0

0 0

0 0

. 0 1

1 0 - 1 0

0 1

0 0

1 0 1 0

0 0 0

С помощью введенных матриц Л , Q и Q 1 первую систему уравнений в (13) представим в виде векторного уравнения

1 д ( c u ) д x

du '"

+ Q Л Q д t

= F x .

Введем вектор-столбец характеристических переменных (линеаризованные инварианты Римана)

1 по направлению x , заданный формулой w = Q u .

Компоненты вектора w заданы формулами

—-—~—•■                   -"^—^ '•—~—^                  .--——^ --—^—■ w1 Bx , w2 = By - Ez , w3 = Bz - Ey , w4 = Ex, w5 = Bz + Ey , w6 = By + Ez .

- 1

Умножим уравнение (15) слева на матрицу Q .

В результате получим векторное уравнение

^ w + Л ^w = Q - 1 F ,                  (16)

д t       дx         x которое является системой из шести скалярных уравнений для характеристических переменных.

В итоге численное интегрирование первой системы из (13) сводится к численному интегрированию четырех независимых одномерных по пространству уравнений переноса (16) для характеристических переменных w2 = By - Ez , w3 = Bz - Ey , w5 = Bz + Ey, w6 = By + Ez .

Это интегрирование выполняется с помощью явной противопотоковой схемы, имеющей третий порядок точности по пространству и второй — по времени. Эта схема подробно описана в работах [Мингалев и др., 2018а, б] .

Рассмотрим кратко основные идеи, лежащие в основе численной схемы.

Схема численного интегрирования уравнений Максвелла в ионосфере

Для ионосферы мы полагали, что безразмерная относительная магнитная проницаемость среды p ( r ) = 1 и выполняется формула B ( r , t ) = ц ₀ H ( r , t ). Также мы полагали, что имеет место поляризация плазмы D ( r , t ) = s ₀ E ( r , t ) + P ( r , t ), где P ( r , t ) — вектор поляризации, причем плотность тока поляризации д Р / д t = j совпадает с полной плотностью тока в плазме. Уравнение Фарадея и уравнение Максвелла в этом случае принимают вид

— = - rot E , — = c ₀'rot B - — j .             (17)

д t , д t     ⁰          s ₀

Система (17) замыкается уравнением для плотности тока электронов, вызванного полем сигнала:

fj =- V ej -^e [ jX b^ro^E, д t где ve — частота столкновений электронов, Qe = e |Ввн| / me — гирочастота электронов, Ввн — внешнее геомагнитное поле, b = B / B , вн вн

® 2 = e 2 n e / ( m e e ₀ ) — квадрат плазменной частоты электронов.

В ионосфере, как и в литосфере, применяется метод расщепления по физическим процессам. Правильное чередование подшагов расщепления обеспечивает второй порядок точности по времени. На подшаге распространения учитывается только распространение сигнала и численно интегрируется система уравнений

^ B = - rot E , — = c 2² rot B                     (18)

д t             д t     ⁰

с помощью той же схемы, что и система (5) в литосфере.

На подшаге затухания и вращения сигнала магнитное поле сигнала не изменяется и учитываются только затухание электрического поля и его вращение за счет внешнего геомагнитного поля. При этом в каждой точке расчетной сетки аналитически интегрируется система уравнений

| E = - — j,    = - V e j a [ ^{j X b} ] + ro 2 S o ^E .

д t ^ o    д t

Эта система разделяется на две независимых системы для продольных электрического поля E = ^{( b} , ^{j )} и тока j\ = ^{( b} , ^{j )}

d E     2 . d j _     2

, =      j\\ , — = - ^V e j\\ + ® e ^E 0 ^E ||                ⁽²⁰⁾

dt      Eo dt и поперечных электрического поля E± — E - bЕц и тока L = j — bj|| :

dE± = _2 • dt      Eo

± ,

^ j T = - ^V e ^j ± - ^Q e [ ^{L X} b ] + ® ² e 0 ^E ± .

d t

Системы (20) и (21) являются автономными линейными системами однородных дифференциальных уравнений (ОДУ) с постоянными коэффициентами. Решения задачи Коши для этих систем выражаются достаточно громоздкими аналитическими формулами.

В той части ионосферы, где выполнено неравенство ve t> 20, системы (20) и (21) заменяются на более простые уравнения и систему, дЕ\ д t

—

² ® 2_F

—Е\\

v _e

5 E _± _ 2 ® 2 v _e д t      v 2 + Q 2

E _± — ^^ [ E _± x b ] ^v

которые также имеют аналитические решения задачи Коши.

Изложенная схема позволяет учесть частотную дисперсию и моделировать распространение широкополосных сигналов произвольной формы.

Условия на границе области моделирования

В модельных экспериментах на всех внешних границах было задано граничное условие свободного ухода волны, что достигалось обнулением входящего из-за пределов области моделирования потока. Такой подход позволяет получить низкие коэффициенты отражения плоской волны от границ области моделирования: для волн, падающих под углом от 80° до 90°, отношение амплитуды отраженной волны к амплитуде падающей плоской волны не превышает 0.01. При угле падения 60° это отношение составляет уже ~0.05, при угле 45° — ~0.16, при угле 27° — ~0.33, а при угле 18.4° — ~0.43 [Мингалев и др., 2018а]. Для сравнения: метод FDTD (finite-differences time-domain method) [Yee, 1966] при применении простых граничных условий, таких как условия Мура [Mur, 1981] и Лиао [Liao, 1984], дает отражения порядка 0.1…1 %, но только при падении волны на границу под прямым углом. При падении под острым углом коэффициент отражения растет до 100 % при падении по касательной. Однако при использовании непрерывно действующего источника даже столь малых отражений, которые порождает применяемая схема, достаточно для накопления ошибок в области моделирования, поэтому возникает необходимость использования методов подавления, подобных PML (perfectly matched layer), использующихся в FDTD-моделях [Berenger, 1994]. Именно такой тип источника применялся в представленных авторами экспериментах, что привело к необходимости адаптации и применения метода PML. Разделение схемы по пространственным переменным и физическим процессам позволяет применять профиль электрических и магнитных потерь, предложенный Беренгером, непосредственно к потокам противопотоковой схемы на границе области моделирования. Геометрический профиль потерь внутри отдельного слоя имеет вид

Р ( r) = — ^° c 0 ln⁽ g )n ln( R o ) g* r / " ^ ) , (22) 2 A x ( g ^N — 1)

где g — коэффициент геометрической прогрессии; Δ x — шаг по пространству; c 0 — скорость света; N — номер PML-слоя, считая от интерфейса счетного региона и границы; r — расстояние от границы; R 0 — коэффициент отражения от первого слоя. В представленных численных экспериментах авторы используют профиль потерь, рассчитанный по формуле (22) со следующими параметрами: R 0 =0.01 (1 %), коэффициент прогрессии g =2.15, количество слоев 14. Несмотря на то, что коэффициент отражения от первого слоя не меньше, чем характерный для данной схемы при обнулении исходящих потоков на углах падения 80°–90°, а на практике даже больше вследствие отражений от последующих слоев, основным преимуществом метода PML является его крайне слабая зависимость от угла прихода электромагнитной волны. Данную особенность демонстрирует и адаптированный для противопотоковой схемы вариант.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Авторами были проведены численные эксперименты семи типов: четыре эксперимента — с модельной областью, однородной по горизонтали и вертикальными профилями электронной плотности, как на рис. 1; три серии экспериментов — с переходом в направлении распространения волны, представленные на рис. 2. Модельный сигнал, исследуемый для всех представленных в работе численных экспериментов, задавался синусоидальной функцией с частотой 1500 Гц. Авторы не обсуждают переходные процессы, связанные с началом счета и прохождением фронта волны через области с не нулевым горизонтальным градиентом концентрации электронов. Все обсуждаемые далее результаты получены для устоявшегося режима (30-й –35-й периоды колебаний от начала моделирования). В связи с этим анализировать непосредственно временные формы компонент электромагнитного сигнала нецелесообразно, так как они идентичны исходному сигналу. Далее авторы сравнивают и обсуждают отдельные характеристики электромагнитного сигнала, такие как амплитуда и фаза, а также их производные.

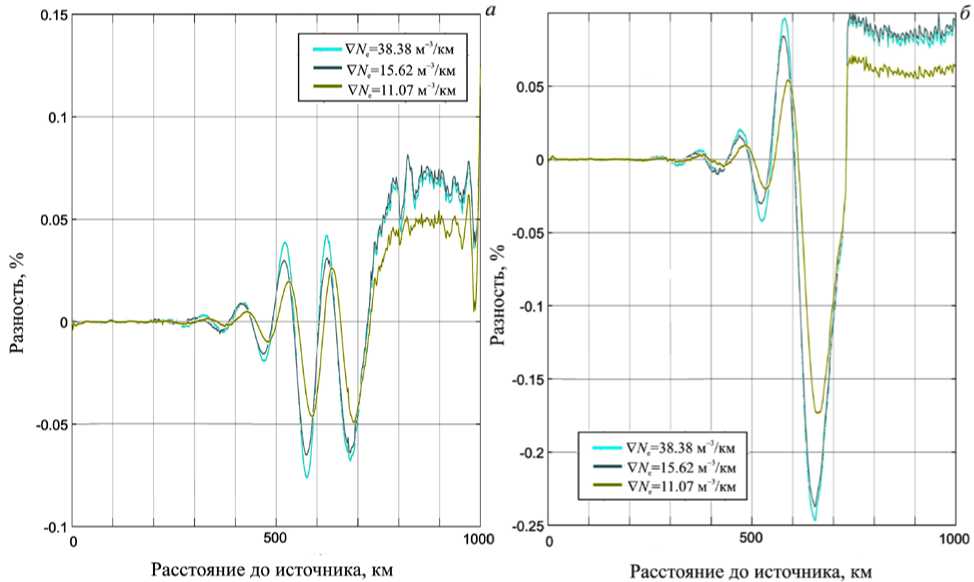
Рис. 3. Разность амплитуд в процентах для электрического ( а ) и магнитного полей ( б ) для случаев распространения сигнала, когда вся область имела профиль электронной концентрации, характерный для спокойных условий 16.03.2013 в 06:00 UT и когда горизонтальный профиль концентрации электронов имел переход из спокойной области в область с повышенной концентрацией электронов

На рис. 3, а изображена разность амплитуд в процентах основной компоненты электрического поля волны для случаев распространения сигнала, когда вся область имела профиль электронной концентрации, характерный для спокойных условий 16.03.2013 в 06:00 UT и когда горизонтальный профиль концентрации электронов имел переход из спокойной области в область с повышенной концентрацией электронов, которая имела профиль, характерный для условий магнитной бури 17.03.2013 в 06:00 UT. На рис. 3, б изображена разность амплитуд основной компоненты магнитного поля волны в тех же экспериментах. На рис. 4, а , б изображена разность амплитуд основной компоненты электрического и магнитного полей волны для случаев распространения сигнала, когда вся область имела профиль электронной концентрации, характерный для условий магнитной бури 17.03.2013 в 06:00 UT и когда горизонтальный профиль концентрации электронов имел переход из области с повышенной концентрацией электронов в спокойную область, которая имела профиль, характерный для 16.03.2013, 06:00 UT. Видно, что распространение через области как положительного, так и отрицательного горизонтального градиентов электронной плотности оказывает влияние на амплитудные характеристики электромагнитных волн тем сильнее, чем выше градиент в области перехода. Однако в случае слабых возмущений электронной плотности изменения амплитуд основных компонент электромагнитного поля не достаточны для регистрации методами наземных наблюдений.

Анализ прохождения электромагнитной волной полосы повышенной концентрации электронов, расположенной перпендикулярно направлению распространения и параллельно плоскости волны, не выявил значительного влияния на амплитудные характеристики сигнала, независимо от соотношения ширины полосы и длины волны. Очевидно, что отдельная регистрация компонент электромагнитного поля не может быть использована для анализа слабых возмущений концентрации электронов в ионосфере, так как амплитудный отклик на них не превышает значений фонового шума.

Ситуация несколько улучшается в случае совместного анализа электрических и магнитных компонент электромагнитного поля. На рис. 5 показаны графики волнового сопротивления среды, рассчитываемого как отношение напряженностей магнитного и электрического полей для случаев горизонтально однородной среды с вертикальными профилями всех типов, представленных на рис. 1, и для случаев прохождения полосы повышенной концентрации электронов шириной λ и 0.25λ. Видно, что такой подход позволяет достаточно четко отделять случаи с наличием областей возмущений электронной плотности в ионосфере на радиотрассе от случаев спокойных условий, но слабо реагирует как на величину возмущений электронной плотности, так и на горизонтальную структуру данных возмущений. Для реализации данного подхода при анализе данных регистрирующая аппаратура в случае плоской волны, распространяющейся в плоскости волновода Земля—ионосфера, должна позволять фиксировать

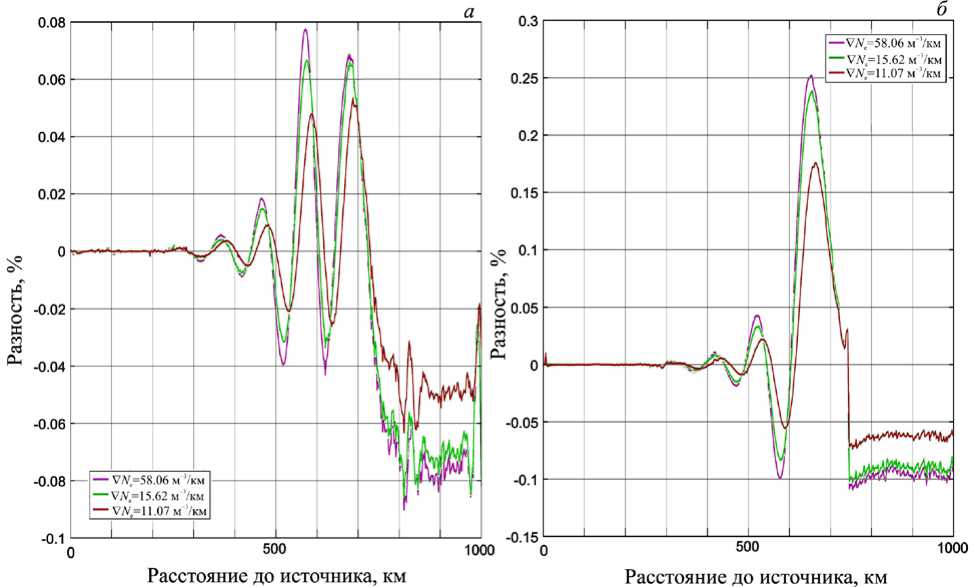
Рис. 4. Разность амплитуд в процентах для случаев распространения сигнала, когда вся область имела профиль электронной концентрации условий магнитной бури 17.03.2013 в 06:00 UT и когда горизонтальный профиль концентрации электронов имел переход из области с повышенной концентрацией электронов в спокойную область: а — напряженность электрического поля; б — напряженность магнитного поля

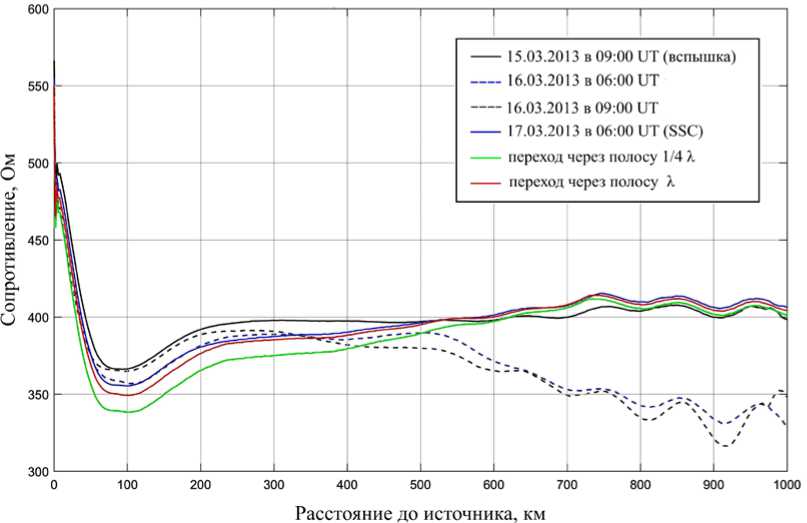
Рис. 5. Волновое сопротивление среды

вертикальную компоненту электрического поля и две горизонтальные компоненты магнитного поля. В случае волн другого типа или произвольного направления распространения необходима фиксация всех шести компонент электромагнитного поля.

На рис. 6 показаны разности фаз напряженностей магнитного и электрического полей для случаев горизонтально однородной среды с вертикальными профилями всех типов, представленными на рис. 1, и для случаев прохождения полосы повышенной концентрации электронов шириной λ и 0.25λ. Видно, что фазовые характеристики наиболее сильно дифференцированы в зависимости от величины возмущения электронной плотности как в случае изменения вертикального профиля концентрации электронов, так и в случае горизонтального профиля в сравнении с ранее рассмотренными. Очевидно, что остается неопределенность, какого типа возмущение выз-

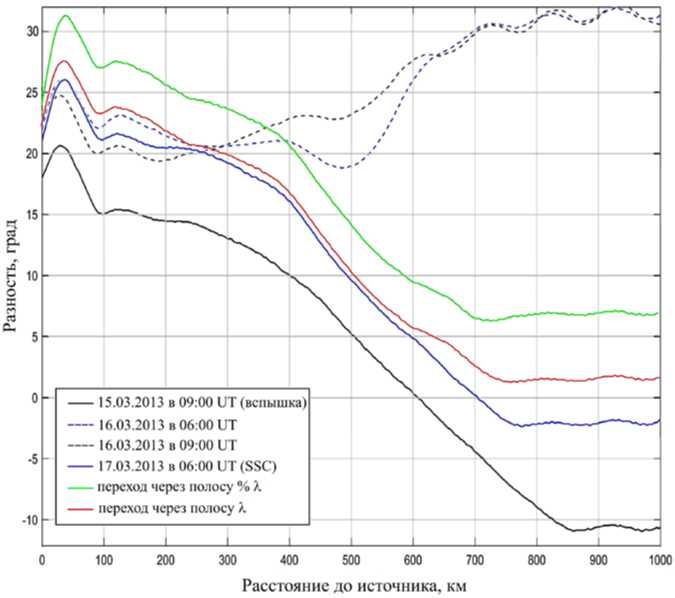
Рис. 6. Разность фаз между напряженностями электрического и магнитного полей

вало изменение фазы в каждом конкретном случае. Также остается вопрос зависимости сдвига фазы от формы профиля электронной концентрации, а также ее величины для волн различных диапазонов. Эти и многие другие вопросы требуют дополнительной проработки, выходящей за рамки представленной работы.

Для проведения анализа фазовых характеристик необходимо при регистрации компонент электромагнитного поля осуществлять точную привязку по времени регистрируемых электрических и магнитных компонент. В случае создания сети приемников, что может помочь с идентификацией горизонтальных ионосферных неоднородностей, необходимо обеспечить точную привязку по времени регистрируемых компонент поля к мировому времени, как, например, это делается в работе [Пильгаев и др., 2008] .

ЗАКЛЮЧЕНИЕ

Методами численного эксперимента авторами выполнена задача определения характеристик электромагнитных волн ИНЧ-диапазона, регистрируемых на уровне приземного слоя, несущих максимальное количество информации о состоянии волновода Земля—ионосфера.

Выявлено влияние горизонтальных градиентов концентрации электронов на амплитуду электромагнитных сигналов ИНЧ-диапазона при переходе между областями с различными характеристиками волновода Земля—ионосфера. Показано, что в случае незначительных изменений электронной плотности изменения амплитуды электромагнитного сигнала незначительны и не превышают 1 %.

Выявлено существенное влияние вида вертикального профиля электронной концентрации на волновое сопротивление среды и разность фаз между магнитной и электрической компонентами. Показано, что в случаях увеличения концентрации электронов в D-области волновое сопротивление среды увеличивается, а компонента электромагнитного поля E начинает запаздывать относительно H . По мнению авторов, отставание фазы электрического поля от магнитного обусловлено инерцией электронов и их столкновениями с нейтральными частицами ионосферы. Вызванная электрическим полем сигнала плотность электрического тока влияет на сдвиг фаз между моментами достижения максимальных значений электрическим и магнитным полями сигнала в фиксированной точке ионосферы.

На основании проведенных расчетов можно сделать вывод, что минимально пригодные для мониторинга состояния ионосферы наземные системы регистрации ИНЧ-волн должны содержать в своем составе три регистратора: один для вертикальной электрической компоненты и два для горизонтальных магнитных компонент электромагнитного поля. При этом важно обеспечить качественную синхронизацию между регистраторами и мировым временем.

Исследование выполнено при поддержке гранта Российского научного фонда (проект № 18-77-10018).