Определение характерных параметров СТМ-изображений наноструктур методом статистического анализа двумерных случайных полей

Предлагается алгоритм статистического анализа размеров элементов изображений, основанный на вычислении спектральной плотности изображения и являющийся реализацией цифрового подхода к решению обратной задачи. Возможности алгоритма продемонстрированы на примерах модельных изображений. Предложенный подход позволяет получить распределение элементов изображений по размерам. Приводятся результаты применения алгоритма при исследовании изображений полупроводниковых наноструктур, полученных в сканирующем туннельном микроскопе.

ОСНОВНЫЕ СООТНОШЕНИЯ

При исследовании полидисперсных сред оптическими методами анализируется интенсивность светового пучка, рассеянного мутной средой [1–4]. Развитый в этих работах подход используется нами в рамках статистического цифрового анализа двумерных случайных полей [5].

Для определения статистических характеристик размеров объектов на изображении предлагается применить цифровые методы анализа, рассматривая изображения как двумерные однородные случайные поля. При этом аналогом интенсивности рассеяния световых волн для различных углов отклонения является спектральная плотность изображения, вычисленная как квадрат модуля его дискретного двумерного преобразования Фурье. За основу исследования предлагается взять неупорядоченное двумерное поле, элементами которого являются диски со случайными радиусами a_i , центры которых расположены в точках r_i . Предполагается статистическая независимость случайных величин a_i и r_i , а также статистическая независимость расположения различных дисков. Для индикатрисы рассеяния света I_p ( θ ) в таком случае справедливо соотношение [1, 3]:

ю

I p (9 ) = I о 9 J _Ю ( р ) р ² J i² ( р9 ) dp ,       (1)

где I ₀ — интенсивность светового пучка в отсут-2 πa ствии рассеяния, 9 — угол рассеяния, р =--- ,

λ

λ — длина волны падающего света, ω(ρ) — плот- ность распределения по нормированным размерам, J1 — функция Бесселя первого рода.

Путем простых преобразований из выражения (1) можно получить соотношение, связывающее спектральную плотность изображения G ( f )и плотность распределения элементов изображения по размерам w ( a ) :

ю

G ( f ) = Cf - 2 J w ( a ) a 2 J 12 ( fa ) da ,       (1а)

где G(f ) — спектральная плотность исследуемого изображения, f — пространственная частота, f = V fX + /У , C — константа, a — радиус дисков, w(a) — плотность распределения радиусов дисков.

АЛГОРИТМ ЧИСЛЕННОГО РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ

Для получения плотности распределения радиусов дисков w ( a ) необходимо решить обратную задачу. Решение обратной задачи можно свести к решению линейной системы уравнений:

a i , k^xk = У , i , k = 1,™, n ,

A = [ a_ik ] — определитель матрицы коэффициентов этой системы.

Для определения существования решения предлагается нормировать эту систему, умножив каждое ее уравнение на

Gfi n ?^ )^-1

V    ^k - ¹       у

[4]. Наи-

лучшая обусловленность системы будет при A —± 1. Если определитель нормированной матрицы мал, то часто изменения элементов в пределах их точности обращают определитель в ноль. Это означает, что система уравнений в таком виде практически несовместна, и задача не имеет решений.

Другой способ решения обратной задачи в рассматриваемом случае основан на применении обобщенных интегральных преобразований и получении обратного по отношению к выражению (1а) преобразования [1]. В этом случае для плотности распределения по размерам имеем

г

w(a) = -—JfJ i(fa)N i(fa)—[f3G(f)—f, (2) a 0                 df где C1 — константа, N1 — функция Неймана первого рода.

Выражение (2) позволяет вычислить плотность распределения радиусов элементов двумерного случайного поля по его спектральной плотности. Сложность численного определения из соотношения (2) возникает из-за того, что под знаком интеграла находится производная от экспериментальной зависимости. В связи с этим встает задача сглаживания экспериментальной спектральной плотности G ( f )и получения гладкой производной, отражающей характер поведения зависимости f ³ G ( f ) , не связанный со случайными отклонениями спектральных компонент. Сглаживание предлагается проводить в три этапа. На первом этапе двумерная спектральная плотность изображения сглаживается с помощью двумерного спектрального окна W ( f_x , f_y ) , например окна Бартлетта:

G'(f., fy) = G (f., fy )**W (f., fy), где ** — операция свертки.

Так как приведенные выше соотношения получены для модели случайного поля со случайным образом расположенными круглыми дисками, то все направления на изображении равноценны, и двумерная спектральная плотность может быть усреднена по нескольким сечениям. Поэтому на втором этапе вычисляется

n

G "( f ) = - E G -( f ), n^

где    G ' _i ( f )   — i -е сечение функции

G '( f. , f, ), f — V f ⁺ fy" .

На третьем этапе предлагается осуществить сглаживание кривой G ''( f ) с помощью сплайнов.

После того как построена достаточно гладкая функция спектральной плотности, необходимо приближенно вычислить производную функции P ( fk ) = fk 3 G ( fk ), k = -,..., n . Для этого используется оператор первых разностей:

• —P ( f k ) P ( f k + 1 ) - P ( f k )   , ₉   „

— , k — 2 П .

• —f k         fk + i - fk

Таким образом, плотность распределения радиусов элементов изображения можно определить путем приближенного вычисления интеграла (2) для заданного набора величин радиусов a i , i — 1,..., m :

w(ai) — -AfC-EjJ-(fkai)N-(fkad dP^fk), (3) ai и                   fk где Af — интервал между соседними спектральными составляющими функции G''( fk) .

МОДЕЛЬНЫЙ ЭКСПЕРИМЕНТ

Эффективность описанного метода для вычисления плотности распределения размеров определялась на модельных случайных полях. Смоделированное изображение содержит элементы в виде дисков и рассматривается как конкретная реализация из совокупности изображений с заданными статистическими свойствами. Координаты центров дисков задаются с помощью генератора равномерно распределенных случайных величин. Радиусы дисков распределены по нормальному закону с заданными средним значением a ₀ и стандартным отклонением σ (рис. 1):

w 0 ( a ) — 1/(V2 n с т)exp( - ( a - a 0 )/2 ^ ²).

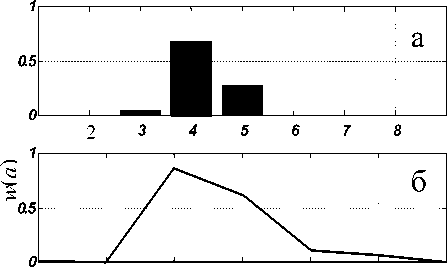
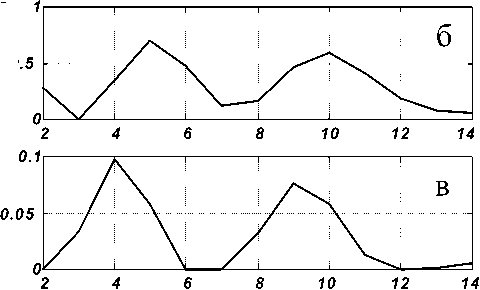
В процессе формирования множества элементов изображения с помощью генератора нормально распределенных случайных величин строится гистограмма величин радиусов дисков (рис. 2, а).

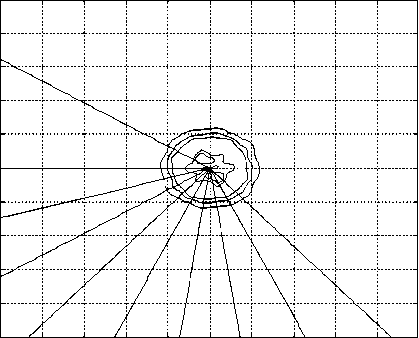
Для построенного изображения вычисляется спектральная плотность и выполняются процедуры ее сглаживания, по описанному выше алгоритму. Двумерная спектральная плотность модельного изображения, приведенного на рис. 1, изображена на рис. 3. Лучами показаны направления сечений, по которым проводилось усреднение спектральной плотности.

Для подтверждения адекватности предложенного алгоритма проводилось сравнение величины w ( a ) , полученной предложенным выше способом,

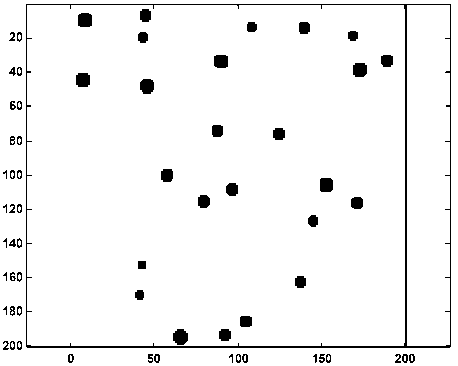
Рис. 1. Смоделированное изображение. Средний радиус диска 4 ед. Стандартное отклонение величины радиуса 1 ед.

0.4

0.3

0.2

0.1

-0.1

-0.2

-0.3

-0.4

-0.5

-0.5    -0.4   -0.3    -0.2   -0.1      0     0.1     0.2    0.3    0.4

Рис. 3. Двумерная спектральная плотность изображения, приведенного на рис. 1

0           50          100         150         200

Рис. 4. Смоделированное изображение для двухмодного распределения радиусов дисков: а = 4 и а = 9

a (радиус элемента)

Рис. 2. а. Гистограмма радиусов элементов изображения, приведенного на рис 1.

б. Результат вычислений по изображению.

в. Результат вычислений по рассчитанной спектральной плотности

с величиной w ₁ ( a ) , рассчитанной по такому же алгоритму. При этом в качестве G ( f ) в формуле (2) принималось решение прямой задачи (выражение 1а) с заданным при моделировании значением w ₀( a ).

Интеграл в формуле (1) вычисляется приближенно, по формуле прямоугольников:

m

G(f_k ) = Cf_k^x A a £ w ( a i ) a 2 J 2 ( f_ka_t ), i = 1

k = 1,..., n ,

где A a — интервал задания радиусов дисков, а остальные величины соответствуют формуле (1).

Результаты решения обратной задачи показаны на рис. 2: для экспериментальной кривой — на рис. 2, б, а для тестовой кривой — на рис. 2, в. Гистограмма величин радиусов смоделированного изображения (рис. 2, а) позволяет сравнить полученные результаты с данными об изображении.

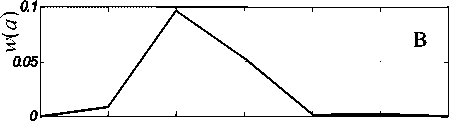
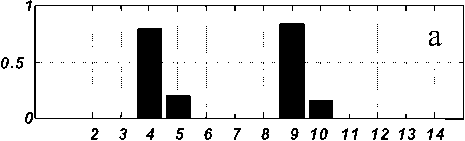
На рис. 4 и 5 представлены результаты обработки модельного изображения, содержащего элементы с двумя характерными размерами. Этот результат демонстрирует, что вычисления по формуле (2) дают в результате не просто средний размер элементов изображения, а именно плотность распределения радиусов элементов, которая может быть и двухмодовой (рис. 5).

(»> °     (»W

a (радиус элемента)

Рис. 5.

а. Гистограмма радиусов дисков на изображении рис. 8.

б, в. Результаты вычислений соответственно для изображения и тестовой спектральной плотности

Сравнение изображений, гистограмм и результатов вычислений позволяет сделать положительное заключение о корректности рассмотренного метода и предложить его для исследования реальных изображений.

ОБРАБОТКА СТМ-ИЗОБРАЖЕНИЙ

ПОЛУПРОВОДНИКОВЫХ НАНОСТРУКТУР

Данный алгоритм был исследован при определении характеристик размеров на СТМ- зображениях полупроводниковых наноструктур. Методом СТМ исследовались ансамбли квантовых очек (КТ), образующиеся в процессе самооргани-ации тонких полупроводниковых слоев при моле-улярно-пучковой эпитаксии [6]. Подобные нано-труктуры используются при создании твердотель-ых лазеров с рекордными параметрами, при этом арактеристики лазерного излучения определяются татистикой распределения размеров КТ [7]. На ис. 6 представлено СТМ-изображение ансамбля КТ. Обычно средние размеры КТ и их разброс оп-еделяются с помощью рутинной процедуры обра-отки многочисленных поперечных сечений СТМ-зображений (рис. 6, б).

Предложенный алгоритм позволяет в автомати-еском режиме получить необходимые количест-енные данные обо всем ансамбле КТ, обрабатывая днократно файл экспериментального изображе-ия. Вычисления по усредненному сечению спек-ральной плотности (рис. 7, а) позволяют получить плотность распределения радиусов квантовых точек w ( a ) , представленную на рис. 7, б. Нормированное распределение по размерам позволяет получить среднее значение радиусов элементов как:

N

R = ^ ^ ( a i )a i .

i = 1

Для определения средней плотности КТ на исследуемой поверхности предлагается вычислить среднюю площадь КТ ( S 1 ), аппроксимировав ее форму диск о м либо прямоугольником и используя значение R . Суммарная площадь, занимаемая всеми КТ ( S KT ), вычисляется по бинаризованному изображению, полученному в результате пороговой обработки. Тогда количество КТ на изображении можно определить как отношение

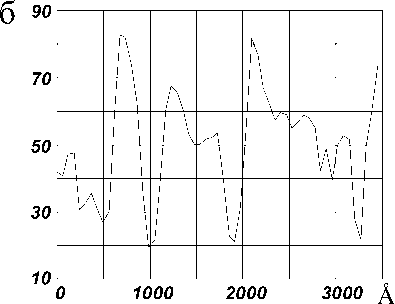
Рис. 6. а. Изображение гетероструктуры с квантовыми точками после медианной фильтрации и удаления трендов. Площадь сканирования 18 000 х 18 000 А. б. Сечение изображения

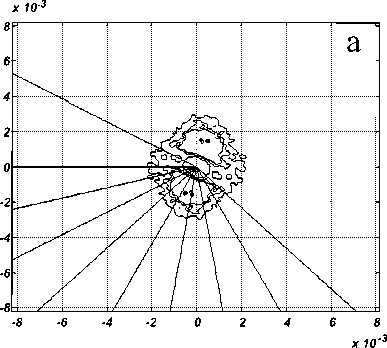
Рис. 7. а. Спектральная плотность изображения, представленного на рис. 6. б. Плотность распределения размеров квантовых точек

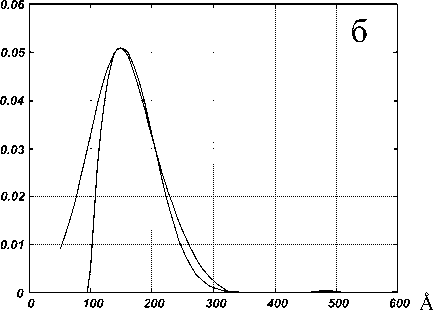
Рис. 8. СТМ-изображение ансамбля КТ, площадь сканирования 4000 х 4000 А

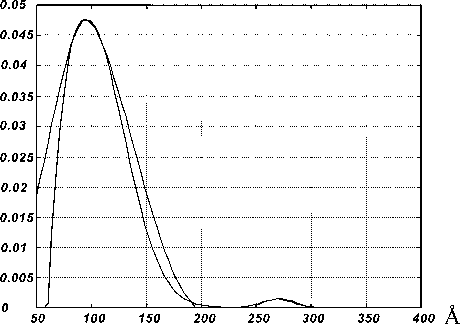
Рис. 9. Плотность распределения радиусов КТ, изображение которых дано на рис. 8

N = S KT-

KT    S1 , а среднюю плотность КТ на поверхности — N как р =-----, где SU3o6p — площадь сканирован-

S изобр ной поверхности.

На рис. 8 приведено СТМ-изображение ансамбля КТ, имеющих два характерных размера, что отражено на плотности распределения радиусов КТ, полученной по усредненному сечению, которая представлена на рис. 9. В результате аппроксимации этой кривой гауссовыми плотностями распределения получены значения характерных размеров КТ:

R 1 = 96 ± 34А, R 2 = 269 ± 14А,

R = 113А, средняя плотность расположения КТ на поверхности р = 826 мкм ^-1 .

Рассматриваемый способ вычислений справедлив для изотропных изображений. Не приводя строгих доказательств корректности, рассмотрим его применение при обработке неизотропных объектов, к которым относятся кристаллические структуры.

В этом случае вычисления проводятся с данными сечения спектральной плотности изображения, проведенного в выбранном направлении, Это позволяет охарактеризовать вытянутость формы КТ в определенном направлении. Для изображения, приведенного на рис. 8, таким образом полу-

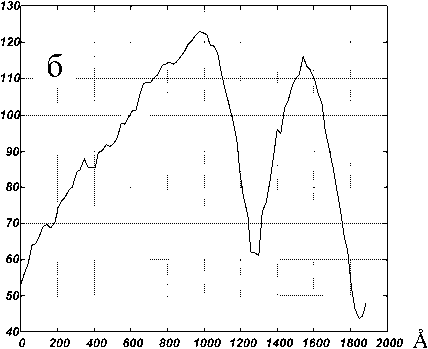
Рис. 10. а. СТМ-изображение ансамбля квантовых точек, площадь сканирования 6000 х 6000 А. б. Поперечное сечение изображения

чено по вертикальному сечению значение R_eepm = 120 ± 30 А, а по горизонтальному сечению — R_ropu3 = 82 ± 26А . Значения величин второго характерного размера по горизонтальному и вертикальному сечениям приблизительно совпадают и соответствуют результату, полученному для усредненного сечения, который приведен выше.

Для изображения, приведенного на рис. 10, результатом вычислений по горизонтальному сечению является двухмодовая плотность распределения радиусов КТ ( R 1 = 176 ± 50 А, R ₂ = 550 ± 40 А) (рис. 11).

На основании данных усредненного по направлениям сечения для изображения поверхности рис. 10 автоматически получено, что на нем находятся КТ со средним радиусом 250 ангстрем, а средняя плотность КТ на поверхности образца составляет 220 мкм ^-2 .

ВЫВОДЫ

Предложенный алгоритм определения плотности распределения размеров элементов цифрового полутонового изображения с помощью вычисления его спектральной плотности является работоспособным. Возможности алгоритма проверены на смоделированных изображениях. Проведено исследование изображений полупроводниковых гетероструктур, содержащих квантовые точки, и получены плотности распределения радиусов квантовых точек, средний радиус, разброс радиусов, средняя плотность, с которой КТ расположены на поверхности.

Работа выполнена при поддержке ГНТП «Физика твердотельных наноструктур» (Проект № 983010) и ФЦП «Интеграция» (Проект А 147).

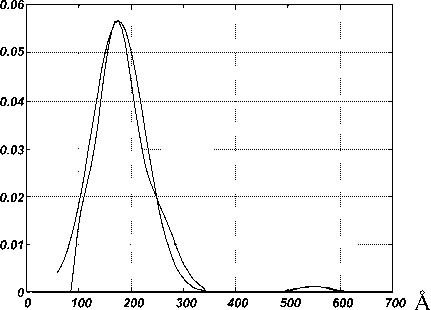
Рис. 11. Плотность распределения радиусов для ансамбля КТ, изображенного на рис. 10, вычисленная вдоль горизонтального сечения;

R 1 =176±50 Å, R 2 =550±30Å