Определение энергии виртуального pp-состояния в реакции d+1H -> p + p + n

Исследование и сравнение пп- и рр-взаимодействий являются важными в связи с проверкой гипотезы о зарядовой симметрии ядериых сил. Нарушение зарядовой симметрии ядериых сил, т.е. различие ядериых пп- и рр-взаимодействий, проявляется, в частности, в различии низкоэнергетических характеристик пп- и рр-взаимодействий - синглетных длин рассеяния и энергий виртуального ¹S'o уровня. Длина протон-протонного рассеяния была. определена, с высокой точностью из экспериментов по прямому рассеянию протона, на. протоне, и ее современное значение а_рр = -7.8149 ± 0.0029 фм приведено в [1].

Это экспериментальное значение включает вклад кулоновского взаимодействия. Однако основной интерес с точки зрения зарядовой симметрии представляет так называемая ядерная длина, протон-протонного рассеяния, которая не включает в себя кулоновский вклад. Если удалить кулоновское рр-взаимодействие, то полученное значение a_pp^N = 17.3± ±0.4 фм принимается в настоящее время как ядерная часть длины рр-рассеяния [2].

• (с) Копобеевский Е. С., Зуев C.B., Мордовской M.B., Афонин А. А., Каспаров А. А., Мицук В. В., 2019

2.    Моделирование реакции d +1 Н —> (р + р) + п

«Московский физико-технический институт (национальный исследовательский университет)», 2019

Нейтрон-нейтронная длина рассеяния определяется в основном в реакциях п + d —> р + п + п и тг^- + d —> 7 + п + п при исследовании взаимодействия в конечном состоянии двух нейтронов, имеющих малую относительную энергию. В [3] было высказано предположение, что разброс значений а_пп (от -16 до -22 Фм), полученный в реакциях с тремя частицами в конечном состоянии, может быть связан со значительным влиянием З-У-сил. Можно предположить, что и значения протон-протонной длины рассеяния а_рр и энергии виртуального ¹ So уровня Е_рр, извлеченные из экспериментов с тремя или четырьмя частицами в конечном состоянии, будут отличаться от значений, полученных в свободном рр-рассеянии. Для проверки этого предположения в ИЯИ РАН запланированы работы по исследованию реакций d +1 Н —> р + р + п, d +2 Н —> р + р + п + п и р +2 Н —> р + р + п. Во всех этих реакциях в промежуточном состоянии возможно взаимодействие рр-пары с нейтроном (или пп-парой), что может отразиться на величинах извлекаемых низкоэнергетических параметров ( а_рр и Ерр). В настоящей работе приводятся результаты подготовки эксперимента по извлечению величины Е_рр в реакциях d +1 Н —> р + р + п и d +2 Н —> р + р + п + п - результаты кинематического моделирования реакций, а также схема установки для проведения эксперимента.

Моделирование планируемых экспериментов проводилось с помощью программ, предназначенных для изучения реакций с тремя и более частицами в конечном состоянии и идущих в два этапа через распадающиеся промежуточные состояния [4,5]. Планируемые эксперименты будут проведены совместно с НИИЯФ МГУ им. Д.В. Скобельцына на пучке дейтронов ускорителя У-120 при энергии 15 МэВ. Рассмотрим моделирование реакции d +1 Н —> (р + р) + п —> р + р + п, проходящей через стадию образования виртуального спиглетпого рр-состояния.

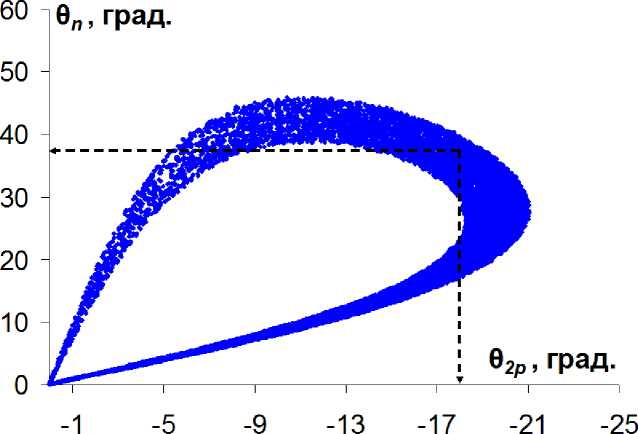
Рис. 1. Результаты моделирования реакции d +1 Н —у (р + р) + п: двумерная диаграмма Ө_2р — Ө_п. Стрелками отмечены выбранные углы вылета, нейтрона, и двухпротонной системы

Задача эксперимента состоит в определении энергии виртуального синглетного рр-состояния в реакции с тремя частицами в конечном состоянии. Моделирование реакции проведено в два этапа. На первом этапе моделируется двухчастичная реакция d+1 Н —> (р+р)+п. Затравочная масса двухпротонной системы имеет вид т_2р = 2т_р+Е_рр. В работе [6] в четырехчастичной реакции d +2 Н —> р + р + п + п получено значение Е_рр = 0.43±0.09 МэВ. Экспериментальное значение длины протон-протонного рассеяния а_рр = -7.8149±0.0029 фм, приведенное в работе [7], соответствует значению Е_рр =

= 0.51 МэВ. Поскольку искомое значение энергии виртуального уровня в рассматриваемой реакции неизвестно, при моделировании оно бралось в широком интервале Е_рр = = 0.5±0.3 МэВ. В результате моделирования были получены двумерные диаграммы «угол-угол» (рис. 1) и «энергия-энергия» (рис. 2) для фрагментов (р + р) и п.

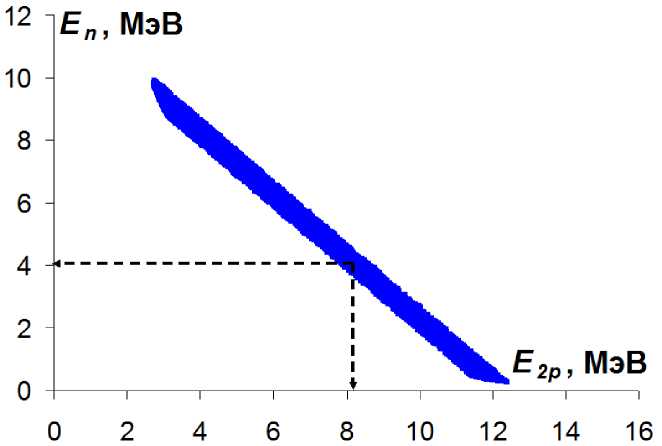
Рис. 2. Результаты моделирования реакции d +1 Н —> (р + р) + п двумерная диаграмма Е2_р-Е_Т. Стрелками отмечены кинетические энергии нейтрона, и двухпротонной системы, соответствующие их углам вылета.

Учитывая экспериментальные условия (угол установки детектора, заряженных частиц должен быть не менее 15°), были определены оптимальные углы вылета нейтрона и рр- системы: Ө2_Р = -18° ± 1.5°, Ө_п = 38° ± 2°, соответствующие максимально возможным в эксперименте энергиям протонов. Положительным и отрицательным углам соответствуют углы вылета, налево и направо от оси пучка, соответственно. На втором этапе моделируется реакция трехчастичного развала d +1 Н —> р+р+п. В эксперименте будут регистрироваться в совпадении один из протонов и нейтрон под углами, близкими к углам вылета двухпротонной системы и нейтрона, в двухчастичной реакции. Для каждого моделированного события относительная энергия системы двух протонов, т.е. превышение полной энергии рр-системы над ее массой, рассчитывается по формуле [8]:

^Е = 2^(Ер1 ^{+ Е}р2 ^{— 2}V^ЕP1^Ер2^COs(ӨP1 - ^2))

через кинетические энергии протонов и угол их разлета (разница углов вылета Өрі и Өр2) в лабораторной системе. При этом, для всех событий (синие точки на. диаграмме рис. 3) два протона могут иметь относительную энергию Е в интервале от 0 до 1.4 МэВ.

На рис. 3 показана двумерная диаграмма Е_р — Е_п для всех событий развала d +1 Н. Отбор событий со значениями относительной энергии рр-системы е в интервале Е_рр ±Г приводит к структуре как в двумерных диаграммах, так и в энергетическом спектре протонов (рис. 4).

Наличие двух пиков в энергетическом спектре протонов (рис. 4) объясняется тем, что в реакциях с образованием и развалом виртуального УУ-состояния при условии детектирования «развальной» частицы под углом, близким к углу вылета УУ-системы, попасть в детектор могут только частицы от развала УУ-состояния, вылетающие в системе ц.м. или вперед (0°) или назад (180°). При этом разность между энергиями в спектре зависит от энергии виртуального УУ-состояния. Энергетические спектры протонов (рис. 4), образующиеся в реакции d +1 Н —> р + р + п, получены проецированием областей диаграммы (соответствующих различным значениям Ерр) из рис. 3 на ось ординат, после поворота осей на угол 20° по часовой стрелке. Отметим, что энергия вылетающих протонов в этом случае достаточно велика, и детекторы для регистрации заряженных частиц можно установить вне вакуумной камеры.

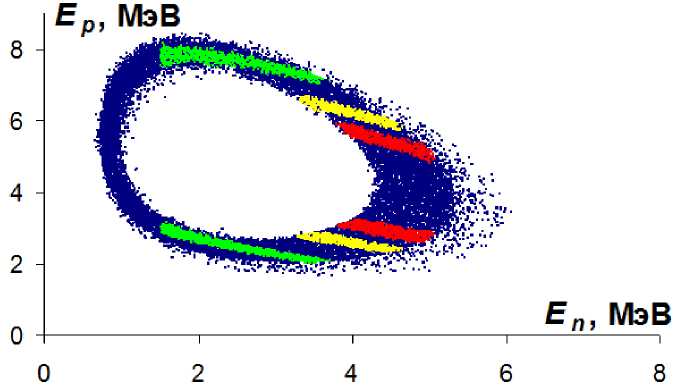
Рис. 3. Результаты моделирования реакции d +1 Н —> р + р +п: энергетическая зависимость Е_р-Е_Т. Параметры моделирования: Ед = 15 МэВ, Ө _{2 р} = -18° ± 1.5°, Ө_Т = 38° ± 2°. Цветом выделены события, соответствующие различным значениям е: синим цветом - всем значениям е, красным -значениям е в днапазоне 200±50 кэВ. желтым - 400±50 кэВ. зеленым - 800±50 кэВ

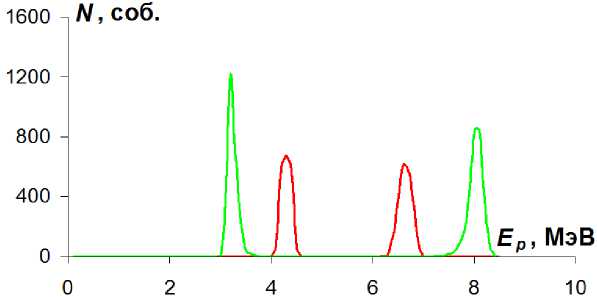
Рис. 4. Энергетические спектры протонов, образующиеся в реакции d +1 Н —> р + р + п для различных значений е: 200±50 кэВ (красный цвет) и 800±50 кэВ (зеленый цвет)

На рис. 4 показано, что при увеличении значения Е_рр увеличивается расстояние между пиками в энергетическом спектре протонов. Следовательно, анализируя полученный в эксперименте энергетический спектр протонов, можно определить с достаточной точностью значение величины энергии Е_рр виртуального синглетного рр-состояния. Полученные в результате моделирования трехчастичной реакции d +1 Н —> р + р + п данные об энергиях протонов были использованы для вычисления ионизационных потерь в кремниевых АЕ- и Е-детекторах (толщины детекторов составляют 25 и 1000 мкм соответственно). На рис. 5 показана АЕ — Е-диаграмма ионизационных потерь протонов с энергиями от 1 до 15 МэВ и с энергиями, соответствующими е = 700±50 кэВ. Как показало моделирование, наличие двух пиков в энергетическом спектре протонов после прохождения АЕ — Е системы сохраняется.

Кинематическое моделирование показало, что при определенных кинематических условиях имеется прямая зависимость формы энергетического распределения «развальной» частицы от энергии квазисвязанного состояния, позволяющая определить эту важную ха- рактеристику нуклон-нуклонного взаимодействия. В ходе моделирования был установлен доступный для исследования диапазон Ерр (200-800 кэВ).

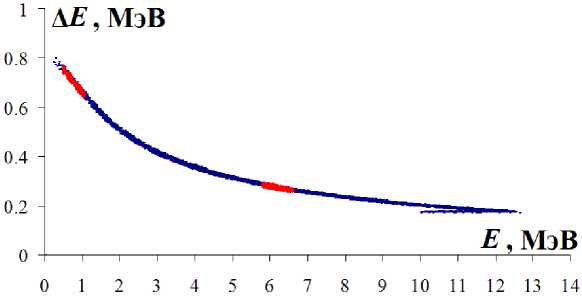
Рис. 5. ДЕ — Е-диаграмма ионизационных потерь протонов для детекторов с толщинами 25 и 1000 мкм соответственно. Синие точки соответствуют ионизационным потерям протонов с энергиями от 1 до 15 МэВ, красные точки - спектру протонов для е = 700±50 кэВ

• 3.    Моделирование реакции d +2 Н —>(р + р) + (п + п) —>р + р + п + п

4.    Экспериментальная установка для исследования реакций d +1 Н —> (р + р) + п и d +2 Н —> (р + р) + (п + п) 5.    Заключение

Было проведено также моделирование реакции d+‘2Н —> (р+р) + (п+п) —> р+р+п+п, которая может проходить с образованием на первом этапе синглетных двухпротонной и двухнейтронной систем. Задача этого эксперимента состоит в определении энергии виртуального синглетного рр-состояния в реакции с четырьмя частицами в конечном состоянии. В эксперименте предполагается регистрация в совпадении двух протонов и нейтрона от развала двухнуклонных систем. Кинематическое моделирование данной реакции при энергии дейтронов 15 МэВ также проводилось в два этапа. На первом выбираются оптимальные углы вылета двухнуклонных систем: Ө2_р = -22°±2° и Ө2,, = 34°±2° в реакции d+2 Н —> (р +р) + (п + п). На втором этапе моделируется реакция с четырьмя частицами в конечном состоянии d+² Н —> р+р +п+п, при этом расположение детектора нейтронов соответствует углу вылета двухнейтронной системы, а для двух протонов соответствующие углы вылета составляют -21.8° и -23.2°, что обусловлено геометрией детектора протонов. Регистрация протонов будет осуществляться с помощью детектора на основе матрицы Si ФЭУ фирмы SENSL и кристаллов LFS-8. Подробно характеристики этого детектора и методика работы с данной матрицей описаны в работах [9, 10]. Как показали результаты моделирования, отбор событий со значениями энергии рр-системы Е_рр в интервале ±Г(Е_рр-Г; Е_рр + Г) также приводит к структуре с двумя пиками в энергетическом спектре протонов. Дальнейшее моделирование ионизационных потерь протонов в Е-детекторе для различных значений Е_рр показало, что для реакции d +2 Н —> р + р + п + п возможен эксперимент с определением Е_рр в диапазоне 200-750 кэВ. Исследование реакций d +1 Н —> (р +р) + пи d +2 Н —> (р + р) + (п + п) позволит исследовать влияние фрагмента (нейтрона или пп-пары) на величину извлекаемой энергии виртуального рр-состояния в реакциях с тремя и четырьмя частицами в конечном состоянии.

Для проведения данных исследований планируется использовать дейтронный пучок ускорителя У-120 НИИЯФ МГУ им. Д.В. Скобельцына с энергией 15 МэВ. Пучок дейтронов облучает водородосодержащую (или дейтерированную) мишень, помещенную в вакуумную камеру диаметром 23 см с выходным окном из лавсана толщиной 20 мкм. Наличие тонкого выходного окна позволяет устанавливать детекторы заряженных частиц снаружи камеры. Исходя из результатов моделирования, была спроектирована и создана экспериментальная установка (рис. 6) для изучения реакции d+1 Н —> р+р+п. Для исследования реакции d +2 Н —> р + р + п + п кремниевый S-детектор будет заменен на систему 8ІФЭУ, и вся AS — S-система будет внесена внутрь камеры.

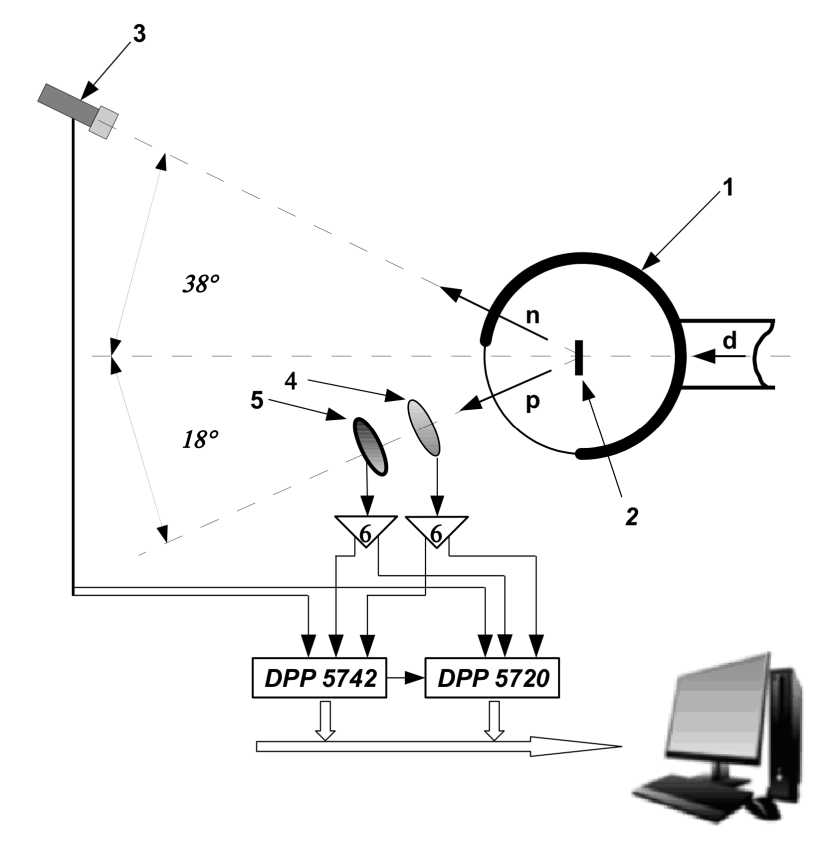
Рис. 6. Схема экспериментальной установки для регистрации заряженных частиц и нейтронов:

1 - вакуумная камера рассеяния, 2 - мишень CH2, 3 - детектор нейтронов, 4 - кремниевый тонкий AS-детектор (25 мкм), 5 - S-детектор или система детекторов (выбирается в соответствии с используемой экспериментальной схемой), 6 - система, включающая в себя предусилитель и усилитель каждого детектора, DPP 5742 и DPP 5720 - цифровые сигнальные процессоры

Установка (рис. 6) содержит два плеча регистрации частиц. Для измерения энергии и определения типа заряженной частицы используется телескоп кремниевых AS-S детекторов. Сигналы с детекторов подаются через соответствующие тракты усиления на цифровые сигнальные процессоры (ЦСП) CAEN DT5720 и DT5742 (выбор ЦСП для эксперимента зависит от конкретной реализации и необходимости регистрировать временной сигнал от того или иного детектора установки). В случае исследования реакции d +² Н —> р + р + п + п S- и AS-детекторы вносятся внутрь камеры рассеяния, так как энергии протонов малы и недостаточны для прохождения пленки из лавсана и слоя воздуха до детектирующей системы. Второе плечо регистрации содержит жидкий водородсодержащий сцинтилляционный детектор нейтронов EJ-301. Энергия нейтронов определяется по времени пролета до детектора. В качестве стартового сигнала времяпролетной системы используется быстрый сигнал предусилителя S-детектора заряженных частиц телескопа. ЦСП DT5720 используется для оцифровки медленных (амплитудных) сигналов, а ЦСП DT5742, имеющий шаг оцифровки 0.2 нс, — для оцифровки быстрых. Через буферную память ЦСП оцифрованные сигналы передаются в основной компьютер. Обработка информации ведется в режиме off-line. Она заключается в определении амплитуд и площадей импульсов, определении времен возникновения сигналов в детекторах, цифровом анализе формы импульсов для п — у разделения, отборе совпадающих событий и получении энергетических и временных спектров.

Рассмотрена возможность исследования реакций d +1 Н —> р + р + п и d +1 Н —> р + р + п + п с целью измерения энергии виртуального синглетного рр-состояния в реакциях с тремя и четырьмя частицами в конечном состоянии. Идея предлагаемых экспериментов состоит в том, что в результате измерения энергетических спектров протонов можно определить величину энергии виртуального рр-состояния в случаях возможного влияния нейтрона или пп-пары на извлекаемую величину. Кинематическое моделирование реакций с образованием и развалом квазисвязанного рр-состояния показало, что при определенных кинематических условиях имеется прямая зависимость формы энергетического распределения «развальной» частицы от энергии квазисвязанного состояния, позволяющая определить эту важную характеристику нуклон-нуклонного взаимодействия. В ходе моделирования реакций был установлен доступный для исследования диапазон Е_рр (200800 кэВ для d +1 Н —> р + р + п и 200-750 кэВ для d+2 Н —> р + р + п +п). Установлено, что для первой реакции энергия вылетающих частиц достаточно велика для установки детекторов заряженных частиц вне вакуумной камеры. Создана экспериментальная установка для изучения данной реакции, начаты тестовые измерения.